Growth of Accreting Supermassive Black Hole Seeds and Neutrino Radiation
Abstract
In the framework of microscopic theory of black hole (MTBH), which explores the most important processes of rearrangement of vacuum state and spontaneous breaking of gravitation gauge symmetry at huge energies, we have undertaken a large series of numerical simulations with the goal to trace an evolution of the mass assembly history of 377 plausible accreting supermassive black hole seeds in active galactic nuclei (AGNs) to the present time and examine the observable signatures today. Given the redshifts, masses, and luminosities of these black holes at present time collected from the literature, we compute the initial redshifts and masses of the corresponding seed black holes. For the present masses MBH/M⊙≃1.1 × 106 to 1.3 × 1010 of 377 black holes, the computed intermediate seed masses are ranging from to 2.9 × 105. We also compute the fluxes of ultrahigh energy (UHE) neutrinos produced via simple or modified URCA processes in superdense protomatter nuclei. The AGNs are favored as promising pure UHE neutrino sources, because the computed neutrino fluxes are highly beamed along the plane of accretion disk, peaked at high energies, and collimated in smaller opening angle (θ ≪ 1).
1. Introduction
With typical bolometric luminosities ~1045−48 erg s−1, the AGNs are amongst the most luminous emitters in the universe, particularly at high energies (gamma-rays) and radio wavelengths. From its historical development, up to current interests, the efforts in the AGN physics have evoked the study of a major unsolved problem of how efficiently such huge energies observed can be generated. This energy scale severely challenges conventional source models. The huge energy release from compact regions of AGN requires extremely high efficiency (typically ≥10 per cent) of conversion of rest mass to other forms of energy. This serves as the main argument in favour of supermassive black holes, with masses of millions to billions of times the mass of the Sun, as central engines of massive AGNs. The astrophysical black holes come in a wide range of masses, from ≥3M⊙ for stellar mass black holes [1] to ~1010M⊙ for supermassive black holes [2, 3]. Demography of local galaxies suggests that most galaxies harbour quiescent supermassive black holes in their nuclei at the present time and that the mass of the hosted black hole is correlated with properties of the host bulge. The visible universe should therefore contain at least 100 billion supermassive black holes. A complex study of evolution of AGNs requires an answer to the key questions such as how did the first black holes form, how did massive black holes get to the galaxy centers, and how did they grow in accreting mass, namely, an understanding of the important phenomenon of mass assembly history of accreting supermassive black hole seeds. The observations support the idea that black holes grow in tandem with their hosts throughout cosmic history, starting from the earliest times. While the exact mechanism for the formation of the first black holes is not currently known, there are several prevailing theories [4]. However, each proposal towards formation and growth of initial seed black holes has its own advantage and limitations in proving the whole view of the issue. In this report we review the mass assembly history of 377 plausible accreting supermassive black hole seeds in AGNs and their neutrino radiation in the framework of gravitation theory, which explores the most important processes of rearrangement of vacuum state and a spontaneous breaking of gravitation gauge symmetry at huge energies. We will proceed according to the following structure. Most observational, theoretical, and computational aspects of the growth of black hole seeds are summarized in Section 2. The other important phenomenon of ultrahigh energy cosmic rays, in relevance to AGNs, is discussed in Section 3. The objectives of suggested approach are outlined in Section 4. In Section 5 we review the spherical accretion on superdense protomatter nuclei, in use. In Section 6 we discuss the growth of the seed black hole at accretion and derive its intermediate mass, initial redshift, and neutrino preradiation time (PRT). Section 7 is devoted to the neutrino radiation produced in superdense protomatter nuclei. The simulation results of the seed black hole intermediate masses, PRTs, seed redshifts, and neutrino fluxes for 377 AGN black holes are brought in Section 8. The concluding remarks are given in Section 9. We will refrain from providing lengthy details of the proposed gravitation theory at huge energies and neutrino flux computations. For these the reader is invited to visit the original papers and appendices of the present paper. In the latter we also complete the spacetime deformation theory, in the model context of gravitation, by new investigation of building up the complex of distortion (DC) of spacetime continuum and showing how it restores the world-deformation tensor, which still has been put in by hand. Finally, note that we regard the considered black holes only as the potential neutrino sources. The obtained results, however, may suffer if not all live black holes at present reside in final stage of their growth driven by the formation of protomatter disk at accretion and they radiate neutrino. We often suppress the indices without notice. Unless otherwise stated, we take geometrized units throughout this paper.
2. A Breakthrough in Observational and Computational Aspects on Growth of Black Hole Seeds
Significant progress has been made in the last few years in understanding how supermassive black holes form and grow. Given the current masses of 106−9M⊙, most black hole growth happens in the AGN phase. A significant fraction of the total black hole growth, 60% [6], happens in the most luminous AGN, quasars. In an AGN phase, which lasts ~108 years, the central supermassive black hole can gain up to ~107−8M⊙, so even the most massive galaxies will have only a few of these events over their lifetime. Aforesaid gathers support especially from a breakthrough made in recent observational, theoretical, and computational efforts in understanding of evolution of black holes and their host galaxies, particularly through self-regulated growth and feedback from accretion-powered outflows; see, for example, [4, 7–18]. Whereas the multiwavelength methods are used to trace the growth of seed BHs, the prospects for future observations are reviewed. The observations provide strong support for the existence of a correlation between supermassive black holes and their hosts out to the highest redshifts. The observations of the quasar luminosity function show that the most supermassive black holes get most of their mass at high redshift, while at low redshift only low mass black holes are still growing [19]. This is observed in both optical [20] and hard X-ray luminosity functions [19, 21], which indicates that this result is independent of obscuration. Natarajan [13] has reported that the initial black hole seeds form at extremely high redshifts from the direct collapse of pregalactic gas discs. Populating dark matter halos with seeds formed in this fashion and using a Monte-Carlo merger tree approach, he has predicted the black hole mass function at high redshifts and at the present time. The most aspects of the models that describe the growth and accretion history of supermassive black holes and evolution of this scenario have been presented in detail by [9, 10]. In these models, at early times the properties of the assembling black hole seeds are more tightly coupled to properties of the dark matter halo as their growth is driven by the merger history of halos. While a clear picture of the history of black hole growth is emerging, significant uncertainties still remain [14], and in spite of recent advances [6, 13], the origin of the seed black holes remains an unsolved problem at present. The NuSTAR deep high-energy observations will enable obtaining a nearly complete AGN survey, including heavily obscured Compton-thick sources, up to z ~ 1.5 [22]. A similar mission, ASTRO-H [23], will be launched by Japan in 2014. These observations in combination with observations at longer wavelengths will allow for the detection and identification of most growing supermassive black holes at z ~ 1. The ultradeep X-ray and near-infrared surveys covering at least ~1 deg2 are required to constrain the formation of the first black hole seeds. This will likely require the use of the next generation of space-based observatories such as the James Webb Space Telescope and the International X-ray Observatory. The superb spatial resolution and sensitivity of the Atacama Large Millimeter Array (ALMA) [24] will revolutionize our understanding of galaxy evolution. Combining these new data with existing multiwavelength information will finally allow astrophysicists to pave the way for later efforts by pioneering some of the census of supermassive black hole growth, in use today.
3. UHE Cosmic-Ray Particles
The galactic sources like supernova remnants (SNRs) or microquasars are thought to accelerate particles at least up to energies of 3 × 1015 eV. The ultrahigh energy cosmic-ray (UHECR) particles with even higher energies have since been detected (comprehensive reviews can be found in [25–29]). The accelerated protons or heavier nuclei up to energies exceeding 1020 eV are firstly observed by [30]. The cosmic-ray events with the highest energies so far detected have energies of 2 × 1011 GeV [31] and 3 × 1011 GeV [32]. These energies are 107 times higher than the most energetic man-made accelerator, the LHC at CERN. These highest energies are believed to be reached in extragalactic sources like AGNs or gamma-ray bursts (GRBs). During propagation of such energetic particles through the universe, the threshold for pion photoproduction on the microwave background is ~2 × 1010 GeV, and at ~3 × 1011 GeV the energy-loss distance is about 20 Mpc. Propagation of cosmic rays over substantially larger distances gives rise to a cutoff in the spectrum at ~1011 GeV as was first shown by [33, 34], the GZK cutoff. The recent confirmation [35, 36] of GZK suppression in the cosmic-ray energy spectrum indicates that the cosmic rays with energies above the GZK cutoff, EGZK ~ 40 EeV, mostly come from relatively close (within the GZK radius, rGZK ~ 100 Mpc) extragalactic sources. However, despite the detailed measurements of the cosmic-ray spectrum, the identification of the sources of the cosmic-ray particles is still an open question as they are deflected in the galactic and extragalactic magnetic fields and hence have lost all information about their origin when reaching Earth. Only at the highest energies beyond ~1019.6 GeV cosmic-ray particles may retain enough directional information to locate their sources. The latter must be powerful enough to sustain the energy density in extragalactic cosmic rays of about 3 × 10−19 erg cm−3 which is equivalent to ~8 × 1044 erg Mpc−3 yr−1. Though it has not been possible up to now to identify the sources of galactic or extragalactic cosmic rays, general considerations allow limiting potential source classes. For example, the existing data on the cosmic-ray spectrum and on the isotropic 100 MeV gamma-ray background limit significantly the parameter space in which topological defects can generate the flux of the highest energy cosmic rays and rule out models with the standard X-particle mass of 1016 GeV and higher [37]. Eventually, the neutrinos will serve as unique astronomical messengers, and they will significantly enhance and extend our knowledge on galactic and extragalactic sources of the UHE universe. Indeed, except for oscillations induced by transit in a vacuum Higgs field, neutrinos can penetrate cosmological distances and their trajectories are not deflected by magnetic fields as they are neutral, providing powerful probes of high energy astrophysics in ways which no other particle can. Moreover, the flavor composition of neutrinos originating at astrophysical sources can serve as a probe of new physics in the electroweak sector. Therefore, an appealing possibility among the various hypotheses of the origin of UHECR is so-called Z-burst scenario [38–51]. This suggests that if ZeV astrophysical neutrino beam is sufficiently strong, it can produce a large fraction of observed UHECR particles within 100 Mpc by hitting local light relic neutrinos clustered in dark halos and form UHECR through the hadronic Z (s-channel production) and W-bosons (t-channel production) decays by weak interactions. The discovery of UHE neutrino sources would also clarify the production mechanism of the GeV-TeV gamma rays observed on Earth [43, 52, 53] as TeV photons are also produced in the up-scattering of photons in reactions to accelerated electrons (inverse-Compton scattering). The direct link between TeV gamma-ray photons and neutrinos through the charged and neutral pion production, which is well known from particle physics, allows for a quite robust prediction of the expected neutrino fluxes provided that the sources are transparent and the observed gamma rays originate from pion decay. The weakest link in the Z-burst hypothesis is probably both unknown boosting mechanism of the primary neutrinos up to huge energies of hundreds ZeV and their large flux required at the resonant energy well above the GZK cutoff. Such a flux severely challenges conventional source models. Any concomitant photon flux should not violate existing upper limits [37, 48, 49, 54]. The obvious question is then raised: where in the Cosmos are these neutrinos coming from? It turns out that currently, at energies in excess of 1019 eV, there are only two good candidate source classes for UHE neutrinos: AGNs and GRBs. The AGNs as significant point sources of neutrinos were analyzed in [50, 55, 56]. While hard to detect, neutrinos have the advantage of representing aforesaid unique fingerprints of hadron interactions and, therefore, of the sources of cosmic rays. Two basic event topologies can be distinguished: track-like patterns of detected Cherenkov light (hits) which originate from muons produced in charged-current interactions of muon neutrinos (muon channel); spherical hit patterns which originate from the hadronic cascade at the vertex of neutrino interactions or the electromagnetic cascade of electrons from charged-current interactions of electron neutrinos (cascade channel). If the charged-current interaction happens inside the detector or in case of charged-current tau-neutrino interactions, these two topologies overlap which complicates the reconstruction. At the relevant energies, the neutrino is approximately collinear with the muon and, hence, the muon channel is the prime channel for the search for point-like sources of cosmic neutrinos. On the other hand, cascades deposit all of their energy inside the detector and therefore allow for a much better energy reconstruction with a resolution of a few 10%. Finally, numerous reports are available at present in literature on expected discovery potential and sensitivity of experiments to neutrino point-like sources. Currently operating high energy neutrino telescopes attempt to detect UHE neutrinos, such as ANTARES [57, 58] which is the most sensitive neutrino telescope in the Northern Hemisphere, IceCube [35, 59–64] which is worldwide largest and hence most sensitive neutrino telescope in the Southern Hemisphere, BAIKAL [65], as well as the CR extended experiments of The Telescope Array [66], Pierre Auger Observatory [67, 68], and JEM-EUSO mission [69]. The JEM-EUSO mission, which is planned to be launched by a H2B rocket around 2015-2016, is designed to explore the extremes in the universe and fundamental physics through the detection of the extreme energy (E > 1020 eV) cosmic rays. The possible origins of the soon-to-be famous 28 IceCube neutrino-PeV events [59–61] are the first hint for astrophysical neutrino signal. Aartsen et al. have published an observation of two ~1 PeV neutrinos, with a P value 2.8σ beyond the hypothesis that these events were atmospherically generated [59]. The analysis revealed an additional 26 neutrino candidates depositing “electromagnetic equivalent energies” ranging from about 30 TeV up to 250 TeV [61]. New results were presented at the IceCube Particle Astrophysics Symposium (IPA 2013) [62–64]. If cosmic neutrinos are primarily of extragalactic origin, then the 100 GeV gamma ray flux observed by Fermi-LAT constrains the normalization at PeV energies at injection, which in turn demands a neutrino spectral index Γ < 2.1 [70].
4. MTBH, Revisited: Preliminaries
For the benefit of the reader, a brief outline of the key ideas behind the microscopic theory of black hole, as a guiding principle, is given in this section to make the rest of the paper understandable. There is a general belief reinforced by statements in textbooks that, according to general relativity (GR), a long-standing standard phenomenological black hole model (PBHM)—namely, the most general Kerr-Newman black hole model, with parameters of mass (M), angular momentum (J), and charge (Q), still has to be put in by hand—can describe the growth of accreting supermassive black hole seed. However, such beliefs are suspect and should be critically reexamined. The PBHM cannot be currently accepted as convincing model for addressing the aforementioned problems, because in this framework the very source of gravitational field of the black hole is a kind of curvature singularity at the center of the stationary black hole. A meaningless central singularity develops which is hidden behind the event horizon. The theory breaks down inside the event horizon which is causally disconnected from the exterior world. Either the Kruskal continuation of the Schwarzschild (J = 0, Q = 0) metric, or the Kerr (Q = 0) metric, or the Reissner-Nordstrom (J = 0) metric, shows that the static observers fail to exist inside the horizon. Any object that collapses to form a black hole will go on to collapse to a singularity inside the black hole. Thereby any timelike worldline must strike the central singularity which wholly absorbs the infalling matter. Therefore, the ultimate fate of collapsing matter once it has crossed the black hole surface is unknown. This, in turn, disables any accumulation of matter in the central part and, thus, neither the growth of black holes nor the increase of their mass-energy density could occur at accretion of outside matter, or by means of merger processes. As a consequence, the mass and angular momentum of black holes will not change over the lifetime of the universe. But how can one be sure that some hitherto unknown source of pressure does not become important at huge energies and halt the collapse? To fill the void which the standard PBHM presents, one plausible idea to innovate the solution to alluded key problems would appear to be the framework of microscopic theory of black hole. This theory has been originally proposed by [71] and references therein and thoroughly discussed in [72–75]. Here we recount some of the highlights of the MTBH, which is the extension of PBHM and rather completes it by exploring the most important processes of rearrangement of vacuum state and a spontaneous breaking of gravitation gauge symmetry at huge energies [71, 74, 76]. We will not be concerned with the actual details of this framework but only use it as a backdrop to validate the theory with some observational tests. For details, the interested reader is invited to consult the original papers. Discussed gravitational theory is consistent with GR up to the limit of neutron stars. But this theory manifests its virtues applied to the physics of internal structure of galactic nuclei. In the latter a significant change of properties of spacetime continuum, so-called inner distortion (ID), arises simultaneously with the strong gravity at huge energies (see Appendix A). Consequently the matter undergoes phase transition of second kind, which supplies a powerful pathway to form a stable superdense protomatter core (SPC) inside the event horizon. Due to this, the stable equilibrium holds in outward layers too and, thus, an accumulation of matter is allowed now around the SPC. The black hole models presented in phenomenological and microscopic frameworks have been schematically plotted in Figure 1, to guide the eye. A crucial point of the MTBH is that a central singularity cannot occur, which is now replaced by finite though unbelievably extreme conditions held in the SPC, where the static observers existed. The SPC surrounded by the accretion disk presents the microscopic model of AGN. The SPC accommodates the highest energy scale up to hundreds of ZeV in central protomatter core which accounts for the spectral distribution of the resulting radiation of galactic nuclei. External physics of accretion onto the black hole in earlier part of its lifetime is identical to the processes in Schwarzschild’s model. However, a strong difference in the model context between the phenomenological black hole and the SPC is arising in the second part of its lifetime (see Section 6). The seed black hole might grow up driven by the accretion of outside matter when it was getting most of its mass. An infalling matter with time forms the protomatter disk around the protomatter core tapering off faster at reaching out the thin edge of the event horizon. At this, metric singularity inevitably disappears (see appendices) and the neutrinos may escape through vista to outside world, even after the neutrino trapping. We study the growth of protomatter disk and derive the intermediate mass and initial redshift of seed black hole and examine luminosities, neutrino surfaces for the disk. In this framework, we have computed the fluxes of UHE neutrinos [75], produced in the medium of the SPC via simple (quark and pionic reactions) or modified URCA processes, even after the neutrino trapping (G. Gamow was inspired to name the process URCA after the name of a casino in Rio de Janeiro, when M. Schenberg remarked to him that “the energy disappears in the nucleus of the supernova as quickly as the money disappeared at that roulette table”). The “trapping” is due to the fact that as the neutrinos are formed in protomatter core at superhigh densities they experience greater difficulty escaping from the protomatter core before being dragged along with the matter; namely, the neutrinos are “trapped” comove with matter. The part of neutrinos annihilates to produce, further, the secondary particles of expected ultrahigh energies. In this model, of course, a key open question is to enlighten the mechanisms that trigger the activity, and how a large amount of matter can be steadily funneled to the central regions to fuel this activity. In high luminosity AGNs the large-scale internal gravitational instabilities drive gas towards the nucleus which trigger big starbursts, and the coeval compact cluster just formed. It seemed they have some connection to the nuclear fueling through mass loss of young stars as well as their tidal disruption and supernovae. Note that we regard the UHECR particles as a signature of existence of superdence protomatter sources in the universe. Since neutrino events are expected to be of sufficient intensity, our estimates can be used to guide investigations of neutrino detectors for the distant future.

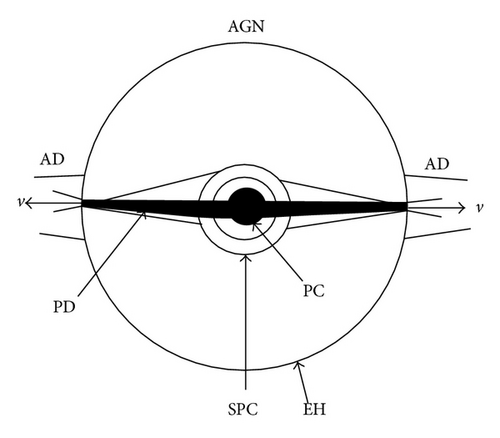
5. Spherical Accretion onto SPC
As alluded to above, the MTBH framework supports the idea of accreting supermassive black holes which link to AGNs. In order to compute the mass accretion rate , in use, it is necessary to study the accretion onto central supermassive SPC. The main features of spherical accretion can be briefly summed up in the following three idealized models that illustrate some of the associated physics [72].
5.1. Free Radial Infall
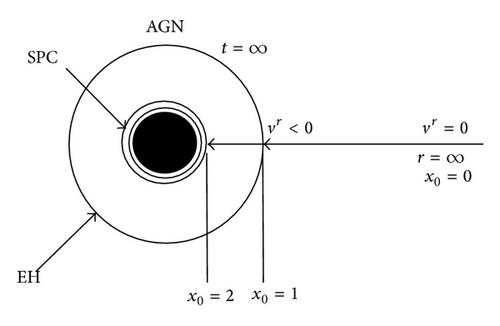
5.2. Collisionless Accretion
5.3. Hydrodynamic Accretion
6. The Intermediate Mass, PRT, and Initial Redshift of Seed Black Hole
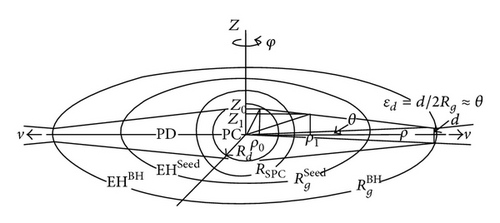
6.1. The Intermediate Mass of Seed Black Hole
6.2. PRT
6.3. Redshift of Seed Black Hole
7. UHE Neutrino Fluxes
7.1. URCA Reactions
7.2. Pionic Reactions
7.3. Quark Reactions
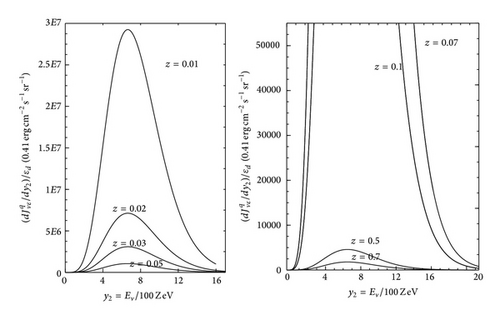
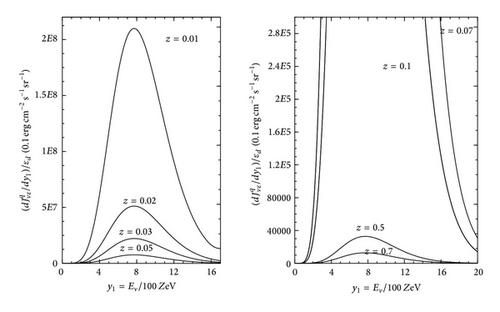
8. Simulation
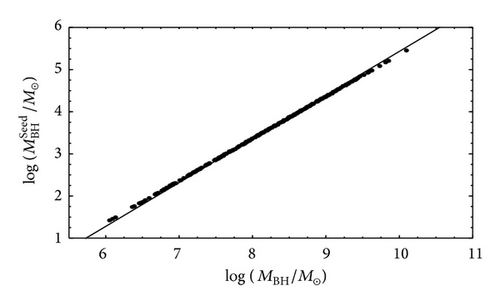
For simulation we use the data of AGN/BH mass and luminosity estimates for 377 black holes presented by [5]. These masses are mostly based on the virial assumption for the broad emission lines, with the broad-line region size determined from either reverberation mapping or optical luminosity. Additional black hole mass estimates based on properties of the host galaxy bulges, either using the observed stellar velocity dispersion or using the fundamental plane relation. Since the aim is to have more than a thousand of realizations, each individual run is simplified, with a use of previous algorithm of the SPC-configurations [71] as a working model, given in Appendix G. Computing the corresponding PRTs, seed black hole intermediate masses, and total neutrino fluxes, a main idea comes to solving an inverse problem. Namely, by the numerous reiterating integrations of the state equations of SPC-configurations we determine those required central values of particle concentration and ID-field x(0), for which the integrated total mass of configuration has to be equal to the black hole mass MBH given from observations. Along with all integral characteristics, the radius Rd is also computed, which is further used in (10), (14), (15), (18), (21), and (24) for calculating , TBH, zSeed, and , respectively. The results are summed up in Tables 1, 2, 3, 4 and 5. Figure 6 gives the intermediate seed masses versus the present masses MBH/M⊙ of 337 black holes, on logarithmic scales. For the present masses MBH/M⊙≃1.1 × 106 to 1.3 × 1010, the computed intermediate seed masses are ranging from . The computed neutrino fluxes are ranging from (1) (quark reactions)—, with the average ; (2) (pionic reactions)—, with the average ; and (3) (modified URCA processes)—, with the average . In accordance, the AGNs are favored as promising pure neutrino sources because the computed neutrino fluxes are highly beamed along the plane of accretion disk and peaked at high energies and collimated in smaller opening angle θ ~ εd = d/2 rg ≪ 1. To render our discussion here a bit more transparent and to obtain some feeling for the parameter εd we may estimate εd≃1.69 × 10−10, just for example, only, for the suppermassive black hole of typical mass ~109M⊙(2 Rg = 5.9 × 1014 cm), and so d ~ 1 km. But the key problem of fixing the parameter εd more accurately from experiment would be an important topic for another investigation elsewhere.
| Name | z | Type | logLbol |
|
|
|
logTBH | zSeed | Jq | JURCA | Jπ |
|---|---|---|---|---|---|---|---|---|---|---|---|
| NGC 1068 | 0.004 | SY2 | 44.98 | −7.59201 | 7.23 | 2.5922 | 8.02 | 0.006 | −5.49 | −15.62 | −6.44 |
| NGC 4258 | 0.001 | SY2 | 43.45 | −7.98201 | 7.62 | 2.9822 | 10.33 | 0.148 | −4.97 | −15.10 | −5.92 |
| Name | z | Type | logLbol |
|
|
|
logTBH | zSeed | Jq | JURCA | Jπ |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 3C 120 | 0.033 | SY1 | 45.34 | −7.78201 | 7.42 | 2.7822 | 8.04 | 0.034 | −7.69 | −17.82 | −8.64 |
| 3C 390.3 | 0.056 | SY1 | 44.88 | −8.91201 | 8.55 | 3.9122 | 10.76 | 0.103 | −10.15 | −20.28 | −11.10 |
| Akn 120 | 0.032 | SY1 | 44.91 | −8.63201 | 8.27 | 3.6322 | 10.17 | 0.055 | −9.15 | −19.28 | −10.10 |
| F9 | 0.047 | SY1 | 45.23 | −8.27201 | 7.91 | 3.2722 | 9.13 | 0.052 | −8.87 | −19.00 | −9.82 |
| IC 4329A | 0.016 | SY1 | 44.78 | −7.13201 | 6.77 | 2.1322 | 7.30 | 0.017 | −5.91 | −16.04 | −6.86 |
| Mrk 79 | 0.022 | SY1 | 44.57 | −8.22201 | 7.86 | 3.2222 | 9.69 | 0.041 | −8.10 | −18.23 | −9.05 |
| Mrk 110 | 0.035 | SY1 | 44.71 | −7.18201 | 6.82 | 2.1822 | 7.47 | 0.036 | −6.69 | −16.82 | −7.64 |
| Mrk 335 | 0.026 | SY1 | 44.69 | −7.05201 | 6.69 | 2.0522 | 7.23 | 0.027 | −6.20 | −16.33 | −7.15 |
| Mrk 509 | 0.034 | SY1 | 45.03 | −8.22201 | 7.86 | 3.2222 | 9.23 | 0.041 | −8.49 | −18.62 | −9.44 |
| Mrk 590 | 0.026 | SY1 | 44.63 | −7.56201 | 7.20 | 2.5622 | 8.31 | 0.030 | −7.09 | −17.22 | −8.04 |
| Mrk 817 | 0.032 | SY1 | 44.99 | −7.96201 | 7.60 | 2.9622 | 8.75 | 0.036 | −7.98 | −18.11 | −8.93 |
| NGC 3227 | 0.004 | SY1 | 43.86 | −8.00201 | 7.64 | 3.0022 | 9.96 | 0.064 | −6.21 | −16.34 | −7.16 |
| NGC 3516 | 0.009 | SY1 | 44.29 | −7.72201 | 7.36 | 2.7222 | 8.97 | 0.021 | −6.43 | −16.56 | −7.38 |
| NGC 3783 | 0.010 | SY1 | 44.41 | −7.30201 | 6.94 | 2.3022 | 8.01 | 0.013 | −5.79 | −15.92 | −6.74 |
| NGC 4051 | 0.002 | SY1 | 43.56 | −6.49201 | 6.13 | 1.4922 | 7.24 | 0.006 | −2.96 | −13.10 | −3.91 |
| NGC 4151 | 0.003 | SY1 | 43.73 | −7.49201 | 7.13 | 2.4922 | 9.07 | 0.028 | −5.07 | −15.20 | −6.02 |
| NGC 4593 | 0.009 | SY1 | 44.09 | −7.27201 | 6.91 | 2.2722 | 8.27 | 0.016 | −5.64 | −15.77 | −6.59 |
| NGC 5548 | 0.017 | SY1 | 44.83 | −8.39201 | 8.03 | 3.3922 | 9.77 | 0.033 | −8.16 | −18.30 | −9.11 |
| NGC 7469 | 0.016 | SY1 | 45.28 | −7.20201 | 6.84 | 2.2022 | 6.94 | 0.016 | −6.03 | −16.16 | −6.98 |
| PG 0026 + 129 | 0.142 | RQQ | 45.39 | −7.94201 | 7.58 | 2.9422 | 8.31 | 0.144 | −9.35 | −19.48 | −10.30 |
| PG 0052 + 251 | 0.155 | RQQ | 45.93 | −8.77201 | 8.41 | 3.7722 | 9.43 | 0.158 | −10.89 | −21.02 | −11.84 |
| PG 0804 + 761 | 0.100 | RQQ | 45.93 | −8.60201 | 8.24 | 3.6022 | 9.09 | 0.102 | −10.16 | −20.29 | −11.11 |
| PG 0844 + 349 | 0.064 | RQQ | 45.36 | −7.74201 | 7.38 | 2.7422 | 7.94 | 0.065 | −8.23 | −18.36 | −9.18 |
| PG 0953 + 414 | 0.239 | RQQ | 46.16 | −8.60201 | 8.24 | 3.6022 | 8.86 | 0.240 | −11.04 | −21.17 | −11.99 |
| PG 1211 + 143 | 0.085 | RQQ | 45.81 | −7.85201 | 7.49 | 2.8522 | 7.71 | 0.085 | −8.69 | −18.82 | −9.64 |
| PG 1229 + 204 | 0.064 | RQQ | 45.01 | −8.92201 | 8.56 | 3.9222 | 10.65 | 0.099 | −10.29 | −20.42 | −11.24 |
| PG 1307 + 085 | 0.155 | RQQ | 45.83 | −8.26201 | 7.90 | 3.2622 | 8.51 | 0.156 | −9.99 | −20.12 | −10.94 |
| PG 1351 + 640 | 0.087 | RQQ | 45.50 | −8.84201 | 8.48 | 3.8422 | 10.00 | 0.097 | −10.44 | −20.57 | −11.39 |
| PG 1411 + 442 | 0.089 | RQQ | 45.58 | −7.93201 | 7.57 | 2.9322 | 8.10 | 0.090 | −8.87 | −19.00 | −9.82 |
| PG 1426 + 015 | 0.086 | RQQ | 45.19 | −8.28201 | 7.92 | 3.2822 | 9.19 | 0.091 | −9.45 | −19.58 | −10.40 |
| PG 1613 + 658 | 0.129 | RQQ | 45.66 | −8.98201 | 8.62 | 3.9822 | 10.12 | 0.138 | −11.07 | −21.20 | −12.02 |
| PG 1617 + 175 | 0.114 | RQQ | 45.52 | −8.24201 | 7.88 | 3.2422 | 8.78 | 0.116 | −9.65 | −19.78 | −10.60 |
| PG 1700 + 518 | 0.292 | RQQ | 46.56 | −8.67201 | 8.31 | 3.6722 | 8.60 | 0.293 | −11.38 | −21.51 | −12.33 |
| PG 2130 + 099 | 0.061 | RQQ | 45.47 | −8.10201 | 7.74 | 3.1022 | 8.55 | 0.063 | −8.81 | −18.94 | −9.76 |
| PG 1226 + 023 | 0.158 | RLQ | 47.35 | −7.58201 | 7.22 | 2.5822 | 5.63 | 0.158 | −8.82 | −18.95 | −9.77 |
| PG 1704 + 608 | 0.371 | RLQ | 46.33 | −8.59201 | 8.23 | 3.5922 | 8.67 | 0.372 | −11.50 | −21.64 | −12.45 |
| Name | z | Type | logLbol |
|
|
|
logTBH | zSeed | Jq | JURCA | Jπ |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Mrk 841 | 0.036 | SY1 | 45.84 | −8.46201 | 8.10 | 3.4622 | 8.90 | 0.038 | −8.96 | −19.09 | −9.91 |
| NGC 4253 | 0.013 | SY1 | 44.40 | −6.90201 | 6.54 | 1.9022 | 7.22 | 0.014 | −5.32 | −15.45 | −6.27 |
| NGC 6814 | 0.005 | SY1 | 43.92 | −7.64201 | 7.28 | 2.6422 | 9.18 | 0.028 | −5.78 | −15.91 | −6.73 |
| 0054 + 144 | 0.171 | RQQ | 45.47 | −9.26201 | 8.90 | 4.2622 | 10.87 | 0.198 | −11.84 | −21.97 | −12.79 |
| 0157 + 001 | 0.164 | RQQ | 45.62 | −8.06201 | 7.70 | 3.0622 | 8.32 | 0.165 | −9.70 | −19.83 | −10.65 |
| 0204 + 292 | 0.109 | RQQ | 45.05 | −7.03201 | 6.67 | 2.0322 | 6.83 | 0.109 | −7.49 | −17.62 | −8.44 |
| 0205 + 024 | 0.155 | RQQ | 45.45 | −8.22201 | 7.86 | 3.2222 | 8.81 | 0.158 | −9.92 | −20.05 | −10.87 |
| 0244 + 194 | 0.176 | RQQ | 45.51 | −8.39201 | 8.03 | 3.3922 | 9.09 | 0.179 | −10.35 | −20.48 | −11.30 |
| 0923 + 201 | 0.190 | RQQ | 46.22 | −9.30201 | 8.94 | 4.3022 | 10.20 | 0.195 | −12.02 | −22.15 | −12.97 |
| 1012 + 008 | 0.185 | RQQ | 45.51 | −8.15201 | 7.79 | 3.1522 | 8.61 | 0.187 | −9.98 | −20.11 | −10.93 |
| 1029 − 140 | 0.086 | RQQ | 46.03 | −9.44201 | 9.08 | 4.4422 | 10.67 | 0.097 | −11.48 | −21.61 | −12.43 |
| 1116 + 215 | 0.177 | RQQ | 46.02 | −8.57201 | 8.21 | 3.5722 | 8.94 | 0.179 | −10.67 | −20.80 | −11.62 |
| 1202 + 281 | 0.165 | RQQ | 45.39 | −8.65201 | 8.29 | 3.6522 | 9.73 | 0.173 | −10.74 | −20.87 | −11.69 |
| 1309 + 355 | 0.184 | RQQ | 45.39 | −8.36201 | 8.00 | 3.3622 | 8.91 | 0.186 | −10.34 | −20.47 | −11.29 |
| 1402 + 261 | 0.164 | RQQ | 45.13 | −7.65201 | 7.29 | 2.6522 | 7.99 | 0.165 | −8.98 | −19.11 | −9.93 |
| 1444 + 407 | 0.267 | RQQ | 45.93 | −8.42201 | 8.06 | 3.4222 | 8.73 | 0.268 | −10.84 | −20.97 | −11.79 |
| 1635 + 119 | 0.146 | RQQ | 45.13 | −8.46201 | 8.10 | 3.4622 | 9.61 | 0.155 | −10.28 | −20.41 | −11.23 |
| 0022 − 297 | 0.406 | RLQ | 44.98 | −8.27201 | 7.91 | 3.2722 | 9.38 | 0.414 | −11.05 | −21.18 | −12.00 |
| 0024 + 348 | 0.333 | RLQ | 45.31 | −6.73201 | 6.37 | 1.7322 | 5.97 | 0.333 | −8.13 | −18.26 | −9.08 |
| 0056 − 001 | 0.717 | RLQ | 46.54 | −9.07201 | 8.71 | 4.0722 | 9.42 | 0.718 | −13.13 | −23.26 | −14.08 |
| 0110 + 495 | 0.395 | RLQ | 45.78 | −8.70201 | 8.34 | 3.7022 | 9.44 | 0.399 | −11.77 | −21.90 | −12.72 |
| 0114 + 074 | 0.343 | RLQ | 44.02 | −7.16201 | 6.80 | 2.1622 | 8.12 | 0.349 | −8.91 | −19.04 | −9.86 |
| 0119 + 041 | 0.637 | RLQ | 45.57 | −8.74201 | 8.38 | 3.7422 | 9.73 | 0.643 | −12.41 | −22.54 | −13.36 |
| 0133 + 207 | 0.425 | RLQ | 45.83 | −9.88201 | 9.52 | 4.8822 | 11.75 | 0.474 | −13.92 | −24.05 | −14.87 |
| 0133 + 476 | 0.859 | RLQ | 46.69 | −9.09201 | 8.73 | 4.0922 | 9.31 | 0.860 | −13.40 | −23.53 | −14.35 |
| 0134 + 329 | 0.367 | RLQ | 46.44 | −9.10201 | 8.74 | 4.1022 | 9.58 | 0.369 | −12.38 | −22.52 | −13.33 |
| 0135 − 247 | 0.831 | RLQ | 46.64 | −9.49201 | 9.13 | 4.4922 | 10.16 | 0.834 | −14.06 | −24.19 | −15.01 |
| 0137 + 012 | 0.258 | RLQ | 45.22 | −8.93201 | 8.57 | 3.9322 | 10.46 | 0.280 | −11.70 | −21.83 | −12.65 |
| 0153 − 410 | 0.226 | RLQ | 44.74 | −7.92201 | 7.56 | 2.9222 | 8.92 | 0.233 | −9.79 | −19.92 | −10.74 |
| 0159 − 117 | 0.669 | RLQ | 46.84 | −9.63201 | 9.27 | 4.6322 | 10.24 | 0.672 | −14.03 | −24.16 | −14.98 |
| 0210 + 860 | 0.186 | RLQ | 44.92 | −6.90201 | 6.54 | 1.9022 | 6.70 | 0.186 | −7.80 | −17.93 | −8.75 |
| 0221 + 067 | 0.510 | RLQ | 44.94 | −7.65201 | 7.29 | 2.6522 | 8.18 | 0.512 | −10.23 | −20.36 | −11.18 |
| 0237 − 233 | 2.224 | RLQ | 47.72 | −8.88201 | 8.52 | 3.8822 | 7.86 | 2.224 | −14.39 | −24.52 | −15.34 |
| 0327 − 241 | 0.888 | RLQ | 46.01 | −8.96201 | 8.60 | 3.9622 | 9.73 | 0.892 | −13.22 | −23.35 | −14.17 |
| 0336 − 019 | 0.852 | RLQ | 46.32 | −9.34201 | 8.98 | 4.3422 | 10.18 | 0.857 | −13.83 | −23.96 | −14.78 |
| 0403 − 132 | 0.571 | RLQ | 46.47 | −9.43201 | 9.07 | 4.4322 | 10.21 | 0.575 | −13.48 | −23.61 | −14.43 |
| 0405 − 123 | 0.574 | RLQ | 47.40 | −9.83201 | 9.47 | 4.8322 | 10.08 | 0.575 | −14.19 | −24.32 | −15.14 |
| 0420 − 014 | 0.915 | RLQ | 47.00 | −9.39201 | 9.03 | 4.3922 | 9.60 | 0.916 | −14.01 | −24.14 | −14.96 |
| 0437 + 785 | 0.454 | RLQ | 46.15 | −9.15201 | 8.79 | 4.1522 | 9.97 | 0.458 | −12.72 | −22.85 | −13.67 |
| 0444 + 634 | 0.781 | RLQ | 46.12 | −8.89201 | 8.53 | 3.8922 | 9.48 | 0.784 | −12.93 | −23.06 | −13.88 |
| 0454 − 810 | 0.444 | RLQ | 45.32 | −8.49201 | 8.13 | 3.4922 | 9.48 | 0.450 | −11.54 | −21.67 | −12.49 |
| 0454 + 066 | 0.405 | RLQ | 45.12 | −7.78201 | 7.42 | 2.7822 | 8.26 | 0.407 | −10.19 | −20.32 | −11.14 |
| 0502 + 049 | 0.954 | RLQ | 46.36 | −9.24201 | 8.88 | 4.2422 | 9.94 | 0.957 | −13.80 | −23.93 | −14.75 |
| 0514 − 459 | 0.194 | RLQ | 45.36 | −7.91201 | 7.55 | 2.9122 | 8.28 | 0.196 | −9.61 | −19.74 | −10.56 |
| 0518 + 165 | 0.759 | RLQ | 46.34 | −8.89201 | 8.53 | 3.8922 | 9.26 | 0.761 | −12.89 | −23.02 | −13.84 |
| 0538 + 498 | 0.545 | RLQ | 46.43 | −9.94201 | 9.58 | 4.9422 | 11.27 | 0.559 | −14.32 | −24.45 | −15.27 |
| 0602 − 319 | 0.452 | RLQ | 45.69 | −9.38201 | 9.02 | 4.3822 | 10.89 | 0.473 | −13.11 | −23.25 | −14.07 |
| 0607 − 157 | 0.324 | RLQ | 46.30 | −9.04201 | 8.68 | 4.0422 | 9.60 | 0.326 | −12.14 | −22.27 | −13.09 |
| 0637 − 752 | 0.654 | RLQ | 47.16 | −9.77201 | 9.41 | 4.7722 | 10.20 | 0.656 | −14.24 | −24.37 | −15.19 |
| 0646 + 600 | 0.455 | RLQ | 45.58 | −9.10201 | 8.74 | 4.1022 | 10.44 | 0.469 | −12.63 | −22.76 | −13.58 |
| 0723 + 679 | 0.846 | RLQ | 46.41 | −9.03201 | 8.67 | 4.0322 | 9.47 | 0.848 | −13.27 | −23.41 | −14.23 |
| 0736 + 017 | 0.191 | RLQ | 46.41 | −8.36201 | 8.00 | 3.3622 | 8.57 | 0.192 | −10.38 | −20.51 | −11.33 |
| 0738 + 313 | 0.631 | RLQ | 46.94 | −9.76201 | 9.40 | 4.7622 | 10.40 | 0.634 | −14.18 | −24.31 | −15.13 |
| 0809 + 483 | 0.871 | RLQ | 46.54 | −8.32201 | 7.96 | 3.3222 | 7.92 | 0.871 | −12.07 | −22.20 | −13.02 |
| 0838 + 133 | 0.684 | RLQ | 46.23 | −8.88201 | 8.52 | 3.8822 | 9.35 | 0.686 | −12.74 | −22.87 | −13.69 |
| 0906 + 430 | 0.668 | RLQ | 45.99 | −8.26201 | 7.90 | 3.2622 | 8.35 | 0.669 | −11.63 | −21.76 | −12.58 |
| 0912 + 029 | 0.427 | RLQ | 45.26 | −8.08201 | 7.72 | 3.0822 | 8.72 | 0.430 | −10.77 | −20.90 | −11.72 |
| 0921 − 213 | 0.052 | RLQ | 44.63 | −8.50201 | 8.14 | 3.5022 | 10.19 | 0.084 | −9.36 | −19.50 | −10.32 |
| 0923 + 392 | 0.698 | RLQ | 46.26 | −9.64201 | 9.28 | 4.6422 | 10.84 | 0.708 | −14.10 | −24.23 | −15.05 |
| 0925 − 203 | 0.348 | RLQ | 46.35 | −8.82201 | 8.46 | 3.8222 | 9.11 | 0.349 | −11.83 | −21.97 | −12.78 |
| 0953 + 254 | 0.712 | RLQ | 46.59 | −9.36201 | 9.00 | 4.3622 | 9.95 | 0.715 | −13.63 | −23.76 | −14.58 |
| 0954 + 556 | 0.901 | RLQ | 46.54 | −8.43201 | 8.07 | 3.4322 | 8.14 | 0.901 | −12.31 | −22.44 | −13.26 |
| 1004 + 130 | 0.240 | RLQ | 46.21 | −9.46201 | 9.10 | 4.4622 | 10.53 | 0.248 | −12.55 | −22.68 | −13.50 |
| 1007 + 417 | 0.612 | RLQ | 46.71 | −9.15201 | 8.79 | 4.1522 | 9.41 | 0.613 | −13.08 | −23.21 | −14.03 |
| 1016 − 311 | 0.794 | RLQ | 46.63 | −9.25201 | 8.89 | 4.2522 | 9.69 | 0.796 | −13.58 | −23.71 | −14.53 |
| 1020 − 103 | 0.197 | RLQ | 44.87 | −8.72201 | 8.36 | 3.7222 | 10.39 | 0.228 | −11.04 | −21.18 | −11.99 |
| 1034 − 293 | 0.312 | RLQ | 46.20 | −9.11201 | 8.75 | 4.1122 | 9.84 | 0.316 | −12.22 | −22.35 | −13.17 |
| 1036 − 154 | 0.525 | RLQ | 44.55 | −8.16201 | 7.80 | 3.1622 | 9.59 | 0.543 | −11.16 | −21.29 | −12.11 |
| 1045 − 188 | 0.595 | RLQ | 45.80 | −7.19201 | 6.83 | 2.1922 | 6.40 | 0.595 | −9.61 | −19.74 | −10.56 |
| 1100 + 772 | 0.311 | RLQ | 46.49 | −9.67201 | 9.31 | 4.6722 | 10.67 | 0.318 | −13.20 | −23.33 | −14.15 |
| 1101 − 325 | 0.355 | RLQ | 46.33 | −8.97201 | 8.61 | 3.9722 | 9.43 | 0.357 | −12.12 | −22.25 | −13.07 |
| 1106 + 023 | 0.157 | RLQ | 44.97 | −7.86201 | 7.50 | 2.8622 | 8.57 | 0.160 | −9.31 | −19.44 | −10.26 |
| 1107 − 187 | 0.497 | RLQ | 44.25 | −7.26201 | 6.90 | 2.2622 | 8.09 | 0.501 | −9.52 | −19.65 | −10.47 |
| 1111 + 408 | 0.734 | RLQ | 46.26 | −10.18201 | 9.82 | 5.1822 | 11.92 | 0.770 | −15.11 | −25.24 | −16.06 |
| 1128 − 047 | 0.266 | RLQ | 44.08 | −7.08201 | 6.72 | 2.0822 | 7.90 | 0.270 | −8.49 | −18.62 | −9.44 |
| 1136 − 135 | 0.554 | RLQ | 46.78 | −9.14201 | 8.78 | 4.1422 | 9.32 | 0.555 | −12.94 | −23.07 | −13.89 |
| 1137 + 660 | 0.656 | RLQ | 46.85 | −9.72201 | 9.36 | 4.7222 | 10.41 | 0.659 | −14.16 | −24.29 | −15.11 |
| 1150 + 497 | 0.334 | RLQ | 45.98 | −9.09201 | 8.73 | 4.0922 | 10.02 | 0.340 | −12.26 | −22.39 | −13.21 |
| 1151 − 348 | 0.258 | RLQ | 45.56 | −9.38201 | 9.02 | 4.3822 | 11.02 | 0.287 | −12.26 | −22.39 | −13.21 |
| 1200 − 051 | 0.381 | RLQ | 46.41 | −8.77201 | 8.41 | 3.7722 | 8.95 | 0.382 | −12.26 | −22.39 | −13.21 |
| 1202 − 262 | 0.789 | RLQ | 45.81 | −9.36201 | 9.00 | 4.3622 | 10.73 | 0.804 | −13.76 | −23.89 | −14.71 |
| 1217 + 023 | 0.240 | RLQ | 45.83 | −8.77201 | 8.41 | 3.7722 | 9.53 | 0.244 | −11.34 | −21.47 | −12.29 |
| 1237 − 101 | 0.751 | RLQ | 46.63 | −9.64201 | 9.28 | 4.6422 | 10.47 | 0.755 | −14.19 | −24.32 | −15.14 |
| 1244 − 255 | 0.633 | RLQ | 46.48 | −9.40201 | 9.04 | 4.4022 | 10.14 | 0.637 | −13.55 | −23.69 | −14.51 |
| 1250 + 568 | 0.321 | RLQ | 45.61 | −8.78201 | 8.42 | 3.7822 | 9.77 | 0.327 | −11.67 | −21.81 | −12.62 |
| 1253 − 055 | 0.536 | RLQ | 46.10 | −8.79201 | 8.43 | 3.7922 | 9.30 | 0.538 | −12.28 | −22.42 | −13.24 |
| 1254 − 333 | 0.190 | RLQ | 45.52 | −9.19201 | 8.83 | 4.1922 | 10.68 | 0.210 | −11.83 | −21.96 | −12.78 |
| 1302 − 102 | 0.286 | RLQ | 45.86 | −8.66201 | 8.30 | 3.6622 | 9.28 | 0.289 | −11.34 | −21.47 | −12.29 |
| 1352 − 104 | 0.332 | RLQ | 45.81 | −8.51201 | 8.15 | 3.5122 | 9.03 | 0.334 | −11.24 | −21.37 | −12.19 |
| 1354 + 195 | 0.720 | RLQ | 47.11 | −9.80201 | 9.44 | 4.8022 | 10.31 | 0.722 | −14.42 | −24.55 | −15.37 |
| 1355 − 416 | 0.313 | RLQ | 46.48 | −10.09201 | 9.73 | 5.0922 | 11.52 | 0.331 | −13.94 | −24.07 | −14.89 |
| 1359 − 281 | 0.803 | RLQ | 46.19 | −8.43201 | 8.07 | 3.4322 | 8.49 | 0.804 | −12.16 | −22.29 | −13.11 |
| 1450 − 338 | 0.368 | RLQ | 43.94 | −6.82201 | 6.46 | 1.8222 | 7.52 | 0.371 | −8.40 | −18.53 | −9.35 |
| 1451 − 375 | 0.314 | RLQ | 46.16 | −9.18201 | 8.82 | 4.1822 | 10.02 | 0.319 | −12.35 | −22.48 | −13.30 |
| 1458 + 718 | 0.905 | RLQ | 46.93 | −9.34201 | 8.98 | 4.3422 | 9.57 | 0.906 | −13.91 | −24.04 | −14.86 |
| 1509 + 022 | 0.219 | RLQ | 44.54 | −8.35201 | 7.99 | 3.3522 | 9.98 | 0.247 | −10.51 | −20.64 | −11.46 |
| 1510 − 089 | 0.361 | RLQ | 46.38 | −9.01201 | 8.65 | 4.0122 | 9.46 | 0.363 | −12.21 | −22.34 | −13.16 |
| 1545 + 210 | 0.266 | RLQ | 45.86 | −9.29201 | 8.93 | 4.2922 | 10.54 | 0.278 | −12.36 | −22.49 | −13.31 |
| 1546 + 027 | 0.412 | RLQ | 46.00 | −9.08201 | 8.72 | 4.0822 | 9.98 | 0.417 | −12.48 | −22.61 | −13.43 |
| 1555 − 140 | 0.097 | RLQ | 44.94 | −7.61201 | 7.25 | 2.6122 | 8.10 | 0.099 | −8.39 | −18.53 | −9.34 |
| 1611 + 343 | 1.401 | RLQ | 46.99 | −9.93201 | 9.57 | 4.9322 | 10.69 | 1.405 | −15.54 | −25.67 | −16.49 |
| 1634 + 628 | 0.988 | RLQ | 45.47 | −7.64201 | 7.28 | 2.6422 | 7.63 | 0.989 | −11.05 | −21.18 | −12.00 |
| 1637 + 574 | 0.750 | RLQ | 46.68 | −9.54201 | 9.18 | 4.5422 | 10.22 | 0.753 | −14.01 | −24.14 | −14.96 |
| 1641 + 399 | 0.594 | RLQ | 46.89 | −9.78201 | 9.42 | 4.7822 | 10.49 | 0.597 | −14.14 | −24.27 | −15.09 |
| 1642 + 690 | 0.751 | RLQ | 45.78 | −8.12201 | 7.76 | 3.1222 | 8.28 | 0.752 | −11.53 | −21.66 | −12.48 |
| 1656 + 053 | 0.879 | RLQ | 47.21 | −9.98201 | 9.62 | 4.9822 | 10.57 | 0.882 | −14.99 | −25.12 | −15.94 |
| 1706 + 006 | 0.449 | RLQ | 44.01 | −6.99210 | 6.63 | 2.9922 | 7.79 | 0.453 | −8.92 | −19.06 | −9.87 |
| 1721 + 343 | 0.206 | RLQ | 45.63 | −8.40201 | 8.04 | 3.4022 | 8.99 | 0.209 | −10.53 | −20.66 | −11.48 |
| 1725 + 044 | 0.293 | RLQ | 46.07 | −8.43201 | 8.07 | 3.4322 | 8.61 | 0.294 | −10.96 | −21.09 | −11.91 |
| Name | z | Type | logLbol |
|
|
|
logTBH | zSeed | Jq | JURCA | Jπ |
|---|---|---|---|---|---|---|---|---|---|---|---|
| NGC 1566 | 0.005 | SY1 | 44.45 | −7.28201 | 6.92 | 2.2822 | 7.93 | 0.008 | −5.15 | −15.28 | −6.10 |
| NGC 2841 | 0.002 | SY1 | 43.67 | −8.57201 | 8.21 | 3.5722 | 11.29 | 0.347 | −6.60 | −16.74 | −7.55 |
| NGC 3982 | 0.004 | SY1 | 43.54 | −6.45201 | 6.09 | 1.45220 | 7.18 | 0.008 | −3.50 | −13.63 | −4.45 |
| NGC 3998 | 0.003 | SY1 | 43.54 | −9.31201 | 8.95 | 4.3122 | 12.90 | 2.561 | −8.25 | −18.38 | −9.20 |
| Mrk 10 | 0.029 | SY1 | 44.61 | −7.83291 | 7.47 | 4.7908 | 8.87 | 0.036 | −7.66 | −17.79 | −8.61 |
| UGC 3223 | 0.016 | SY1 | 44.27 | −7.38201 | 7.02 | 2.3822 | 8.31 | 0.022 | −6.34 | −16.47 | −7.29 |
| NGC 513 | 0.002 | SY2 | 42.52 | −8.01201 | 7.65 | 3.0122 | 11.32 | 1.345 | −5.62 | −15.76 | −6.57 |
| NGC 788 | 0.014 | SY2 | 44.33 | −7.87201 | 7.51 | 2.8722 | 9.23 | 0.029 | −7.08 | −17.21 | −8.03 |
| NGC 1052 | 0.005 | SY2 | 43.84 | −8.55201 | 8.19 | 3.5522 | 11.08 | 0.228 | −7.37 | −17.50 | −8.32 |
| NGC 1275 | 0.018 | SY2 | 45.04 | −8.87201 | 8.51 | 3.8722 | 10.52 | 0.047 | −9.05 | −19.19 | −10.01 |
| NGC 1320 | 0.009 | SY2 | 44.02 | −7.54201 | 7.18 | 2.5422 | 8.88 | 0.023 | −6.12 | −16.25 | −7.07 |
| NGC 1358 | 0.013 | SY2 | 44.37 | −8.24201 | 7.88 | 3.2422 | 9.93 | 0.045 | −7.66 | −17.80 | −8.62 |
| NGC 1386 | 0.003 | SY2 | 43.38 | −7.60201 | 7.24 | 2.6022 | 9.64 | 0.075 | −0.020 | −15.39 | −6.21 |
| NGC 1667 | 0.015 | SY2 | 44.69 | −8.24201 | 7.88 | 3.2422 | 9.61 | 0.030 | −7.79 | −17.92 | −8.74 |
| NGC 2110 | 0.008 | SY2 | 44.10 | −8.66201 | 8.30 | 3.6622 | 11.04 | 0.166 | −7.97 | −18.10 | −8.92 |
| NGC 2273 | 0.006 | SY2 | 44.05 | −7.66201 | 7.30 | 2.6622 | 9.09 | 0.024 | −5.97 | −16.10 | −6.92 |
| NGC 2992 | 0.008 | SY2 | 43.92 | −8.08201 | 7.72 | 3.0822 | 10.06 | 0.071 | −6.96 | −17.09 | −7.91 |
| NGC 3185 | 0.004 | SY2 | 43.08 | −6.42201 | 6.06 | 1.4222 | 7.58 | 0.014 | −3.45 | −13.58 | −4.40 |
| NGC 3362 | 0.028 | SY2 | 44.27 | −7.13201 | 6.77 | 2.1322 | 7.81 | 0.031 | −6.40 | −16.54 | −7.36 |
| NGC 3786 | 0.009 | SY2 | 43.47 | −7.89201 | 7.53 | 2.8922 | 10.13 | 0.123 | −6.73 | −16.86 | −7.68 |
| NGC 4117 | 0.003 | SY2 | 43.64 | −7.19201 | 6.83 | 2.1922 | 8.56 | 0.018 | −4.54 | −14.67 | −5.49 |
| NGC 4339 | 0.004 | SY2 | 43.38 | −7.76201 | 7.40 | 2.7622 | 9.96 | 0.108 | −5.79 | −15.92 | −6.74 |
| NGC 5194 | 0.002 | SY2 | 43.79 | −7.31201 | 6.95 | 2.3122 | 8.65 | 0.016 | −4.40 | −14.53 | −5.35 |
| NGC 5252 | 0.023 | SY2 | 45.39 | −8.40201 | 8.04 | 3.4022 | 9.23 | 0.027 | −8.45 | −18.58 | −9.40 |
| NGC 5273 | 0.004 | SY2 | 43.03 | −6.87201 | 6.51 | 1.8722 | 8.53 | 0.034 | −4.23 | −14.36 | −5.18 |
| NGC 5347 | 0.008 | SY2 | 43.81 | −7.15201 | 6.79 | 2.1522 | 8.31 | 0.018 | −5.33 | −15.46 | −6.28 |
| NGC 5427 | 0.009 | SY2 | 44.12 | −6.75201 | 6.39 | 1.7522 | 7.20 | 0.011 | −4.73 | −14.86 | −5.68 |
| NGC 5929 | 0.008 | SY2 | 43.04 | −7.61201 | 7.25 | 2.6122 | 10.00 | 0.169 | −6.13 | −16.27 | −7.09 |
| NGC 5953 | 0.007 | SY2 | 44.05 | −7.30201 | 6.94 | 2.3022 | 8.37 | 0.015 | −5.48 | −15.61 | −6.43 |
| NGC 6104 | 0.028 | SY2 | 43.60 | −7.96201 | 7.60 | 2.9622 | 10.14 | 0.128 | −7.86 | −17.99 | −8.81 |
| NGC 7213 | 0.006 | SY2 | 44.30 | −8.35201 | 7.99 | 3.3522 | 10.22 | 0.055 | −7.18 | −17.31 | −8.13 |
| NGC 7319 | 0.023 | SY2 | 44.19 | −7.74201 | 7.38 | 2.7422 | 9.11 | 0.038 | −7.30 | −17.43 | −8.25 |
| NGC 7603 | 0.030 | SY2 | 44.66 | −8.44201 | 8.08 | 3.4422 | 10.04 | 0.056 | −8.76 | −18.89 | −9.71 |
| NGC 7672 | 0.013 | SY2 | 43.86 | −7.24201 | 6.88 | 2.2422 | 8.44 | 0.023 | −5.91 | −16.05 | −6.87 |
| NGC 7682 | 0.017 | SY2 | 43.93 | −7.64201 | 7.28 | 2.6422 | 9.17 | 0.039 | −6.85 | −16.98 | −7.80 |
| NGC 7743 | 0.006 | SY2 | 43.60 | −6.95201 | 6.59 | 1.9522 | 8.12 | 0.016 | −4.73 | −14.86 | −5.68 |
| Mrk 1 | 0.016 | SY2 | 44.20 | −7.52201 | 7.16 | 2.5222 | 8.66 | 0.025 | −6.59 | −16.72 | −7.54 |
| Mrk 3 | 0.014 | SY2 | 44.54 | −9.01201 | 8.65 | 4.0122 | 11.30 | 0.142 | −9.08 | −19.21 | −10.03 |
| Mrk 78 | 0.037 | SY2 | 44.59 | −8.23201 | 7.87 | 3.2322 | 9.69 | 0.056 | −8.58 | −18.71 | −9.53 |
| Mrk 270 | 0.010 | SY2 | 43.37 | −7.96201 | 7.60 | 2.9622 | 10.37 | 0.179 | −6.94 | −17.07 | −7.89 |
| Mrk 348 | 0.015 | SY2 | 44.27 | −7.57201 | 7.21 | 2.5722 | 8.69 | 0.024 | −6.62 | −16.75 | −7.57 |
| Mrk 533 | 0.029 | SY2 | 45.15 | −7.92201 | 7.56 | 2.9222 | 8.51 | 0.032 | −7.82 | −17.95 | −8.77 |
| Mrk 573 | 0.017 | SY2 | 44.44 | −7.64201 | 7.28 | 2.6422 | 8.66 | 0.024 | −6.85 | −16.98 | −7.80 |
| Mrk 622 | 0.023 | SY2 | 44.52 | −7.28201 | 6.92 | 2.2822 | 7.86 | 0.026 | −6.49 | −16.62 | −7.44 |
| Mrk 686 | 0.014 | SY2 | 44.11 | −7.92201 | 7.56 | 2.9222 | 9.55 | 0.042 | −7.17 | −17.30 | −8.12 |
| Mrk 917 | 0.024 | SY2 | 44.75 | −7.98201 | 7.62 | 2.9822 | 9.03 | 0.031 | −7.75 | −17.89 | −8.70 |
| Mrk 1018 | 0.042 | SY2 | 44.39 | −8.45201 | 8.09 | 3.4522 | 10.33 | 0.092 | −9.08 | −19.21 | −10.03 |
| Mrk 1040 | 0.017 | SY2 | 44.53 | −8.00201 | 7.64 | 3.0022 | 9.29 | 0.030 | −7.48 | −17.61 | −8.43 |
| Mrk 1066 | 0.012 | SY2 | 44.55 | −7.37201 | 7.01 | 2.3722 | 8.01 | 0.015 | −6.07 | −16.20 | −7.02 |
| Mrk 1157 | 0.015 | SY2 | 44.27 | −7.19201 | 6.83 | 2.1922 | 7.93 | 0.019 | −5.95 | −16.08 | −6.90 |
| Akn 79 | 0.018 | SY2 | 45.24 | −7.90201 | 7.54 | 2.9022 | 8.38 | 0.020 | −7.36 | −17.49 | −8.31 |
| Akn 347 | 0.023 | SY2 | 44.84 | −8.36201 | 8.00 | 3.3622 | 9.70 | 0.037 | −8.38 | −18.51 | −9.33 |
| IC 5063 | 0.011 | SY2 | 44.53 | −8.10201 | 7.74 | 3.1022 | 9.49 | 0.027 | −7.27 | −17.40 | −8.22 |
| II ZW55 | 0.025 | SY2 | 44.54 | −8.59201 | 8.23 | 3.5922 | 10.46 | 0.074 | −8.86 | −18.99 | −9.81 |
| F 341 | 0.016 | SY2 | 44.13 | −7.51201 | 7.15 | 2.5122 | 8.71 | 0.026 | −6.57 | −16.70 | −7.52 |
| UGC 3995 | 0.016 | SY2 | 44.39 | −8.05201 | 7.69 | 3.0522 | 9.53 | 0.036 | −7.52 | −17.65 | −8.47 |
| UGC 6100 | 0.029 | SY2 | 44.48 | −8.06201 | 7.70 | 3.0622 | 9.46 | 0.046 | −8.06 | −18.20 | −9.01 |
| 1ES 1959 + 65 | 0.048 | BLL | — | −10.39501 | 8.09 | 3.4522 | 7.79 | 0.052 | −9.20 | −19.34 | −10.15 |
| Mrk 180 | 0.045 | BLL | — | −10.51501 | 8.21 | 3.5722 | 7.91 | 0.051 | −9.35 | −19.49 | −10.31 |
| Mrk 421 | 0.031 | BLL | — | −10.59501 | 8.29 | 3.6522 | 7.99 | 0.038 | −9.16 | −19.29 | −10.11 |
| Mrk 501 | 0.034 | BLL | — | −11.51501 | 9.21 | 4.5722 | 8.91 | 0.092 | −10.85 | −20.98 | −11.80 |
| I Zw 187 | 0.055 | BLL | — | −10.16501 | 7.86 | 3.2222 | 7.56 | 0.058 | −8.93 | −19.06 | −9.88 |
| 3C 371 | 0.051 | BLL | — | −10.81501 | 8.51 | 3.8722 | 8.21 | 0.063 | −9.99 | −20.13 | −10.95 |
| 1514 − 241 | 0.049 | BLL | — | −10.40501 | 8.10 | 3.4622 | 7.80 | 0.054 | −9.24 | −19.37 | −10.19 |
| 0521 − 365 | 0.055 | BLL | — | −10.95501 | 8.65 | 4.0122 | 8.35 | 0.071 | −10.31 | −20.44 | −11.26 |
| 0548 − 322 | 0.069 | BLL | — | −10.45501 | 8.15 | 3.5122 | 7.85 | 0.074 | −9.65 | −19.78 | −10.60 |
| 0706 + 591 | 0.125 | BLL | — | −10.56501 | 8.26 | 3.6222 | 7.96 | 0.132 | −10.41 | −20.54 | −11.36 |
| 2201 + 044 | 0.027 | BLL | — | −10.40501 | 8.10 | 3.4622 | 7.80 | 0.032 | −8.70 | −18.83 | −9.65 |
| 2344 + 514 | 0.044 | BLL | — | −11.10501 | 8.80 | 4.1622 | 8.50 | 0.067 | −10.37 | −20.50 | −11.32 |
| 3C 29 | 0.045 | RG | — | −10.50501 | 8.20 | 3.5622 | 7.90 | 0.051 | −9.34 | −19.47 | −10.29 |
| 3C 31 | 0.017 | RG | — | −10.80501 | 8.50 | 3.8622 | 8.20 | 0.028 | −8.99 | −19.12 | −9.94 |
| 3C 33 | 0.059 | RG | — | −10.68501 | 8.38 | 3.7422 | 8.08 | 0.068 | −9.90 | −20.03 | −10.85 |
| 3C 40 | 0.018 | RG | — | −10.16501 | 7.86 | 3.2222 | 7.56 | 0.021 | −7.92 | −18.05 | −8.87 |
| 3C 62 | 0.148 | RG | — | −10.97501 | 8.67 | 4.0322 | 8.37 | 0.165 | −11.29 | −21.43 | −12.25 |
| 3C 76.1 | 0.032 | RG | — | −10.43501 | 8.13 | 3.4922 | 7.83 | 0.037 | −8.90 | −19.04 | −9.86 |
| 3C 78 | 0.029 | RG | — | −10.90501 | 8.60 | 3.9622 | 8.30 | 0.043 | −9.64 | −19.77 | −10.59 |
| 3C 84 | 0.017 | RG | — | −10.79501 | 8.49 | 3.8522 | 8.19 | 0.028 | −8.97 | −19.10 | −9.92 |
| 3C 88 | 0.030 | RG | — | −10.33501 | 8.03 | 3.3922 | 7.73 | 0.034 | −8.67 | −18.80 | −9.62 |
| 3C 89 | 0.139 | RG | — | −10.82501 | 8.52 | 3.8822 | 8.22 | 0.151 | −10.97 | −21.10 | −11.92 |
| 3C 98 | 0.031 | RG | — | −10.18501 | 7.88 | 3.2422 | 7.58 | 0.034 | −8.44 | −18.57 | −9.39 |
| 3C 120 | 0.033 | RG | — | −10.43501 | 8.13 | 3.4922 | 7.83 | 0.038 | −8.93 | −19.06 | −9.88 |
| 3C 192 | 0.060 | RG | — | −10.36501 | 8.06 | 3.4222 | 7.76 | 0.064 | −9.36 | −19.49 | −10.31 |
| 3C 196.1 | 0.198 | RG | — | −10.51501 | 8.21 | 3.5722 | 7.91 | 0.204 | −10.79 | −20.92 | −11.74 |
| 3C 223 | 0.137 | RG | — | −10.45501 | 8.15 | 3.5122 | 7.85 | 0.142 | −10.31 | −20.44 | −11.26 |
| 3C 293 | 0.045 | RG | — | −10.29501 | 7.99 | 3.3522 | 7.69 | 0.048 | −8.97 | −19.10 | −9.92 |
| 3C 305 | 0.041 | RG | — | −10.22501 | 7.92 | 3.2822 | 7.62 | 0.044 | −8.76 | −18.89 | −9.71 |
| 3C 338 | 0.030 | RG | — | −11.08501 | 8.78 | 4.1422 | 8.48 | 0.052 | −9.98 | −20.12 | −10.93 |
| 3C 388 | 0.091 | RG | — | −11.48501 | 9.18 | 4.5422 | 8.88 | 0.145 | −11.71 | −21.84 | −12.66 |
| 3C 444 | 0.153 | RG | — | −9.98501 | 7.68 | 3.0422 | 7.38 | 0.155 | −9.60 | −19.73 | −10.55 |
| 3C 449 | 0.017 | RG | — | −10.63501 | 8.33 | 3.6922 | 8.03 | 0.025 | −8.69 | −18.82 | −9.64 |
| gin 116 | 0.033 | RG | — | −11.05501 | 8.75 | 4.1122 | 8.45 | 0.053 | −10.02 | −20.15 | −10.97 |
| NGC 315 | 0.017 | RG | — | −11.20501 | 8.90 | 4.2622 | 8.60 | 0.045 | −9.69 | −19.82 | −10.64 |
| NGC 507 | 0.017 | RG | — | −11.30501 | 9.00 | 4.3622 | 8.70 | 0.053 | −9.86 | −19.99 | −10.81 |
| NGC 708 | 0.016 | RG | — | −10.76501 | 8.46 | 3.8222 | 8.16 | 0.026 | −8.86 | −18.99 | −9.81 |
| NGC 741 | 0.018 | RG | — | −11.02501 | 8.72 | 4.0822 | 8.42 | 0.037 | −9.42 | −19.55 | −10.37 |
| NGC 4839 | 0.023 | RG | — | −10.78501 | 8.48 | 3.8422 | 8.18 | 0.034 | −9.22 | −19.35 | −10.17 |
| NGC 4869 | 0.023 | RG | — | −10.42501 | 8.12 | 3.4822 | 7.82 | 0.028 | −8.59 | −18.72 | −9.54 |
| NGC 4874 | 0.024 | RG | — | −10.93501 | 8.63 | 3.9922 | 8.33 | 0.039 | −9.52 | −19.65 | −10.47 |
| NGC 6086 | 0.032 | RG | — | −11.26501 | 8.96 | 4.3222 | 8.66 | 0.065 | −10.36 | −20.49 | −11.31 |
| NGC 6137 | 0.031 | RG | — | −11.11501 | 8.81 | 4.1722 | 8.51 | 0.054 | −10.07 | −20.20 | −11.02 |
| NGC 7626 | 0.025 | RG | — | −11.27501 | 8.97 | 4.3322 | 8.67 | 0.058 | −10.15 | −20.28 | −11.10 |
| 0039 − 095 | 0.000 | RG | — | −11.02501 | 8.72 | 4.0822 | 8.42 | 0.019 | −2.89 | −13.02 | −3.84 |
| 0053 − 015 | 0.038 | RG | — | −11.12501 | 8.82 | 4.1822 | 8.52 | 0.062 | −10.27 | −20.40 | −11.22 |
| 0053 − 016 | 0.043 | RG | — | −10.81501 | 8.51 | 3.8722 | 8.21 | 0.055 | −9.84 | −19.97 | −10.79 |
| 0055 − 016 | 0.045 | RG | — | −11.15501 | 8.85 | 4.2122 | 8.55 | 0.070 | −10.47 | −20.61 | −11.43 |
| 0110 + 152 | 0.044 | RG | — | −10.39501 | 8.09 | 3.4522 | 7.79 | 0.048 | −9.12 | −19.26 | −10.07 |
| 0112 − 000 | 0.045 | RG | — | −10.83501 | 8.53 | 3.8922 | 8.23 | 0.057 | −9.91 | −20.05 | −10.87 |
| 0112 + 084 | 0.000 | RG | — | −11.48501 | 9.18 | 4.5422 | 8.88 | 0.054 | −3.70 | −13.83 | −4.65 |
| 0147 + 360 | 0.018 | RG | — | −10.76501 | 8.46 | 3.8222 | 8.16 | 0.028 | −3.70 | −13.83 | −4.65 |
| 0131 − 360 | 0.030 | RG | — | −10.83501 | 8.53 | 3.8922 | 8.23 | 0.042 | −9.55 | −19.68 | −10.50 |
| 0257 − 398 | 0.066 | RG | — | −10.59501 | 8.29 | 3.6522 | 7.99 | 0.073 | −9.85 | −19.98 | −10.80 |
| 0306 + 237 | 0.000 | RG | — | −10.81501 | 8.51 | 3.8722 | 8.21 | 0.012 | −2.52 | −12.66 | −3.48 |
| 0312 − 343 | 0.067 | RG | — | −10.87501 | 8.57 | 3.9322 | 8.27 | 0.080 | −10.35 | −20.48 | −11.30 |
| 0325 + 024 | 0.030 | RG | — | −10.59501 | 8.29 | 3.6522 | 7.99 | 0.037 | −9.13 | −19.26 | −10.08 |
| 0431 − 133 | 0.033 | RG | — | −10.95501 | 8.65 | 4.0122 | 8.35 | 0.049 | −9.84 | −19.97 | −10.79 |
| 0431 − 134 | 0.035 | RG | — | −10.61501 | 8.31 | 3.6722 | 8.01 | 0.042 | −9.30 | −19.43 | −10.25 |
| 0449 − 175 | 0.031 | RG | — | −10.02501 | 7.72 | 3.0822 | 7.42 | 0.033 | −8.16 | −18.29 | −9.11 |
| 0546 − 329 | 0.037 | RG | — | −11.59501 | 9.29 | 4.6522 | 8.99 | 0.107 | −11.07 | −21.20 | −12.02 |
| 0548 − 317 | 0.034 | RG | — | −9.58501 | 7.28 | 2.6422 | 6.98 | 0.035 | −7.47 | −17.60 | −8.42 |
| 0634 − 206 | 0.056 | RG | — | −10.39501 | 8.09 | 3.4522 | 7.79 | 0.060 | −9.35 | −19.48 | −10.30 |
| 0718 − 340 | 0.029 | RG | — | −11.31501 | 9.01 | 4.3722 | 8.71 | 0.066 | −10.36 | −20.49 | −11.31 |
| 0915 − 118 | 0.054 | RG | — | −10.99501 | 8.69 | 4.0522 | 8.39 | 0.072 | −10.36 | −20.49 | −11.31 |
| 0940 − 304 | 0.038 | RG | — | −11.59501 | 9.29 | 4.6522 | 8.99 | 0.108 | −11.09 | −21.22 | −12.04 |
| 1043 − 290 | 0.060 | RG | — | −10.67501 | 8.37 | 3.7322 | 8.07 | 0.068 | −9.90 | −20.03 | −10.85 |
| 1107 − 372 | 0.010 | RG | — | −11.11501 | 8.81 | 4.1722 | 8.51 | 0.033 | −9.06 | −19.19 | −10.01 |
| 1123 − 351 | 0.032 | RG | — | −11.83501 | 9.53 | 4.8922 | 9.23 | 0.153 | −11.35 | −21.49 | −12.31 |
| 1258 − 321 | 0.015 | RG | — | −10.91501 | 8.61 | 3.9722 | 8.31 | 0.030 | −9.07 | −19.20 | −10.02 |
| 1333 − 337 | 0.013 | RG | — | −11.07501 | 8.77 | 4.1322 | 8.47 | 0.034 | −9.22 | −19.35 | −10.17 |
| 1400 − 337 | 0.014 | RG | — | −11.19501 | 8.89 | 4.2522 | 8.59 | 0.042 | −9.50 | −19.63 | −10.45 |
| 1404 − 267 | 0.022 | RG | — | −11.11505 | 8.81 | 4.8798 | 8.51 | 0.045 | −9.76 | −19.89 | −10.71 |
| 1510 + 076 | 0.053 | RG | — | −11.33501 | 9.03 | 4.3922 | 8.73 | 0.091 | −10.94 | −21.07 | −11.89 |
| 1514 + 072 | 0.035 | RG | — | −10.95501 | 8.65 | 4.0122 | 8.35 | 0.051 | −9.90 | −20.03 | −10.85 |
| 1520 + 087 | 0.034 | RG | — | −10.59501 | 8.29 | 3.6522 | 7.99 | 0.041 | −9.24 | −19.37 | −10.19 |
| 1521 − 300 | 0.020 | RG | — | −10.10501 | 7.80 | 3.1622 | 7.50 | 0.022 | −7.91 | −18.04 | −8.86 |
| 1602 + 178 | 0.041 | RG | — | −10.54501 | 8.24 | 3.6022 | 7.94 | 0.047 | −9.32 | −19.45 | −10.27 |
| 1610 + 296 | 0.032 | RG | — | −11.26501 | 8.96 | 4.3222 | 8.66 | 0.065 | −10.36 | −20.49 | −11.31 |
| 2236 − 176 | 0.070 | RG | — | −10.79501 | 8.49 | 3.8522 | 8.19 | 0.081 | −10.25 | −20.39 | −11.20 |
| 2322 + 143 | 0.045 | RG | — | −10.47501 | 8.17 | 3.5322 | 7.87 | 0.050 | −9.28 | −19.42 | −10.24 |
| 2322 − 122 | 0.082 | RG | — | −10.63501 | 8.33 | 3.6922 | 8.03 | 0.090 | −10.12 | −20.25 | −11.07 |
| 2333 − 327 | 0.052 | RG | — | −10.95501 | 8.65 | 4.0122 | 8.35 | 0.068 | −10.26 | −20.39 | −11.21 |
| 2335 + 267 | 0.030 | RG | — | −11.38501 | 9.08 | 4.4422 | 8.78 | 0.073 | −10.51 | −20.64 | −11.46 |
| Name | z | Type |
|
|
|
logTBH | zSeed | Jq | JURCA | Jπ |
|---|---|---|---|---|---|---|---|---|---|---|
| 0122 + 090 | 0.339 | BLL | −11.12501 | 8.82 | 4.1822 | 8.52 | 0.363 | −12.43 | −22.57 | −13.39 |
| 0145 + 138 | 0.124 | BLL | −10.72501 | 8.42 | 3.7822 | 8.12 | 0.133 | −10.68 | −20.81 | −11.63 |
| 0158 + 001 | 0.229 | BLL | −10.38501 | 8.08 | 3.4422 | 7.78 | 0.233 | −10.71 | −20.84 | −11.66 |
| 0229 + 200 | 0.139 | BLL | −11.54501 | 9.24 | 4.6022 | 8.94 | 0.201 | −12.23 | −22.36 | −13.18 |
| 0257 + 342 | 0.247 | BLL | −10.96501 | 8.66 | 4.0222 | 8.36 | 0.263 | −11.81 | −21.94 | −12.76 |
| 0317 + 183 | 0.190 | BLL | −10.25501 | 7.95 | 3.3122 | 7.65 | 0.193 | −10.29 | −20.42 | −11.24 |
| 0331 − 362 | 0.308 | BLL | −11.05501 | 8.75 | 4.1122 | 8.45 | 0.328 | −12.21 | −22.34 | −13.16 |
| 0347 − 121 | 0.188 | BLL | −10.95501 | 8.65 | 4.0122 | 8.35 | 0.204 | −11.50 | −21.63 | −12.45 |
| 0350 − 371 | 0.165 | BLL | −11.12501 | 8.82 | 4.1822 | 8.52 | 0.189 | −11.67 | −21.80 | −12.62 |
| 0414 + 009 | 0.287 | BLL | −10.86501 | 8.56 | 3.9222 | 8.26 | 0.300 | −11.80 | −21.93 | −12.75 |
| 0419 + 194 | 0.512 | BLL | −10.91501 | 8.61 | 3.9722 | 8.31 | 0.527 | −12.54 | −22.68 | −13.50 |
| 0506 − 039 | 0.304 | BLL | −11.05501 | 8.75 | 4.1122 | 8.45 | 0.324 | −12.19 | −22.32 | −13.14 |
| 0525 + 713 | 0.249 | BLL | −11.33501 | 9.03 | 4.3922 | 8.73 | 0.287 | −12.46 | −22.60 | −13.41 |
| 0607 + 710 | 0.267 | BLL | −10.95501 | 8.65 | 4.0122 | 8.35 | 0.283 | −12.46 | −22.60 | −13.41 |
| 0737 + 744 | 0.315 | BLL | −11.24501 | 8.94 | 4.3022 | 8.64 | 0.346 | −12.56 | −22.69 | −13.51 |
| 0922 + 749 | 0.638 | BLL | −11.91501 | 9.61 | 4.9722 | 9.31 | 0.784 | −14.56 | −24.69 | −15.51 |
| 0927 + 500 | 0.188 | BLL | −10.64501 | 8.34 | 3.7022 | 8.04 | 0.196 | −10.96 | −21.09 | −11.91 |
| 0958 + 210 | 0.344 | BLL | −11.33501 | 9.03 | 4.3922 | 8.73 | 0.382 | −12.82 | −22.95 | −13.77 |
| 1104 + 384 | 0.031 | BLL | −11.69501 | 9.39 | 4.7522 | 9.09 | 0.119 | −11.08 | −21.21 | −12.03 |
| 1133 + 161 | 0.460 | BLL | −10.62501 | 8.32 | 3.6822 | 8.02 | 0.467 | −11.91 | −22.04 | −12.86 |
| 1136 + 704 | 0.045 | BLL | −11.25501 | 8.95 | 4.3122 | 8.65 | 0.077 | −10.65 | −20.78 | −11.60 |
| 1207 + 394 | 0.615 | BLL | −11.40501 | 9.10 | 4.4622 | 8.80 | 0.660 | −13.62 | −23.76 | −14.58 |
| 1212 + 078 | 0.136 | BLL | −11.29501 | 8.99 | 4.3522 | 8.69 | 0.171 | −11.77 | −21.90 | −12.72 |
| 1215 + 303 | 0.130 | BLL | −10.42501 | 8.12 | 3.4822 | 7.82 | 0.135 | −10.20 | −20.33 | −11.15 |
| 1218 + 304 | 0.182 | BLL | −10.88501 | 8.58 | 3.9422 | 8.28 | 0.196 | −11.35 | −21.48 | −12.30 |
| 1221 + 245 | 0.218 | BLL | −10.27501 | 7.97 | 3.3322 | 7.67 | 0.221 | −10.47 | −20.60 | −11.42 |
| 1229 + 643 | 0.164 | BLL | −11.71501 | 9.41 | 4.7722 | 9.11 | 0.256 | −12.69 | −22.82 | −13.64 |
| 1248 − 296 | 0.370 | BLL | −11.31501 | 9.01 | 4.3722 | 8.71 | 0.407 | −12.87 | −23.00 | −13.82 |
| 1255 + 244 | 0.141 | BLL | −10.88501 | 8.58 | 3.9422 | 8.28 | 0.155 | −11.09 | −21.22 | −12.04 |
| 1407 + 595 | 0.495 | BLL | −11.60501 | 9.30 | 4.6622 | 9.00 | 0.566 | −13.71 | −23.84 | −14.66 |
| 1418 + 546 | 0.152 | BLL | −11.33501 | 9.03 | 4.3922 | 8.73 | 0.190 | −11.95 | −22.08 | −12.90 |
| 1426 + 428 | 0.129 | BLL | −11.43501 | 9.13 | 4.4922 | 8.83 | 0.177 | −11.96 | −22.09 | −12.91 |
| 1440 + 122 | 0.162 | BLL | −10.74501 | 8.44 | 3.8022 | 8.14 | 0.172 | −10.98 | −21.11 | −11.93 |
| 1534 + 014 | 0.312 | BLL | −11.10501 | 8.80 | 4.1622 | 8.50 | 0.335 | −12.31 | −22.44 | −13.26 |
| 1704 + 604 | 0.280 | BLL | −11.07501 | 8.77 | 4.1322 | 8.47 | 0.301 | −12.14 | −22.27 | −13.09 |
| 1728 + 502 | 0.055 | BLL | −10.43501 | 8.13 | 3.4922 | 7.83 | 0.060 | −9.40 | −19.53 | −10.35 |
| 1757 + 703 | 0.407 | BLL | −11.05501 | 8.75 | 4.1122 | 8.45 | 0.427 | −12.52 | −22.65 | −13.47 |
| 1807 + 698 | 0.051 | BLL | −12.40501 | 10.10 | 5.4622 | 9.80 | 0.502 | −12.78 | −22.91 | −13.73 |
| 1853 + 671 | 0.212 | BLL | −10.53501 | 8.23 | 3.5922 | 7.93 | 0.218 | −10.89 | −21.02 | −11.84 |
| 2005 − 489 | 0.071 | BLL | −11.33501 | 9.03 | 4.3922 | 8.73 | 0.109 | −11.21 | −21.34 | −12.16 |
| 2143 + 070 | 0.237 | BLL | −10.76501 | 8.46 | 3.8222 | 8.16 | 0.247 | −11.41 | −21.54 | −12.36 |
| 2200 + 420 | 0.069 | BLL | −10.53501 | 8.23 | 3.5922 | 7.93 | 0.075 | −9.79 | −19.92 | −10.74 |
| 2254 + 074 | 0.190 | BLL | −10.92501 | 8.62 | 3.9822 | 8.32 | 0.205 | −11.46 | −21.59 | −12.41 |
| 2326 + 174 | 0.213 | BLL | −11.04501 | 8.74 | 4.1022 | 8.44 | 0.233 | −11.79 | −21.92 | −12.74 |
| 2356 − 309 | 0.165 | BLL | −10.90501 | 8.60 | 3.9622 | 8.30 | 0.179 | −11.28 | −21.41 | −12.23 |
| 0230 − 027 | 0.239 | RG | −10.27501 | 7.97 | 3.3322 | 7.67 | 0.242 | −10.56 | −20.70 | −11.52 |
| 0307 + 169 | 0.256 | RG | −10.96501 | 8.66 | 4.0222 | 8.36 | 0.272 | −11.85 | −21.98 | −12.80 |
| 0345 + 337 | 0.244 | RG | −9.42501 | 7.12 | 2.4822 | 6.82 | 0.244 | −9.10 | −19.23 | −10.05 |
| 0917 + 459 | 0.174 | RG | −10.51501 | 8.21 | 3.5722 | 7.91 | 0.180 | −10.65 | −20.78 | −11.60 |
| 0958 + 291 | 0.185 | RG | −10.23501 | 7.93 | 3.2922 | 7.63 | 0.188 | −10.23 | −20.36 | −11.18 |
| 1215 − 033 | 0.184 | RG | −10.23501 | 7.93 | 3.2922 | 7.63 | 0.187 | −10.22 | −20.35 | −11.17 |
| 1215 + 013 | 0.118 | RG | −10.50501 | 8.20 | 3.5622 | 7.90 | 0.124 | −10.25 | −20.38 | −11.20 |
| 1330 + 022 | 0.215 | RG | −10.12501 | 7.82 | 3.1822 | 7.52 | 0.217 | −10.19 | −20.32 | −11.14 |
| 1342 − 016 | 0.167 | RG | −10.71501 | 8.41 | 3.7722 | 8.11 | 0.176 | −10.96 | −21.09 | −11.91 |
| 2141 + 279 | 0.215 | RG | −10.12501 | 7.82 | 3.1822 | 7.52 | 0.217 | −10.19 | −20.32 | −11.14 |
| 0257 + 024 | 0.115 | RQQ | −11.05501 | 8.75 | 4.1122 | 8.45 | 0.135 | −11.18 | −21.32 | −12.13 |
| 1549 + 203 | 0.250 | RQQ | −9.22501 | 6.92 | 2.2822 | 6.62 | 0.250 | −8.78 | −18.91 | −9.73 |
| 2215 − 037 | 0.241 | RQQ | −10.50501 | 8.20 | 3.5622 | 7.90 | 0.247 | −10.98 | −21.11 | −11.93 |
| 2344 + 184 | 0.138 | RQQ | −9.37501 | 7.07 | 2.4322 | 6.77 | 0.138 | −8.42 | −18.56 | −9.38 |
| 0958 + 291 | 0.185 | RG | −10.23501 | 7.93 | 3.2922 | 7.63 | 0.188 | −10.23 | −20.36 | −11.18 |
| 1215 − 033 | 0.184 | RG | −10.23501 | 7.93 | 3.2922 | 7.63 | 0.187 | −10.22 | −20.35 | −11.17 |
| 1215 + 013 | 0.118 | RG | −10.50501 | 8.20 | 3.5622 | 7.90 | 0.124 | −10.25 | −20.38 | −11.20 |
| 1330 + 022 | 0.215 | RG | −10.12501 | 7.82 | 3.1822 | 7.52 | 0.217 | −10.19 | −20.32 | −11.14 |
| 1342 − 016 | 0.167 | RG | −10.71501 | 8.41 | 3.7722 | 8.11 | 0.176 | −10.96 | −21.09 | −11.91 |
| 2141 + 279 | 0.215 | RG | −10.12501 | 7.82 | 3.1822 | 7.52 | 0.217 | −10.19 | −20.32 | −11.14 |
| 0257 + 024 | 0.115 | RQQ | −11.05501 | 8.75 | 4.1122 | 8.45 | 0.135 | −11.18 | −21.32 | −12.13 |
| 1549 + 203 | 0.250 | RQQ | −9.22501 | 6.92 | 2.2822 | 6.62 | 0.250 | −8.78 | −18.91 | −9.73 |
| 2215 − 037 | 0.241 | RQQ | −10.50501 | 8.20 | 3.5622 | 7.90 | 0.247 | −10.98 | −21.11 | −11.93 |
| 2344 + 184 | 0.138 | RQQ | −9.37501 | 7.07 | 2.4322 | 6.77 | 0.138 | −8.42 | −18.56 | −9.38 |
9. Conclusions
The growth of accreting supermassive black hole seeds and their neutrino radiation are found to be common phenomena in the AGNs. In this report, we further expose the assertions made in the framework of microscopic theory of black hole via reviewing the mass assembly history of 377 plausible accreting supermassive black hole seeds. After the numerous reiterating integrations of the state equations of SPC-configurations, we compute their intermediate seed masses, , PRTs, initial redshifts, zSeed, and neutrino fluxes. All the results are presented in Tables 1–5. Figure 6 gives the intermediate seed masses versus the present masses MBH/M⊙ of 337 black holes, on logarithmic scales. In accordance, the AGNs are favored as promising pure UHE neutrino sources. Such neutrinos may reveal clues on the puzzle of origin of UHE cosmic rays. We regard the considered black holes only as the potential neutrino sources. The obtained results, however, may suffer and that would be underestimated if not all 377 live black holes in the MBH/M⊙≃1.1 × 106 to 1.3 × 1010 mass range at present reside in final stage of their growth, when the protomatter disk driven by accretion has reached the event horizon.
Conflict of Interests
The author declares that there is no conflict of interests regarding the publication of this paper.
Acknowledgment
The very helpful and knowledgable comments from the anonymous referee which have essentially clarified the paper are much appreciated.
Appendices
A. Outline of the Key Points of Proposed Gravitation Theory at Huge Energies
The proposed gravitation theory explores the most important processes of rearrangement of vacuum state and a spontaneous breaking of gravitation gauge symmetry at huge energies. From its historical development, the efforts in gauge treatment of gravity mainly focus on the quantum gravity and microphysics, with the recent interest, for example, in the theory of the quantum superstring or, in the very early universe, in the inflationary model. The papers on the gauge treatment of gravity provide a unified picture of gravity modified models based on several Lie groups. However, currently no single theory has been uniquely accepted as the convincing gauge theory of gravitation which could lead to a consistent quantum theory of gravity. They have evoked the possibility that the treatment of spacetime might involve non-Riemannian features on the scale of the Planck length. This necessitates the study of dynamical theories involving post-Riemannian geometries. It is well known that the notions of space and connections should be separated; see, for example, [78–81]. The curvature and torsion are in fact properties of a connection, and many different connections are allowed to exist in the same spacetime. Therefore, when considering several connections with different curvature and torsion, one takes spacetime simply as a manifold and connections as additional structures. From this view point in a recent paper [82] we tackle the problem of spacetime deformation. This theory generalizes and, in particular cases, fully recovers the results of the conventional theory. Conceptually and techniquewise this theory is versatile and powerful and manifests its practical and technical virtue in the fact that through a nontrivial choice of explicit form of the world-deformation tensor, which we have at our disposal, in general, we have a way to deform the spacetime which displayed different connections, which may reveal different post-Riemannian spacetime structures as corollary. All the fundamental gravitational structures in fact—the metric as much as the coframes and connections—acquire a spacetime deformation induced theoretical interpretation. There is another line of reasoning which supports the side of this method. We address the theory of teleparallel gravity and construct a consistent Einstein-Cartan (EC) theory with the dynamical torsion. We show that the equations of the standard EC theory, in which the equation defining torsion is the algebraic type and, in fact, no propagation of torsion is allowed, can be equivalently replaced by the set of modified Einstein-Cartan equations in which the torsion, in general, is dynamical. Moreover, the special physical constraint imposed upon the spacetime deformations yields the short-range propagating spin-spin interaction. For the self-contained arguments in Appendix A.1 and Appendices B and C we complete the spacetime deformation theory [82] by new investigation of building up the distortion-complex of spacetime continuum and showing how it restores the world-deformation tensor, which still has been put in by hand. We extend necessary geometrical ideas of spacetime deformation in concise form, without going into the subtleties, as applied to the gravitation theory which underlies the MTBH framework. I have attempted to maintain a balance between being overly detailed and overly schematic. Therefore the text in the appendices should resemble a “hybrid” of a new investigation and some issues of proposed gravitation theory.
A.1. A First Glance at Spacetime Deformation
A.2. General Gauge Principle
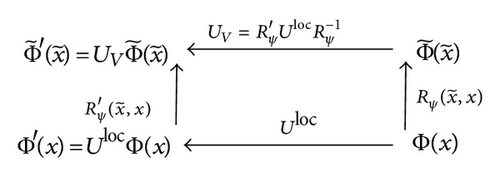
Keeping in mind the aforesaid, we develop the alternative framework of the general gauge principle (GGP), which is the distortion gauge induced fiber-bundle formulation of gravitation. As this principle was in use as a guide in constructing our theory, we briefly discuss its general implications in Appendix D. The interested reader is invited to consult the original paper [74] for details. In this, we restrict ourselves to consider only the simplest spacetime deformation map, (). This theory accounts for the gravitation gauge group GV generated by the hidden local internal symmetry Uloc. We assume that a distortion massless gauge field a(x) (≡an(x)) has to act on the external spacetime groups. This field takes values in the Lie algebra of the abelian group Uloc. We pursue a principle goal of building up the world-deformation tensor, , where F is the differential form of gauge field F = (1/2)Fnmϑn∧ϑm. We connect the structure group GV, further, to the nonlinear realization of the Lie group GD of distortion of extended space (E.1), underlying the M4. This extension appears to be indispensable for such a realization. In using the 6D language, we will be able to make a necessary reduction to the conventional 4D space. The laws guiding this redaction are given in Appendix E. The nonlinear realization technique or the method of phenomenological Lagrangians [85–91] provides a way to determine the transformation properties of fields defined on the quotient space. In accordance, we treat the distortion group GD and its stationary subgroup H = SO(3), respectively, as the dynamical group and its algebraic subgroup. The fundamental field is distortion gauge field (a) and, thus, all the fundamental gravitational structures in fact—the metric as much as the coframes and connections—acquire a distortion-gauge induced theoretical interpretation. We study the geometrical structure of the space of parameters in terms of Cartan’s calculus of exterior forms and derive the Maurer-Cartan structure equations, where the distortion fields (a) are treated as the Goldstone fields.
A.3. A Rearrangement of Vacuum State
A.4. Model Building: Field Equations
B. A Hard Look at Spacetime Deformation
C. Determination of and in Standard Theory of Gravitation
D. The GGP in More Detail
Given the principal fiber bundle with the structure group GV, the local coordinates are , where and UV ∈ GV, the total bundle space is a smooth manifold, and the surjection is a smooth map . A set of open coverings of V4 with satisfy . The collection of matter fields of arbitrary spins take values in standard fiber over . The fibration is given as . The local gauge will be the diffeomorphism map , since maps onto the direct (Cartesian) product . Here represents the fiber product of elements defined over space V4 such that and for all , where is the identity element of the group GV. The fiber at is diffeomorphic to , where is the fiber space, such that . The action of the structure group GV on defines an isomorphism of the Lie algebra of GV onto the Lie algebra of vertical vector fields on tangent to the fiber at each called fundamental. To involve a drastic revision of the role of gauge fields in the physical concept of the spacetime deformation, we generalize the standard gauge scheme by exploring a new special type of distortion gauge field, (a), which is assumed to act on the external spacetime groups. Then, we also consider the principle fiber bundle, P(M4, Uloc; s), with the base space M4, the structure group Uloc, and the surjection s. The matter fields Φ(x) take values in the standard fiber which is the Hilbert vector space where a linear representation U(x) of group Uloc is given. This space can be regarded as the Lie algebra of the group Uloc upon which the Lie algebra acts according to the law of the adjoint representation: a↔ad aΦ → [a, Φ].
E. A Lie Group of Distortion
- (1)
In case of free flat space M6, the subspace T3 is isotropic. And in so far it contributes in line element just only by the square of the moduli t = |x0|, x0 ∈ T3, then, the reduction M6 → M4 = R3 ⊕ T1 can be readily achieved if we use t = |x0| for conventional time.
- (2)
In case of curved space, the reduction V6 → V4 can be achieved if we use the projection () of the temporal component () of basis six-vector on the given universal direction (). By this we choose the time coordinate. Actually, the Lagrangian of physical fields defined on R6 is a function of scalars such that A(λα)B(λα) = AαBα + A0αB0α; then upon the reduction of temporal components of six-vectors we may fulfill a reduction to V4.
F. Field Equations at Spherical Symmetry
G. SPC-Configurations
 -configuration and finally in the
-configuration and finally in the  -configuration. The maximal contribution to the path integral comes from the surface σ0 of the minimum surface area “instanton”. A computation of the transition amplitude is straightforward by summing over all the small vibrations around σ0. In domain ρd ≤ ρ < ρas, one has the string flip-flop regime in presence of ID, at distances 0.25 fm < rNN ≤ 0.4 fm. That is, the system is made of quark protomatter in complete β-equilibrium with rearrangement of string connections joining them. In final domain ρ > ρas, the system is made of quarks in one bag in complete β-equilibrium at presence of ID. The quarks are under the weak interactions and gluons, including the effects of QCD-perturbative interactions. The QCD vacuum has a complicated structure, which is intimately connected to the gluon-gluon interaction. In most applications, sufficient accuracy is obtained by assuming that all the quarks are almost massless inside a bag. The latter is regarded as noninteracting Fermi gas found in the ID-region of the space-time continuum, at short distances rNN ≤ 0.25 fm. Each configuration is defined by the two free parameters of central values of particle concentration and dimensionless potential of space-like ID-field x(0). The interior gravitational potential matches the exterior one at the surface of the configuration. The central value of the gravitational potential x0(0) can be found by reiterating integrations when the sewing condition of the interior and exterior potentials holds. The key question of stability of SPC was studied in [72]. In the relativistic case the total mass-energy of SPC is the extremum in equilibrium for all configurations with the same total number of baryons. While the extrema of and N occur at the same point in a one-parameter equilibrium sequence, one can look for the extremum of on equal footing. Minimizing the energy will give the equilibrium configuration, and the second derivative of will give stability information. Recall that, for spherical configurations of matter, instantaneously at rest, small radial deviations from equilibrium are governed by a Sturm-Liouville linear eigenvalue equation [98], with the imposition of suitable boundary conditions on normal modes with time dependence . A necessary and sufficient condition for stability is that the potential energy be positive defined for all initial data of , namely, in first order approximation when one does not take into account the rotation and magnetic field, if the square of frequency of normal mode of small perturbations is positive. A relativity tends to destabilize configurations. However, numerical integrations of the stability equations of SPC [72] give for the pressure-averaged value of the adiabatic index the following values: for the SPCI and for SPCII configurations. This clearly proves the stability of resulting SPC. Note that the SPC is always found inside the event horizon sphere, and therefore it could be observed only in presence of accreting matter.
-configuration. The maximal contribution to the path integral comes from the surface σ0 of the minimum surface area “instanton”. A computation of the transition amplitude is straightforward by summing over all the small vibrations around σ0. In domain ρd ≤ ρ < ρas, one has the string flip-flop regime in presence of ID, at distances 0.25 fm < rNN ≤ 0.4 fm. That is, the system is made of quark protomatter in complete β-equilibrium with rearrangement of string connections joining them. In final domain ρ > ρas, the system is made of quarks in one bag in complete β-equilibrium at presence of ID. The quarks are under the weak interactions and gluons, including the effects of QCD-perturbative interactions. The QCD vacuum has a complicated structure, which is intimately connected to the gluon-gluon interaction. In most applications, sufficient accuracy is obtained by assuming that all the quarks are almost massless inside a bag. The latter is regarded as noninteracting Fermi gas found in the ID-region of the space-time continuum, at short distances rNN ≤ 0.25 fm. Each configuration is defined by the two free parameters of central values of particle concentration and dimensionless potential of space-like ID-field x(0). The interior gravitational potential matches the exterior one at the surface of the configuration. The central value of the gravitational potential x0(0) can be found by reiterating integrations when the sewing condition of the interior and exterior potentials holds. The key question of stability of SPC was studied in [72]. In the relativistic case the total mass-energy of SPC is the extremum in equilibrium for all configurations with the same total number of baryons. While the extrema of and N occur at the same point in a one-parameter equilibrium sequence, one can look for the extremum of on equal footing. Minimizing the energy will give the equilibrium configuration, and the second derivative of will give stability information. Recall that, for spherical configurations of matter, instantaneously at rest, small radial deviations from equilibrium are governed by a Sturm-Liouville linear eigenvalue equation [98], with the imposition of suitable boundary conditions on normal modes with time dependence . A necessary and sufficient condition for stability is that the potential energy be positive defined for all initial data of , namely, in first order approximation when one does not take into account the rotation and magnetic field, if the square of frequency of normal mode of small perturbations is positive. A relativity tends to destabilize configurations. However, numerical integrations of the stability equations of SPC [72] give for the pressure-averaged value of the adiabatic index the following values: for the SPCI and for SPCII configurations. This clearly proves the stability of resulting SPC. Note that the SPC is always found inside the event horizon sphere, and therefore it could be observed only in presence of accreting matter.



