Clustering coefficient is a very important measurement in complex networks, and it describes the average ratio between the actual existent edges and probable existent edges in the neighbor of one vertex in a complex network. Besides, in a complex networks, the dynamic change of edges can trigger directly the evolution of network and further affect the clustering coefficients. As a result, in this paper, we investigate the effects of the dynamic change of edge on the clustering coefficients. It is illustrated that the increase and decrease of the clustering coefficient can be effectively controlled by adding or deleting several edges of the network in the evolution of complex networks.

1. Introduction

Clustering coefficient is one of the most important quantities in complex networks which can depict the average number of the ratio of the actual existence sides of the neighbors of the point and the sides that may exist in the neighbors of the point in the complex networks. At present, there are two different but the most basic definitions of clustering coefficients. Firstly, Watts and Strogatz proposed the concept of the clustering coefficients in their creative small-world network model which is denoted by C [1]. Secondly, shortly after Watts and Strogatz proposed the clustering coefficients, Newman et al. defined a concept similar to the former “transitivity,” which is denoted by C^∗ [2].

Although the clustering coefficients is widely used in the study of complex networks, scholars do not have clustering coefficients discontinuous [3–19]. Shi et al. made a good overview on the research in this area and proposed a general method of calculating the clustering coefficients [20]. Soffer and Vazquez proposed a definition of clustering coefficients independent of degree [21].

In the complex networks, dynamic change of the edges directly led to the dynamic evolution of the network and thus affect the variation of the clustering coefficients. And one of the core features of complex networks is a huge number of nodes and edges. This feature directly affects the complexity of calculating the clustering coefficient. In this paper, how dynamical changes of the edges affect the clustering coefficient is deeply presented which can reveal the impact of changes of the edge in the quality and quantity on the clustering coefficients. In addition, the obtained results show that, in the evolution of complex networks, we can make the clustering coefficients increase or decrease by deleting or adding the certain edges of networks.

2. Basic Concepts

For a given complex network, A = (a_ij) denotes the adjacency matrix of the network, |V| denotes the number of nodes in the network, k(r) denotes the degree of node r, N_G(r) denotes the set of neighbors of node r, E(r) denotes the number of edges in the neighbors N_G(r) of node r, and C(r) denotes the clustering coefficient of node r; namely,

(1)

with global clustering coefficient:

(2)

As a special case, if k(r) = 1 (r = 1,2, …, |V|), then C(r) = 1.

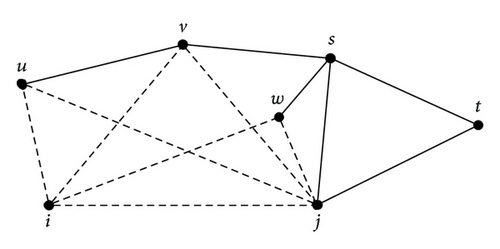
For sake of description, we define a set △_(i,j) = {r∣a_ija_ria_rj = 1} by the adjacency matrix A = (a_ij) _|V|×|V| of the network. The set is used to describe a set of triangles with a shared edge e_ij. And we use the |△|_(i,j) to denote the number of these triangles. In fact, when the edge e_ij exists, |△|_(i,j) is equal to the number of nodes in N_G(i)∩N_G(j). We show an example in Figure 1.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

The dashed line represents the triangles with a shared edge e_ij and |△|_(i,j) = 3.

3. Effect of Edge Changes on the Clustering Coefficients

3.1. Effect of Deleting an Edge on the Clustering Coefficients

In this paper, we do not consider deleting the associated edge of suspension node. One edge e_ij of network is deleted, k(i), k(j), N_G(i), and N_G(j) will certainly change, and |△|_i,j may change. These factors that are intertwined directly affect the change of C(i), C(j) and then affect the change of the complex network clustering coefficient C.

Case 1 (k(i) ≥ 3 and k(j) ≥ 3). (1) After the edge e_ij is deleted, the triangles that contained the shared edge e_ij turn to trielements because of losing side e_ij, but k(r) (r ∈ △_(i,j)) does not change. As a result, the changing amount of C(r) (r ∈ △_(i,j)) is

(3)

(2) N_G(i) turns to , . k(i) turns to k^′(i) = k(i) − 1. In addition, the triangles which contained the shared edge e_ij turn to trimer because of losing side e_ij. Therefore, the number of the edges of neighbors of node i reduces |△|_i,j, C(i) turns to C^′(i), and the amount of change is denoted by △C(i). As a result, we have the following expressions:

(4)

Similarly, C(j) turns to C^′(j), and the amount of change is denoted by △C(j) with

(5)

As mentioned above, when e_ij is a edge of the complex networks with k(i)⩾3 and k(j)⩾3, deleting edge e_ij will lead to the change amount of the network clustering coefficient C which is denoted by △C:

(6)

Case 2 (k(i) = 2 and k(j)⩾3). Consider the following:

(7)

Case 3 (k(i) ≥ 3 and k(j) = 2). Consider the following:

(8)

Case 4 (k(i) = 2 and k(j) = 2). Consider the following:

(9)

3.2. Effect of Adding an Edge on the Clustering Coefficients

If edge e_ij is added, clustering coefficient C(r) (r ∈ △_(i,j)), C(i), and C(j) will change.

In this case, we just consider k(i) ≥ 2 and k(j) ≥ 2.

(1)
The changing amount of C(r) is as follows:
(10)
(2)
N_G(i) turns into , . k(i) turn into k^′(i) = k(i) + 1. Without loss of generality, we assume that the former trielements turn into triangle because of adding edge e_ij. Therefore, the number of the edges among the neighbors of node i increases |△|_(i,j). The above reasons make C(i) turn into C^′(i) and the changing amount is denoted by △C(i). As a result, we have the following expressions:
(11)

with

(12)

Similarly, C(j) turns into C^′(j), and the changing amount is denoted by △C(j) with

(13)

After adding an edge e_ij into the network, the changing amount of the clustering coefficients C of the network is △C with

(14)

From the above analysis, one can see that, by adding or deleting an edge in the complex networks, the clustering coefficients of the complex networks may change. If we continue in-depth to analysis the above conclusions under the premise without destroying network connectivity, the following conclusions can be clearly gained.

Theorem 1. Deleting (adding) the edge e_ij does not constitute a triangle with any nodes in the network, and the clustering coefficient of the network increases (decreases).

Proof. If the edge e_ij does not constitute a triangle with any nodes in the network, then

(15)

Based on the above analysis, if k(i) = 2, then △C(i) = C^′(i) − C(i) = 1 − 0 = 1; if k(i) ≥ 3, then △C(i) = C^′(i) − C(i) = 2C(i)[|V | (k(i) − 2)] ⁻¹. That is to say that deleting the edge e_ij does not constitute a triangle with any nodes in the network, and the clustering coefficient of the network increases.

Similarly, based on formula (13), adding the edge e_ij does not constitute a triangle with any nodes in the network, and the clustering coefficient of the network decreases.

Theorem 2. If C(i)≥(|△|_{(i, j)}/(k(i) − 1)), then △C(i) ≥ 0 after the edge e_ij was deleted.

Proof. When k(i) = 2, if |△|_(i,j) = 0, by Theorem 1, △C(i) ≥ 0; if |△|_(i,j) = 1, after the edge e_ij was deleted, C(i) = 1, △C(i) = C^′(i) − C(i) = 1 − 1 = 0, and △C(i) ≥ 0.

When k(i) ≥ 3,

(16)

Obviously, if C(i) ≥ (|△|_{(i, j)}/(k(i) − 1)), then △C(i) ≥ 0.

Corollary 3. If C(i)<(|△|_{(i, j)}/(k(i) − 1)), then △C(i) ≤ 0 if edge e_ij is deleted.

If C(i)<(|△|_{(i, j)}/(k(i) − 1)), then |△|_(i,j) ≠ 0 or k(i) = 1 (do not consider this case). When |△|_(i,j) ≠ 0, as k(i) = 2, after the edge e_ij was deleted, △C(i) ≥ 0.

It is obtained directly from formula (13).

Corollary 4. If C(i)>(|△|_{(i, j)}/(k(i) − 1)), then △C(i) < 0 if the edge e_ij is added.

4. Discussion and Conclusion

In this paper, we present a systematic study on the effects of dynamic change of edges on clustering coefficients. It was found that the increase and decrease of the clustering coefficient can be effectively characterized by adding or deleting some edges of the network in the evolution of complex networks.

For the adaptive network, the susceptible may keep away from the infective for the reason that the susceptible individuals have the ability to recognize the infective group and avoid connecting with them [22]. In this case, the susceptible will delete or add some edges in the complex networks. That is to say that our results can be extended to the disease transmission on complex networks [23–25].

Conflict of Interests

The authors declare that there is no conflict of interests regarding the publication of this paper.

References

1 Watts D. J. and Strogatz S. H., Collective dynamics of ′small-world′ networks, Nature. (1998) 393, no. 6684, 440–442, https://doi.org/10.1038/30918, 2-s2.0-0032482432.
10.1038/30918
CAS PubMed Web of Science® Google Scholar
2 Newman M. E. J., Strogatz S. H., and Watts D. J., Random graphs with arbitrary degree distributions and their applications, Physical Review E: Statistical, Nonlinear, and Soft Matter Physics. (2001) 64, no. 2, 026118, 2-s2.0-0035420732.
10.1103/PhysRevE.64.026118
CAS PubMed Web of Science® Google Scholar
3 Schank T. and Wagner D., Approximating clustering coefficient and transitivity, Journal of Graph Algorithms and Applications. (2005) 9, no. 2, 265–275, https://doi.org/10.7155/jgaa.00108, MR2185281, 2-s2.0-27844434308.
10.7155/jgaa.00108
Google Scholar
4 Barrat A. and Weigt M., On the properties of small-world network models, European Physical Journal B. (2000) 13, no. 3, 547–560, https://doi.org/10.1007/s100510050067, 2-s2.0-0042527883.
10.1007/s100510050067
CAS Web of Science® Google Scholar
5 Albert R. and Barabasi A.-L., Statistical mechanics of complex networks, Reviews of Modern Physics. (2002) 74, no. 1, 47–97, https://doi.org/10.1103/RevModPhys.74.47, MR1895096.
10.1103/RevModPhys.74.47
CAS PubMed Web of Science® Google Scholar
6 Klemm K. and Eguíluz V. M., Growing scale-free networks with small-world behavior, Physical Review E. (2002) 65, no. 5, 057102, https://doi.org/10.1103/PhysRevE.65.057102, 2-s2.0-41349086001.
10.1103/PhysRevE.65.057102
PubMed Web of Science® Google Scholar
7 Fronczak A., Fronczak P., and Holyst J. A., Mean-field theory for clustering coefficients in Barabási-Albert networks, Physical Review E: Statistical, Nonlinear, and Soft Matter Physics. (2003) 68, no. 4, 046126, 2-s2.0-0346935008.
10.1103/PhysRevE.68.046126
CAS PubMed Web of Science® Google Scholar
8 Boguna M. and Pastor-Satorras R., Class of correlated random networks with hidden variables, Physical Review E. (2003) 68, no. 3, 036112, 2-s2.0-0242663620.
10.1103/PhysRevE.68.036112
Web of Science® Google Scholar
9 Newman M. E. J. and Park J., Why social networks are different from other types of networks, Physical Review E: Statistical, Nonlinear, and Soft Matter Physics. (2003) 68, no. 3, 9, 036122, 2-s2.0-0242663598.
10.1103/PhysRevE.68.036122
CAS PubMed Web of Science® Google Scholar
10 Gleiss P. M., Stadler P. F., Wagner A., and Fell D. A., Relevant cycles in chemical reaction networks, Advances in Complex Systems. (2001) 4, no. 2-3, 207–226, https://doi.org/10.1142/S0219525901000140, MR1873758.
10.1142/S0219525901000140
Google Scholar
11 Bianconi G. and Capocci A., Number of loops of size h in growing scale-free networks, Physical Review Letters. (2003) 90, no. 7, 078701, 2-s2.0-0142013808.
10.1103/PhysRevLett.90.078701
PubMed Web of Science® Google Scholar
12 Bollobás B. and Riordan O. M., S. Bornholdt and H. G. Schuster, Mathematical results on scale-free random graphs, Handbook of Graphs and Networks, 2002, 1, Wiley-VCH, Weinheim, Germany, 1–34, MR2016117.
10.1002/3527602755.ch1
Google Scholar
13 Newman M. E. J., The structure and function of complex networks, SIAM Review. (2003) 45, no. 2, 167–256, https://doi.org/10.1137/S003614450342480, MR2010377, 2-s2.0-0038718854.
10.1137/S003614450342480
Web of Science® Google Scholar
14 Dorogovtsev S. N., Goltsev A. V., and Mendes J. F. F., Pseudofractal scale-free web, Physical Review E. (2002) 65, no. 6, 066122, https://doi.org/10.1103/PhysRevE.65.066122, 2-s2.0-41349104020.
10.1103/PhysRevE.65.066122
CAS PubMed Web of Science® Google Scholar
15 Liu Z., Lai Y.-C., Ye N., and Dasgupta P., Connectivity distribution and attack tolerance of general networks with both preferential and random attachments, Physics Letters Section A. (2002) 303, no. 5-6, 337–344, https://doi.org/10.1016/S0375-9601(02)01317-8, 2-s2.0-0037190752.
10.1016/S0375-9601(02)01317-8
CAS Web of Science® Google Scholar
16 Dorogovtsev S. N., Mendes J. F. F., and Samukhin A. N., Structure of growing networks with preferential linking, Physical Review Letters. (2000) 85, no. 21, 4633–4636, https://doi.org/10.1103/PhysRevLett.85.4633, 2-s2.0-0034310713.
10.1103/PhysRevLett.85.4633
CAS PubMed Web of Science® Google Scholar
17 Dorogovtsev S. N. and Mendes J. F. F., Scaling properties of scale-free evolving networks: continuous approach, Physical Review E. (2001) 63, no. 5, 056125, 2-s2.0-0035334069.
10.1103/PhysRevE.63.056125
CAS PubMed Web of Science® Google Scholar
18 Shi D., Chen Q., and Liu L., Markov chain-based numerical method for degree distributions of growing networks, Physical Review E: Statistical, Nonlinear, and Soft Matter Physics. (2005) 71, no. 3, 036140, https://doi.org/10.1103/PhysRevE.71.036140, 2-s2.0-41349086812.
10.1103/PhysRevE.71.036140
PubMed Web of Science® Google Scholar
19 Krapivsky P. L. and Rendner S., Network growth by copying, Physical Review E. (2005) 71, 036118, https://doi.org/10.1103/PhysRevE.71.036118.
10.1103/PhysRevE.71.036118
CAS PubMed Web of Science® Google Scholar
20 Shi D., Zhu S. X., and Liu L., Clustering coefficients of growing networks, Physica A. (2007) 381, no. 1-2, 515–524, https://doi.org/10.1016/j.physa.2007.03.054, 2-s2.0-34249654092.
10.1016/j.physa.2007.03.054
Web of Science® Google Scholar
21 Soffer S. N. and Vazquez A., Network clustering coefficient without degree-correlation biases, Physical Review E. (2005) 71, no. 5, 057101, https://doi.org/10.1103/PhysRevE.71.057101.
10.1103/PhysRevE.71.057101
CAS PubMed Web of Science® Google Scholar
22 Gross T., D′Lima C. J. D., and Blasius B., Epidemic dynamics on an adaptive network, Physical Review Letters. (2006) 96, no. 20, 208701, https://doi.org/10.1103/PhysRevLett.96.208701, 2-s2.0-33646855384.
10.1103/PhysRevLett.96.208701
CAS PubMed Web of Science® Google Scholar
23 Zhang X., Sun G.-Q., Zhu Y.-X., Ma J., and Jin Z., Epidemic dynamics on semi-directed complex networks, Mathematical Biosciences. (2013) 246, no. 2, 242–251, https://doi.org/10.1016/j.mbs.2013.10.001, MR3132045, ZBL1283.92056, 2-s2.0-84888020832.
10.1016/j.mbs.2013.10.001
PubMed Web of Science® Google Scholar
24 Sun G.-Q., Jin Z., Song L.-P., Chakraborty A., and Li B.-L., Phase transition in spatial epidemics using cellular automata with noise, Ecological Research. (2011) 26, no. 2, 333–340, https://doi.org/10.1007/s11284-010-0789-9, 2-s2.0-79952753894.
10.1007/s11284-010-0789-9
Web of Science® Google Scholar
25 Sun G.-Q., Liu Q.-X., Jin Z., Chakraborty A., and Li B.-L., Influence of infection rate and migration on extinction of disease in spatial epidemics, Journal of Theoretical Biology. (2010) 264, no. 1, 95–103, https://doi.org/10.1016/j.jtbi.2010.01.006, MR2981502, 2-s2.0-77649232218.
10.1016/j.jtbi.2010.01.006
PubMed Web of Science® Google Scholar

Citing Literature

All articles

Influence of Dynamical Change of Edges on Clustering Coefficients

Abstract

1. Introduction

2. Basic Concepts

3. Effect of Edge Changes on the Clustering Coefficients

3.1. Effect of Deleting an Edge on the Clustering Coefficients

3.2. Effect of Adding an Edge on the Clustering Coefficients

4. Discussion and Conclusion

Conflict of Interests

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Influence of Dynamical Change of Edges on Clustering Coefficients

Abstract

1. Introduction

2. Basic Concepts

3. Effect of Edge Changes on the Clustering Coefficients

3.1. Effect of Deleting an Edge on the Clustering Coefficients

3.2. Effect of Adding an Edge on the Clustering Coefficients

4. Discussion and Conclusion

Conflict of Interests

References

Citing Literature

Figures

References

Related

Information