Equilibrium Positions for UAV Flight by Dynamic Soaring

1. Introduction

Long endurance flight is a key design criterion for unmanned aerial vehicle [1]. The UAVs’ flight endurance can be improved by the progress in power capacity and aerodynamic and engine design [2], but not all such means are equal. Another important alternative for enhancing UAV flight endurance is to seek energy from flight environment. In nature, there are many large-sized birds which make use of environment energy to enhance their flight ability, such as wandering albatross who extracts energy from horizontally moving air and transfers energy to itself. The achieved energy enables wandering albatrosses to fly continuously without flapping their wings [3, 4]. The flight manoeuvre that wandering albatross performs is referred to as dynamic soaring [5]. Early in 1883, Lord Rayleigh published “The Soaring of Birds” in Nature [6], which is regarded as the first paper about dynamic soaring. Dynamic soaring is possible when there is horizontally moving air in the flight environment. Horizontally moving air is also called gradient wind, in which wind speed varies with altitude. In this paper, both the size of the wandering albatrosses with its 3.3 m wing span and its flight performance are taken as a reference model against the dynamic soaring performance of a small UAV.

Dynamic soaring is an important flight technique designed to allow aircraft to extract energy from atmosphere. Based on Lord Rayleigh’s observations of albatrosses in the south Atlantic, more recent publications are concerned with wind estimated and dynamic soaring mechanism. In order to estimate wind field for autonomous dynamic soaring, Lawrance et al. [7, 8] provided a method for taking direct observations of the wind during flight and creating a wind to direct future exploration. The wind estimation is the precondition for dynamic soaring. In this paper, a mathematical model is built for the wind field. As for dynamic soaring mechanism, Grenestedt [9] provided insight into how and where energy is extracted from the wind during dynamic soaring. The effects of some aircraft parameters such as mass, drag area, and wing span were discussed. Bower [5] studied the energy transfer mechanisms for a vehicle flying in a spatially and temporally varying wind field. Deittert et al. [10] investigated optimal trajectories for minimal and maximal wind conditions, and the likelihood of favorable winds was predicted based on long-term weather statics and knowledge of minimal and maximal permissible wind strengths. Cone [11] analyzed the dynamic soaring flight of albatross with mathematical models. Peter [12] draw a conclusion that, in an energy neutral cycle of dynamic soaring, whether the vehicle returns to initial velocity and height with no power input depends only upon the maximum lift-to-drag ratio of the vehicle and the wind speed variation.

Scores of research findings reveal the significant meaning of dynamic soaring. Based on the achievements of these findings, some new ideas are studied in this paper. The authors first extend the idea of Grenestedt [9] by investigating the equilibrium position of dynamic soaring and providing insight into energy variation in equilibrium position. The same as other flight styles, they applied forces on the aircraft for dynamic soaring varying continuously. Then there should be some positions of forces balance in the course of flight. At these points, the aircraft stays in a certain speed, with no kinetic energy loss. Of course, if all the points could chain a closed route, the permanent flying would come true when the aircraft flies along the route.

The rest of the paper is organized as follows: the methodology is described in Section 2, including the wind gradient and the mathematical models for the UAV. Section 3 is simulation results and associated discussion. Finally, the concluding remarks are made in Section 4.

2. Mathematical Formulations of the Problem

Inspired by the forces analysis methods in dynamic soaring suggested by Bower [5] and Deittert et al. [10], the problem of equilibrium position for dynamic soaring is analyzed intensively in this paper. The parameters that can influence the equilibrium position include the range of airspeed, the size of wind gradient, and other parameters. Meanwhile, the maximum value of energy acquired in the equilibrium point is analyzed. Once the parameters of an aircraft are known, the wind gradient suited for the equilibrium position of dynamic soaring can be determined. Similarly, in a known wind field, the type of aircraft that has equilibrium point in dynamic soaring can be found out. A set of computational methods for equilibrium position of dynamic soaring is established. The purpose of this section is to provide a theoretical guidance for the optimal dynamic soaring trajectory by means of the analysis of equilibrium position of dynamic soaring. Due to no kinetic energy loss in the position of forces balance, the mechanical energy increases with increasing value of potential energy of the aircraft in the course of upward flying.

2.1. The Wind Field Model

It is assumed that the aircraft flies over a flat surface and the wind field is steady. There is a horizontal shear flow of the air in the three-dimensional space. The flow of the air causes the wind speed to increase with increasing height above the ground. The air density is assumed to be constant. The wind blows along the negative direction of x-axis, the positive z-axis points to the sky, and the direction of y-axis is dependent on right-handed rule. The relation between wind speed W(z) and height above the surface z is defined as follows [13, 14]:

$$ ()

where W(z) is the wind speed at height z and W_ref is the wind speed at the reference height z_ref. The variable z₀ is the aerodynamic roughness length or the roughness factor. It is an experimentally derived constant that accounts for the kind of surface over which the wind is blowing. Typically, a higher value of the roughness length indicates more obstructions on the surface such as trees and buildings. By differentiating (1) with respect to altitude, the following equation can be obtained:

$$ ()

where G_W is the gradient of the wind field. The variation trends of wind profile and wind gradient profile are depicted in Figure 1.

Figure 1 shows the wind profile and wind gradient profile for value of the roughness coefficient with W_ref = 15 m/s, z_ref = 100 m, and z₀ = 0.05 m.

2.2. Flying Model

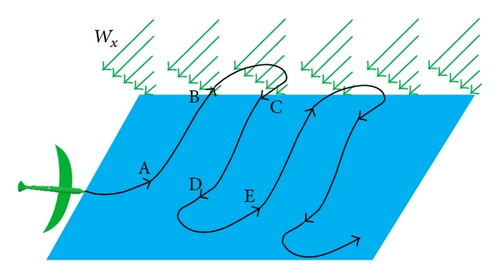
According to the observed data of dynamic soaring [4], the albatross climbs with headwind, and the wind speed increases with the increasing of flight height. After turning in high altitude, the albatross glides with leeward, and the wind speed decreases with the descending of flight height. An illustration of a typical dynamic soaring trajectory is shown in Figure 2.

Compared with Earth fixed frame, the wind relative reference frame of aircraft is not inertial frame in the wind field. So there is an inertial force F_i that works on the aircraft. A noninertial frame is defined, which is the wind relative reference frame of aircraft. In the noninertial frame, there are four applied forces accounted for the aircraft: lift force (L), drag force (D), gravitational force (mg), and inertial force (F_i). The inertial force is created by wind, so the direction of the force is the same as the wind direction. The inertial force can be expressed as [10, 15, 16]

$$ ()

where i is the unit vector of wind field and v_z is the airspeed component in the direction of positive z-axis. So a point mass flight model with attached forces is adopted, and the definitions of forces, speed, and angles used in the model are shown in Figure 3. The UAV is represented by a three-dimensional point-mass model with 3 DOF. From Figure 3, F is the resultant force of lift (L) and drag (D), δ is the angle between F and D, F₁ is the resultant force of gravity (mg) and inertial force (mG_Wv_z), and $$ is the reverse force of F₁. The wind blows in the direction of position X.

The barycenter kinetics equation of aircraft in the noninertial frame is represented as

$$ ()

where $$ is the acceleration vector of airspeed, $$ is the vector of lift, $$ is the vector of drag, and $$ is the vector of gravity. The last expression in (4) is the inertial force.

Using the standard formulations for lift and drag force,

$$ ()

$$ ()

$$ ()

where ρ is air density, S is wing area, C_L is lift coefficient, C_D is drag coefficient, v is the airspeed of the aircraft, C_D0 is the parasitic drag coefficient, and $$ is the induced drag coefficient. Note that

$$ ()

where (L/D)_max is the maximum lift over drag ratio, which, together with C_D0, is the most important aircraft aerodynamic efficiency parameters and fully defines the aerodynamic drag polar.

In the course of flight, the direction of lift is crosscut to drag all the time, so the resultant force (F) of lift and drag can be indicated as

$$ ()

From (9), the airspeed (v) of the aircraft is

$$ ()

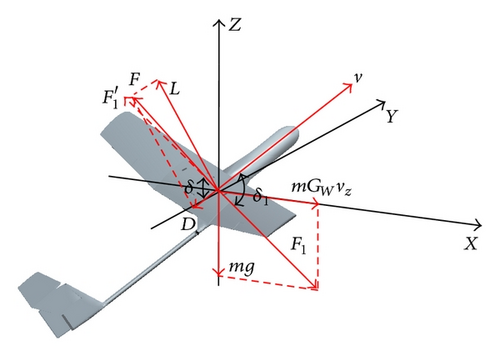
When the value of F is equal to $$, the relationship between v and v_z can be attained by (10).

As for the energy variation, first of all, considering the theorem of kinetic energy in the noninertial frame,

$$ ()

where dE_k is the variation of kinetic energy, dl is the identity element of flight trajectory, and P_D = 1/2ρSC_D. The right-hand side of (11) is infinitesimal energy expressions caused by drag force, inertial force, and gravitational force. The lift force (L) is vertical to the direction of motion, so there is no kinetic energy variation of UAV caused by lift force.

If dl = vdt, dx = v_xdt, and v_x is the airspeed component in the direction of positive x, (11) then transforms into

$$ ()

The integration of (12) can be expressed as

$$ ()

where E_kf is the kinetic energy at height of z_f and E_k0 is the kinetic energy at height of z₀. After the aircraft fly a period of time, if the kinetic energy of aircraft keeps in a constant value, the energy variation of this process could be indicated by the change of altitude difference, and (13) can now be stated to be

$$ ()

Δz is the variation of flight height. From (14), it can be found that the drag (D) and inertial force (F_i) bring about the variation of altitude or the variation of potential energy. That is to say, as long as there was wind gradient (G_W) in the wind field, the aircraft could extract energy from the wind field in the suitable v_x and v_z. In (14), the drag (D) makes negative work all the time, but inertial force (F_i) does positive or negative work to the aircraft, depending on the specific cases. If G_W > 0 and v_zv_x > 0, in this case, inertial force (F_i) does positive work to the aircraft. For the wind field G_W > 0, the following relation must hold:

$$ ()

That is, the aircraft climbs in the positive direction of x-z or dives in the negative direction of x-z; the aircraft extracts energy. If the maneuver is reversed, the aircraft loses energy. The mechanical energy of the aircraft is denoted as E_m. The variation of mechanical energy is equal to the energy caused by drag and inertial force. The identity element of mechanical energy can be expressed as

$$ ()

So the unit mass power of mechanical energy is

$$ ()

where v is the airspeed. Actually, (17) and (14) mean the same things.

3. Simulation Results and Discussions

Because there is no closed form solution for the balance points in dynamic soaring, numerical investigations are carried out instead. As dynamic soaring flight is directly inspired by albatross, wandering albatross’ parameters used by Sachs [4] are assumed. Based on the architecture of a wandering albatross, an aircraft demonstrator model is used as a reference. The UAV demonstrator has similarities in dimension as well as the performances with albatross. This will ensure that the performances of the aircraft model are achievable by an engineering-designed vehicle. The parameter values of albatross and UAV demonstrator are given in Table 1, where E_max⁡ is the maximum lift-to-drag ratio. Compared with the albatross, the UAV demonstrator has a lighter mass. Furthermore, the flying ability close to the ground surface of the UAV demonstrator is limited, while albatross can fly with a wing tip touching the water. For the reason of security, the UAV demonstrator has a smaller wingspan. The aerofoil of UAV demonstrator is E214, which makes the vehicle have a better performance than albatross, reaching a maximum lift-to-drag ratio of 21.

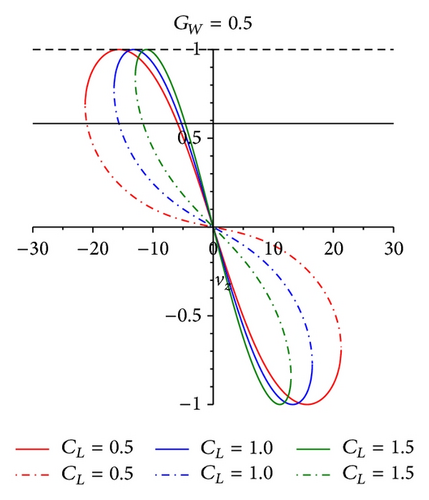
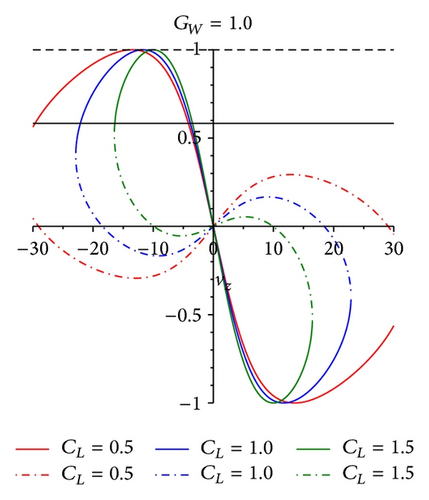
From (26), it can be found that the relationship between variables cos⁡(δ) and cos⁡(ψ) is linear and the value of cos⁡(ψ) is located in the interval [−1,1], so the range of cos⁡(δ) can be defined. The extent of albatross’ v_z and UAV demonstrator’s v_z is shown in Figures 4 and 5, respectively.

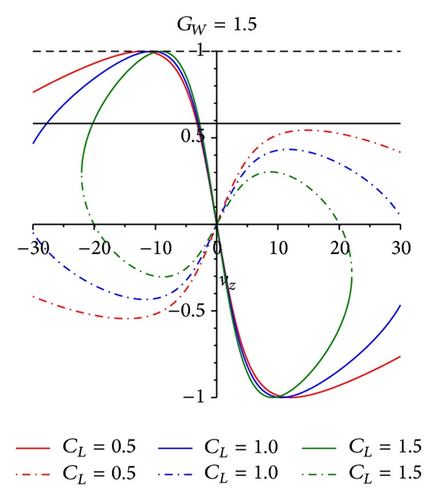
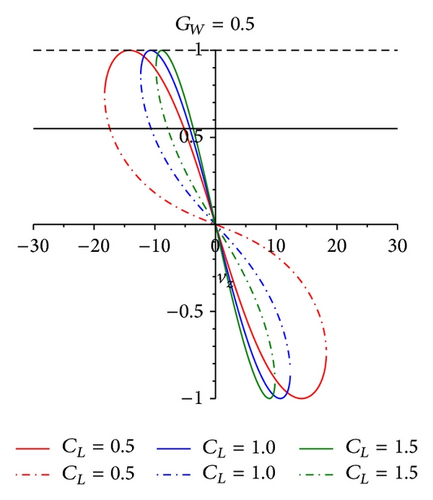
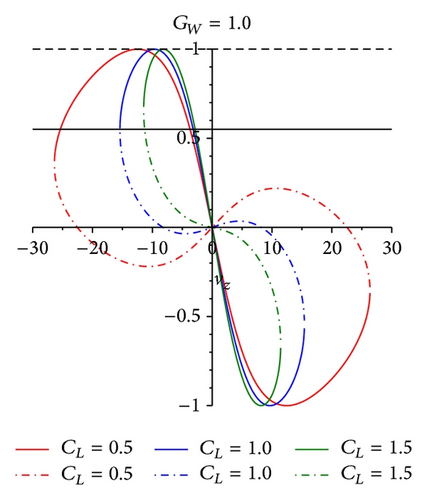
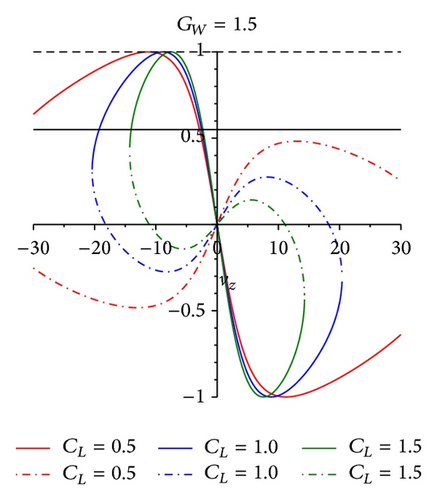
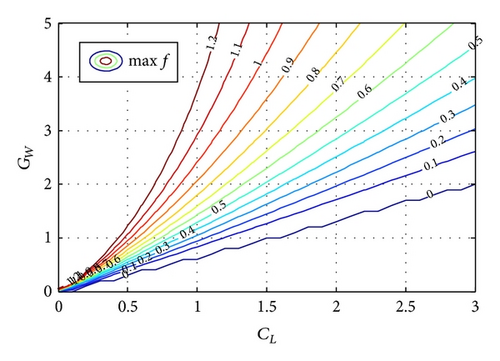
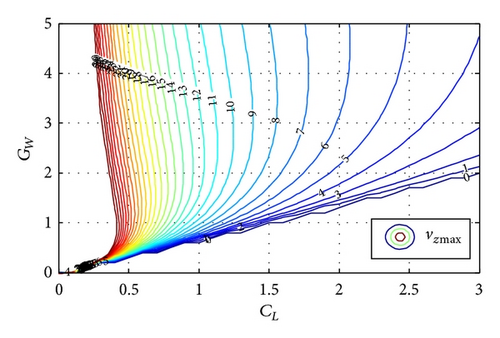
The contour line figure of albatross’ max⁡f and v_z max⁡ is expressed in Figures 6 and 7.

The contour line figure of UAV demonstrator’s max⁡f and v_z max⁡ is expressed in Figures 8 and 9.

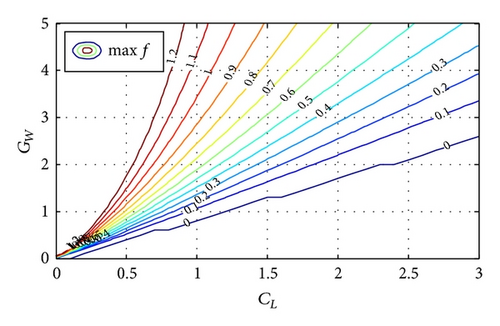
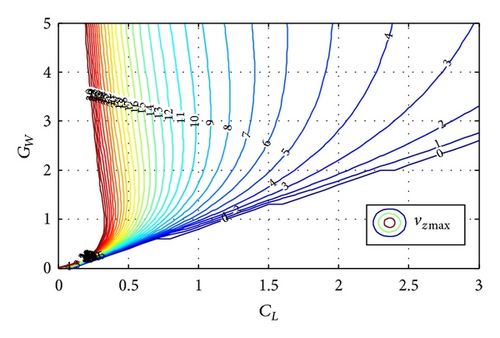
From Figure 6, it is obvious that max⁡f has many values greater than zero. That is to say, (31) has reasonable solutions. From Figure 7, the maximum value of v_z for the albatross’ lifting balance allowance in dynamic soaring can be found. For example, if the lift coefficient of albatross (C_{L albatross}) is 1 and the gradient of the wind field (G_W) is 1, in Figure 6, the value of max⁡f is 0.4. Compared with Figure 7, v_z = 9 m/s; combining with (20), it can be found that v = 17.0 m/s. That is to say, when albatross’ airspeed reaches 17.0 m/s, there exists equilibrium point in this wind field. Just getting the value of airspeed is not enough to make conclusions. The restriction to airspeed is the bank angle of air velocity vector, which is defined as ψ. With the geometrical relationship of forces balanced, one can acquire the space curve of v_x × v_y × v_z, which is obtained by projecting the four-dimensional space v_x × v_y × v_z × ψ into three-dimensional space. The fundamental is to find out a suitable aerodynamic force to compensate the resultant force of gravitation and inertial force. From (24), (25), and (26), the value range of the bank angle is [30°, 60°]. The albatross can reach the equilibrium position in gradient wind under these limiting conditions. Similarly, the equilibrium points for UAV demonstrator in dynamic soaring can be found in Figures 8 and 9.

4. Conclusions

Dynamic soaring gives the albatross an ability to achieve energy from the environment and prolong its flight endurance, which is a guide to consider using dynamic soaring as a propulsive energy source for small UAVs. The paper presents an equilibrium position theory of dynamic soaring which is the forces balance during the flight. At the equilibrium position, the aircraft stays in a certain speed without kinetic energy loss. When the flight direction is upward, the mechanical energy would increase, which can store energy for flight.

In this paper, the wind relative reference frame of aircraft is noninertial, and the inertial force F created by wind can be used to do work for aircraft. In the noninertial frame, the mechanical energy variation of the aircraft equals the energy caused by drag and inertial force. When the wind gradient G_W > 0 and v_zv_x > 0 (v_x, v_z are the airspeed component in the direction of positive x-axis and z-axis), the inertial force (F) does positive work to the aircraft. The mechanical energy variation for unit mass is influenced by wind gradient, mass (m), and drag coefficient.

Because of the existence of the gradient wind field, there are some balance points during dynamic soaring no matter how parameters are chosen. In the contour line figures of albatross’ max⁡f and v_z max⁡, it is easy to find out that the maximum value of v_{z albatross}, lift coefficient (C_{L albatross}), airspeed (v), and bank angle (ψ) and the gradient of the wind field are required by the dynamic soaring balance points. By means of performances comparison between UAV demonstrator and albatross, it is manageable to apply dynamic soaring in engineering practice.

Finally, in order to make dynamic soaring profit from further research work as soon as possible, dynamic soaring experiments are necessary. Furthermore, an investigation with theory of balances for 6 DOF aircraft model would be helpful for instructing the dynamic soaring experiments.

Conflict of Interests

The authors declare that there is no conflict of interests regarding the publication of this paper.