We study a Hopfield-type network that consists of a pair of one-way rings each with three neurons and two-way coupling between the rings. The rings have symmetric group Γ = Z₃ × Z₂, which means the global symmetry Z₂ and internal symmetry Z₃. We discuss the spatiotemporal patterns of bifurcating periodic oscillations by using the symmetric bifurcation theory of delay differential equations combined with representation theory of Lie groups. The existence of multiple branches of bifurcating periodic solution is obtained. We also found that the spatiotemporal patterns of bifurcating periodic oscillations alternate according to the change of the propagation time delay in the coupling; that is, different ranges of delays correspond to different patterns of neural network oscillators. The oscillations of corresponding neurons in the two loops can be in phase, antiphase, T/3, 2T/3, 4T/3, 5T/6, or 7T/6 periods out of phase depending on the delay. Some numerical simulations support our analysis results.

1. Introduction

The theory of spatiotemporal pattern formation in systems of coupled nonlinear oscillators with symmetry has grown extensively in recent years. Its impact has been felt in a wide variety of fields of applied science. Coupled networks of nonlinear dynamical systems have become important models for studying the behavior of large complex systems. These models allow us to investigate fundamental features of physical systems, biological systems, and so on. The central question is to understand how specific properties of the individual behavior and the coupling architecture can give rise to the emergence of new collective phenomena [1–5]. Couple can lead to oscillators’ synchronization, chaos, symmetric bifurcation, and so on [6].

Networks with a ring topology, where locally coupled oscillators or oscillatory populations form a closed loop of signal transmission, appear to be relevant for many practical situations. These systems sometimes show symmetric properties. In general, symmetric systems typically exhibit more complicated bifurcations than nonsymmetric systems, and as well they may increase the dimension of the space and the number of variables involved. Some bifurcations can have a smaller codimension in a class of systems with specified symmetries. Other bifurcations, on the contrary, may not occur in the presence of certain symmetries [7, 8].

Time delays have been incorporated into coupled models by many authors, since in real systems the signal inevitably propagates from one oscillator to the next over a finite distance and with a finite speed; a time delay can not be negligible. From the mathematical point of view, the presence of delays makes the problem harder to handle. In fact, the state vector characterizing a nonlinear delayed system evolves in an infinite dimensional functional space. Networks with interacting loops and time delays are common in physiological systems. For example, there are many interacting loops and feedback systems in the model of brain’s motor circuitry [9, 10].

In this paper, we focus on the simplest Hopfield network with delays. This model consists of two coupling unidirectional rings, each with three oscillators. See Figure 1.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

The architecture of the model (1).

The case leads to the following system of delay differential equations:

()

where τ ≥ 0 is the time delay. Let X = (x₁, x₂, x₃, x₄, x₅, x₆) represent the state variables. For Γ = Z₃ × Z₂, where Z₃ and Z₂ are the cycle group, the action on X follows ρ ∈ Z₃, κ ∈ Z₂:

()

We will determine the effects of symmetric coupling between parallel copies of a network structure in the presence of delays. In the following, we focus on the symmetric properties of (1). Let C([−τ, 0], R⁶) denote the Banach space of continuous mapping from [−τ, 0] to R⁶ equipped with the supremum norm ‖φ‖ = sup⁡_{−τ≤θ≤0} | φ(θ)| for φ ∈ C([−τ, 0], R⁶). Let σ ∈ R, A ≥ 0, X : [σ − τ, σ + A] → R⁶, t ∈ [σ, σ + A] be defined by X_t(θ) = X(t + θ) for −τ ≤ θ ≤ 0. Define the mapping f : C([−τ, 0], R⁶) → R⁶ by

()

where φ ∈ C([−τ, 0], R⁶).

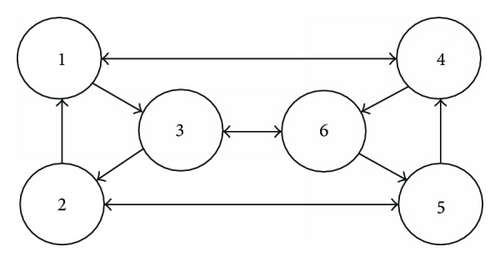
It is clear that (1) has symmetric group Γ = Z₃ × Z₂, which means the global symmetry Z₂ and internal symmetry Z₃.

In the next section we focus on the linear stability analysis of the trivial equilibrium. This then leads us to a discussion of the bifurcations of the trivial equilibrium. In Section 3, we present a characterization of all possible periodic solutions, their twisted isotropy subgroups, and corresponding fixed-point subspaces. We obtain some important results about spontaneous bifurcations of multiple branches of periodic solutions and their spatiotemporal patterns, which describe the oscillatory mode of each neuron. Finally, some numerical simulations are carried out to support the analysis results.

2. Elementary Analysis

It is clear that (0,0,0,0,0,0) is an equilibrium point of (1). The linearization of (1) at the origin leads to

()

The associated characteristic equation of (4) takes the form

()

where

()

Rewrite (4) as

()

with

()

The infinitesimal generator of the C₀-semigroup generated by linear system (4) is

with

()

Regarding τ as the parameter, we determine when the infinitesimal generator A(τ) of the C⁰-semigroup generated by linear system (7) has a pair of pure imaginary eigenvalues.

Using Lemma 2.1 in [11], the characteristic equation then factors as

()

It is not difficult to verify that a + bi is a root of Δ₂ = 0 or Δ₅ = 0 if and only if a − bi is a root of Δ₄ = 0 or Δ₆ = 0.

In order to study the distribution of zeros of (10), it is sufficient to investigate Δ₁ = 0, Δ₂ = 0, Δ₄ = 0, and Δ₅ = 0. We make the following assumption:

(H₁): |b − 1| < c;
(H₂): |1 + (b/2)| < c.

If the assumptions (H₁), (H₂) hold, then the roots of Δ₁ = 0, Δ₂ = 0, Δ₄ = 0, and Δ₅ = 0 have negative real parts when τ = 0. In the sequel, we consider the distribution of zeros of Δ = 0.

Case 1 (Δ1 = 0). Let iω (ω > 0) be a zero of Δ₁; then the critical frequency is identified as

()

and the critical delay is

()

Moreover, we differentiate the equality Δ₁ = 0 with respect to τ to get

()

Next, we consider the generalized eigenspace corresponding to pure imaginary eigenvalues of .

Let assumptions (H₁) and (H₂) hold such that (10) has roots ±iω₁ when . Using Theorem 2.1 in [11], we have the generalized eigenspace consisting of eigenvectors of corresponding to ±iω₁ is

()

where

()

Case 2 (Δ2 = 0). Letting iω (ω ≠ 0) be a zero of Δ₂, then

()

For further analysis, we found that the transversality conditions are met:

()

The generalized eigenspace consisting of eigenvectors of corresponding to is

()

where

()

In a similar manner it can be shown that, for the fourth factor, Δ₄ = 0, and fifth factor, Δ₅ = 0, we have the following.

Case 3 (Δ4 = 0). In this case,

()

and the transversality conditions are also met:

()

The generalized eigenspace

consisting of eigenvectors of

corresponding to ±iω₄ is

()

where

()

Case 4 (Δ5 = 0). Using the same method of case two, we have

()

where

()

3. Multiple Hopf Bifurcations

In order to study the Hopf bifurcation of the origin, we consider the action of Γ × S¹, where Γ = Z₂ × Z₃ and S¹ is the temporal. The action of the group S¹ is defined as follows:

()

where θ ∈ S¹. It is clear that

()

For fixed k, j, let T = 2π/ω_±. Denote by P_T the Banach space of all continuous T-periodic solutions. Then Γ × S¹ acts on P_T by

()

Denote by SP_T the subspace of P_T consisting of all T-periodic solutions of (4) with

. Then, for each subgroup Σ ≤ Γ × S¹,

()

is a subspace.

In the following, by discussing the isotropy subgroup and fixed-point subspaces, we will give the possible bifurcating solutions. From Section 2, we have obtained the generalized eigenspace corresponding to pure imaginary eigenvalues of . Hence, we know their corresponding isotropy subgroup; see Table 1.

Table 1. The twisted isotropy subgroups for Γ-equivariant system (1).

τ	Group action	Twisted isotropy subgroups	Fixed-point subspaces
		∑ (ρ, κ)	ς₁(θ), ς₂(θ)

			ε₁(θ), ε₂(θ), ε₃(θ), ε₄(θ).

		∑ (ρ, −κ)	ς₃(θ), ς₄(θ)

			ϵ₁(θ), ϵ₂(θ), ϵ₃(θ), ϵ₄(θ)

The equivariant bifurcation theorem asserts the existence of branches of small amplitude periodic solutions to system (1), whose spatiotemporal symmetries can be completely characterized by isotropy subgroup.

In case one, Δ₁ = 0 implies that the purely imaginary eigenvalues associated with Hopf bifurcation are simple. It follows that the action of Z₂ × Z₃ × S¹ is given by ρz = z; κz = z. Obviously, the maximal isotropy subgroup is Z₂ × Z₃, which corresponds to standard Hopf bifurcation and is preserved. Thus, all neurons in two rings are synchronous:

(1)
(x(t), x(t), x(t), x(t), x(t), x(t)).

Similar to the analysis in Case 2, Δ₂ = 0 implies that the purely imaginary eigenvalues associated with Hopf bifurcation are double. ∑ (ρe^i2π/3, κ) and ∑ (ρe^i4π/3, κ) are maximal isotropy subgroups of Z₂ × Z₃ which are generated by ρz = e^i2π/3z; κz = z and ρz = e^i4π/3z; κz = z. Two types of symmetric periodic solutions are generated:

(2)
(x(t), x(t + (T/3)), x(t + (2T/3)), x(t), x(t + (T/3)), x(t(2T/3)));
(3)
(x(t), x(t + (2T/3)), x(t + (4T/3)), x(t), x(t + (2T/3)), x(t(4T/3))).

For Case 3, Δ₄ = 0 means the purely imaginary eigenvalues associated with Hopf bifurcation are simple, and the maximal isotropy subgroup is ∑ (ρ, −κ) and the symmetric periodic solutions have the form

(4)
(x(t), x(t), x(t), −x(t), −x(t), −x(t)).

That means neurons in different rings are T/2 out of phase with each other, and all neurons are 2T/3 out of phase with the adjacent behaving identically in the same ring.

The fourth case, Δ₅ = 0, gives purely imaginary with double. The maximal isotropy subgroup has two types: ∑ (ρe^i2π/3, −κ) and ∑ (ρe^i4π/3, −κ), so the symmetric periodic solutions have the form

(5)
(x(t), x(t + (T/3)), x(t + (2T/3)), x(t + (T/2)), x(t + (5T/6)), x(t(7T/6)));
(6)
(x(t), x(t + (2T/3)), x(t + (T/3)), x(t + (T/2)), x(t + (7T/6)), x(t + (5T/6))).

In summary, we write the results in Table 2.

Table 2. Bifurcating periodic solutions.

Twisted isotropy subgroups ∑	Periodic solutions
∑ (ρ, κ)	(x(t), x(t), x(t), x(t), x(t), x(t))

∑ (ρe^i2π/3, κ)

∑ (ρe^i4π/3, κ)

∑ (ρ, −κ)	(x(t), x(t), x(t), −x(t), −x(t), −x(t))

∑ (ρe^i2π/3, −κ)

∑ (ρe^i4π/3, −κ)

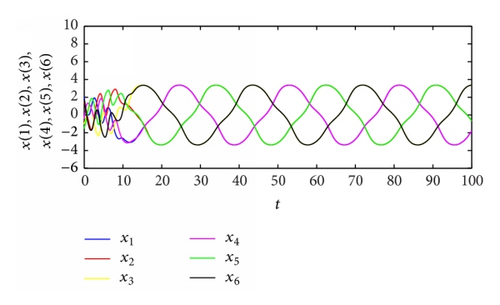
4. Computer Simulation

To illustrate the analytical results found, in the following we consider the following particular case of (1).

Let b = −0.5, c = 2. Then , .

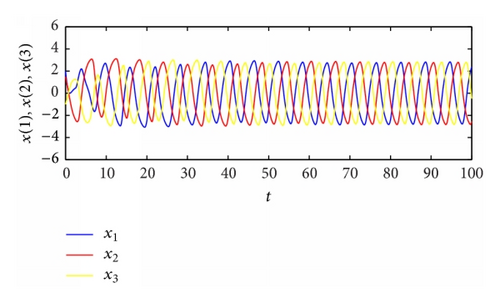
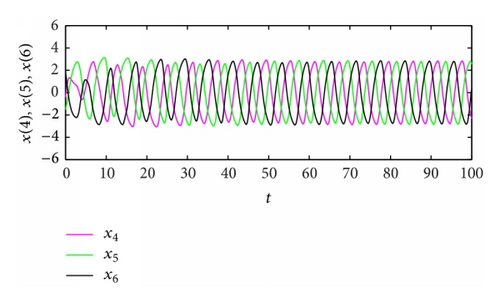
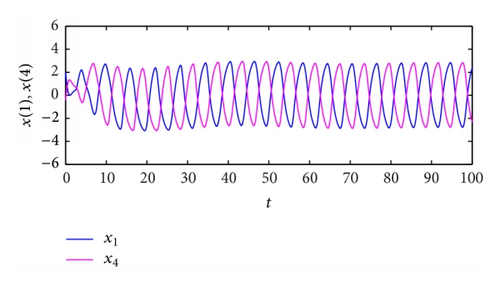
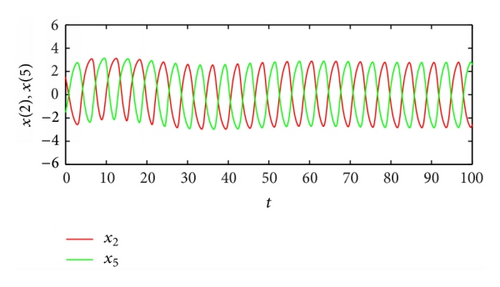
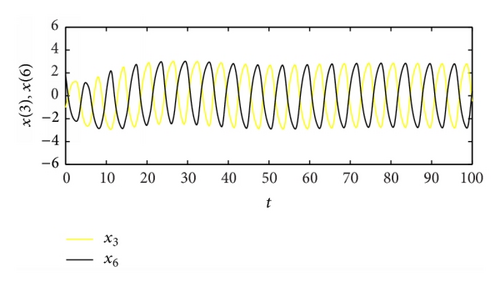
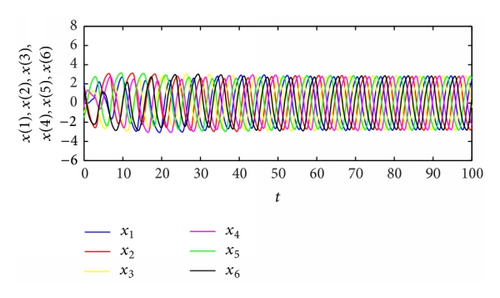
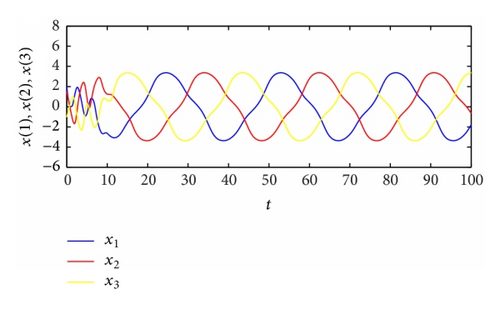
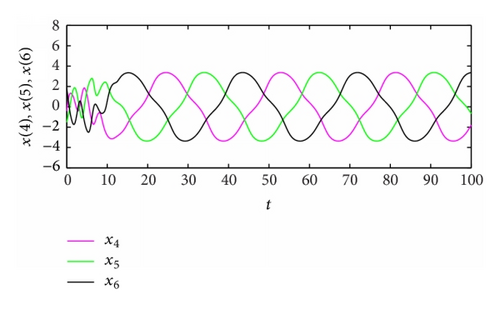
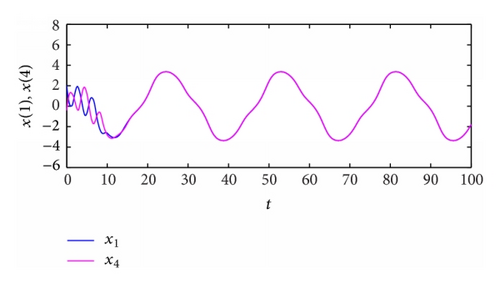
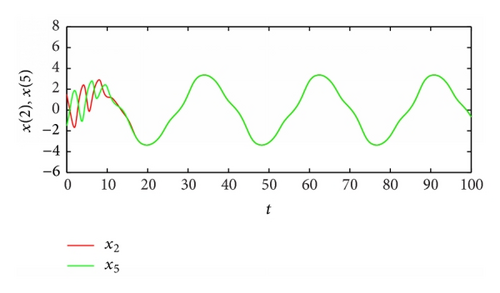
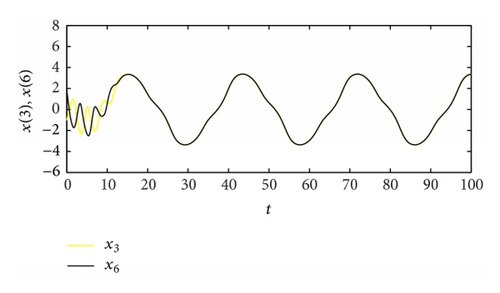
From Table 2, the spatiotemporal patterns of bifurcating periodic oscillations alternate according to the change of the propagation time delay. See Figures 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, and 13.

Conflict of Interests

The authors declare that there is no conflict of interests regarding the publication of this paper.

References

1 Dias A. P. S. and Lamb J. S. W., Local bifurcation in symmetric coupled cell networks: linear theory, Physica D: Nonlinear Phenomena. (2006) 223, no. 1, 93–108, https://doi.org/10.1016/j.physd.2006.08.014, 2-s2.0-33750077831.
10.1016/j.physd.2006.08.014
Web of Science® Google Scholar
2 Perlikowski P., Yanchuk S., Popovych O. V., and Tass P. A., Periodic patterns in a ring of delay-coupled oscillators, Physical Review E: Statistical, Nonlinear, and Soft Matter Physics. (2010) 82, no. 3, 036208, https://doi.org/10.1103/physreve.82.036208, 2-s2.0-78650713506.
10.1103/PhysRevE.82.036208
CAS PubMed Web of Science® Google Scholar
3 Bonnin M., Waves and patterns in ring lattices with delays, Physica D: Nonlinear Phenomena. (2009) 238, no. 1, 77–87, https://doi.org/10.1016/j.physd.2008.08.015, 2-s2.0-56349144131.
10.1016/j.physd.2008.08.015
Web of Science® Google Scholar
4 Zhang P., Guo S., and He Y., Dynamics of a delayed two-coupled oscillator with excitatory-to-excitatory connection, Applied Mathematics and Computation. (2010) 216, no. 2, 631–646, https://doi.org/10.1016/j.amc.2010.01.097, 2-s2.0-77649236542.
10.1016/j.amc.2010.01.097
Web of Science® Google Scholar
5 Zhang C., Zheng B., and Wang L., Multiple Hopf bifurcations of three coupled van der Pol oscillators with delay, Applied Mathematics and Computation. (2011) 217, no. 17, 7155–7166, https://doi.org/10.1016/j.amc.2011.01.110, 2-s2.0-79952757621.
10.1016/j.amc.2011.01.110
Web of Science® Google Scholar
6 Drubi F., Ibáñez S., and Rodríguez J. Á., Coupling leads to chaos, Journal of Differential Equations. (2007) 239, no. 2, 371–385, https://doi.org/10.1016/j.jde.2007.05.024, 2-s2.0-34447265301.
10.1016/j.jde.2007.05.024
Web of Science® Google Scholar
7 Golubitsky M., Stewart I. N., and Schaeffer D. G., Singularities and Groups in Bifurcation Theory: Vol. 7, 1988, 69, Springer, New York, NY, USA, Applied Mathematical Sciences.
10.1007/978-1-4612-4574-2
Google Scholar
8 Yuri A. K., Elements of Applied Bifurcation Theory, 1995, Springer, New York, NY, USA.
Google Scholar
9 Guo S. and Man J., Patterns in hierarchical networks of neuronal oscillators with D3 × Z3 symmetry, Journal of Differential Equations. (2013) 254, no. 8, 3501–3529, https://doi.org/10.1016/j.jde.2013.01.027, 2-s2.0-84874229207.
10.1016/j.jde.2013.01.027
Web of Science® Google Scholar
10 Campbell S. A., Edwards R., and van den Driessche P., Delayed coupling between two neural network loops, SIAM Journal on Applied Mathematics. (2005) 65, no. 1, 316–335, https://doi.org/10.1137/s0036139903434833, 2-s2.0-16244385615.
10.1137/S0036139903434833
Web of Science® Google Scholar
11 Zhang C., Zhang Y., and Zheng B., A model in a coupled system of simple neural oscillators with delays, Journal of Computational and Applied Mathematics. (2009) 229, no. 1, 264–273, https://doi.org/10.1016/j.cam.2008.10.048, 2-s2.0-65049084441.
10.1016/j.cam.2008.10.048
Web of Science® Google Scholar

All articles

Z₂ × Z₃ Equivariant Bifurcation in Coupled Two Neural Network Rings

Abstract

1. Introduction

2. Elementary Analysis

3. Multiple Hopf Bifurcations

4. Computer Simulation

Conflict of Interests

References

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Z2 × Z3 Equivariant Bifurcation in Coupled Two Neural Network Rings

Abstract

1. Introduction

2. Elementary Analysis

3. Multiple Hopf Bifurcations

4. Computer Simulation

Conflict of Interests

References

Figures

References

Related

Information

Z₂ × Z₃ Equivariant Bifurcation in Coupled Two Neural Network Rings