This paper is concerned with a local method for the solution of one-dimensional parabolic equation with nonlocal boundary conditions. The method uses a coordinate transformation. After the coordinate transformation, it is then possible to obtain exact solutions for the resulting equations in terms of the local variables. These exact solutions are in terms of constants of integration that are unknown. By imposing the given boundary conditions and smoothness requirements for the solution, it is possible to furnish a set of linearly independent conditions that can be used to solve for the constants of integration. A number of examples are used to study the applicability of the method. In particular, three nonlinear problems are used to show the novelty of the method.

1. Introduction

In this paper we consider a numerical method for 1-D heat conduction problems with nonlocal boundary conditions. Such problems appear very naturally in a number of physical systems including heat conduction [1], elastic deformation of thermoelastic rods [2, 3], chemical reactions [4, 5], population dynamics [6], and petroleum exploration [7]. A recent review of problems with nonlocal boundary conditions can also be found in [8] and references therein. Traditional finite difference methods have been shown to have problems in accuracy [9]; therefore, a number of investigators have developed various numerical methods for the above problem. Recent results include methods based on θ-based finite difference [10], reproducing kernel space [11], and Adomian expansion [12].

The purpose of this paper is to apply a method based on local coordinates. We have developed this method for the solution of a Stefan problem [13]. The algorithm transforms the working equations onto a local coordinate system. It is then possible to write down an exact solution which is valid and can be used within a small local region. The procedure leads to an implicit scheme that is first order accurate in time. However, the accuracy in time can be easily improved. The novelty of the method is in the fact that it can obtain exact solutions in space based on local coordinates. In addition, the algorithm can be applied to a large class of nonlinear problems. The formulation provides a natural way to obtain a numerical solution to the problem without any iterations which is often the case using the existing methods. The present method can provide an effective way to numerically investigate the behavior of linear and nonlinear singular parabolic equations with nonlocal source terms that lead to blowup [14, 15].

Section 2 introduces the method in detail for a 1-D parabolic problem. Section 3 studies the stability of the method and the invertibility of the coefficient matrix. Section 4 uses a number of examples to investigate the applicability of the method and compares the results to exact solutions. In particular, three nonlinear problems are studied. The last two nonlinear problems are used to show the novelty of the present method.

2. A numerical Method Based on Local Coordinates

Consider a one-dimensional heat equation with nonlocal boundary conditions given by

()

where the term q(t, x) is the heat generation, f(x) is the initial condition, and the boundary conditions are of nonlocal type. Assume that the domain is divided into m equal intervals. Consider a finite difference mesh given in Figure 1.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Finite difference mesh showing the local coordinate.

For a typical node k, consider an implicit expansion of the equation at time interval (n + 1) given by

()

where the value of

is known. Now, consider a transformation to the local coordinate, η, according to

()

In terms of the local coordinate, (2) simplifies to

()

The variable q_k denotes the heat generation function q(t, x) evaluated at time (Δt(n + 1)) and location k. (In general, it is a function of space η; however, for a first-order accurate method, the value at x = (k − 1)Δx can be used. Using Taylor series expansion, it is possible to obtain a more accurate description in terms of η; that is,

, for which exact solution can be obtained.) Treating q_k as a local constant in η function allows us to write down the exact solution of u(t, η) around every node given by

()

where now c_k and d_k are constants of integration. For m intervals, there are (m + 1) nodes. Therefore, there are M = m + 1 equations similar to (5), which describe the temperature profile; that is, k = 1,2, …, M. It follows that there are 2M constants, that is, c_k, d_k (k = 1,2, …, M) that are unknown and should be computed at each time interval. It is possible to introduce 2M linearly independent conditions. These conditions are not unique. However, a linearly independent set of conditions is given by the following.

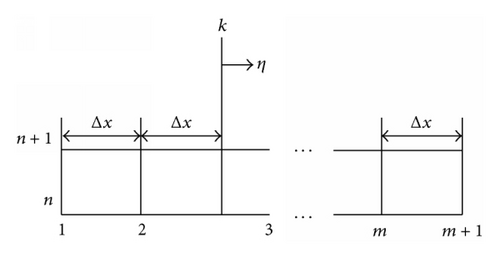
(i)
The temperature distribution at t⁽ⁿ⁺¹⁾ = (n + 1)Δt should be continuous. We can impose this condition at mid-points between nodes. It leads to
()
(ii)
The flux at t⁽ⁿ⁺¹⁾ should be continuous. In the present case, it follows that the temperature at t⁽ⁿ⁺¹⁾ should have a continuous first derivative. We can also impose this condition at mid-points between nodes. It leads to
()

The above conditions furnish (2m) linearly independent equations. The additional two conditions needed are given by the boundary conditions. The solution must satisfy the boundary conditions at x = 0 and x = 1. These conditions are nonlocal and can be imposed according to

()

The integral terms on the right hand side of the above equations can be computed in terms of the solutions given in (5) according to the following convention. For the first node, the domain of integration can be chosen to be [0, Δx/2]. For the nodes k = 2,3, …, m, the domains can be chosen to be [(k − 1)Δx − (Δx/2), (k − 1)Δx + (Δx/2)]. For the last node, the domain can be chosen as [1 − (Δx/2), 1]. In terms of the local coordinates η, for the interior nodes, the individual domains of integrations are all [−1/2, 1/2]. Similarly, the domain of integration is [0, 1/2] for the first node and [−1/2, 0] for the last node. Using these domains, the integral condition at x = 0 is given by

()

and for x = 1, it is given by

()

The functions ϕ(x) and ψ(x) are known, and the above integrals can be evaluated in closed forms. After evaluating the integrals, (10) leads to

()

Note that ξⁿ⁺¹ is known for all nodes, and the integral on the right hand side of (12) can be evaluated. Similarly, evaluating the integrals in (11) leads to

()

The above two conditions furnish the last two necessary equations that are needed before the coefficient matrix can be stably inverted. In the next section, we study the invertibility of the coefficient matrix and the stability of the proposed numerical scheme.

3. Analysis of the Method

The above conditions provide (2M) linearly independent equations that can be solved for the unknown coefficients c_k, d_k, k = 1,2, …, M, at each time increment. To prove the invertibility of the coefficient matrix we consider the case where ϕ(x) = ψ(x) = 1. Other kernels can be treated in a similar way. It is appropriate to group the above conditions in the following order. It is possible to place (6) (which is evaluated at η = 1/2, or, x = Δx/2) in the first row. Next, one can place (7) (which is evaluated at η = 1/2) in the second row. Following this pattern as well as evaluating two equations for every mid-point leads to (2m) equations that can be placed in the first (2m) rows of the matrix. The last two rows can be used to impose the boundary conditions given in (12) and (13). Following this manner, it is possible to group the above equations at every time interval tⁿ⁺¹ in the form of

()

where θ = λ/2, the unknown vector vⁿ⁺¹ contains the constants of itegrations at every time interval, and gⁿ⁺¹ is the known right hand side. In the above matrix equation, the constants on the right hand side are given by

()

and the parameters

and

are given by

()

It is now possible to denote and partition the above coefficient matrix according to

()

where the submatrices D, C, E₁, E_m, and F are (2 × 2) matrices. The partitioned matrices are Γ₁₁ ∈ R^{(M−2)×(M−2)}, Γ₂₂ ∈ R^(2×2), Γ₁₂ ∈ R^(M−2)×2, and Γ₂₂ ∈ R^(2×2) and are given by

()

The determinant of the coefficient matrix in (18) is given by

()

It is sufficient to show that the two determinants on the right hand side in the above equation are nonzero. The matrix Γ₁₁ can be inverted since it is an upper block matrix, and det⁡(D) = −2 ≠ 0. In order to show that the second determinant is nonzero, one can denote G = D⁻¹C and note that

()

It is also helpful to note that

()

Therefore, the second determinant on the right hand side of (20) is simplified to

()

where, for simplicity, ϵ = −(Δx/λ)(e^θ − e^−θ) = −(2Δx/λ)sinh⁡(θ), and

()

The above matrices are (2 × 2) matrices, and one can obtain an expression for the determinant. It is possible to simplify the above determinant which leads to

()

By letting

in the second summation, the above relation is further simplified to

()

Converting the rest of the terms to hyperbolic functions leads to

()

For a fixed Δt,

and the above determinant is equal to the difference between two positive monotonic functions of Δx with different slopes. Therefore, there are infinite values of Δx for which the determinant is not equal to zero.

Note that, for the case where the kernels in the boundary conditions, ϕ(x), ψ(x), are not constants, the matrix Γ₁₁ remains the same, that is, (det⁡(Γ₁₁) ≠ 0), and one needs to only check the Θ₂ in (20).

In order to study the stability of the method, one notes that the right hand side of (14) includes the terms g_k. Following (14), it follows that

()

The temperature fields

can be written in terms of the coefficients

. It follows that (14) can be written in terms of the coefficients at the previous time according to

()

where A is given as before, and B is given by

()

For stability, we require that all eigenvalues of the matrix A⁻¹B be inside the unit circle. Figure 2 shows the magnitude of the largest eigenvalue as a function of the order of the approximation m. As the mesh is refined, and Δx → 0, the magnitude of the largest eigenvalue increases. However, it stays within the unit circle, and the scheme is stable. The above stability test can also be applied to problems with variable kernel functions.

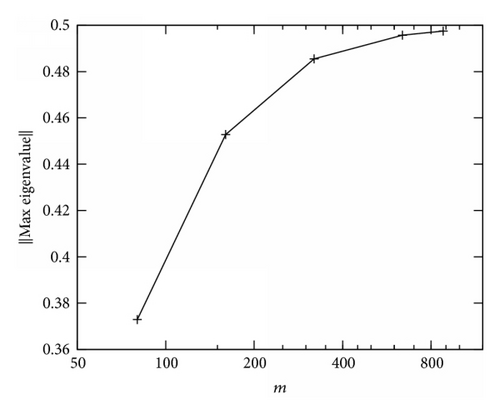
4. Numerical Examples

Example 1. Consider the heat conduction given by (1) and (2) where

()

The exact solution for the above problem is given by u(t, x) = (1 + x)(1 − e^−t − t + te^−t). Choosing the values of Δx = 0.01 and Δt = 0.00001 for the present method, Figure 3 presents the error at three locations within the domain. The method can produce numerical solution that compares well with the exact solution.

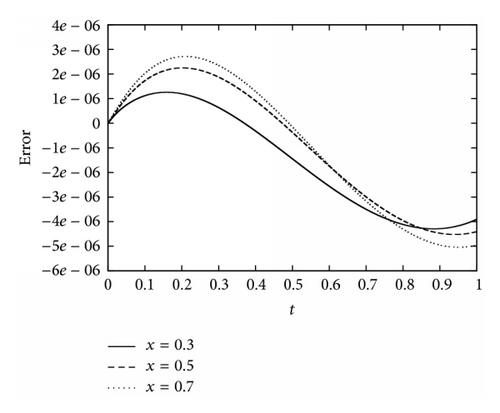
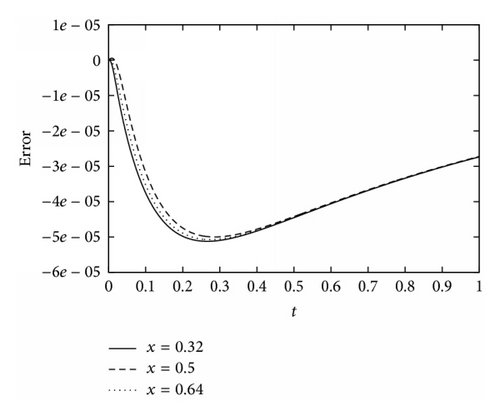
Example 2. Consider the heat conduction given by (1) and (2) where

()

This example was considered in [9, 10] to compare the standard finite difference approximations. The exact solution is given by e^−t(x(x − 1) + (δ/6(1 + δ))) for the initial condition given by f(x) = (x(x − 1) + (δ/6(1 + δ))). Using the values of δ = 0.0144, Δt = 0.0025, and Δx = 0.0025 for the present method, Figure 4 compares the computed values of temperature at x = 0.32, x = 0.5, and x = 0.64 to the exact values.

We next apply the present method to three nonlinear problems with nonlocal conditions.

Example 3. Consider the parabolic system given by

()

with

()

where E, L, and m are given constants. The above problem involves a reaction between two reactants [16]. The nonlinear term appears in the boundary condition at x = 1. Applying the present method leads to the field variable given by

()

and formulating similar continuity conditions at mid-points leads to equations similar to (6) and (7). Equation (34) can also be treated similar to (9). The nonlinear boundary condition in (33) leads to

()

where β = EmΔx/(1 + L). Note that in addition to c_k, d_k, for k = 1, …, M, the scalar θ(t) is also unknown. The nonlinear condition in (33) leads to quadratic nonlinear terms θc_M and θd_M in (36). A common approach is to set up an iteration at every time step according to

()

where

is an initial guess, which is often the value of θ at the previous time interval. It is now possible to invert the coefficient matrix and solve for the c_k, d_k, for k = 1, …, M and θ. One can use this value of θ for

and repeat this process until the values converge. This is often the usual approach when one is faced with solving a nonlinear problem. We follow this approach in this example. Using the values of E = 100, m = 1, and L = 0.01 from [16], and letting Δx = 1/50 and Δt = 0.0005, one can obtain the numerical results for the above problem. Figure 5 presents the numerical results using the present algorithm for θ(t) and u(t, 1) as a function of time. The results compare very well with the results reported in [16]. In particular, Table 1 compares the computed values of θ(t) and u(t, 1) for a few time instants. Note that the reported results in [16] are also approximate solutions and are reported after interpolation and retaining a few terms in the power series. We next consider a fully nonlinear problem and show the effectiveness of the present method. For a large class of nonlinear problems, the present method can provide a linear solution with no need for iterations at every time interval.

Table 1. Comparison of the computed values of θ(t) and u(t, 1) with the truncated results reported in [16] for E = 100, L = 0.01, and m = 1.0.

Time	Reference [16] truncated θ	Present	Reference [16] truncated u(t, 1)	Present
t = 0.4	0.6739	0.6877	0.0389	0.0419
t = 1.0	0.8613	0.8788	0.0776	0.0798
t = 2.4	0.9046	0.9047	0.0951	0.0950

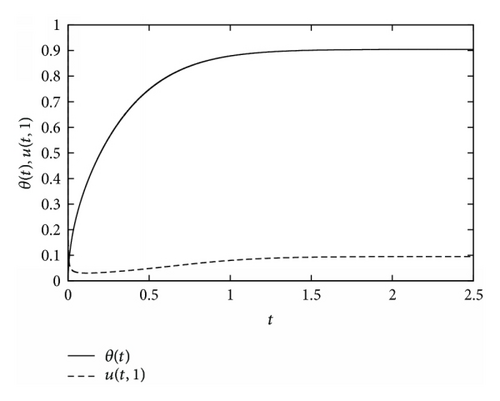
Example 4. Consider the reaction-diffusion system given by [17]

()

where a numerical method based on finite difference, which involves iterations, was presented. Applying the present method it is possible to formulate a numerical method which does not need iterations and requires the inversion of only one matrix. Using the constant values of D = 0.1, a = 5 and following the steps in (2) and (3) one can arrive at

()

Denoting λ² = Δx²(40 + (10/Δt)) and noting that ϵ = 10Δx² ≪ 1, it is now possible to look for a solution in the form of u = u₀ + ϵu₁ + ϵ²u₂ + ⋯. Considering various orders of ϵ leads to

()

Applying the same procedure to the boundary condition given in (38) leads to

()

and for various orders of ϵ

()

The above equations are linear, and applying the local formulation for various orders of approximation will require the inversion of only one matrix. The exact solution is given by

()

where

()

Dividing the domain into 400 intervals, that is, Δx = 1/400, and using Δt = 0.0005, Figure 6 presents the absolute values of the error between the computed values and the exact solution. Note that the method requires the inversion of one matrix with dimension (401 × 401) only. For this case ϵ = 0.000625 and the first two terms in the expansion of u(η) are sufficient.

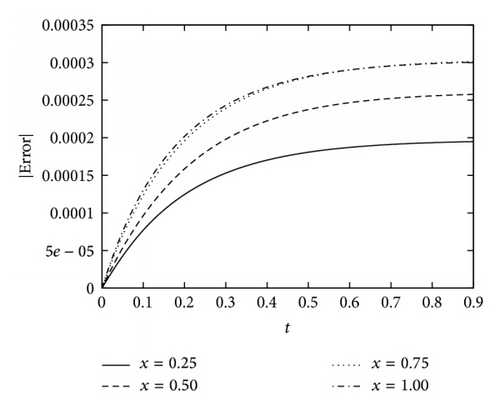
Example 5. Consider the reaction-diffusion system given by [18]

()

For this system the quantity

is conserved. The above model appears in the study of biological and chemical systems [18]. Our interest here is towards the numerical simulation of this model, and in particular the appearance of nonlinear terms. Following the approach presented here as well as writing the above equation in terms of local coordinates leads to

()

Denoting λ² = Δx²/Δt and noting that ϵ = Δx² ≪ 1, it is possible to seek a solution in the form of u = u₀ + ϵu₁ + ϵ²u₂ + ⋯, which leads to

()

Similar to the previous example, we only need to solve linear systems at each order of ϵ. In fact, they all require the inverse of the same matrix. As a result, the present method requires the inversion of only one matrix. Dividing the domain into 80 intervals, that is, Δx = 1/100, as well as using Δt = 0.000125 leads to ϵ = 0.0001. Depending on the initial condition, the above system can lead to blowup or a steady-state solution [18]. Consider the numerical solution of the above system when the initial condition is given by

()

Starting from the above initial condition, the steady state solution is a constant value of

. Figure 7 shows the difference between the conserved value

and its value at t = 0, that is,

. The method requires the inversion of only one matrix.

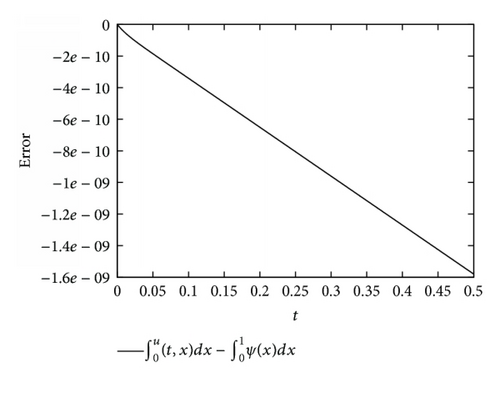
5. Conclusion

In this paper we presented a local method for obtaining the solution for 1-D parabolic problems with nonlocal boundary conditions. The method is first order accurate in time. However, the solution is locally exact in the space dimension. The order of accuracy in time can easily be improved to second order. Five numerical examples were used to study the applicability of the method. In particular, three nonlinear problems were studied to show the strength of the method.

Conflict of Interests

The authors declare that there is no conflict of interests regarding the publication of this paper.

References

1 Cannon J. R. and van der Hoek J., Diffusion subject to the specification of mass, Journal of Mathematical Analysis and Applications. (1986) 115, no. 2, 517–529, https://doi.org/10.1016/0022-247X(86)90012-0, MR836243, 2-s2.0-0022709536.
10.1016/0022-247X(86)90012-0
Google Scholar
2 Bouziani A., On the quasi static flexure of a thermoelastic rod, Communications in Applied Analysis. (2002) 6, no. 4, 549–568, MR1932320.
Google Scholar
3 Day W. A., Extensions of a property of the heat equation to linear thermoelasticity and other theories, Quarterly of Applied Mathematics. (1982) 40, no. 3, 319–330, MR678203.
Google Scholar
4 Choi Y. S. and Chan K. Y., A parabolic equation with nonlocal boundary conditions arising from electrochemistry, Nonlinear Analysis. Theory, Methods & Applications. (1992) 18, no. 4, 317–331, https://doi.org/10.1016/0362-546X(92)90148-8, MR1150422, 2-s2.0-0001265252.
10.1016/0362-546X(92)90148-8
Google Scholar
5 Capasso V. and Kunisch K., A reaction-diffusion system arising in modelling man-environment diseases, Quarterly of Applied Mathematics. (1988) 46, no. 3, 431–449, MR963580.
Google Scholar
6 Furter J. and Grinfeld M., Local vs. non-local interactions in population dynamics, Journal of Mathematical Biology. (1989) 27, no. 1, 65–80, https://doi.org/10.1007/BF00276081, MR984226, 2-s2.0-0002444698.
Google Scholar
7 Li T.-T., A class of nonlocal boundary value problems for partial differential equations and its applications in numerical analysis, 28, 49–62, 2-s2.0-0024774382, https://doi.org/10.1016/0377-0427(89)90320-8, MR1038831.
Google Scholar
8 Štikonas A., A survey on stationary problems, Green′s functions and spectrum of Sturm-Liouville problem with nonlocal boundary conditions, Nonlinear Analysis: Modelling and Control. (2014) 19, no. 3, 301–334, MR3228776.
Google Scholar
9 Ekolin G., Finite difference methods for a nonlocal boundary value problem for the heat equation, BIT: Numerical Mathematics. (1991) 31, no. 2, 245–261, https://doi.org/10.1007/BF01931285, MR1112221, 2-s2.0-0001463181.
Google Scholar
10 Liu Y., Numerical solution of the heat equation with nonlocal boundary conditions, Journal of Computational and Applied Mathematics. (1999) 110, no. 1, 115–127, ZBL0936.65096, MR1715575, https://doi.org/10.1016/S0377-0427(99)00200-9, 2-s2.0-0033569563.
Google Scholar
11 Mu L. and Du H., The solution of a parabolic differential equation with non-local boundary conditions in the reproducing kernel space, Applied Mathematics and Computation. (2008) 202, no. 2, 708–714, ZBL1149.35356, 2-s2.0-48049105310, https://doi.org/10.1016/j.amc.2008.03.008, MR2435704.
Google Scholar
12 Bougoffa L. and Rach R., Solving nonlocal initial-boundary value problems for linear and nonlinear parabolic and hyperbolic PDEs by the Adomian expansion, Applied Mathematics and Computation. (2013) 225, 50–61.
Google Scholar
13 Tadi M., A fixed-grid local method for 1-D Stefan problems, Applied Mathematics and Computation. (2012) 219, no. 4, 2331–2341, https://doi.org/10.1016/j.amc.2012.08.024, MR2983936, ZBL1291.65309, 2-s2.0-84867577056.
Google Scholar
14 Zhou J. and Mu C., Blowup for a degenerate and singular parabolic equation with non-local source and absorption, Glasgow Mathematical Journal. (2010) 52, no. 2, 209–225, https://doi.org/10.1017/S0017089509990280, MR2610968, ZBL1206.35153, 2-s2.0-77951135730.
Google Scholar
15 Chen Y., Liu Q., and Xie C., Blow-up for degenerate parabolic equations with nonlocal source, Proceedings of the American Mathematical Society. (2004) 132, no. 1, 135–145, https://doi.org/10.1090/S0002-9939-03-07090-4, MR2021256, 2-s2.0-0742306334.
Google Scholar
16 Dixon J. A., A nonlinear weakly singular Volterra integro-differential equation arising from a reaction-diffusion study in a small cell, Journal of Computational and Applied Mathematics. (1987) 18, no. 3, 289–305, ZBL0625.65143, 2-s2.0-0023363083, MR898770, https://doi.org/10.1016/0377-0427(87)90003-3.
Google Scholar
17 Pao C. V., Numerical solutions of reaction-diffusion equations with nonlocal boundary conditions, Journal of Computational and Applied Mathematics. (2001) 136, no. 1-2, 227–243, MR1855894, ZBL0993.65094, 2-s2.0-0035501484, https://doi.org/10.1016/S0377-0427(00)00614-2.
Google Scholar
18 Budd C., Dold B., and Stuart A., Blowup in a partial differential equation with conserved first integral, SIAM Journal on Applied Mathematics. (1993) 53, no. 3, 718–742, https://doi.org/10.1137/0153036, MR1218381, 2-s2.0-0027608196.
Google Scholar

Citing Literature

All articles

A Numerical Method for 1-D Parabolic Equation with Nonlocal Boundary Conditions

Abstract

1. Introduction

2. A numerical Method Based on Local Coordinates

3. Analysis of the Method

4. Numerical Examples

5. Conclusion

Conflict of Interests

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

A Numerical Method for 1-D Parabolic Equation with Nonlocal Boundary Conditions

Abstract

1. Introduction

2. A numerical Method Based on Local Coordinates

3. Analysis of the Method

4. Numerical Examples

5. Conclusion

Conflict of Interests

References

Citing Literature

Figures

References

Related

Information