The present paper analyzes a two-unit cold standby system wherein both units may become operative depending upon the demand. Initially, one of the units is operative while the other is kept as cold standby. If the operative unit fails or the demand increases to the extent that one operative unit is not capable of meeting the demand, the standby unit becomes operative instantaneously. Thus, both units may become operative simultaneously to meet the increased demand. Availability in three types of upstates is as follows: (i) when the demand is less than or equal to production manufactured by one unit; (ii) when the demand is greater than whatever produced by one unit but less than or equal to production made by two units; and (iii) when the demand is greater than the produces by two units. Other measures of the system effectiveness have also been obtained in general case as well as for a particular case. Techniques of semi-Markov processes and regenerative processes have been used to obtain various measures of the system effectiveness.

1. Introduction

In the literature of reliability, extensive studies have been made on different types of one-unit or two-unit standby redundant systems owing to their frequent use in modern business and industrial systems. There are two major types of redundancy—parallel and standby. In parallel redundancy, the redundant units form part of the system from the start, whereas in a standby system the redundant units do not form part of the system from the start (until they are needed). Standby units can be classified as cold, warm, or hot. A cold standby is completely inactive and since it is not hooked up, it cannot fail until it is replacing the primary unit. A warm standby has a diminished load because it is only partially energized. A hot standby is fully active in the system (although redundant).

A lot of work has been done on reliability and cost analysis of various systems by various researchers including [1–17] who have analyzed these systems by considering various concepts like the Erlangian repair time, operating and rest periods, hardware/software faults, congestion of calls, availability, two types of repair facility, human failure, regenerative point technique, priority repair discipline, instruction, accident, patience time, chances of nonavailability of expert repairman, one big unit and two small identical units with priority for operation/repair to big unit, patience time, partial failures, and optimized maintenance of the diesel system in locomotives. In all such studies, the demand was fixed. There may be situations where demand may vary and hence it affects the operability of the units of a system. The concept of variation in demand has been studied by [18, 19]. This concept of variation in demand was considered for single unit systems, where the system either is in working state on some demand or is put to shut down mode on no demand. However, the demand may be much more than whatever produced by a single unit system and hence there is need of having one additional unit to meet the demand. Study of the concept of variation in demand for the two-unit system thus becomes more important.

Keeping the above observations in view, we, in the present paper, develop a reliability model for a two-unit standby system working in a cable manufacturing plant wherein cold standby may become operative depending on demand. Information of such a system was gathered on visiting a cable manufacturing plant in H.P., India. It was observed that there were two units in the plant which were used to manufacture polyvinyl chloride (PVC) wires as per the demand in the market. If the demand is less than whatever produced by one unit, only one unit is kept operative, whereas if demand is greater than the production from a single unit, both units are put to operative mode. Various measures of the system effectiveness are analyzed by making use of semi-Markov processes and regenerative point techniques.

The rest of the paper is organized as follows. In Section 2, we develop the proposed semi-Markov model and presented its description. In Section 3, we find the steady-state probabilities and mean sojourn times. Section 4 deals with the computation of steady-state measures, such as mean time to system failure (MTSF), availability in three types of upstates (i.e., when demand is less than or equal to production made by one unit; when demand is greater than production made by one unit, but less than or equal to production made by two units; when demand is greater than production made by two units), busy period of the repairman for repair, and expected number of visits by the repairman. In Section 5, cost-benefit has been obtained as a general case. On the basis of the data/information estimated from the cable manufacturing plant, a particular case has been discussed in Section 6 and various graphs have been plotted in Section 7. Final conclusions along with some future directions are presented in Section 8.

2. Model Description and Assumptions

Figure 1 depicts the state transition model which we developed for a two-unit standby system working in a cable manufacturing plant wherein cold standby may become operative depending on demand. If one or both units are in working mode, then the system is in operative state. When both units are not working, that is, one is under repair and the other is waiting to be repaired, the system will stay in the failed state.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

State transition diagram.

Various assumptions for the model are as follows.

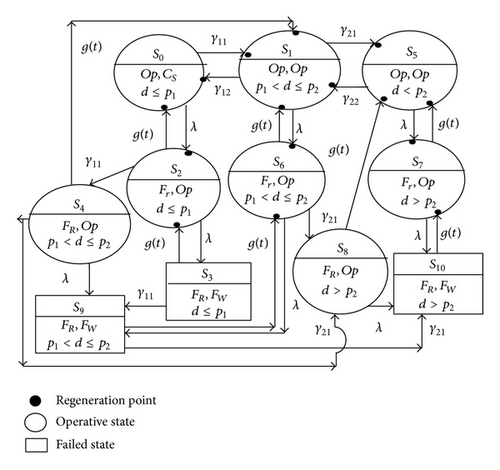
(1)
The units are similar and statistically independent.
(2)
Demand cannot be decreased further, when at the most one unit is operative.
(3)
Each unit is new after repair.
(4)
If a unit is failed, standby unit takes over automatically.
(5)
The system becomes inoperable when both units fail in a two-unit system.
(6)
All the random variables are independent.
(7)
Switching is perfect and instantaneous.
(8)
Failure and repair time follow exponential and general time distribution, respectively.

3. Transition Probabilities and Mean Sojourn Times

The transition diagram showing the various states of the system is shown as in Figure 1. The epochs of entry into states S₀, S₁, S₂, S₅, S₆, and S₇ are regeneration points and thus are regenerative states. States S₃, S₉, and S₁₀ are failed states. The transition probabilities are

()

Clearly, for the model to be accurate, it is important to estimate accurately the model parameters (i.e., mean sojourn times and the steady-state transition probabilities).

The nonzero elements

are obtained as

()

By these transition probabilities, it can be verified that

()

The mean sojourn time (μ_i) in state i is

()

Analysis carried out in this paper depends only on the mean sojourn time and is independent of the actual sojourn time distributions for the semi-Markov processes states. If we were to carry out a transient analysis of the semi-Markov processes, this will no longer be true. The unconditional mean time taken by the system to transit for any state j when it is counted from epoch of entrance into state i is mathematically stated as

()

Thus,

()

where

4. Measures of System Effectiveness

4.1. Mean Time to System Failure

To determine the mean time to system failure (MTSF) of the system, we regard the failed states as absorbing states. By probabilistic arguments, we obtain the following recursive relations for ϕ_i(t), where i = 0,1, 2,5, 6,7 are given by

()

Taking Laplace-Stieltjes Transform (L.S.T.) of the relations given by (7) and solving them for Ls(ϕ₀(t)), we obtain

()

where

()

Now, the reliability R(t) of the system at time t is given as

()

Now, the mean time to system failure (MTSF) when the system starts from the state “0” is

()

Using L’Hospital rule and putting the value of Ls(ϕ₀(t)) from (8), we have

()

where

()

4.2. Availability Analysis When Demand Is Less Than or Equal to Production Made by One Unit (d ≤ p₁)

Letting

where i = 0,1, 2,5, 6,7 as the probability that the system is in upstate when demand is not less than production made by one unit at instant t given that it entered the state i at t = 0 and using the arguments of the theory of the regeneration process, the availability

is seen to satisfy the following recursive relations:

()

where

and

()

Taking Laplace transforms of above equations (14) and solving them for A₀*(s), we get

()

where

()

In steady-state, the availability

of the system is given by

()

where

()

4.3. Availability Analysis When Demand Is Greater Than the Production Made by One Unit and Less Than or Equal to Production Made by Two Units (p₁ < d ≤ p₂)

Letting

where i = 0,1, 2,5, 6,7 as the probability that the system is in upstate when demand is greater than the production made by one unit and less than or equal to production made by two units at instant t given that it entered the state i at t = 0 and proceeding in the similar fashion as in 5.2, in steady-state, the availability

is given by

()

where

()

and D₁ is already specified.

4.4. Availability Analysis When Demand Is Greater Than Production Made by Two Units (d > p₂)

Letting

where i = 0,1, 2,5, 6,7 as the probability that the system is in upstate when demand is greater than the production made by two units at instant t given that it entered the state i at t = 0 and proceeding in the similar fashion as in Section 4.2, the availability

in steady-state is given by

()

where

()

and D₁ is already specified.

4.5. Busy Period Analysis of the Repairman

The total fraction of the time for which the system is under repair of the repairman, in steady-state, is given by

()

where

()

and D₁(s) is already specified.

4.6. Expected Number of Visits by the Repairman

The expected number of visits per unit time by the repairman, in steady-state, is given by

()

where

()

and D₁ is already specified.

5. Cost-Benefit Analysis

The expected profit can be calculated by expected total revenue in (0, t] minus expected total repair in (0, t] minus expected cost of visits by repairman in (0, t]. Hence the total profit in (0, t] is given by

()

In steady-state, the expected profit per unit time incurred to the system is given by

()

where C₀ is revenue per unit uptime when demand is less than or equal to production made by one unit (d ≤ p₁), C₁ is revenue per unit uptime when demand is greater than the production made by one unit and less than or equal to production made by two units (p₁ < d ≤ p₂), C₂ is revenue per unit uptime when demand is greater than the production made by two units (d > p₂), C₃ is cost per unit uptime for engaging the repairman for repair, and C₄ is cost per visit of the repairman.

6. Particular Case

For the particular case, let us take g(t) = αe^−αt and the values estimated from the system, that is, γ₁₁ = 0.235/hr, γ₁₂ = 0.07/hr, γ₂₁ = 0.4213/hr, γ₂₂ = 0.353/hr, α = 1/hr,λ = 0.003/hr, C₀ = INR 7000, C₁ = INR 1000, C₂ = INR 200, C₃ = INR 100, and C₄ = INR 400 (all costs are in Indian rupees).

Various measures of the system effectiveness are given by the following:

(i)
mean time to system failure (MTSF) = 100534.2109 hrs;
(ii)
steady-state availability when demand is less than or equal to production made by one unit (d ≤ p₁) ;
(iii)
steady-state availability when demand is greater than the production made by one unit and less than or equal to production made by two units (p₁ < d ≤ p₂) ;
(iv)
steady-state availability when demand is greater than the production made by two units (d > p₂) ;
(v)
busy period of the repairman for repair (B₀) = 0.004613;
(vi)
expected number of visits by the repairman (V₀) = 0.0157;
(vii)
profit incurred to the system = INR 101.3576.

7. Graphical Analysis

For the numerical results, let us take g(t) = αe^−αt, where α is repair rate. Data/information was gathered on failure and repair times from cable manufacturing system. On the basis of the gathered information, the following values are estimated:

()

Various graphs have been plotted for the MTSF, the availability, and the profit with respect to rates/revenue per unit uptime for different values of rates/costs. Some have been shown here and the others have not been shown to avoid space. The following interpretations can be made from the graphs.

(i)
MTSF gets decreased with increase in the values of failure rate but increased with increase in the values of repair rate. The values of other parameters per hour are taken as
()
(ii)
The graph of availability () when demand is less than or equal to whatever production given by a single unit (d ≤ p₁) versus failure rate (λ) for different values of repair rate (α) shows that it gets decreased monotonically with increase in the values of failure rate but increases with increase in the values of repair rate. Similar behavior has been shown for the availability () when demand is greater than the production by one unit but less than or equal to production made by two units (p₁ < d ≤ p₂) and also for the availability () when demand is greater than the production made by two units (d > p₂). The graphs revealed that the availabilities in three types of the upstates (), (), () are different in magnitude for the same values of parameters λ, α, γ₁₁, γ₁₂, γ₂₁, and γ₂₂.
(iii)
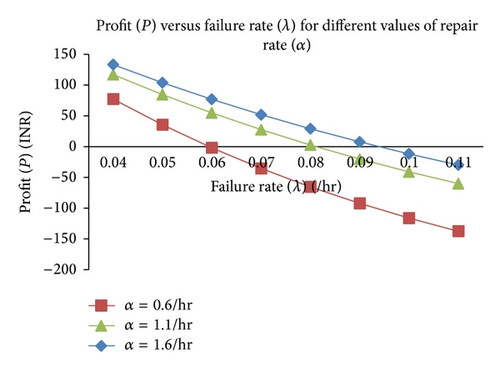
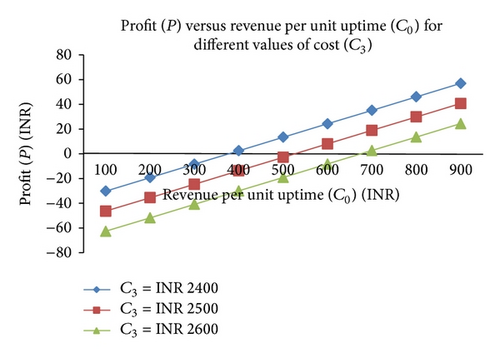
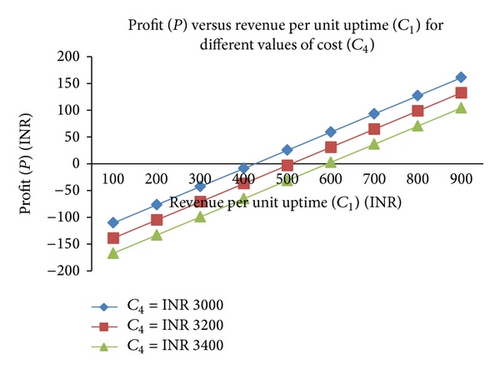
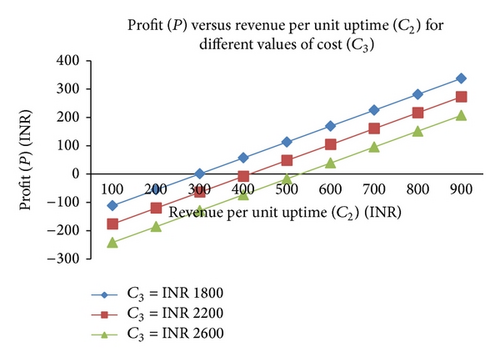
Behavior of the profit with respect to failure rate/revenue per unit uptime for different values of repair rate/cost of engaging the repairman has also been observed from the graphs. Some of these graphs are shown in Figures 2, 3, 4, and 5. The graphs depict that the profit gets decreased with increase in the values of failure rate and also with the increase in cost of engaging/visiting the repairman but increases with increase in the values of repair rate/revenue per unit uptime.

Cut-off points as to when the profit is positive or negative have been obtained from the graphs and are shown in Table 1.

Fixed parameter	Varied parameter	Profit
Fixed parameter	Varied parameter	Positive	Negative	Zero (cut-off point)
γ₁₁ = 0.235/hr, γ₁₂ = 0.07/hr, γ₂₁ = 0.4213/hr, γ₂₂ = 0.353/hr, C₀ = INR 7000, C₁ = INR 1000, C₂ = INR 200, C₃ = INR 100, C₄ = INR 400	α = 0.6/hr	λ < 0.0598	λ > 0.0598	λ = 0.0598
	α = 1.1/hr,	λ < 0.0796	λ > 0.0796	λ = 0.0796
	α = 1.6/hr	λ < 0.0943	λ > 0.0943	λ = 0.0943

γ₁₁ = 0.235/hr, γ₁₂ = 0.07/hr, γ₂₁ = 0.4213/hr, γ₂₂ = 0.353/hr, α = 1/hr, λ = 0.003/hr, C₁ = INR 1000, C₂ = INR 200, C₄ = INR 400	C₃ = INR 2400	C₀ > 395.00	C₀ < 395.00	C₀ = 395.00
	C₃ = INR 2500	C₀ > 530.00	C₀ < 580.02	C₀ = 530.00
	C₃ = INR 2600	C₀ > 690.00	C₀ < 690.00	C₀ = 690.00

γ₁₁ = 0.235/hr, γ₁₂ = 0.07/hr, γ₂₁ = 0.4213/hr, γ₂₂ = 0.353/hr, α = 1/hr, λ = 0.003/hr, C₀ = INR 7000, C₂ = INR 200, C₄ = INR 400	C₃ = INR 1800	C₁ > 224.57	C₁ < 224.57	C₁ = 224.57
	C₃ = INR 2200	C₁ > 387.34	C₁ < 387.34	C₁ = 387.34
	C₃ = INR 2600	C₁ > 597.31	C₁ < 597.31	C₁ = 597.31

γ₁₁ = 0.235/hr, γ₁₂ = 0.07/hr, γ₂₁ = 0.4213/hr, γ₂₂ = 0.353/hr, α = 1/hr, λ = 0.003/hr, C₀ = INR 7000, C₁ = INR 1000, C₄ = INR 400	C₃ = INR 1800	C₂ > 298.12	C₂ < 298.12	C₂ = 298.12
	C₃ = INR 2200	C₂ > 399.13	C₂ < 399.13	C₂ = 399.13
	C₃ = INR 2600	C₂ > 527.82	C₂ < 527.82	C₂ = 527.82

γ₁₁ = 0.235/hr, γ₁₂ = 0.07/hr, γ₂₁ = 0.4213/hr, γ₂₂ = 0.353/hr, α = 1/hr, λ = 0.003/hr, C₁ = INR 1000, C₂ = INR 200, C₃ = INR 100	C₄ = INR 3000	C₀ > 495.63	C₀ < 495.63	C₀ = 495.63
	C₄ = INR 3100	C₀ > 580.02	C₀ < 580.02	C₀ = 580.02
	C₄ = INR 3200	C₀ > 745.19	C₀ < 745.19	C₀ = 745.19

γ₁₁ = 0.235/hr, γ₁₂ = 0.07/hr, γ₂₁ = 0.4213/hr, γ₂₂ = 0.353/hr, α = 1/hr, λ = .003/hr, C₀ = INR 7000, C₂ = INR 200, C₃ = INR 100	C₄ = INR 3000	C₁ > 422.09	C₁ < 422.09	C₁ = 422.09
	C₄ = INR 3200	C₁ > 498.12	C₁ < 498.12	C₁ = 498.12
	C₄ = INR 3400	C₁ > 599.02	C₁ < 599.02	C₁ = 599.02

γ₁₁ = 0.235/hr, γ₁₂ = 0.07/hr, γ₂₁ = 0.4213/hr, γ₂₂ = 0.353/hr, α = 1/hr, λ = 0.003/hr, C₀ = INR 7000, C₁ = INR 1000, C₃ = INR 100	C₄ = INR 1800	C₂ > 298.79	C₂ < 298.79	C₂ = 298.79
	C₄ = INR 2400	C₂ > 448.07	C₂ < 448.07	C₂ = 448.07
	C₄ = INR 3000	C₂ > 599.13	C₂ < 599.13	C₂ = 599.13

8. Conclusion

A two-unit cold standby system in cable manufacturing plant wherein both units may become operative depending upon the demand has been analyzed. A state transition model that describes the dynamic behavior of such a system is used as a basis for developing a stochastic model. In this paper, we have obtained several general probability distribution functions that can be used to describe the system behavior. Various measures of system effectiveness are estimated using semi-Markov processes and regenerative point techniques. These include the following:

(i)
mean sojourn times;
(ii)
steady-state probabilities;
(iii)
mean time to system failure (MTSF);
(iv)
availability in three types of upstates (i.e., when demand is less than or equal to production made by one unit; when demand is greater than production made by one unit, but less than or equal to production made by two units; when demand is greater than production made by two units) and other measures of the system effectiveness which have been obtained in general case as well as for a particular case; it can also be concluded that these steady-state availabilities have different values in magnitude for the same value of failure rate and repair rate;
(v)
busy period of the repairman for repair;
(vi)
expected number of visits by the repairman;
(vii)
profit incurred to the system;
(viii)
various graphs which are plotted to provide a better understanding of the behaviour of the system, help to refine its stochastic description, and lead to better estimates of the model parameters;
(ix)
graphs from which the behavior of mean time to system failure, different types of availability, and the profit can be depicted with respect to failure rate/repair rate/cost for engaging repairman/revenue per unit up time/cost per visit of the repairman that have been plotted;
(x)
various cut-off points for the profit of the system which help to decide about how much should be the maximum tolerable value of the failure rate of the system and how much the cost price of the product (cable wires) manufactured by the system should be sold to get at least that value of revenue per unit uptime so as to get positive profit;
(xi)
the lower limits for the revenue per unit uptime for positive profit that have been obtained which may be quite useful for the system manufacturers, engineers, and the system analysts;
(xii)
the upper limit for the cost per visit as well as for engaging the repairman which has been obtained.

The above conclusions have been drawn on the basis of a particular case and the data collected. However, our model can be used by anyone using such system and can draw the conclusions in the similar fashion by putting those values of parameters, which exist for his/her system, in the general expressions obtained by us for the model.

Further, we are focusing on developing some more realistic models (e.g., hot standby system) related to the given system. Cost-benefit analysis for the system will be carried out to increase the uptime of the system and to reduce the cost involved in system.

Symbols for the Various States

◯:: Operative state for the system
▭:: Failed state for the system
D:: Symbol for demand
p₁:: Symbol for production by single unit
p₂:: Symbol for production by two units.

Notations

λ:: Failure rate of the operative unit
γ₁₁:: Rate of increase of demand when demand is greater than the production made by one unit and less than or equal to production made by two units (p₁ < d ≤ p₂)
γ₁₂:: Rate of decrease of demand so as to become less than or equal to production made by one unit (d ≤ p₁)
γ₂₁:: Rate of further increase of demand when demand is greater than the production made by two units (d > p₂)
γ₂₂:: Rate of decrease of demand when demand is greater than the production made by one unit and less than or equal to production made by two units (p₁ < d ≤ p₂)
:: Probability that the system is in upstate when demand is less than or equal to production made by one unit (d ≤ p₁) at instant t given that it entered the state i at t = 0
:: Probability that the system is in upstate when demand is greater than the production made by one unit and less than or equal to production made by two units (p₁ < d ≤ p₂) at instant t given that it entered the state i at t = 0
:: Probability that the system is in upstate when demand is greater than production made by two units (d > p₂) at instant t given that it entered the state i at t = 0
B_i(t):: Probability that the repairman is busy to repair the failed unit at instant t given that it entered the state i at t = 0
M_i(t):: Probability that the system, initially up in the regenerative state i, is up at time t without passing through any other regenerative state
m_ij:: Contribution to mean sojourn time in regenerative state i before transiting to regenerative state j without visiting any other state
μ_i:: Mean sojourn time in regenerative state i before transiting to any other state
′:: Symbol for derivative
*:: Symbol for Laplace transforms
Ls:: Symbol for Laplace Stieltjes transforms
⋆:: Symbol for Stieltjes convolution
q_ij(t), Q_ij(t):: p.d.f. and c.d.f of the first passage time from a regenerative state i to a regenerative state j or to a failed state j without visiting any other regenerative state in (0, t]
g(t), G(t):: p.d.f. and c.d.f of repair rate at instant t.

States of System

C_S:: Unit is in cold standby state
Op (d ≤ p₁):: Unit is in operative state when demand is less than or equal to production made by one unit
Op (p₁ < d ≤ p₂):: Unit is in operative state when demand is greater than the production made by one unit and less than or equal to production made by two units
Op (d > p₂):: Unit is in operative state when demand is greater than production made by two units
F_r:: Failed unit under repair
F_R:: Repair of failed unit continuing from previous state
F_w:: Failed unit waiting for repair.

Conflict of Interests

The authors declare that there is no conflict of interests regarding the publication of this paper.

References

1 Chandrasekhar P., Natarajan R., and Yadavalli V. S., A study on a two unit standby system with Erlangian repair time, Asia-Pacific Journal of Operational Research. (2004) 21, no. 3, 271–277, https://doi.org/10.1142/S0217595904000242, MR2098540, ZBL1056.90042, 2-s2.0-4444311437.
10.1142/S0217595904000242
Web of Science® Google Scholar
2 Goyal A., Taneja G., and Singh D. V., Reliability and profit evaluation of a 2-unit cold standby system working in a sugar mill with operating and rest periods, Caledonian Journal of Engineering. (2009) 5, 1–5.
Google Scholar
3 Kumar R. and Kapoor S., Cost-benefit analysis of a reliability model for a base transceiver system considering hardware/software faults and congestion of calls, International Journal of Science and Technology. (2012) 4, no. 6, 13–23.
CAS Google Scholar
4 Kumar R. and Kumar M., Performance and cost-benefit analysis of a hardware software system considering hardware based software interaction failures and different types of recovery, International Journal of Computer Applications. (2012) 53, no. 17, 25–32.
10.5120/8466-2387
Google Scholar
5 Madan B. B., Goševa-Popstojanova K., Vaidyanathan K., and Trivedi K. S., A method for modeling and quantifying the security attributes of intrusion tolerant systems, Performance Evaluation. (2004) 56, no. 1–4, 167–186, https://doi.org/10.1016/j.peva.2003.07.008, 2-s2.0-1042277255.
10.1016/j.peva.2003.07.008
Web of Science® Google Scholar
6 Mine H. and Kawai H., Repair priority effect on avail ability of two-unit system, IEEE Transactions on Reliability. (1979) 28, no. 4, 325–326, https://doi.org/10.1109/TR.1979.5220620, 2-s2.0-0018529906.
10.1109/TR.1979.5220620
Web of Science® Google Scholar
7 Murari K. and Goyal V., Reliability system with two types of repair facilities, Microelectronics Reliability. (1983) 23, no. 6, 1015–1025, https://doi.org/10.1016/0026-2714(83)90513-9, 2-s2.0-0020881104.
10.1016/0026-2714(83)90513-9
Web of Science® Google Scholar
8 Pandey D. and Jacob M., Cost analysis, availability and MTTF of a three state standby complex system under common cause and human failures, Microelectronics Reliability. (1995) 35, no. 1, 91–95, https://doi.org/10.1016/0026-2714(93)E0019-6, 2-s2.0-0029207390.
10.1016/0026-2714(93)E0019-6
Web of Science® Google Scholar
9 Parashar B. and Taneja G., Reliability and profit evaluation of a PLC hot standby system based on a master-slave concept and two types of repair facilities, IEEE Transactions on Reliability. (2007) 56, no. 3, 534–539, https://doi.org/10.1109/TR.2007.903151, 2-s2.0-34548612804.
10.1109/TR.2007.903151
Web of Science® Google Scholar
10 Rizwan S. M., Khurana V., and Taneja G., Reliability analysis of a hot standby industrial system, International Journal of Modelling and Simulation. (2010) 30, no. 3, 315–322, https://doi.org/10.2316/Journal.205.2010.3.205-5057, 2-s2.0-77956974751.
10.1080/02286203.2010.11442586
Google Scholar
11 Siwach B. S., Singh R. P., and Taneja G., Reliability and profit evaluation of a two-unit cold standby system with instructions and accidents, Pure and Applied Mathematika Sciences. (2001) 53, no. 1-2, 23–31, MR2157648.
Google Scholar
12 Srinivasan S. K. and Gopalan M. N., Probabilistic analysis of a two-unit system with a warm standby and a single repair facility, Operations Research. (1973) 21, 748–754, https://doi.org/10.1287/opre.21.3.748, MR0366380, ZBL0278.90026.
10.1287/opre.21.3.748
Web of Science® Google Scholar
13 Taneja G., Goyal A., and Singh D. V., Reliability and cost-benefit analysis of a system comprising one big unit and two small identical units with priority for operation/repair to big unit, Mathematical Sciences. (2011) 5, no. 3, 235–248.
CAS Google Scholar
14 Taneja G. and Naveen V., Comparative study of two reliability models with patience time and chances of non-availability of expert repairman, Pure and Applied Mathematika Sciences. (2003) 57, no. 1-2, 23–35.
Google Scholar
15 Tuteja R. K., Arora R. T., and Taneja G., Analysis of a two-unit system with partial failures and three types of repairs, Reliability Engineering & System Safety. (1991) 33, no. 2, 199–214, https://doi.org/10.1016/0951-8320(91)90059-G, 2-s2.0-0025838476.
10.1016/0951-8320(91)90059-G
Web of Science® Google Scholar
16 Trivedi K. S., Probability and Statistics with Reliability, Queuing, and Computer Science Application, 2001, 2nd edition, John Wiley & Sons, New York, NY, USA.
Google Scholar
17 Zhag Z., Gao W., Zhou Y., and Zhiqiang Z., Reliability modeling and maintenance optimization of the Diesel system in Locomotives, Maintenance and Reliability. (2012) 14, no. 4, 302–311.
Google Scholar
18 Malhotra R. and Taneja G., Reliability and availability analysis of a single unit system with varying demand, Mathematical Journal of Interdisciplinary Sciences. (2013) 2, no. 1, 77–88.
10.15415/mjis.2013.21006
Google Scholar
19 Taneja G. and Malhotra R., Cost-benefit analysis of a single unit system with scheduled maintenance and variation in demand, Journal of Mathematics and Statistics. (2013) 9, no. 3, 155–160, 2-s2.0-84878890668, https://doi.org/10.3844/jmssp.2013.155.160.
10.3844/jmssp.2013.155.160
Google Scholar

Citing Literature

All articles

Stochastic Analysis of a Two-Unit Cold Standby System Wherein Both Units May Become Operative Depending upon the Demand

Abstract

1. Introduction

2. Model Description and Assumptions

3. Transition Probabilities and Mean Sojourn Times