Volume 2014, Issue 1 850163

Research Article

Open Access

Topological Model on the Inductive Effect in Alkyl Halides Using Local Quantum Similarity and Reactivity Descriptors in the Density Functional Theory

Corresponding Author

Alejandro Morales-Bayuelo

[email protected]

Grupo de Química Cuántica y Teórica, Universidad de Cartagena, Programa de Química, Facultad de Ciencias Exactas y Naturales, Cartagena de Indias, Colombia unicartagena.edu.co

Departamento de Ciencias Químicas, Universidad Nacional Andres Bello, Republica 275, Santiago, Chile unab.cl

Search for more papers by this author

Ricardo Vivas-Reyes,

Corresponding Author

Ricardo Vivas-Reyes

[email protected]

Grupo de Química Cuántica y Teórica, Universidad de Cartagena, Programa de Química, Facultad de Ciencias Exactas y Naturales, Cartagena de Indias, Colombia unicartagena.edu.co

Search for more papers by this author

Alejandro Morales-Bayuelo,

Corresponding Author

Alejandro Morales-Bayuelo

[email protected]

Grupo de Química Cuántica y Teórica, Universidad de Cartagena, Programa de Química, Facultad de Ciencias Exactas y Naturales, Cartagena de Indias, Colombia unicartagena.edu.co

Departamento de Ciencias Químicas, Universidad Nacional Andres Bello, Republica 275, Santiago, Chile unab.cl

Search for more papers by this author

Ricardo Vivas-Reyes,

Corresponding Author

Ricardo Vivas-Reyes

[email protected]

Grupo de Química Cuántica y Teórica, Universidad de Cartagena, Programa de Química, Facultad de Ciencias Exactas y Naturales, Cartagena de Indias, Colombia unicartagena.edu.co

Search for more papers by this author

First published: 19 February 2014

https://doi.org/10.1155/2014/850163

Citations: 12

Academic Editor: Daniel Glossman-Mitnik

Share a link

Email
Wechat
Bluesky

Abstract

We present a topological analysis to the inductive effect through steric and electrostatic scales of quantitative convergence. Using the molecular similarity field based in the local guantum similarity (LQS) with the Topo-Geometrical Superposition Algorithm (TGSA) alignment method and the chemical reactivity in the density function theory (DFT) context, all calculations were carried out with Amsterdam Density Functional (ADF) code, using the gradient generalized approximation (GGA) and local exchange correlations PW91, in order to characterize the electronic effect by atomic size in the halogens group using a standard Slater-type-orbital basis set. In addition, in this study we introduced news molecular bonding relationships in the inductive effect and the nature of the polar character in the C–H bond taking into account the global and local reactivity descriptors such as chemical potential, hardness, electrophilicity, and Fukui functions, respectively. These descriptors are used to find new alternative considerations on the inductive effect, unlike to the binding energy and dipole moment performed in the traditional organic chemical.

1. Introduction

The inductive effect is one of the most important electronic effects in chemistry [1]. According to the International Union of Pure and Applied Chemistry (IUPAC) the inductive effect is defined as transmission effect of charge on a chain of atoms via electrostatic induction [2]. The inductive effect is experimentally observable via molecular polarization of polar covalent bonds produced by electrostatic induction, due to differences in electronegativity between the atoms involved [3]. In this contribution, our attention will be focused in the quantification of the molecular polarization from the point of view of the molecular bond in alkyl halides molecules such as ₃HC–X, (X = F, Cl, Br) taken as example. Using an atomic approach of molecular quantum similarity performed by Cioslowski and Nanayakkara [4] and the Molecular Quantum Similarity Indexes (MQSI) based on the electron density proposed by Carbó-Dorca and coworkers [5–9].

Several concepts and theories have been proposed in the literature in order to explain the molecular chemical bond [10–19]. Nowadays, the most used theories are the molecular orbital theory [20, 21] and the valence bond method [22, 23]. In this paper was used the concept of chemical bond as minimization of equilibrium interactions determined by the bond distances at the experimental level. We propose to relate these experimental distances with the dis(similarity) electrostatic and steric, using quantum similarity descriptors such as overlap and Coulomb indexes, with their Euclidean distances.

On the other hand, we present in this contribution a theoretical investigation in order to relate the inductive effect in these alkyl halides and analyze its dependence on the bond distance with respect to the variation of electronegativity of substituent atoms (–F, –Cl, –Br). This approach could shed some light onto some molecular aspects that can contribute to the knowledge behind interactions of these molecules.

Another reason for carrying out this study is to relate the dis(similarity) between the inductive effect and the nature of chemical bond with differences of electronegativity between atoms. In addition, this approach suggests a new perspective to the treating of the chemical bond with the inductive effect, taking into account that the search for new interpretations is a field of great interest in organic physical chemistry; in addition to the inductive effect also can be used to determine the stability of molecule with respect to their charge distribution [24–26].

2. Theory and Computational Details

2.1. Similarity Indexes

Reviews about concepts and applications in quantum similarity can be found elsewhere (see, for example, [5–9, 27, 28]); only general definitions will be given at this point. Quantum similarity provides a quantitative measure of the resemblance between two quantum objects A and B.

Carbó and coworkers introduced the similarity indexes [5, 27]; they defined the quantum similarity measure Z_AB between molecules A and B with electron density ρ_A(r₁) and ρ_B(r₂), based on the idea of minimizing the expression for the Euclidean distance:

()

where D_AB is the Euclidean distance, involving the overlap integral between the electron density Z_AB of the molecule A and B and Z_AA and Z_BB are the self-similarity of molecules A and B [27].

The most common index is the generalized quantum similarity by the cosine, introduced by Carbó et al. [28]; this index can be expressed mathematically as

()

Introducing (Z) elements in the operator (Ω) we can write

()

where (I_AB) is the Carbó index; this index is mathematically defined in the interval (0,1], where 1 is the self-similarity and calculates only the measures of “shape similarity,” as an other alternative is the of Hodgkim-Richards index [29, 30]. This index appears naturally when using the arithmetic mean and can be defined mathematically as

()

And is another alternative of quantification of the quantum similarity.

2.2. Local Similarity Indexes

2.2.1. The Hirshfeld Approach

The Hirshfeld approach [32–38]. This approach is based on partitioning the electron density ρ(r₁) of a molecule in contributions ρ_A(r₁). In this study, the Hirshfeld approach is used to express the global similarity index (4) to local level.

These contributions are proportional to the weight w_A(r₁) of the electron density of the isolated molecule in the call promolecular density [39]. The “promolecular density” is obtained as

()

The contribution of atom A ρ_A(r₁) in the electron density ρ(r₁) is

()

The weight (w_a(r₁)) is obtained as

()

where

is the electron density of the isolated atom A [40–46]. This idea has been applied in this study to CH₃–F taken as molecule A and CH₃–X, (X = Cl or Br) designating as B. The atomic contribution of carbon atom (C) in the molecule A is given by

()

with

()

For the atomic contribution of carbon atom (C) in the molecule B is obtained as

()

with

()

so that we can express the numerator in the Carbó index Z_AB in (4) as

()

where it is possible to get atomic contributions and considerations of similarity.

2.2.2. Description of Molecular Bond Proposed

To study the effects by varying electronegativity by substituents, we propose a particular characterization of the chemical bond which can be considered complementary to the Hirshfeld partition, considering that the inductive effect is dependent on the interatomic bond length [2].

We propose to study the molecular bond based on the physical concepts of bond length, defined as the minimum length (equilibrium) of the interactions according to the chemical bond model proposed by Burrau [24], these equilibrium distances are represented by (ε_eq) and we propose to multiply the equilibrium lengths (R_eq) with the (MQSI), so that we can express:

()

where I_AB is (4).

For the Euclidean distance, we have

()

where D_AB is defined in (1).

Taking into account that (ε_eq) is related with the overlap similarity index (OSI)) and with the Coulomb similarity index (CSI)) and can be interpreted as equilibrium distances that minimize the overlap and the coulomb interactions. So we can define the descriptor of chemical bonding (13) as the equilibrium distance that minimizes the structural and electronic indexes; in the sense we can express the total contributions to the molecular bond (ε_contribution (ε_c)) from the point of view of the quantum similarity indexes as

()

Equation (16) has a range of convergence of (0, 2R_eq], where 2R_eq means maximum self-similarity.

Similar to the contributions of the Euclidean distances

()

Equation (17) has a convergence range [0,∞), where 0 represents the self-similarity. This means that small distances of CH₃–F with respect to CH₃–Cl and CH₃–Br are associated with strong bonding force and a high inductive character.

3. Global and Local Reactivity Descriptors

The global reactivity descriptors are defined within the (DFT) and were interpreted by Parr and coworkers [47–54]. The chemical potential can be written mathematically in terms of the energy of an electron in the frontier molecular orbitals (higher occupied molecular orbital) HOMO and (lowest unoccupied molecular orbital) LUMO as

()

From (18), one can obtain quantitative expression for the chemical hardness (η) [48, 55–57], and it is understood as the opposition of the system to distort the electron cloud and mathematically can be written as

()

On the other hand, we have the global electrophilicity (ω) introduced by Parr et al. [58], which is a measure of the stabilization energy of the system when it is saturated by electrons from the external environment and represented mathematically as

()

The Fukui function f(r) was one of the descriptors used in this work and defined as

()

as f(r) is discontinuous at integer values of N. There are three types according to Fukui, f⁺ (22) which contains information on the reactivity local of nucleophilic attack, f⁻ (23) which does the same for an electrophilic attack [59–64]:

()

4. Molecular Alignment and Computational Details

The principal problem with the calculation of the quantum similarity measures (QSM) is the dependence the relative orientation of the molecules. The problem has been addressed through the use of several methodologies and approaches. Many critera have been used in order to deal with this problem, such as aligning the molecules according to common chemical features (e.g., three-dimensional molecular fields such as steric, electrostatic, or hydrophobic fields, among others) [65].

Also these molecules can be aligned based on topological and geometrical features as has been implemented in the Topo-Geometrical Superposition Algorithm (TGSA) [66]. In this method the alignment is based on the recognition of a common skeleton, taking only the types of atoms and bond length [67–70], in this paper the recognition of the common carbon atom was used as is shown in Figure 1.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Structures used in the molecular alignment with respect to the (CH₄), to analyze the distortion by inductive effects.

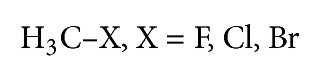
4.1. Density Functional Calculations

In order to characterize the effects by atomic size, all calculations were carried out by using the Amsterdam Density Functional (ADF) program package [71, 72]. ADF is a program for first-principle electronic structure calculations that make use of (DFT) [50]. All the molecular structures were fully optimized using the gradient generalized approximation (GGA) [73–76] local exchange correlations PW91 [77–79]. The geometry optimizations were calculated using a standard Slater-type-orbital basis set with triple-quality plus double-polarization functions for all the atoms.

5. Results and Discussion

The results reported in this work are those associated with the molecular quantum similarity indexes, followed by results of the relationship of bond proposed, and finally the results of the reactivity descriptors.

5.1. Molecular Quantum Similarity Analysis

In Tables 1–4 the (MQS) matrices for the compounds analyzed are shown, taken as an example.

Table 1. MQS matrices of overlap.

Compound	CH₃–F	CH₃–Cl	CH₃–Br
CH₃–F	1.00
CH₃–Cl	0.82	1.00
CH₃–Br	0.77	0.98	1.00

Table 2. MQS matrices of Coulomb.

Compound	CH₃–F	CH₃–Cl	CH₃–Br
CH₃–F	1.00
CH₃–Cl	0.98	1.00
CH₃–Br	0.97	0.99	1.00

Table 3. MQS matrices of Euclidean distances of overlap.

Compound	CH₃–F	CH₃–Cl	CH₃–Br
CH₃–F	0.00
CH₃–Cl	1.31	0.00
CH₃–Br	1.46	0.27	0.00

Table 4. MQS matrices of Euclidean distances of Coulomb.

Compound	CH₃–F	CH₃–Cl	CH₃–Br
CH₃–F	0.00
CH₃–Cl	2.79	0.00
CH₃–Br	3.34	0.72	0.00

In Tables 1 and 2, is possible to see that the CH₃–Cl and CH₃–Br have the higher quantum similarity with an overlap value of 0.98 and a Coulomb value of 0.99. With a Euclidean distance of Overlap of (0.27, see Table 3) and a Euclidean distance of Coulomb of 0.72 (see Table 4). The high values associated with the (MQS) of Coulomb are justified, taking into account that the alkyl halides are taken as examples of hydrocarbon derivatives in which one or more C–H bonds are replaced by C–X bonds (X = F, Cl, Br), and the similarity of C–X bond is the result of dis(similarity) in the carbon sp³ hybrid orbital; in this sense, studies based on the molecular orbital theory suggest that the hybrid orbital of the halogen is due to one small proportion p and to the s character [80]; see Figure 2.

To obtain the relations proposed in this paper the bond lengths obtained from reference [31] were used (Table 5).

Table 5. Bond length and electronegativity delta for the compounds analyzed [31].

Compound	Bond length (pm)	Δ electronegativity
	134	1.5
	176	0.5
	193	0.3

We can calculate the relations of bonding described in this study, for (MQSI) of the CH₃–Cl and CH₃–Br with respect to CH₃–F, taking into account that the strong differences in electronegativity determine the molecular polarization effects quantified by the MQSI Coulomb (Table 2).

In Table 6 the values associated with the bond relationships proposed in this study are depicted to quantify the inductive effect; with the overlap index, the values associated with the bond relationships are 109.88 pm when comparing the CH₃–F with the CH₃–Cl and 103.18 pm when compared with the CH₃–Br (see Figure 3(a)); these results are consistent with the quantum similarity indexes of overlap (see Table 1). Comparing the values associated with the relationship of bond proposed we can see that the Coulomb descriptor has the same trend (CH₃–Cl > CH₃–Br).

Table 6. Molecular binding relationships proposed in this study.

CH₃–F versus	Overlap^a (ε_O)	Coulomb^b (ε_C)	ED-overlap^c (ε_EDO)	ED-coulomb^d (ε_EDC)
CH₃–Cl	109.88	131.32	175.54	373.86
CH₃–Br	103.18	129.98	195.64	447.56

^aBonding relationship of overlap.
^bBonding relationship of coulomb.
^cEuclidean distances of overlap.
^dEuclidean distances of coulomb.

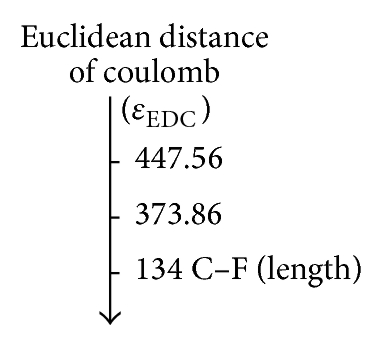
On the other hand, the predicted values for the Euclidean distance ((b) and (d)) are closest to the reference value (134 pm) of CH₃–F with respect to CH₃–Cl and CH₃–Br, respectively, reflecting the strong correlation between the molecular set from the electrostatic point of view, such that trends were sketched by the proposed scales and ae in agreement with the theoretical and experimental studies about the effect of the halogen substituent [81–83].

5.2. Analysis of Global and Local Reactivity Descriptors

Although the C–H bonds of alkyl halides are covalent and have some polar character, because the halogens are more electronegative than the carbon; in order to characterize from the chemical reactivity point of view, the polar character (C–H) is calculated in the global and local reactivity descriptions based in DFT.

In Table 7 we can see that the CH₃–Cl is the most stable compound with chemical potential of μ = −4.09 eV and the most reactive compound is the CH₃–F with μ = −3.14 eV. While the CH₃–Br have a chemical potential intermediate with a value μ = −3.81 eV, the analysis of the chemical potential leads to some general comments. The difference in chemical potential and electronegativity among the alkyl halides is also shown in the greatest opposition to the electronic flow from the electron cloud, and this conclusion is obtained with the value of chemical hardness to CH₃–F with η = 5.97 eV and η = 3.60 eV to CH₃–Br. On the other hand, such trend is also observed with the values of ionization potential of the CH₃–Br with a value of IP = 7.41 eV with the most low energy to remove electrons from the electron cloud and the electron affinity EA = 0.21 eV.

Table 7. Global reactivity indexes.

Compounds

μ^a

(eV)

η^b

(eV)

IP^c

(eV)

EA^d

(eV)

ω^e

(eV)

CH₃–F

−3.14

5.97

9.10

−2.83

0.83

CH₃–Cl

−4.09

3.97

8.06

0.12

2.10

CH₃–Br

−3.81

3.60

0.21

2.02

μ^a : chemical potential.
η^b: chemical hardness.
IP^c: Ionization potential.
EA^d: electron affinity.
ω^e: electrophilicity.

The electrophilic character is calculated with the largest stabilization energy when it is saturated by electrons from the external environment, with a value of ω: 0.83 eV to CH₃–F, ω: 2.10 eV to CH₃–Cl, and ω: 2.02 eV to CH₃–Br. Shows that these global reactivity indexes are appropriate to study the chemical reactivity of inductive effect from a different way than that has been done in the chemical literature (binding energy). Figure 4 shows the trends of the global reactivity descriptors.

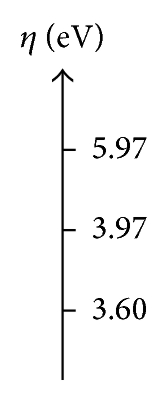
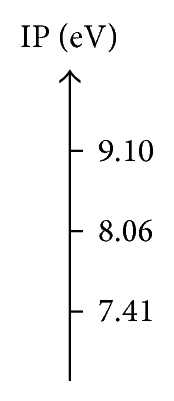
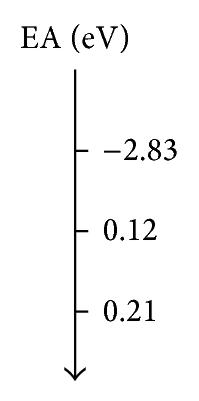
Figure 4 shows the same trend to the hardness (η) and the ionization potential (IP). According to the trends of overlap and Coulomb similarity indexes (see Figure 3), enabling the relationship of the trends in the quantum similarity descriptors of overlap and Coulomb with the chemical hardness (η) and the ionization potential (IP).

On the other hand, the trend in the electron affinity (EA) is in agreement with those found for the Euclidean distances of overlap and Coulomb and can be associated with a high electronic similarity determined by the differences in electronegativity in the molecular set and calculated by the Coulomb operator; see Table 2. In order to analyze the type of interactions present in C–X and C–H bonds the condensed Fukui functions were calculated as it shown in Table 8 to develop the topological model presented in this study.

Table 8. Local reactivity indexes.


Atoms	f⁺	f⁻	ω⁺	Atoms	f⁺	f⁻	ω⁺	Atoms	f⁺	f⁻	ω⁺

1C	0.38	0.12	0.32	1C	0.53	0.03	1.11	1C	0.45	0.02	0.91
2H	0.20	0.14	0.17	2H	0.01	0.00	0.02	2H	0.02	0.00	0.04
3H	0.20	0.04	0.17	3H	0.01	0.02	0.02	3H	0.02	0.02	0.04
4H	0.20	0.04	0.17	4H	0.01	0.02	0.02	4H	0.02	0.02	0.04
5F	0.02	0.66	0.02	5Cl	0.42	0.92	0.88	5Br	0.49	0.95	0.99

The values of the Fukui function of CH₃–F on carbon atom are f⁺: 0.38 and f⁻: 0.66 (see Table 8), respectively. Is evident that the molecular polarization due to the delta of electronegativity (Table 5) together with the value of the Fukui function (f⁻: 0.66) represents the high susceptibility of attacks by electrophilic species. These values found are in agreement with the calculated for the polar character of the hydrogen atoms due to the fluoride in the C–H bond. To observe this type of interactions in Figure 5 the topological Fukui functions f⁺: 0.38 and f⁻: 0.66 are shown for the CH₃–F, and also we can see the polar character of the C–H bonds and their contributions to the chemical reactivity due to the inductive effect.

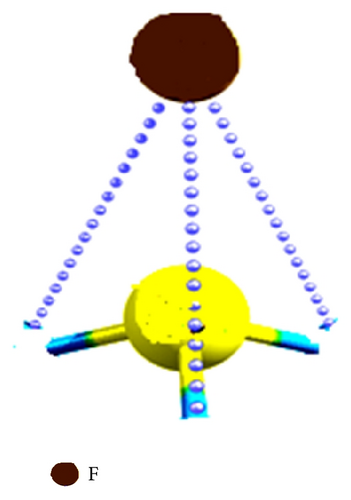
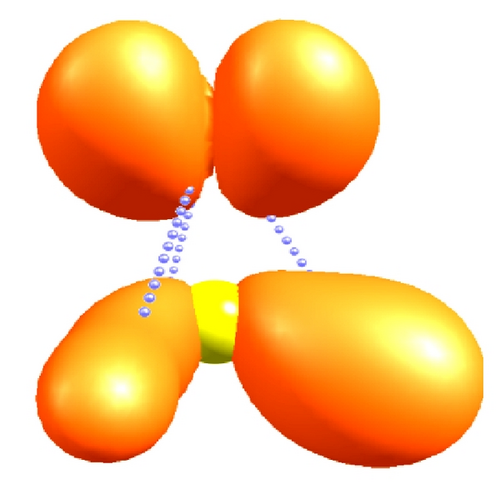
Figure 6 shows the nature of the polar interactions in the C–H bonds of CH₃–Cl through the contour maps associated with the Fukui functions f⁺: 0.53 for the carbon atom and f⁺: 0.42 for the chloride atom, and these two sites are highly reactive to nucleophilic species, unlike to the CH₃–F that only has a single reactive site f⁺: 0.38.

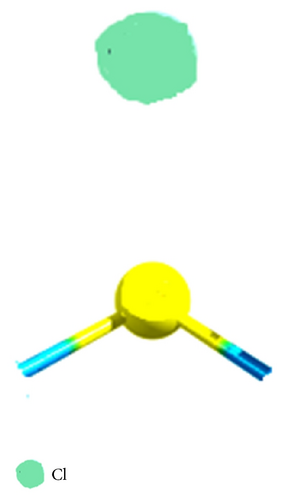
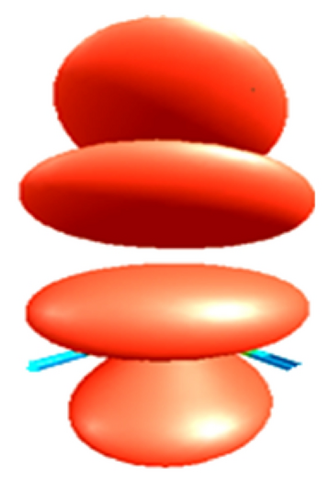
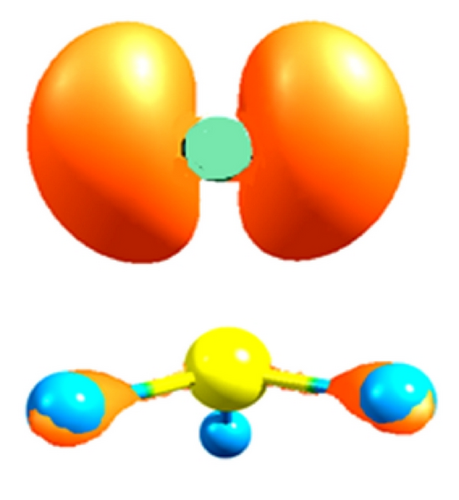
Finally, in Figure 7 the reactive sites f⁺: 0.45 for carbon and f⁺: 0.49 and f⁻: 0.95 for the bromide in the CH₃–Br are shown (see Table 8). This value for the Fukui function f⁺ shows a lower inductive effect with respect to CH₃–Cl and to the CH₃–F, respectively, according to the electronegativity values.

The inductive effect model proposed in this study provides an explanation for the polar character from a different way than that has been done in the chemical literature (through the dipole moment). On the other hand, the (ω⁺) indexes were introduced by Roy et al. [37, 84] and are expressed mathematically as

()

Equation (24) can be understood as a measure of the stabilization energy produced by the flow of electrons from the external environment for an nucleophilic attacks, and we postulate that can be related with the electrophilic character of atom more electronegative, that for the CH₃–F have (ω⁺: 0.02) in the fluoride, to the CH₃–Cl have (ω⁺: 0.88) in the chloride, and to the CH₃–Br have (ω⁺: 0.99) to the Bromide (see Table 5).

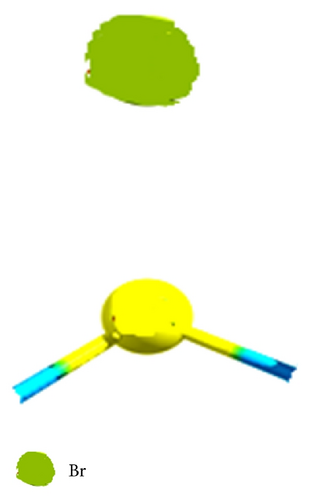
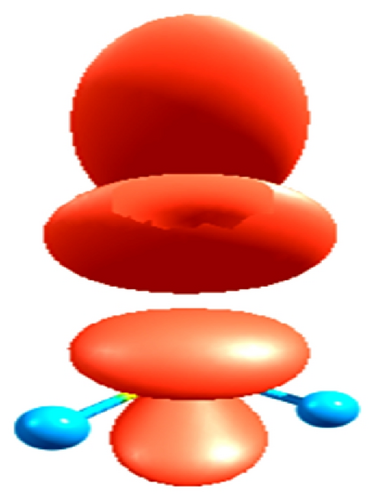
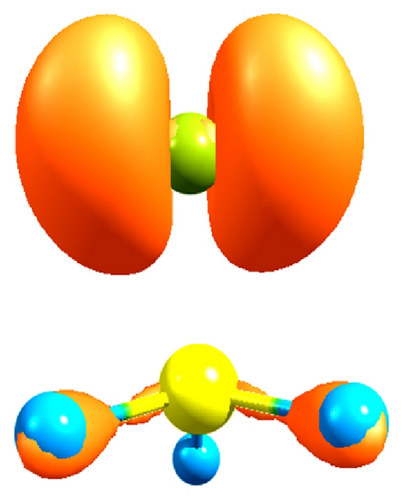
These values are quantified by the electrophilic character [81–83] produced by the inductive effect in the compounds studied, taking into account that when decrease the value of (ω⁺) increases the stabilization energy of atom most electronegative in the system when it is saturated by electrons from the external medium, and in this since, the CH₃–F has the higher inductive effect; therefore, we can see the trend (CH₃–F > CH₃–Cl > CH₃–Br) according to the trends of correlation reported in Figure 3, and these theoretical values are in agreement with experimental results [85–87].

From Figures 5–7, we can identify the polarization of covalent bonds and the prediction of reactivity sites susceptible to attack by electrophilic and nucleophilic species, allowing the analysis of the electronic density distribution in the molecular set (CH₃–F, CH₃–Cl, CH₃–Br). Taking into account that the polarization can induce a dipole in a bond near to the substituent or in one located more away (inductive effect (I)), in this sense the Fukui topological (f⁻) can interact with the electron release (+I) and the Fukui topological (f⁺) with the electron-withdrawing (−I). Although this does not imply donation formal of a unit charge, considering that by convection is assumed as electron-withdrawing groups when are most stronger than the hydrogen atom and are designated as negative inductive effects (−I).

Unlike to those groups which have a less capacity of electron withdrawing (high electron release) with respect to hydrogen atom and are designated as positive inductive effect (+I) [88], showing new considerations among the electron flow in the inductive effect and the local chemical reactivity, using the description of molecular bond proposed in this study ((13)–(17)). In this sense we analyze the quantum similarity increasing steric and electronic effects.

5.3. Quantum Dissimilarity Analysis

In order to analyze the quantum dissimilarity increasing the steric and electronic effects for analyze the stability of the relations proposed are analyzed the dissimilarity indexes in a series of isopropane derivatives shown in Figure 8.

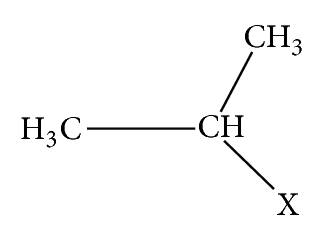
With the aim of characterizing the steric and electronic effect in Tables 9 and 10we calculate the overlap quantum dissimilarity.

Table 9. MQS matrices of overlap.

Compound	C₃H₈	C₃H₈F	C₃H₈Cl	C₃H₈Br	C₃H₈I
C₃H₈	1.0000
C₃H₈F	0.7427	1.0000
C₃H₈Cl	0.8895	0.8138	1.0000
C₃H₈Br	0.9025	0.7697	0.9887	1.0000
C₃H₈I	0.9252	0.7318	0.9536	0.9800	1.0000

Table 10. MQS matrices of Euclidean distances of overlap.

Compound	C₃H₈	C₃H₈F	C₃H₈Cl	C₃H₈Br	C₃H₈I
C₃H₈	0.0000
C₃H₈F	1.5546	0.0000
C₃H₈Cl	0.7912	1.3483	0.0000
C₃H₈Br	0.7275	1.4751	0.2608	0.0000
C₃H₈I	0.6190	1.5732	0.5214	0.3311	0.0000

In Table 9 we can see the structural effects on the atomic size, the higher overlap quantum dissimilarity values comparing C₃H₈I with C₃H₈F (0.7318), and the lowest values comparing C₃H₈Br with C₃H₈Cl (0.9887), forming the overlap quantum dissimilarity trend with respect to C₃H₈ (C₃H₈F (0.7427) > C₃H₈Cl (0.8895) > C₃H₈Br (0.9025) > C₃H₈I (0.9252)) in agreement with the trends shown in Figure 3.

In Table 10 we found the higher Euclidean distance of overlap between C₃H₈I and C₃H₈F (1.5732) and the lowest is between C₃H₈Br and C₃H₈Cl (0.2608), in agreement with the values of Table 9. With the aim of analyzing the electronic effects on the quantum dissimilarity the MQS of Coulomb are shown in Table 11.

Table 11. MQS matrices of Coulomb.

Compound	C₃H₈	C₃H₈F	C₃H₈Cl	C₃H₈Br	C₃H₈I
C₃H₈	1.0000
C₃H₈F	0.9468	1.0000
C₃H₈Cl	0.9631	0.9801	1.0000
C₃H₈Br	0.9643	0.9730	0.9990	1.0000
C₃H₈I	0.9675	0.9640	0.9947	0.9980	1.0000

In Table 11 we can see the higher electronic quantum dissimilarity value between C₃H₈F and C₃H₈ (0.9468). However, the lowest is between C₃H₈Br and C₃H₈Cl (0.9990). Also the electronic quantum dissimilarity trend with respect to C₃H₈ C₃H₈F (0.9468) > C₃H₈Cl (0.9631) > C₃H₈Br (0.9643) > C₃H₈I (0.9675) is in agreement with the outcomes of Table 9 and Figure 3. This result is consistent with the Euclidean distances of Coulomb (Table 12).

Table 12. MQS matrices of Euclidean distances of Coulomb.

Compounds	C₃H₈	C₃H₈F	C₃H₈Cl	C₃H₈Br	C₃H₈I
C₃H₈	0.0000
C₃H₈F	5.4638	0.0000
C₃H₈Cl	4.3025	2.9845	0.0000
C₃H₈Br	4.1482	3.4601	0.6427	0.0000
C₃H₈I	3.8690	3.9867	1.4585	0.8895	0.0000

In Table 12 the higher Euclidean distance of Coulomb is between C₃H₈F and C₃H₈ (5.4638), and the lowest is between C₃H₈Br and C₃H₈Cl (0.6427), in agreement with the results of Table 11. This result shows the electronegativity character and the atomic size on the steric and electronic effects related to the inductive effects and extrapolating the result of Figure 3.

6. Conclusions

We present a topological analysis on the inductive effect in CH₃–F, CH₃–Cl, and CH₃–Br alkyl halides taken as an example; using local molecular quantum similarity and chemical reactivity in DFT context, this quantification was performed through scales of quantitative convergence using descriptors based in MQSI of overlap and Coulomb (see Figure 3), presenting a good alternative relationship and the chemical bonds, and it also explains the polar character associated with the C–H bonds from the point of view of the global and local chemical reactivity, in a different way than that has been done in the chemical literature (dipole moments and energy binding); in addition these results are consistent with the effects produced by halogen substituents according to experimental results.

The alignment method used is the Topo-Geometrical Superposition Algorithm (TGSA), allowing calculating appropriate measures of the asymmetry in the central carbon atom of the alkyl halides. This TGSA method is a straightforward procedure to cope with the problem of relative orientation of the molecules to evaluate MQS; also this work shows the Hirschfield partitioning of the electronic density in the proposed model of covalent bond (see (13)–(17)) can describe and relate the inductive effect in the molecular set (CH₃–F, CH₃–Cl, and CH₃–Br).

The reactivity global indexes can characterize the reactivity of the compounds tested, the higher value of the chemical potential (μ: −3.14 eV) to the CH₃–F, with the greater hardness (η: 5.97 eV) and the most stable the CH₃–Cl with a chemical potential (μ: −4.09 eV) and (η: 3.97 eV) (see Table 7). The characterization of the reactivity sites calculated by the condensed Fukui functions (see Table 8) helped identify areas susceptible to attack by electrophilic and nucleophilic species, associating topological Fukui functions (f⁻) with the electron-release (+I) and the topological Fukui (f⁺) with the electron-withdrawing (−I).

Moreover, through this model we can be demonstrated the origin of the polar interactions of the C–H bond (see Figures 5–7) that can be applied to a much wider range of compounds such as CH₃–NH₂, CH₃–(CH₂)_n–NH₂, CH₃–OH, CH₃–(CH₂)_n–OH, CH₃–SH, and CH₃–(CH₂)_n–SH, with (n) large, due to the nature of the TGSA alignment method and in general systems where the inductive effect is marked by the high delta in electronegativity and polarizability, considering that the characterization of inductive effect is an area of growing interest in organic physical chemistry.

Conflict of Interests

The authors declare that there is no conflict of interests regarding the publication of this paper.

Acknowledgments

Alejandro Morales-Bayuelo thanks the Universidad Nacional Andres Bello (Santiago-Chile) for a Ph.D. fellowship (CONICYT (63100003)). Ricardo Vivas-Reyes is indebted to the Universidad de Cartagena (Cartagena, Colombia), for continuous support to the research group.

References

1 WadeL. G.Jr., Organic Chemistry, 2006, 6th edition, Pearson Prentice Hall, New Jersey, NJ, USA.
Google Scholar
2 Muller P., Glossary of terms used in physical organic chemistry, Pure and Applied Chemistry. (1994) 66, no. 5, 1077–1148, https://doi.org/10.1351/pac199466051077.
10.1351/pac199466051077
Web of Science® Google Scholar
3 UPAC, Compendium of Chemical Terminology, 1997, 2nd edition, Gold Book, Online corrected version (2006).
Google Scholar
4 Cioslowski J. and Nanayakkara A., Similarity of atoms in molecules, Journal of the American Chemical Society. (1993) 115, no. 24, 11213–11215, 2-s2.0-0000342623.
10.1021/ja00077a020
CAS Web of Science® Google Scholar
5 Carbó R., Arnau M., and Leyda L. J., How similar is a molecule to another? An electron density measure of similarity between two molecular structures, International Journal of Quantum Chemistry. (1980) 17, 1185–1189, https://doi.org/10.1002/qua.560170612.
10.1002/qua.560170612
CAS Web of Science® Google Scholar
6 Carbó-Dorca R. and Mercado L. D. J., Density gradient quantum similarity, Journal of Computational Chemistry. (2010) 31, 2195–2212.
10.1002/jcc.21510
CAS PubMed Web of Science® Google Scholar
7 Gironés X. and Carbó-Dorca R., Modelling toxicity using molecular quantum similarity measures, QSAR & Combinatorial Science. (2006) 25, no. 7, 579–589.
10.1002/qsar.200530128
CAS Web of Science® Google Scholar
8 Carbó-Dorca R., Besalú E., and Mercado L. D., Communications on quantum similarity. Part 3: a geometric-quantum similarity molecular superposition algorithm, Journal of Computational Chemistry. (2011) 32, no. 4, 582–599, https://doi.org/10.1002/jcc.21644.
10.1002/jcc.21644
CAS PubMed Web of Science® Google Scholar
9 Carbó-Dorca R. and Gironés X., Foundation of quantum similarity measures and their relationship to QSPR: density function structure, approximations, and application examples, International Journal of Quantum Chemistry. (2005) 101, no. 1, 8–20, https://doi.org/10.1002/qua.20191.
10.1002/qua.20191
CAS Web of Science® Google Scholar
10 Watson J. D. and Crick F., Molecular structure of nucleic acids: a structure for deoxyribose nucleic acid, Nature. (1953) 171, 737–738, https://doi.org/10.1038/171737a0.
10.1038/171737a0
CAS PubMed Web of Science® Google Scholar
11 Su P. and Li H. J., Energy decomposition analysis of covalent bonds and intermolecular interactions, The Journal of Chemical Physics. (2009) 131, no. 1, 014102, https://doi.org/10.1063/1.3159673.
10.1063/1.3159673
CAS PubMed Web of Science® Google Scholar
12 Bickelhaupt F. M. and Baerends E. J., K. B. Lipkowitz and D. B. Boyd, Reviews in computational chemistry, Wiley-VCH, 2000, 15, John Wiley and Sons, New York, NY, USA, 1–86.
Google Scholar
13 Bao P. and Yu Z., Theoretical studies on the role of π-electron delocalization in determining the conformation of N-benzylideneaniline with three types of LMO basis sets, Journal of Computational Chemistry. (2006) 27, no. 7, 809–824, https://doi.org/10.1002/jcc.20390.
10.1002/jcc.20390
CAS PubMed Web of Science® Google Scholar
14 Berry R. S., Rice S. A., and Ross J., Physical Chemistry, 1980, 1st edition, Oxford University Press, Oxford, UK.
Google Scholar
15 Berry R. S., Rice S. A., and Ross J., Physical Chemistry, 2000, 2nd edition, Oxford University Press, Oxford, UK.
Google Scholar
16 Albert Cotton F. and Wilkinson G., Advanced Inorganic Chemistry, 1962, 1st edition, John Wiley & Sons, New York, NY, USA.
Google Scholar
17 Albert Cotton F. and Wilkinson G., Advanced Inorganic Chemistry, 1999, 6th edition, John Wiley & Sons, New York, NY, USA.
Google Scholar
18 Stumm W. and Morgan J. J., Aquatic Chemistry: Chemical Equilibria and Rates in Natural Waters, 1970, 1st edition, John Wiley & Sons, New York, NY, USA.
Google Scholar
19 Stumm W. and Morgan J. J., Aquatic Chemistry: Chemical Equilibria and Rates in Natural Waters, 1996, 3rd edition, John Wiley & Sons, New York, NY, USA.
Google Scholar
20 Fleming I., Frontier Orbitals and Organic Chemical Reactions, 1977, John Wiley & Sons, New York, NY, USA.
Google Scholar
21 Houk K. N., A. P. Marchand and R. E. Lehr, Pericyclic Reactions, 1977, 2, Academic Press, New York, NY, USA, 181–271.
10.1016/B978-0-12-470502-9.50010-9
Google Scholar
22 Pauling L., The Nature of the Chemical Bond, 1960, Cornell University Press, New York, NY, USA.
Google Scholar
23 Weinhold F. and Landis C., Valency and Bonding: A Natural Bond Orbital Donor-Acceptor Perspective, 2005, Cambridge University Press, Cambridge, UK.
10.1017/CBO9780511614569
Google Scholar
24 Burrau Ø., Berechnung des energiewertes des wasserstoffmolekel-ions (H⁺₂) im normalzustand, Naturwissenschaften. (1927) 15, no. 1, 16–17, 2-s2.0-34250963347, https://doi.org/10.1007/BF01504875.
10.1007/BF01504875
CAS Web of Science® Google Scholar
25 Dumont E. and Chaquin P., Inductive effects on proton affinity of benzene derivatives: analysis using fictitious hydrogen atoms, Journal of Physical Chemistry A. (2009) 113, no. 12, 2990–2994, 2-s2.0-63849325318, https://doi.org/10.1021/jp806871r.
10.1021/jp806871r
CAS PubMed Web of Science® Google Scholar
26 Smith A. P., McKercher A. E., and Mawhinney R. C., Inductive effect: a quantum theory of atoms in molecules perspective, Journal of Physical Chemistry A. (2011) 115, no. 45, 12544–12554, 2-s2.0-80855164512, https://doi.org/10.1021/jp202757p.
10.1021/jp202757p
CAS PubMed Web of Science® Google Scholar
27 Bultinck P., Gironés X., and Carbó-Dorcaz R., Molecular quantum similarity: theory and applications, Reviews in Computational Chemistry. (2005) 21, https://doi.org/10.1002/0471720895.ch2.
10.1002/0471720895.ch2
Web of Science® Google Scholar
28 Carbó R., Arnau J., and Leyda L., How similar is a molecule to another? An electron density measure of similarity between two molecular structures, International Journal of Quantum Chemistry. (1980) 17, no. 6, 1185–1189, https://doi.org/10.1002/qua.560170612.
10.1002/qua.560170612
CAS Web of Science® Google Scholar
29 Hodgkin E. E. and Richards W. G., Molecular similarity based on electrostatic potential and electric field, International Journal of Quantum Chemistry. (1987) 14, 105–110, https://doi.org/10.1002/qua.560320814.
10.1002/qua.560320814
CAS Google Scholar
30 Hodgkin E. E. and Richards W. G., Molecular similarity, Chemische Berichte. (1988) 24.
Google Scholar
31 Weast R. C., Handbook of Chemistry & Physics, 65th edition, CRC Press, New York, NY, USA.
Google Scholar
32 Hirshfeld F. L., Bonded-atom fragments for describing molecular charge densities, Theoretica Chimica Acta. (1977) 44, no. 2, 129–138, https://doi.org/10.1007/BF00549096.
10.1007/BF00549096
CAS Web of Science® Google Scholar
33 Nalewajski R. F. and Parr R. G., Information theory, atoms in molecules, and molecular similarity, Proceedings of the National Academy of Sciences. (2000) 97, no. 12, 8879–8882, https://doi.org/10.1073/pnas.97.16.8879.
10.1073/pnas.97.16.8879
CAS PubMed Web of Science® Google Scholar
34 Parr R. G., Ayers P. W., and Nalewajski R. F., The Journal of Physical Chemistry A, 2005, 109, no. 17, 3957–3959, https://doi.org/10.1021/jp0404596.
10.1021/jp0404596
Google Scholar
35 de Proft F., van Alsenoy C., Peeters A., Langenaeker W., and Geerlings P., Atomic charges, dipole moments, and Fukui functions using the Hirshfeld partitioning of the electron density, Journal of Computational Chemistry. (2002) 23, no. 12, 1198–1209, https://doi.org/10.1002/jcc.10067.
10.1002/jcc.10067
CAS PubMed Web of Science® Google Scholar
36 Ayers P. W., Information theory, the shape function, and the hirshfeld Atom, Theoretical Chemistry Accounts. (2006) 115, no. 5, 370–378, https://doi.org/10.1007/s00214-006-0121-5.
10.1007/s00214-006-0121-5
CAS Web of Science® Google Scholar
37 Roy R. K., Pal S., and Hirao K., On non-negativity of Fukui function indices, The Journal of Chemical Physics. (1999) 110, no. 17, article 8236, https://doi.org/10.1063/1.478792.
10.1063/1.478792
Web of Science® Google Scholar
38 de Proft F., Vivas-Reyes R., Peeters A., van Alsenoy C., and Geerlings P., Hirshfeld partitioning of the electron density: atomic dipoles and their relation with functional group properties, Journal of Computational Chemistry. (2003) 24, no. 4, 463–470, https://doi.org/10.1002/jcc.10241.
10.1002/jcc.10241
CAS PubMed Web of Science® Google Scholar
39 Randić M., M. A. Johnson and G. M. Maggiora, Design of molecules with desired properties: molecular similarity approach to property optimization, Concept and Applications of Molecular Similarity, 1990, John Wiley & Sons, New York, NY, USA, 77–145.
Google Scholar
40 Carbó R., Leyda L., and Arnau M., How similar is a molecule to another? An electron density measure of similarity between two molecular structures, International Journal of Quantum Chemistry. (1980) 17, no. 6, 1185–1189, https://doi.org/10.1002/qua.560170612.
10.1002/qua.560170612
CAS Web of Science® Google Scholar
41 Carbó R. and Calabuig B., Molsimil-88: molecular similarity calculations using a CNDO-like approximation, Computer Physics Communications. (1989) 55, no. 1, 117–126, https://doi.org/10.1016/0010-4655(89)90070-2.
10.1016/0010-4655(89)90070-2
CAS Web of Science® Google Scholar
42 Carbó R. and Calabuig B., Molecular quantum similarity measures and N-dimensional representation of quantum objects. I. Theoretical foundations, International Journal of Quantum Chemistry. (1992) 42, no. 6, 1681–1693, https://doi.org/10.1002/qua.560420607.
10.1002/qua.560420607
CAS Web of Science® Google Scholar
43 Carbó R., Calabuig B., Vera L., and Besalú E., Molecular quantum similarity: theoretical framework, ordering principles, and visualization techniques, Advances in Quantum Chemistry. (1994) 25, 253–313, https://doi.org/10.1016/S0065-3276(08)60021-0.
10.1016/S0065-3276(08)60021-0
CAS Web of Science® Google Scholar
44 Sola M., Mestres J., Carbó R., and Duran M., Use of ab initio quantum molecular similarities as an interpretative tool for the study of chemical reactions, Journal of the American Chemical Society. (1994) 116, no. 13, 5909–5915, https://doi.org/10.1021/ja00092a047.
10.1021/ja00092a047
CAS Web of Science® Google Scholar
45 Boon G., van Alsenoy C., de Proft F., Bultinck P., and Geerlings P., Molecular quantum similarity of enantiomers of amino acids: a case study, Journal of Molecular Structure. (2005) 727, no. 1–3, 49–56, https://doi.org/10.1016/j.theochem.2005.02.012.
10.1016/j.theochem.2005.02.012
CAS Web of Science® Google Scholar
46 Boon G., van Alsenoy C., de Proft F., Bultinck P., and Geerlings P., Similarity and chirality: quantum chemical study of dissimilarity of enantiomers, Journal of Physical Chemistry A. (2003) 107, no. 50, 11120–11127, 2-s2.0-0346937294, https://doi.org/10.1021/jp035930u.
10.1021/jp035930u
CAS Web of Science® Google Scholar
47 Parr R. G. and Pearson R. G., Absolute hardness: companion parameter to absolute electronegativity, Journal of the American Chemical Society. (1983) 105, no. 26, 7512–7516, https://doi.org/10.1021/ja00364a005.
10.1021/ja00364a005
CAS Web of Science® Google Scholar
48 Parr R. G. and Yang W., Density Functional Theory of Atoms and Molecules, 1989, Oxford University Press, New York, NY, USA.
Google Scholar
49 Chermette H., Chemical reactivity indexes in density functional theory, Journal of Computational Chemistry. (1999) 20, no. 1, 129–154.
10.1002/(SICI)1096-987X(19990115)20:1<129::AID-JCC13>3.0.CO;2-A
CAS Web of Science® Google Scholar
50 Geerlings P., de Proft F., and Langenaeker W., Conceptual density functional theory, Chemical Reviews. (2003) 103, no. 5, 1793–1874, https://doi.org/10.1021/cr990029p.
10.1021/cr990029p
CAS PubMed Web of Science® Google Scholar
51 Liu S. B., Conceptual density functional theory and some recent developments, Acta Physico-Chimica Sinica. (2009) 25, no. 3, 590–600.
10.3866/PKU.WHXB20090332
CAS Web of Science® Google Scholar
52 Ayers P. W., Anderson J. S. M., and Bartolotti L. J., Perturbative perspectives on the chemical reaction prediction problem, International Journal of Quantum Chemistry. (2005) 101, no. 5, 520–534, https://doi.org/10.1002/qua.20307.
10.1002/qua.20307
CAS Web of Science® Google Scholar
53 Pearson R. G., Chemical Hardness, Applications from Molecules to Solids, 1997, John Wiley and Sons, Weinheim, Germany.
Google Scholar
54 Ayers P. W., The physical basis of the hard/soft acid/base principle, Faraday Discuss. (2007) 135, 161–190, https://doi.org/10.1039/b606877d.
10.1039/B606877D
CAS PubMed Web of Science® Google Scholar
55 Mineva T., Sicilia E., and Russo N., Density-functional approach to hardness evaluation and its use in the study of the maximum hardness principle, Journal of the American Chemical Society. (1998) 120, no. 35, 9053–9058, https://doi.org/10.1021/ja974149v.
10.1021/ja974149v
CAS Web of Science® Google Scholar
56 de Luca G., Sicilia E., Russo N., and Mineva T., On the hardness evaluation in solvent for neutral and charged systems, Journal of the American Chemical Society. (2002) 124, no. 7, 1494–1499, 2-s2.0-0037138655, https://doi.org/10.1021/ja0116977.
10.1021/ja0116977
CAS PubMed Web of Science® Google Scholar
57 Mineva T., Parvanov V., Petro I., Neshev N., and Russo, Fukui indices from perturbed Kohn−Sham orbitals and regional softness from mayer atomic valences, The Journal of Physical Chemistry A. (2001) 105, no. 10, 1959–1967, https://doi.org/10.1021/jp003458w.
10.1021/jp003458w
CAS Web of Science® Google Scholar
58 Parr R. G., von Szentpaly L., and Liu S., Electrophilicity index, Journal of the American Chemical Society. (1999) 121, no. 9, 1922–1924, https://doi.org/10.1021/ja983494x.
10.1021/ja983494x
CAS Web of Science® Google Scholar
59 Parr R. G. and Yang W., Density functional approach to the frontier-electron theory of chemical reactivity, Journal of the American Chemical Society. (1984) 106, no. 14, 4049–4050, https://doi.org/10.1021/ja00326a036.
10.1021/ja00326a036
CAS Web of Science® Google Scholar
60 Perdew J. P., Parr R. G., Levy M., and BalduzJ. L.Jr., Density-functional theory for fractional particle number: derivative discontinuities of the energy, Physical Review Letters. (1982) 49, 1691–1694, https://doi.org/10.1103/PhysRevLett.49.1691.
10.1103/PhysRevLett.49.1691
CAS Web of Science® Google Scholar
61 Yang W. T., Zhang Y. K., and Ayers P. W., Degenerate ground states and a fractional number of electrons in density and reduced density matrix functional theory, Physical Review Letters. (2000) 84, 5172–5175, https://doi.org/10.1103/PhysRevLett.84.5172.
10.1103/PhysRevLett.84.5172
CAS PubMed Web of Science® Google Scholar
62 Yang W. T., Parr R. G., and Pucci R., The Journal of Chemical Physics, 1984, 81, no. 6, article 2862, https://doi.org/10.1063/1.447964.
10.1063/1.447964
Google Scholar
63 Ayers P. W., Yang W. T., and Bartolotti L. J., P. K. Chattaraj, Fukui function, Chemical Reactivity Theory: A Density Functional View, 2009, CRC Press, Boca Raton, Fla, USA, 255–267.
10.1201/9781420065442.ch18
Google Scholar
64 Ayers P. W. and Levy M., Perspective on ‘density functional approach to the frontier-electron theory of chemical reactivity’, Theoretical Chemistry Accounts. (2000) 103, no. 3-4, 353–360, https://doi.org/10.1007/s002149900093.
10.1007/s002149900093
CAS Web of Science® Google Scholar
65 Morales-Bayuelo A., Ayazo H., and Vivas-Reyes R., Three-dimensional quantitative structure-activity relationship CoMSIA/CoMFA and LeapFrog studies on novel series of bicyclo [4.1.0] heptanes derivatives as melanin-concentrating hormone receptor R1 antagonists, European Journal of Medicinal Chemistry. (2010) 45, no. 10, 4509–4522, 2-s2.0-77956184489, https://doi.org/10.1016/j.ejmech.2010.07.011.
10.1016/j.ejmech.2010.07.011
CAS PubMed Web of Science® Google Scholar
66 Gironés X., Robert D., and Carbó-Dorca R., TGSA: a molecular superposition program based on topo-geometrical considerations, Journal of Computational Chemistry. (2001) 22, no. 2, 255–263.
10.1002/1096-987X(20010130)22:2<255::AID-JCC12>3.0.CO;2-2
CAS Web of Science® Google Scholar
67 Morales-Bayuelo A., Torres J., and Vivas-Reyes R., Hückel treatment of pyrrole and pentalene as a function of cyclopentadienyl using local quantum similarity index (LQSI) and the topo-geometrical superposition approach (TGSA), Journal of Theoretical and Computational Chemistry. (2012) 11, no. 1, 223–239, 2-s2.0-84857200749, https://doi.org/10.1142/S0219633612500150.
10.1142/S0219633612500150
CAS Web of Science® Google Scholar
68 Morales-Bayuelo A., Baldiris R., Torres J., Torres J. E., and Vivas-Reyes R., Theoretical study of the chemical reactivity and molecular quantum similarity in a series of derivatives of 2-adamantyl-thiazolidine-4-one using density functional theory and the topo-geometrical superposition approach, International Journal of Quantum Chemistry. (2012) 112, no. 14, 2681–2687, https://doi.org/10.1002/qua.23288.
10.1002/qua.23288
CAS Web of Science® Google Scholar
69 Morales-Bayuelo A., Torres J., and Vivas-Reyes R., Quantum molecular similarity analysis and quantitative definition of catecholamines with respect to biogenic monoamines associated: scale alpha and beta of quantitative convergence, International Journal of Quantum Chemistry. (2012) 112, no. 14, 2637–2642, https://doi.org/10.1002/qua.23284.
10.1002/qua.23284
CAS Web of Science® Google Scholar
70 Morales-Bayuelo A. and Vivas-Reyes R., Topological model to quantify the global reactivity indexes as local in Diels—Alder reactions, using density function theory (DFT) and local quantum similarity (LQS), Journal of Mathematical Chemistry. (2013) 51, no. 1, 125–143, https://doi.org/10.1007/s10910-012-0069-8.
10.1007/s10910-012-0069-8
CAS Web of Science® Google Scholar
71 Amsterdam Density Functional (ADF) Code, Vrije Universiteit: Amsterdam, The Netherlands, 2007.
Google Scholar
72 Young D., Computational Chemistry, 2001, John Wiley & Sons, New York, NY, USA.
10.1002/0471220655
Google Scholar
73 Langreth D. C. and Perdew J. P., Theory of nonuniform electronic systems. I. Analysis of the gradient approximation and a generalization that works, Physical Review B. (1980) 21, no. 12, 5469–5493, 2-s2.0-3843060308, https://doi.org/10.1103/PhysRevB.21.5469.
10.1103/PhysRevB.21.5469
Web of Science® Google Scholar
74 Langreth D. C. and Perdew J. P., Theory of nonuniform electronic systems. I. Analysis of the gradient approximation and a generalization that works, Physical Review B. (1980) 21, no. 12, 5469–5493, 2-s2.0-3843060308, https://doi.org/10.1103/PhysRevB.21.5469.
10.1103/PhysRevB.21.5469
Web of Science® Google Scholar
75 Perdew J. P. and Wang Y., Accurate and simple density functional for the electronic exchange energy: generalized gradient approximation, Physical Review B. (1986) 33, no. 12, 8800–8802, https://doi.org/10.1103/PhysRevB.33.8800.
10.1103/PhysRevB.33.8800
CAS PubMed Web of Science® Google Scholar
76 Perdew J. P., Density-functional approximation for the correlation energy of the inhomogeneous electron gas, Physical Review B. (1986) 33, no. 12, 8822–8824, https://doi.org/10.1103/PhysRevB.33.8822.
10.1103/PhysRevB.33.8822
CAS PubMed Web of Science® Google Scholar
77 Perdew J. P. and Wang Y., Accurate and simple analytic representation of the electron-gas correlation energy, Physical Review B. (1992) 45, no. 23, 13244–13249, https://doi.org/10.1103/PhysRevB.45.13244.
10.1103/PhysRevB.45.13244
CAS PubMed Web of Science® Google Scholar
78 Perdew J. P., Burke K., and Ernzerhof M., Generalized gradient approximation made simple, Physical Review Letters. (1996) 77, no. 18, 3865–3868, https://doi.org/10.1103/PhysRevLett.77.3865.
10.1103/PhysRevLett.77.3865
CAS PubMed Web of Science® Google Scholar
79 Perdew J. P., Chevary J. A., Vosko S. H., Jackson K. A., Pederson M. R., Singh D. J., and Fiolhais C., Atoms, molecules, solids, and surfaces: applications of the generalized gradient approximation for exchange and correlation, Physical Review B. (1992) 46, no. 11, 6671–6687, 2-s2.0-23244460838, https://doi.org/10.1103/PhysRevB.46.6671.
10.1103/PhysRevB.46.6671
CAS PubMed Web of Science® Google Scholar
80 Katritzky A. R. and Topsom R. D., The σ- and π-inductive effects, Journal of Chemical Education. (1971) 48, no. 7, 427–431, 2-s2.0-0008019387.
10.1021/ed048p427
CAS Web of Science® Google Scholar
81 Liu S. B., P. K. Chattaraj, Chemical Reactivity Theory: A Density Functional View, 2009, Taylor and Francis, Boca Raton, Fla, USA.
Google Scholar
82 Chattaraj P. K., Sarkar U., and Roy D. R., Electrophilicity index, Chemical Reviews. (2006) 106, no. 6, 2065–2091, 2-s2.0-33745756260, https://doi.org/10.1021/cr040109f.
10.1021/cr040109f
CAS PubMed Web of Science® Google Scholar
83 Chattaraj P. K., Maiti B., and Sarkar U., Philicity: a unified treatment of chemical reactivity and selectivity, Journal of Physical Chemistry A. (2003) 107, no. 25, 4973–4975, 2-s2.0-0037742281, https://doi.org/10.1021/jp034707u.
10.1021/jp034707u
CAS Web of Science® Google Scholar
84 Roy R. K., Krishnamurti S., Geerlings P., and Pal S., Local softness and hardness based reactivity descriptors for predicting intra- and intermolecular reactivity sequences: carbonyl compounds, The Journal of Physical Chemistry A. (1998) 102, no. 21, 3746–3755, https://doi.org/10.1021/jp973450v.
10.1021/jp973450v
CAS Web of Science® Google Scholar
85 Moncada J. L. and Morán G. S., Caracterización de la reactividad intrínseca de los halobencenos en el modelo conceptual de la teoría de funcionales de la densidad (TFD), Anales de Química. (2007) 103, no. 3, 23–27.
Google Scholar
86 McMurry J., Organic Chemistry, 1996, 4th edition, Brooks/Cole Publishing, Albany, NY, USA.
Google Scholar
87 Neils S. I., Physical Organic Chemistry, 1995, 2nd edition, Longman Scientific and Technical Singapore Publishers, Singapore.
Google Scholar
88 Tchoubar B., Mecanismos de Reacción en Química Orgánica, 1965, Limusa, México City, Mexico.
Google Scholar

Citing Literature

All articles

Topological Model on the Inductive Effect in Alkyl Halides Using Local Quantum Similarity and Reactivity Descriptors in the Density Functional Theory

Abstract

1. Introduction

2. Theory and Computational Details

2.1. Similarity Indexes

2.2. Local Similarity Indexes

2.2.1. The Hirshfeld Approach

2.2.2. Description of Molecular Bond Proposed

3. Global and Local Reactivity Descriptors

4. Molecular Alignment and Computational Details

4.1. Density Functional Calculations

5. Results and Discussion

5.1. Molecular Quantum Similarity Analysis

5.2. Analysis of Global and Local Reactivity Descriptors

5.3. Quantum Dissimilarity Analysis

6. Conclusions

Conflict of Interests

Acknowledgments

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Topological Model on the Inductive Effect in Alkyl Halides Using Local Quantum Similarity and Reactivity Descriptors in the Density Functional Theory

Abstract

1. Introduction

2. Theory and Computational Details

2.1. Similarity Indexes

2.2. Local Similarity Indexes

2.2.1. The Hirshfeld Approach

2.2.2. Description of Molecular Bond Proposed

3. Global and Local Reactivity Descriptors

4. Molecular Alignment and Computational Details

4.1. Density Functional Calculations

5. Results and Discussion

5.1. Molecular Quantum Similarity Analysis

5.2. Analysis of Global and Local Reactivity Descriptors

5.3. Quantum Dissimilarity Analysis

6. Conclusions

Conflict of Interests

Acknowledgments

References

Citing Literature

Figures

References

Related

Information