A Multistep Extending Truncation Method towards Model Construction of Infinite-State Markov Chains
Abstract
The model checking of Infinite-State Continuous Time Markov Chains will inevitably encounter the state explosion problem when constructing the CTMCs model; our method is to get a truncated model of the infinite one; to get a sufficient truncated model to meet the model checking of Continuous Stochastic Logic based system properties, we propose a multistep extending advanced truncation method towards model construction of CTMCs and implement it in the INFAMY model checker; the experiment results show that our method is effective.
1. Introduction
Continuous Time Markov Chains (CTMCs) have been used in various areas of research as a formalism; so far, the model checking of CTMCs has been a hot research topic in computer science research communities. Some algorithms and implementations have been shown in several papers and tools [1–7]. However, our research aims to the model checking problem of the Infinite-State CTMCs, which means that the states of the CTMCs in our interest can be infinite. The papers [8–11] and the tool INFAMY [7] are with the same interest, which are also our research basis. Due to the explosion of states of CTMCs, our approach is based on a truncated CTMC model, which is determined by the exploration on the fly [9, 10], which means that the depth of model is computed dynamically by the exploration of states.
The truncation process is involved with reachability analysis [9, 10]; that is, the transient probability is computed with the exploration of the model. The transient probability is carried out by uniformization method [10]. Together with the transient analysis when constructing the model, computation is very heavy, so to get a sufficient truncated model to meet the requirement of related Continuous Stochastic Logic (CSL) property or certain precision as fast as possible is our destination. We introduce a multistep extending advanced truncation method to meet this end, and the experimental results show our method is effective.
The main contents of the paper are organized as follows. Section 2 introduces the truncation based reachability analysis; Section 3 introduces an advanced truncation algorithm and do experiments. Section 4 proposes some multistep extending solutions and experiments. Section 5 talks about our result and next job.
2. Truncation Based Reachability Analysis
2.1. Finite Truncations
Let 𝒞 = (S, R, L) be a CTMC, where S is a countable set of states, R : (S × S → ℝ≥0) is the rate matrix, and L : S → 2AP is a labeling function.
First, we introduce some paths and probabilistic measures from [9]. A (timed) infinite path is an infinite sequence σ = s1t1s2t2… satisfying R(si, si+1) > 0, and ti ∈ ℝ≥0 for all i = 1,2, …. For the path σ and i ∈ N, let σ[i] = si denote the (i + 1)th state, and let δ(σ, i) = ti denote the time spent in si. For ti ∈ ℝ≥0, let σ@t denote σ[i] such that i is the smallest index with . For 𝒞, let denote the set of all paths, and let denote the set of all paths starting from s. For state s ∈ S, a probability measure, denoted by , on the set can be defined. A finite path is a finite sequence σ = s1t1s2t2 … sk for k > 0 satisfying R(si, si+1) > 0 and ti ∈ ℝ≥0 for i = 1,2, …, k − 1. Let len(σ) = k − 1 denote the length of the path, first(σ) = s1 denote the first state, and last(σ) = sk denote the last state of the path. Let denote the set of all finite paths. We omit the superscript 𝒞 if it is clear from context.
Next, we introduce the notion of depth. Let S0 be a finite subset of S with depth 0; that is, d(s) = 0 for s ∈ S0. For now, one may think of S0 as being equal to the support of the initial distribution μ. However, S0 can be an arbitrary finite set. This will allow us not only to deal with the initial distribution, but also to compute truncation depths for nested CSL formulas. The depth of state s corresponds to the minimal distance from the set S0.
Definition 1. For 𝒞 and S0 ⊂ S, the depth function d : S → ℕ is defined by .
Observe that for all s ∈ S0. The subscript is omitted if S0 is clear from the context. Intuitively, d(s) corresponds to the minimal length of any finite path starting from S0 and ending in s.
We consider a partition of the state space S = ⋃i∈ℕ Si, where Si : = {s ∈ S∣d(s) = i} is the set of states with depth i. We say that the set Si is the layer with depth i and call its elements layer-i states. Assume that ⊥∈S is a special state not in S and furthermore ⊥ is also an atomic proposition not in AP. For k ∈ ℕ, let S>k ⊂ S denote the set of states with depth greater than k; that is, S>k = {s∣d(s) > k}.
Further, we write S≤k = S∖S>k. We define the k-truncated CTMC as follows.
Definition 2. Let 𝒞 = (S, R, L) be a CTMC and let S0 be the layer-zero states. For k ∈ ℕ, we define the k-truncated CTMC of 𝒞 by 𝒞∣k = (S∣k, Rk, Lk), where the states are S∣k = S≤k ∪ {⊥}. The labeling function Lk : S∣k → AP ∪ {⊥} is defined by Lk(s) = L(s) if s ∈ S≤k, and Lk(⊥) = {⊥}. The rate matrix is defined by the following: Rk(s, s′) equals S(s, s′) if s, s′ ∈ S≤k, equals if s ∈ Sk, s′ = ⊥, and equals 0 otherwise.
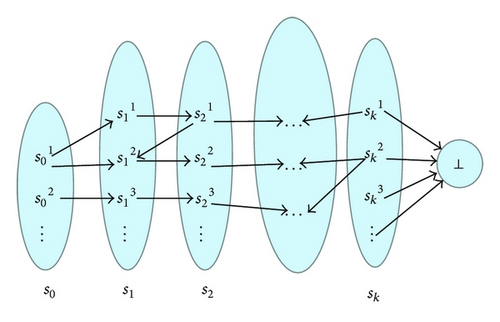
The k-truncation of an infinite CTMC is illustrated in Figure 1. Intuitively, the transition matrix is restricted to the truncated state space S∣k, and ⊥ is the distinguished absorbing state, which, by construction, is only reachable from states with depth k. In state ⊥ only the atomic proposition ⊥ holds, which indicates that the system is in state ⊥. Since we consider finitely branching CTMCs, not surprisingly, the k-truncated CTMC 𝒞∣k is always finite. The absorbing state ⊥ has been introduced to abstract S>k. We assume that ⊥∉Sat(Φ) for any state formula Φ. We consider the probability of reaching the absorbing state ⊥ in the k-truncated CTMC 𝒞∣k, that is, . For mere notational convenience, we extend to states of 𝒞 with depth higher than for all s′ ∈ S with d(s′) > k. For a fixed k, we define the forward rate frk(s) of a state s ∈ S≤k within 𝒞∣k. For s ∈ S≤k∖Sk, it is the sum of the rates that go into the next layer frk(s) = R(s, Sd(s)+1), and, for s ∈ Sk, it is the sum frk(s) = R(s, S>k) of the rates entering states in Sk.
2.2. The Logic CSL
The semantics of the state formulas and path formula are precisely defined in [10]. In this paper, the state formula like the kind of 𝒫⊴p(ϕ) will be more focused on; it means that starting some state, the probability of the system that satisfies a path formula ϕ would meet the rational relation ⊴p or not, so the first solution to this problem is to compute this probability, so this is reduced to transient analysis, which is our main interest, to improve the efficiency of transient analysis for the whole model while extending the border states layer by layer.
2.3. Transient Analysis
Transient analysis means that, starting at state s, the transient probability vector at time t, it can be denoted as . If t = 0, we have if s = s′ and 0 otherwise. The uniformization method based solution of was given at [10]. Let t > 0 and , where q is the uniformization rate satisfying q ≥ sups∈SR(s, S) and φ(i, qt) = e−qt((qt) i/i!) denotes the ith Poisson probability with parameter qt and vector is transient probability of the uniformized DTMC uni(𝒞) at step i.
The truncated model in our method is given by dynamically exploring from the initial state(s); once we want to add a layer on it, we need to compute the reachability probability from the initial(s) to the current layer states which we want to add. As shown in Figure 1, s0 is the initial states set, and each of s1, s2, …, sk is explored dynamically, so we get a k-depth truncated model of the infinite one. ⊥ is the absorbing state, which is the border states set, for which the sum of the reachability probabilities from the initial state(s) is less than ɛ; ɛ is the precision of the result, which can be 10−6, 10−9, or 10−12, and so forth, which can be set under INFAMY model checker as a circumstance variable for some certain need.
The reachability probability is carried out by the uniformization method to the CTMC, which is a relatively fast method to get the transient probability at a certain bound time t at some state, which is denoted as 𝒫(◊[0,t]s). However, if the state explosion situation is very serious, the time to construct the model layer by layer would be of much cost. So we introduce an advanced truncation algorithm to explore the states, this method can improve the efficiency of the model constructing and model checking, and then at Section 4, we further propose some multistep extending solutions, which are implemented based on INFAMY model checker, the experiment results show that these solutions can help to improve the efficiency.
3. An Advanced Truncation Algorithm and Experiments
The truncation process is implemented by extending the states layer by layer from the initial states, and all the new states need to be transient analyzed and then to be extended further no matter how small the probability is. For that the precision of the result is under some certain value, so some states with relatively nearly no contribution to the result can be omitted when extending; thus, an advanced truncation algorithm is introduced. It is different from the finite state projection (FSP) [9, 10] and layered chain and uniform chain method [9, 10]. The algorithm is shown in Algorithm 1.
-
Algorithm 1: An advanced truncation algorithm towards construction of CTMC.
-
(1) procedure TRANSIENTTRUNCADVANCED(𝒞, S0, t, ε)
-
(2) I = S0
-
(3) B = S0
-
(4) compute 𝒫I(◊[0,t]B)
-
(5) while max (𝒫I(◊[0,t]B)) ≥ ε do
-
(6) s′ = s∣𝒫s(◊[0,t]B) = max (𝒫I(◊[0,t]B))
-
(7) compute
-
(8) while do
-
(9) such that
-
(10) and
-
-
(11) B = {successors(s)∣s ∈ E}
-
(12) compute
-
(13) end while
-
(14) compute 𝒫I(◊[0,t]B)
-
(15) end while
-
(16) end procedure
The algorithm aims to stop the extending of less important (small probability) states and proceed to the extending of much important (large probability) states; the less or more is determined by the state reduction policy; as shown in Figure 2, line 7, and . The policy means that the states in the border states set, which has been sorted upward, , will be excluded from the extending states set, for the sum of them is just exactly less than the precision. So with this policy, the number of states to be transient analyzed will be smaller to the FSP and forward-layered based model.
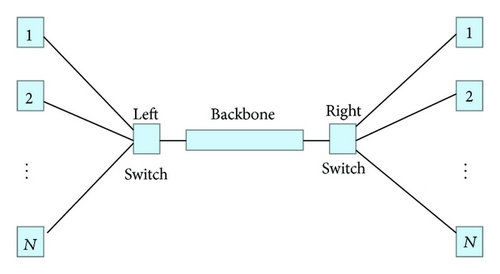
We consider the dependability of a fault-tolerant workstation cluster which is directly taken from case studies of [7]. Figure 2 depicts a dependable cluster of workstations. The cluster consists of two subclusters, which, in turn, contain N workstations connected via a central switch. The two switches are connected via a backbone. Each component of the system can break down and is then fixed by a single repair unit responsible for the entire system. Hereby, the quality of service (QoS) constraint minimum requires at least k (k < N) workstations to be operational, where k = ⌊(3/4)N⌋. Workstations have to be connected via switches. If in each subcluster the number of operational workstations is smaller than k, the backbone is required to be operational to provide the required service. We consider the property.
𝒫 = ?◊[0, t]¬Minimum. This probability means that the QoS drops below minimum quality within t time unit.
For the property, we compare PRISM [6], FSP method and layered method of INFAMY. The results are given in Tables 1, 2, and 3. Because the resulting probabilities are very small in some cases, we use a precision of 10−6 here, for the computation of the truncation point. Results for INFAMY are given for the layered chain, FSP, and advanced configurations, respectively. The uniform chain configuration is omitted, as it is always dominated by the layered chain configuration. PRISM implements three different engines: a sparse-matrix and two symbolic engines. We used the sparse-matrix engine as it was the fastest one. The results are shown in Tables 1, 2, and 3.
| Time bound t | Forward-layered | |||
|---|---|---|---|---|
| Depth | Time (s) | n | Prob | |
| 5.0 | 316 | 450 | 1668363 | [0.9E − 06, 1.50E − 06] |
| 10.0 | 517 | 661.5 | 2373652 | [3.2E − 06, 3.8E − 06] |
| 20.0 | 517 | 1293 | 2373652 | [8.8E − 06, 9.4E − 06] |
| 30.0 | 517 | 1453 | 2373652 | [1.45E − 05, 1.51E − 05] |
| 50.0 | 517 | 2096 | 2373652 | [2.61E − 05, 2.67E − 05] |
| Time bound t | Advanced | |||
|---|---|---|---|---|
| Depth | Time (s) | n | Prob | |
| 5.0 | 18 | 6.6 | 4071 | [0.9E − 06, 1.50E − 06] |
| 10.0 | 25 | 23.3 | 7118 | [3.2E − 06, 3.9E − 06] |
| 20.0 | 38 | 105.2 | 14434 | [8.8E − 06, 9.5E − 06] |
| 30.0 | 50 | 271.6 | 22426 | [1.45E − 05, 1.52E − 05] |
| 50.0 | 69 | 1491.5 | 38448 | [2.61E − 05, 2.68E − 05] |
| Time bound t | PRISM (sparse engine) | FSP | ||||
|---|---|---|---|---|---|---|
Time (s) (construct/M.C.ing) |
Prob | Depth | Time (s) | n | Prob | |
| 5.0 | 1.868/46.5 | 1.16E − 06 | 16 | 5.7 | 4405 | [0.9E − 06, 1.70E − 06] |
| 10.0 | 1.8/77.265 | 3.51E − 06 | 22 | 20.7 | 8425 | [3.2E − 06, 4.0E − 06] |
| 20.0 | 1.8/127.072 | 9.06E − 06 | 33 | 113.9 | 19161 | [8.8E − 06, 9.7E − 06] |
| 30.0 | 1.8/179.675 | 1.48E − 05 | 42 | 353.6 | 31185 | [1.45E − 05, 1.56E − 05] |
| 50.0 | 1.8/274.593 | 2.64E − 05 | 57 | 1219.7 | 57705 | [2.61E − 05, 2.73E − 05] |
The experiment conditions are shown as follows.
Host Machine: it includes Mac Book, OS: Mac OS X 10.6.8, Processor: 2.2 GHz Intel Core 2 Duo T7500, and Storage: 2 GB 667 MHz DDR3 SDRAM.
Guest Machine: it includes Virtual Machine Software: VirtualBox 4.1.14 r77440 for mac; Virtual OS: Linux ubuntu12.04 LTS 32Bit; Processor: 2.2 GHz Intel Core 2 Duo T7500; Storage: 512 MB
From Tables 1, 2, and 3, we can see that, for t ≤ 20, FSP based INFAMY is faster, but for t ≤ 30, t ≤ 50, INFAMY model checker needs more time; this is because the transient analysis when constructing the model needs more computing. This is also the result of [11]. For the advanced method of the context, as in Tables 1, 2, and 3, comparing advanced with FSP, we can get that, under advanced based method, the depth of model is much deeper, and the states number is smaller; for the time costing, for t ≤ 20, t ≤ 30, the costing is less reduced, but for t ≤ 50, the costing is greater; this result is reasonable, for the exploration policy is essentially undeterministically efficient for different models; for the current case, when t ≤ 50, the current states number is very large, even with the reduction policy, with no contribution for it any more. We need to take other techniques to tackle this situation. Thus, we propose a multistep extending solution. See Section 4.
4. Multistep Extending Solutions and Experiments
The mutistep extending solution aims to reduce the extending of less important (small probability) states and enhance the extending of more important (large probability) states; for the latter states, we can, for example, extend two or more steps per extending, and for the former states, we can, for example, extend one step per extending, as we know that transient probabilities will be computed once again before the states were added to the border states, so, if we extend two or more steps, transient analysis at the intermediate states will be omitted; thus, time on the model construction will be reduced; then we can make the model much faster to converge to the absorbing state.
- (1)
two-step extending solution, that is, B = {successors(successors(s))∣s ∈ E};
- (2)
three-step extending solution, that is, B = {successors(successors(successors(s)))∣s ∈ E};
- (3)
synthesis solution 1: a synthesis extending solution separates set E to three parts, as set E is a sorted set, which is sorted upward by the probabilities, so we can separate E as E1, E2, and E3, and the sizes of each part are the same. Then we can get
- (i)
B1 = {successors(s)∣s ∈ E1};
- (ii)
B2 = {successors(successors(s))∣s ∈ E2};
- (iii)
B3 = {successors(successors(successors(s)))∣s ∈ E3};
- (iv)
B = B1 ∪ B2 ∪ B3;
- (i)
- (4)
synthesis solution 2 separates set E to two parts, so we can separate E to E1 and E2, and the sizes of the two parts are the same. Then we can get
- (i)
B1 = {successors(s)∣s ∈ E1};
- (ii)
B2 = {successors(successors(s))∣s ∈ E2};
- (iii)
B = B1 ∪ B2.
- (i)
- (i)
E1 = {e0, e1, …, ei∣ei ≤ Prob(e0 + ProbGap/2) and ei+1 > Prob(e0 + ProbGap/2)};
- (ii)
E2 = E∖E1.
-
And then we can get that
- (i)
B1 = {successors(s)∣s ∈ E1};
- (ii)
B2 = {successors(successors(s))∣s ∈ E2};
- (iii)
B = B1 ∪ B2.
| Time bound t | Advanced (one step per extending) | Two-step per extending | Three-step per extending | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Depth | Time (s) | n | Depth | Time (s) | n | Depth | Time (s) | n | |
| 5.0 | 18 | 6.6 | 4071 | 20 | 8.9 | 4756 | 33 | 15.0 | 7895 |
| 10.0 | 25 | 23.3 | 7118 | 29 | 26.5 | 8027 | 38 | 41.3 | 11849 |
| 20.0 | 38 | 105.2 | 14434 | 42 | 115.3 | 16315 | 52 | 174.0 | 20816 |
| 30.0 | 50 | 271.6 | 22426 | 54 | 327.6 | 25308 | 64 | 456.0 | 30785 |
| 50.0 | 69 | 1491.5 | 38448 | 72 | 1006.5 | 43824 | 82 | 1572.6 | 50942 |
| t | Synthesis solution 1 | Synthesis solution 2 | Solution D | ||||||
| 5.0 | 35 | 11.9 | 6539 | 20 | 9.6 | 4564 | 20 | 8.6 | 4459 |
| 10.0 | 42 | 35.4 | 9772 | 26 | 29.7 | 7646 | 26 | 24.9 | 7383 |
| 20.0 | 53 | 131.2 | 17777 | 41 | 111.7 | 15621 | 39 | 91.1 | 15170 |
| 30.0 | 61 | 367.4 | 26362 | 53 | 279.7 | 24239 | 50 | 250.9 | 23063 |
| 50.0 | 74 | 1349.6 | 45170 | 71 | 989.1 | 42703 | 71 | 791 | 40403 |
The experiment results are as shown in Table 4. From Table 4, we can see that current solution D performs better on this case.
5. Conclusion
The multistep extending advanced truncation method can improve the efficiency of model construction of Infinite-State CTMCs; this is because the transient probabilities of states which have been jumped have not been computed, so to some extent this method is effective; however, which solution performs better needs to be experimented; there is no general solution that fits well for all cases. The efficiency is determined by the iterations when computing the transient probability. Less iteration is more efficient. However, this approach is essentially a linear approach to improve the efficiency; when the outsider state gets explosion, this approach will be less effective; just as in our case study, this approach can be used effectively to improve the model checking efficiency at a relatively small time bound t. For future work, we need to consider other techniques to tackle the state explosion problem on model checking of CTMCs. And other works like [12–15] can also be considered.
Conflict of Interests
The authors declare that there is no conflict of interests regarding the publication of this paper.
Acknowledgments
The authors would like to thank Lijun Zhang and Ernst Moritz Hahn for their original work on INFAMY model checker and the free contribution of the tool codes; Definitions 1 and 2 are directly taken from [10]. This paper is partially funded by the Communication University of China, 2013 Planned Research Program, and Research Funding Foundation of School of Computer Science, and the scholarship from China Scholarship Council for the Excellent University Teachers Study Abroad Program and supported by the National Natural Science Foundation of China (61103199), Beijing Municipal Natural Science Foundation (4112052); Supported by Engineering Program Project of CUC (3132013XNG1326, 3132013XNG1321), and the National Key Science and Technology Pillar Programs of China (2012BAH51F02, 2012BAH38F05, and 2013BAH66F02).




