The phonon contribution to the phenomenon of high temperature superconductivity in the cuprates is argued as being masked as polarons generated by the polarization of the charge reservoir accompanying the Jahn-Teller tilting of the apical oxygen. We discuss the Mahan oscillator-spring extension model as an analogy to the charge reservoir-CuO plane c-axis polarons. Using the Boltzmann kinetic equation, we show that the polaron dissociates or collapses at a temperature corresponding to the critical temperature of the superconductor.

1. Introduction

Almost three decades since the discovery of high temperature superconductivity in the cuprate La-Ba-CuO by Bednorz and Muller [1] and subsequently in many CuO based compounds by other researchers, there is still no closure about the mechanism of superconductivity in these systems [2, 3]. One of the major points of disagreement is whether phonons contribute along with the accepted spin magnetic fluctuation to the high critical temperature of the cuprates. Many researchers are in support of the phonon mechanism as the only factor responsible for the cuprates high critical temperatures [4–6].

Other workers [7–9] have considered the spin magnetic fluctuation the only adoptable theory for the cuprates. A good reason for the persistence of the “phonon-camp,” is perhaps the enduring success of the electron-phonon interaction (EPI) explanation of the low temperature superconductivity (LTS) by Bardeen, Cooper, and Schrieffer (BCS), [10]. Still another reason may be the recent discovery of superconductivity in MgB₃ at T_c = 40 K [11]; this being explained surprisingly by the EPI mechanism. It has even become very comfortable to make prognosis of still higher T_c’s in materials whose electronic properties are well understood based on the EPI. As an example we mention the EPI mechanism used by Gao and his coworkers to predict that the compound Li₂B₃C superconducts at about 50 K through the process of lifting the σ-bonding up above the Fermi level by doping, enabling σ-electrons to interact strongly with the lattice vibrations in such a way that electron pairing occurs [12]. In the LTS such as lead, tin, and aluminium, phonon contribution is indicated by the isotope effect which relates the critical temperature (T_c) to the mass (M) of the isotope atom as T_c ∝ M^−α, where α is the electron-phonon coupling constant defined as α = −dln⁡T_c/dln⁡M. The BCS value for α is 1/2 [13] which corresponds to the weak coupling regime where the Coulomb interaction is neglected. When the Coulomb interaction is taken into account, α can be approximated by δT_c/T_c = −α(δM/M), where α = (1/2)[1 − (μ^*/(λ − μ^*))] and λ is the BCS interaction parameter. Thus when the isotope shifts δT_c and T_c are known, μ^* the pseudopotential can be defined [14]. The isotope effect also plays a significant role in the cuprates: La_2−xSr_xCuO₄, YBa₂Cu₃O_7−δ, and Nd_2−xCe_xCuO₄, where x is the concentration of strontium and cerium, while δ is the oxygen vacancy. Tunneling measurements on these cuprates support a phonon mediated mechanism of superconductivity [15, 16]. Another angle to the phonon contribution to high temperature superconductivity (HTS) is in terms of polarons. A Landau-Pekar-Frohlich polaron is an electronic perturbation of an ionic crystal such that the polarized lattice interacts and moves with the electron as one entity. The first study of the motion of an electron in an ionic crystal was made by Landau [17]. A series of contributions by many researchers have followed since Landau’s work; significantly, by Pekar, Frohlich, and Feynman (for Pekar’s work, see for example, [18–20]). In recent times the EPI mechanism has been reintroduced into condensed matter physics and applied especially to high temperature superconductivity and colossal magnetoresistance by the use of polarons, with some success [5]. A substantive number of papers have addressed the important questions of polaron mass, its radius, ground state energy, and motion [21–24].

In the present work we shall study polarons in the cuprates in a somewhat different context. The theory we shall propose here consists of the following. Cooper pairs are preformed even in the pseudogap phase; Jahn-Teller tilting of the apical oxygen in the charge reservoir is responsible for the titration of the CuO plane with electrons or holes. The electrons or holes pairings are created by spin fluctuation scenario [7, 9, 25, 26]. Furthermore, every electron or hole that arrives on the CuO plane is polaronic; the Jahn-Teller tilt causes the polarization whose electrical field is responsible for creating phonons that are exchanged between the polarized ions and the electrons on the CuO plane. The exchange of phonons between the polarized ions and CuO paired electrons constitutes polarons of large radii. Two of such polarons connect the CuO plane of, for example, La_2−xSr_xCuO₄, one from above and another from below. Being massive, the polarons trap and localize the Cooper pair, releasing the pair only at the superconducting transition temperature (T_c).

2. Deformation Potential and Lattice Polarization

Consider the position X_j of a jth atom in an ionic crystal. During lattice vibration the atom is displaced as X_j = Q_j + u_j, where Q_j is the equilibrium lattice position and u_j is the displacement. Let the motion of X_j be harmonic and described by the Hamiltonian:

(1)

where p_j is the linear momentum, m is the mass, and ω_l is the longitudinal elastic eigen frequency of the atom. In (1) we can substitute the values

and

to obtain

. We may define the following operators

and

which are substituted in H₀ to give the quantum harmonic oscillator Hamiltonian:

. From the foregoing results it is easy to show that

(2)

In (2), ρ is the density of the medium, v is the volume, and b_j and

are known as the phonon annihilation and creation operators. Since u_j = u_j(r), its Fourier transform is

(3)

Let us define the deformation potential as [18]

(4)

where D_I is the deformation constant, and we find

(5)

Thus, the deformation potential becomes

(6)

The electron can interact with this potential, resulting in the electron-phonon Hamiltonian:

(7)

Here, we chose the limit of integration to reflect a positive direction of electron motion; and are the electron annihilation and creation operators, respectively.

The polarization of the lattice is defined as

(8)

where

is the unit vector of polarization and F is the polarization strength which can be determined by writing the polarization in terms of the electric field strength

and normalized atomic deviation

(9)

See [18]. In (9) ϵ₀, ϵ_∞ are the static and high frequency dielectric constants, respectively, and ω_LO is the longitudinal optical frequency. The electric field strength is given by

is the cut-off longitudinal frequency of the elastic wave related to the transverse frequency ω_t by the Lyddane-Sachs-Teller formula

. When ω_t = ω_LO and

, (9) after a little algebra becomes

(10)

where N is the number of unit cells in unit volume of crystal, μ is the reduced mass of the two ions in the unit cell, and

are the relative displacements of the positive and negative ions, 1/ϵ^* = 1/ϵ_∞ − 1/ϵ₀ and

. In the continuum approximation

(11)

Equation (10) then takes the form

(12)

Equating (8) to (12) we see that

. Let us now consider the scalar potential ϕ(r) due to the polarization by using the Poisson equation

; the solution is

(13)

Then the electron-phonon interaction can also be obtained by using (13) as follows:

(14)

Comparing (14) and (7), we obtain a value of the deformation constant D_I as .

3. The c-Axis Polaron

The formation of the c-axis polaron can be described as a spring which is anchored in the deformation potential and stretched to the CuO plane to couple with an electron of the Cooper pair as discussed in Section 1. The polaron then oscillates between these two end points allowing us to study the motion of a harmonic oscillator comprising of longitudinal phonons. The spring motion analogy of the polaron was first used by Feynman [20] and later by Mahan [27] in their works. Within the deformation potential, the ionic system becomes polarized. The polarization wave sets up an electric field

on which electrons scatter; here q denotes the wave vector. Thus

(15)

The scalar potential ϕ(r) of the electric field has already been found as (13), and an equivalent expression is obtained by noting that

, so that we can write

(16)

The potential energy of an electron in this field is thus given as

(17)

Now consider the electron-phonon Hamiltonian (14) which we rewrite in the form

(18)

where

(19)

and the matrix element of the electron-phonon transition is M² = 2πe²ℏω_l/ϵ^*. Now following [27], we write the total Hamiltonian of an electron interacting with the harmonic oscillator as

(20)

The equation of motion technique can be used to find the eigenvalue of ℋ. Indeed for the operator b_q,

(21)

A new operator system can be extracted from (21) as

. These operators satisfy the commutation relations

. Then the Hamiltonian (21) becomes

(22)

with the corresponding eigenvalue being the spring-oscillator system’s energy:

(23)

The second term of (23) is the relaxation or potential energy of the stretched spring-oscillator, which is justified as follows. Equation (3) can be written as

(24)

yielding

(25)

In the Feynman polaron theory, the unit of radius is

; therefore (25) represents the stretching of the spring-oscillator or polaron by several units. For the sake of completeness of our presentation we shall transform the second term of (23) to show that it is actually the Coulomb potential energy, as

(26)

where we have put F_q = eϕ, and volume equal to unity.

Physical processes that occur in solids at high temperatures involve large number of phonons. Since the phonon number is never conserved, then it is its average number 〈N〉 that is relevant. That means

. One method of carrying out the calculation has been given by Kittel [28], who did the averaging with respect to the first order electron wave function of perturbation theory

. Thus

, passing from summation to integration, and after some algebra one obtains the average phonon number in terms of the polaron coupling constant α as |k, 0〉

(27)

(28)

In the case of weak coupling, the self-energy of the polaron can be found by the second order perturbation theory [28]; this calculation will yield as a by-product the polaron effective mass

in terms of the electron effective mass m^* as

(29)

Since the polaron potential energy which is the second term of (23) is V(r) = −(e²/ϵ^*r) and the kinetic energy corresponding to the first term is ℏω(N + (1/2)) = π²ℏ²/2mr², then the total energy is ℰ = (π²ℏ²/2mr²)−(e²/ϵ^*r); minimizing ℰ with respect to r, the explicit form of the polaron radius and minimum energy are seen to be, respectively, [18, 29]:

(30)

4. Polaron Model of Hi-T_c Superconductivity

In this section we shall discuss our polaron model of superconductivity. We shall begin with the diagram of the model as given below in Figure 1.

Details are in the caption following the image — **Figure 1 (a)**
Open in figure viewer PowerPoint

Polaronic model: (a) CR refers to the charge reservoir, e⁺ is the positive ion obtained after polarization, e⁻ is one electron of a Cooper pair, points 1 and 1′ and 2 and 2′ are the same points of the sample but are separated by a temperature difference ΔT = T − T_c > 0, ph stands for phonons, and e^* denotes the neutral unpolarized atom. (b) The deformation potential showing the nonequilibrium distribution f at temperature T and the equilibrium distribution f₀ at temperature T_c after relaxation in time τ. The arrow shows the direction of the relaxation. If the charge on the CuO plane is a hole, then the corresponding CR charge is e⁻.

Let us assume that the charges on the CuO plane are the electrons; then the electron-phonon interaction is brought about by the exchange of phonons between the levels 1 and 1′ or states k and k^′. We denote the probability that phonons make transitions from states k to k^′ in unit time by W(k, k^′) and the probability of transitions in the reversed direction by W(k^′, k). The Boltzmann transport equation (BTE) can now be introduced in the form

(31)

Here,

is the Fermi-Dirac function, v is the velocity of the electron, r is the position vector, m is the mass, and F is the force on the electron. In the stationary state

(32)

That is, (∂f/∂t)_col = −(∂f/∂t)_field, where the field term is (∂f/∂t)_field = −v∇_rf − (1/m)F∇_vf and the collision term is

(33)

where the last equality is due to the principle of detailed balance. In nondegenerate systems, the function f becomes the Boltzmann function,

, thus making the BTE applicable to both electrons and phonons. Let us write (33) in a form conforming to point 1 of Figure 1:

(34)

The points 1 and 2 of Figure 1 are related by

(35)

and from Figure 1(b) we may form the proportionality relationship f/f₀ = T₀/T, so that f(ω) = f₀(T₀/T₁), where T_c < T₀ < T, and T₁ has been chosen slightly less than T. Then (34) becomes

(36)

and if T₀≅T₁, then we can interpret (36) as that uninterrupted phonon transition takes place between the states k and k^′, moderated by the equilibrium distribution function f₀. Now using (35) and (36) we can write for the point 2 of Figure 1, the expression

(37)

Thus, the collision integral at point 2 is written in terms of the extinction factor 1 − T/T_c which indicates the polaron’s collapse at point 2, where T = T_c. At T > T_c, the polaron energy is greater than the Cooper pair energy 2Δ. The polaron’s collapse or dissociation is associated with a polaron energy ℰ_pol = 0 and thus related to the relaxation of the deformation potential in the sense that generally

(38)

That is, when = f₀(ϵ), the collision integral’s value is given by (37) and point 2 in Figure 1. The value of the matrix elements of the transition probability W(k, k^′) has already been found to be

(39)

The last expression may directly be obtained by using the Fermi golden rule:

(40)

Equation (36) can now be written in the form

(41)

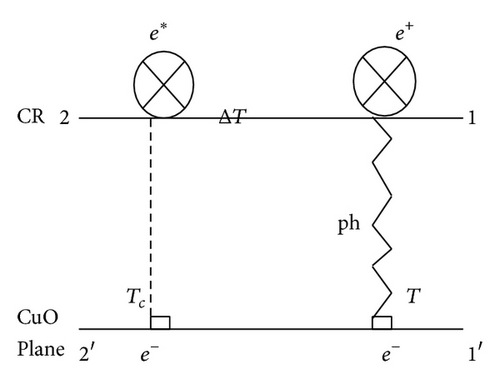
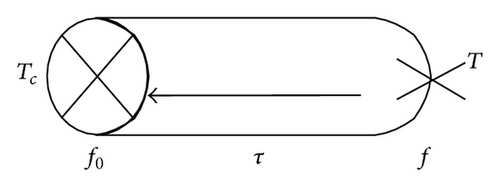
The comment made with respect to (36) also holds here.

5. Conclusion

For the stability of the polaron system, its energy ℰ_pol must be greater than the preformed Cooper pair energy 2Δ in the temperature regime T > T_c. We have assumed that the polarons are localized but oscillating along the c-axis of the cuprate, and when it collapses at T = T_c, the Cooper pair which had also been localized becomes free to make translational motion on the CuO plane. This means that for all polaronic superconductors, ℰ_pol(T = T_c) = 0. It is this symbiotic relationship between the polaron and Cooper pair that reveals the mechanism of high temperature superconductivity. Furthermore, based on (37), room temperature superconductivity (see, [30]) can be achieved (at least theoretically) by creating a high temperature polaronic cuprate and searching for T_c in it. The higher the polaron temperature is, the higher the likelihood of finding a room temperature T_c.

List of Symbols and Abbreviations

BCS:: Bardeen, Cooper, and Schrieffer
BTE:: Boltzmann transport equation
LTS:: Low temperature superconductors
ω_l:: Longitudinal elastic eigenfrequency
:: Phonon annihilation and creation operators at site j
u_j:: Atomic displacement
ρ:: Density of the medium
D_I:: Deformation constant
𝒰:: Deformation potential
:: Lattice polarization vector
:: Unit vector of polarization
F:: Polarization strength
ω_LO:: Longitudinal optical frequency
α:: Polaron coupling constant
:: Polaron effective mass
m^*:: Electron effective mass
ℰ_pol:: Polaron energy
f(ε):: Fermi-Dirac distribution function
T_c:: Critical temperature
f_o:: Equilibrium distribution function
T_o, T₁:: Temperature given by T_c < T_o < T₁, T₁ < T
T:: Temperature at which polarons may first appear, the same at which hole or electron pairs are formed
W(k, k^′):: Probability of transition from k to k^′ in unit time
τ:: Relaxation time
ϵ₀:: Static dielectric constant
ϵ_∞:: High frequency dielectric constant
ϵ^*:: Effective dielectric constant
e:: The electron charge
e^*:: The neutral atom.

Conflict of Interests

The author declares that there is no conflict of interests regarding the publication of this paper.

References

1 Bednorz J. G. and Müller K. A., Possible high Tc superconductivity in the Ba-La-Cu-O system, Zeitschrift für Physik B. (1986) 64, no. 2, 189–193, 2-s2.0-30244454714, https://doi.org/10.1007/BF01303701.
10.1007/BF01303701
CAS Web of Science® Google Scholar
2 Sadovsky M. V., Models of the pseudogap state in high-temperature superconductors, http://arxiv.org/abs/cond-mat/0408489.
Google Scholar
3 Sica G., Samson G. H., and Alexandrov A. S., Pseudogap in high-temperature superconductors from realistic Fröhlich and Coulomb interactions, http://arxiv.org/abs/1208.0240.
Google Scholar
4 Kulic M. L., Electron phonon interaction and strong correlations in high-temperature superconductors: one can not avoid unavoidable, http://arxiv.org/abs/cond-mat/0404287.
Google Scholar
5 Alexandrov A. S. and Devreese J. T., Advances in Polaron Physics, 2010, Springer, Berlin, Germany.
10.1007/978-3-642-01896-1
Google Scholar
6 Maksimov E. G., The problem of high-temperature superconductivity. Present situation, Uspekhi Fizicheskikh Nauk. (2000) 170, 1033–1061.
10.3367/UFNr.0170.200010a.1033
Google Scholar
7 Plakida N. M., Spin excitations and mechanisms of superconductivity in cuprates, http://arxiv.org/abs/1110.6715.
Google Scholar
8 Bulut N., Scalapino D. J., and Scalettar R. T., Nodeless d-wave pairing in a two-layer Hubbard model, Physical Review B. (1992) 45, no. 10, 5577–5584, 2-s2.0-0001516867, https://doi.org/10.1103/PhysRevB.45.5577.
10.1103/PhysRevB.45.5577
CAS Web of Science® Google Scholar
9 Prelovsek P., Sega I., Ramsak A., and Bonca J., Spin fluctuations in cuprates as the key to high T_c, http://arxiv.org/abs/cond-mat/0601511.
Google Scholar
10 Bardeen J., Cooper L. N., and Schrieffer J. R., Theory of superconductivity, Physical Review. (1957) 108, no. 5, 1175–1204, 2-s2.0-0347190979, https://doi.org/10.1103/PhysRev.108.1175.
10.1103/PhysRev.108.1175
CAS Web of Science® Google Scholar
11 Muranaka T. and Akimitsu J., Superconductivity in MgB₂, Zeitschrift für Kristallographie. (2011) 226, no. 4, 385–394, 2-s2.0-79955748448, https://doi.org/10.1524/zkri.2011.1384.
10.1524/zkri.2011.1384
CAS Google Scholar
12 Gao M., Lu Z. Y., and Tao X., Prediction of phonon-mediated high temperature superconductivity in stoichiometric Li₂B₃C, http://arxiv.org/abs/1307.1323.
Google Scholar
13 Schrieffer J. R., Theory of Superconductivity, 1964, Benjamin, New York, NY, USA.
Google Scholar
14 Davydov A. S., Theoretical investigation of high-temperature superconductivity, Physics Report. (1990) 190, no. 4-5, 191–306, 2-s2.0-0000602249.
10.1016/0370-1573(90)90061-6
CAS Web of Science® Google Scholar
15 Crespi V. H. and Cohen M. L., Anharmonic phonons and high-temperature superconductivity, Physical Review B. (1993) 48, no. 1, 398–406, https://doi.org/10.1103/PhysRevB.48.398.
10.1103/PhysRevB.48.398
CAS Web of Science® Google Scholar
16 Mishenko A. S., Electron-phonon interaction in the undoped high temperature superconductors, Uspekhi Fizicheskikh Nauk. (2009) 179, 1259–1280.
10.3367/UFNr.0179.200912b.1259
Google Scholar
17 Landau L. D., E. M. Lifshitz, On the motion of electrons in a crystal lattice, Collection of Works of L.D. Landau, 1933, Nauka, Moscow, Russia.
Google Scholar
18 Anselm A. E., Introduction to Semiconductor Theory, 1978, Nauka, Moscow, Russia.
Google Scholar
19 Frohlich H., Interactions of electrons with lattice vibrations, Proceedings of the Royal Society A. (1952) 215, 291–298.
10.1098/rspa.1952.0212
CAS Web of Science® Google Scholar
20 Feynman R. P., Statistical Mechanics, 1972, Benjamin, New York, NY, USA.
Google Scholar
21 Zoli M., Polaron mass and electron-phonon correlations in the Holstein model, Advances in Condensed Matter Physics. (2010) 2010, 15, 815917, https://doi.org/10.1155/2010/815917.
10.1155/2010/815917
Web of Science® Google Scholar
22 Myasnikov E. N., Myasnikova A. E., and Kusmartsev F. V., Coherence of the lattice polarization in large-polaron motion, Physical Review B. (2005) 72, no. 22, 11, 2-s2.0-29644443064, https://doi.org/10.1103/PhysRevB.72.224303, 224303.
10.1103/PhysRevB.72.224303
Web of Science® Google Scholar
23 Davydov A. S. and Enolsky V. Z., Effective mass of the Pekar polaron, Zhurnal Eksperimental noi i Teoreticheskoi Fiziki. (1988) 94, 177–181.
Google Scholar
24 Devreese J. T., Polarons, http://arxiv.org/abs/cond-mat/0004497.
Google Scholar
25 Scalapino D. J., LohE.Jr., and Hirsch J. E., Fermi-surface instabilities and superconducting d-wave pairing, Physical Review B. (1987) 35, no. 13, 6694–6698, 2-s2.0-33749412417, https://doi.org/10.1103/PhysRevB.35.6694.
10.1103/PhysRevB.35.6694
CAS Web of Science® Google Scholar
26 Scalapino D. J., Superconductivity and spin fluctuations, http://arxiv.org/abs/cond-mat/9908287.
Google Scholar
27 Mahan G. D., Many-Particle Physics, 1990, Kluwer/Plenum, New York, NY, USA.
10.1007/978-1-4613-1469-1
Google Scholar
28 Kittel C., Quantum Theory of Solids, 1987, John Wiley & Sons, New York, NY, USA.
Google Scholar
29 Landau L. D. and Pekar S. I., E. M. Lifshitz and I. M. Khalatnikov, The effective mass of the polaron, Collected Works of L.D. Landau, 1948, 2, Nauka, Moscow, Russia, 47–53.
Google Scholar
30 Mourachkine A., Room Temperature Superconductivity, 2004, University of Cambridge, Cambridge, UK.
Google Scholar

All articles

The Role of Polarons in Cuprates Hi-T_c Superconductivity

Abstract

1. Introduction

2. Deformation Potential and Lattice Polarization

3. The c-Axis Polaron

4. Polaron Model of Hi-T_c Superconductivity

5. Conclusion

List of Symbols and Abbreviations

Conflict of Interests

References

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

The Role of Polarons in Cuprates Hi-Tc Superconductivity

Abstract

1. Introduction

2. Deformation Potential and Lattice Polarization

3. The c-Axis Polaron

4. Polaron Model of Hi-Tc Superconductivity

5. Conclusion

List of Symbols and Abbreviations

Conflict of Interests

References

Figures

References

Related

Information

The Role of Polarons in Cuprates Hi-T_c Superconductivity

4. Polaron Model of Hi-T_c Superconductivity