To make use of the sparsity property of broadband multipath wireless communication channels, we mathematically propose an l_p-norm-constrained proportionate normalized least-mean-square (LP-PNLMS) sparse channel estimation algorithm. A general l_p-norm is weighted by the gain matrix and is incorporated into the cost function of the proportionate normalized least-mean-square (PNLMS) algorithm. This integration is equivalent to adding a zero attractor to the iterations, by which the convergence speed and steady-state performance of the inactive taps are significantly improved. Our simulation results demonstrate that the proposed algorithm can effectively improve the estimation performance of the PNLMS-based algorithm for sparse channel estimation applications.

1. Introduction

Broadband signal transmission is becoming a commonly used high-data-rate technique for next-generation wireless communication systems, such as 3 GPP long-term evolution (LTE) and worldwide interoperability for microwave access (WiMAX) [1]. The transmission performance of coherent detection for such broadband communication systems strongly depends on the quality of channel estimation [2–5]. Fortunately, broadband multipath channels can be accurately estimated using adaptive filter techniques [6–10] such as the normalized least-mean-square (NLMS) algorithm, which has low complexity and can be easily implemented at the receiver. On the other hand, channel measurements have shown that broadband wireless multipath channels can often be described by only a small number of propagation paths with long delays [4, 11, 12]. Thus, a broadband multipath channel can be regarded as a sparse channel with only a few active dominant taps, while the other inactive taps are zero or close to zero. This inherent sparsity of the channel impulse response (CIR) can be exploited to improve the quality of channel estimation. However, such classical NLMS algorithms with a uniform step size across all filter coefficients have slow convergence when estimating sparse impulse response signals such as those in broadband sparse wireless multipath channels [11]. Consequently, corresponding algorithms have recently received significant attention in the context of compressed sensing (CS) [5, 12–14] and were already considered for channel estimation prior to the CS era [5, 12]. However, these CS channel estimation algorithms are sensitive to the noise in wireless multipath channels.

Inspired by the CS theory [12–14], several zero-attracting (ZA) algorithms have been proposed and investigated by combining the CS theory and the standard least-mean-square (LMS) algorithm for echo cancellation and system identification, which are known as the zero-attracting LMS (ZA-LMS) and reweighted ZA-LMS (RZA-LMS) algorithms, respectively [15]. Recently, this technique has been expanded to the NLMS algorithm and other adaptive filter algorithms to improve their convergence speed in a sparse environment [9, 16–18]. However, these approaches are mainly designed for nonproportionate adaptive algorithms. On the other hand, to utilize the advantages of the NLMS algorithm, such as stable performance and low complexity, the proportionate normalized least-mean-square (PNLMS) algorithm has been proposed and studied to exploit the sparsity in nature [19] and has been applied to echo cancellation in telephone networks. Although the PNLMS algorithm can utilize the sparsity characteristics of a sparse signal and obtain faster convergence at the initial stage by assigning independent magnitudes to the active taps, the convergence speed is reduced by even more than that of the NLMS algorithm for the inactive taps after the active taps converge. Consequently, several algorithms have been proposed to improve the convergence speed of the PNLMS algorithm [20–27], which include the use of the l₁-norm technique and a variable step size. Although these algorithms have significantly improved the convergence speed of the PNLMS algorithm, they still converge slowly after the active taps converge. In addition, some of them are inferior to the NLMS and PNLMS algorithms in terms of the steady-state error when the sparsity decreases. From these previously proposed sparse signal estimation algorithms, we know that the ZA algorithms mainly exert a penalty on the inactive channel taps through the integration of the l₁-norm constraint into the cost function of the standard LMS algorithms to achieve better estimation performance, while the PNLMS algorithm updates each filter coefficient with an independent step size, which improves the convergence of the active taps.

Motivated by the CS theory [13, 14] and ZA technique [15–18], we propose an l_p-norm-constrained PNLMS (LP-PNLMS) algorithm that incorporates the l_p-norm into the cost function of the PNLMS algorithm, resulting in an improved proportionate adaptive algorithm. The difference between the proposed LP-PNLMS algorithm and the ZA algorithms is that the gain-matrix-weighted l_p-norm is used in our proposed LP-PNLMS algorithm instead of the general l₁-norm to expand the application of ZA algorithms [15]. Also, this integration is equivalent to adding a zero attractor in the iterations of the PNLMS algorithm to obtain the benefits of both the PNLMS and ZA algorithms. Thus, our proposed LP-PNLMS algorithm can achieve fast convergence at the initial stage for the active taps. After the convergence of these active taps, the ZA technique in the LP-PNLMS algorithm acts as another force to attract the inactive taps to zero to arrest the slow convergence of the PNLMS algorithm. Furthermore, our proposed LP-PNLMS algorithm achieves a lower mean square error than the PNLMS algorithm and its related improved algorithms, such as the improved PNLMS (IPNLMS) [20] and μ-law PNLMS (MPNLMS) [21] algorithms. In this study, our proposed LP-PNLMS algorithm is verified over a sparse multipath channel by comparison with the NLMS, PNLMS, IPNLMS, and MPNLMS algorithms. The simulation results demonstrate that the LP-PNLMS algorithm achieves better channel estimation performance in terms of both convergence speed and steady-state behavior for sparse channel estimation.

The remainder of this paper is organized as follows. Section 2 briefly reviews the standard NLMS, PNLMS, and improved PNLMS algorithms, including the IPNLMS and MPNLMS algorithms. In Section 3, we describe in detail the proposed LP-PNLMS algorithm, which employs the Lagrange multiplier method. In Section 4, the estimation performance of the proposed LP-PNLMS algorithm is verified over sparse channels and compared with other commonly used algorithms. Finally, this paper is concluded in Section 5.

2. Related Channel Estimation Algorithms

2.1. Normalized Least-Mean-Square Algorithm

In this section, we first consider the sparse multipath communication system shown in Figure 1 to discuss the channel estimation algorithms. The input signal x(n) = [x(n), x(n − 1), …, x(n − N + 1)] ^T containing the N most recent samples is transmitted over a finite impulse response (FIR) channel with channel impulse response (CIR) h = [h₀, h₁, …, h_N−1] ^T, where (·)^T denotes the transposition operation. Then the output signal of the channel is written as follows:

(1)

where h is a sparse channel vector with K dominant active taps whose magnitudes are larger than zero and (N − K) inactive taps whose magnitudes are zero or close to zero with K ≪ N. To estimate the unknown sparse channel h, an NLMS algorithm uses the input signal x(n), the output signal y(n), and the instantaneous estimation error e(n), which is given by

(2)

where

is the NLMS adaptive channel estimator at instant n, d(n) = y(n) + v(n), and v(n) is an additive noise at the receiver. The update function of the NLMS channel estimation algorithm is expressed as

(3)

where μ_NLMS is the step size with 0 < μ_NLMS < 2 and δ_NLMS is a small positive constant used to avoid division by zero.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Typical sparse multipath communication system.

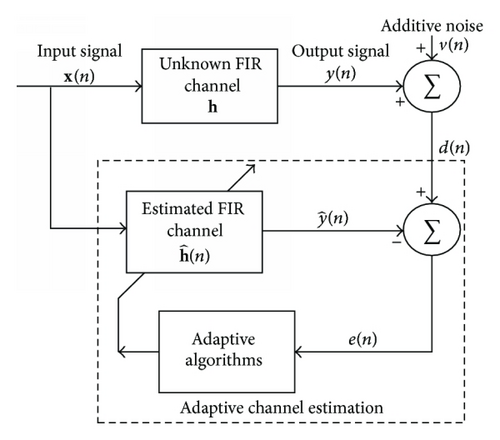
2.2. Proportionate Normalized Least-Mean-Square Algorithm

The PNLMS algorithm, which is an NLMS algorithm improved by the use of a proportionate technique, has been proposed for sparse system identification and echo cancellation. In this algorithm, each tap is assigned an individual step size, which is obtained from the previous estimation of the filter coefficient. According to the gain allocation rule in this algorithm, the greater the magnitude of the tap, the larger the step size assigned to it, and hence the active taps converge quickly. The update function of the PNLMS algorithm [19] is described by the following equation with reference to Figure 1:

(4)

Here, G(n), which denotes as the gain matrix, is a diagonal matrix that modifies the step size of each tap, μ_PNLMS is the global step size of the PNLMS algorithm, and

is a regularization parameter to prevent division by zero at the initialization stage, where

is the power of the input signal x(n). In the PNLMS algorithm, the gain matrix G(n) is given by

(5)

where the individual gain g_i(n) is defined as

(6)

with

(7)

where the parameters δ_p and ρ_g are positive constants with typical values of δ_p = 0.01 and ρ_g = 5/N. δ_p is used to regularize the updating at the initial stage when all the taps are initialized to zero, and ρ_g is used to prevent

from stalling when it is much smaller than the largest coefficient.

2.3. Improved Proportionate Normalized Least-Mean-Square Algorithms

2.3.1. IPNLMS Algorithm

The IPNLMS algorithm is a type of PNLMS algorithm used to improve the convergence speed of the PNLMS algorithm. It is a combination of the PNLMS and NLMS algorithms with the relative significance of each coefficient controlled by a factor α. The IPNLMS algorithm [20] adopts the l₁-norm to enable the smooth selection of (7), and the update equation of the IPNLMS algorithm is expressed as

(8)

where K(n) = diag⁡(k₀(n), k₁(n), …, k_N−1(n)) is a diagonal matrix used to adjust the step size of the IPNLMS algorithm, where

(9)

for a small positive constant ɛ and −1 ≤ α ≤ 1. At the initial stage, the step size is multiplied by (1 − α)/2N, since all the filter coefficients are initialized to zero. Thus, in the IPNLMS algorithm, a regularization parameter δ_IPNLMS is introduced, which is given by

(10)

We can see that the IPNLMS is identical to the NLMS algorithm for α = −1, while the IPNLMS behaves identically to the PNLMS algorithm when α = 1. In practical engineering applications, a suitable value for α is 0 or −0.5.

2.3.2. MPNLMS Algorithm

The μ-law PNLMS algorithm (MPNLMS) is another enhancement of the PNLMS algorithm that utilizes the logarithm of the magnitudes of the filter coefficients instead of using the magnitudes directly in the PNLMS algorithm [21]. The update equation is the same as that in the PNLMS algorithm given by (4). In the MPNLMS algorithm,

(11)

where

(12)

where ϑ is a large positive constant related to the estimation accuracy requirement, typically ϑ = 1000.

3. Proposed LP-PNLMS Algorithm

In this section, we propose an LP-PNLMS algorithm by incorporating the l_p-norm into the cost function of the PNLMS algorithm to create a zero attractor, making it a type of ZA algorithm. The difference between the LP-PNLMS algorithm and general ZA algorithms is that the gain-matrix-weighted l_p-norm is taken into account in designing the zero attractor. On the other hand, the proposed LP-PNLMS algorithm is based on the commonly used PNLMS algorithm, which is also a sparse channel estimation algorithm and can improve the convergence for the active taps. Regarding channel estimation, the purpose of the LP-PNLMS algorithm is to minimize

(13)

where G⁻¹(n) is the inverse of the gain matrix G(n) in the PNLMS algorithm, γ_LP > 0 is a very small constant used to balance the estimation error and the sparse l_p-norm penalty of

, ∥·∥_p is the p-norm defined as

, and 0 ≤ p ≤ 1. Note that in (13), we introduce an l_p-norm penalty to

after scaling the gain matrix by G⁻¹(n), which is different from the previously proposed ZA LMS algorithms.

To minimize (13), the Lagrange multiplier method is adopted, and the cost function J_LP(n + 1) of the proposed LP-PNLMS algorithm is expressed as

(14)

where λ is the Lagrange multiplier.

By calculating the gradient of the cost function J_LP(n + 1) of the LP-PNLMS algorithm and assuming

in the steady stage, we have

(15)

(16)

In practice, we need to introduce a small positive constant into the final term in (16) to cope with the situation that an entry of

approaches zero, which is the case for a sparse CIR at initialization. Then the update equation (16) of the LP-PNLMS algorithm is modified to

(17)

where ɛ_p is a small value to prevent division by zero. By multiplying both sides of (17) by x^T(n), we obtain

(18)

From (2), (15), and (17), we obtain

(19)

Then, the Lagrange multiplier λ is given as follows by solving (19):

(20)

Substituting (20) into (17), we have

(21)

It was found that the magnitudes of the elements in the matrix G(n)x(n)x^T(n){x^T(n)G(n)x(n)} ⁻¹ are much smaller than 1 for broadband multipath channel estimation. Therefore, the update equation (21) of the proposed LP-PNLMS algorithm is rewritten as

(22)

Here, we neglect the effects of the matrix G(n)x(n)x^T(n){x^T(n)G(n)x(n)} ⁻¹ and assume that the filter order is large. Similarly to the PNLMS algorithm, a step size μ_LP is introduced to balance the convergence speed and the steady-state error of the proposed LP-PNLMS algorithm, and a small positive constant

is employed to prevent division by zero. Thus, the update function (22) can be modified to

(23)

where ρ_LP = μ_LPγ_LP and

. Comparing the update function (23) of the proposed LP-PNLMS algorithm with the update function (4) of the PNLMS algorithm, we see that our proposed LP-PNLMS algorithm has the additional term γ_LPT(n), also defined as the zero attractor, which attracts the small channel taps to zero with high probability. Moreover, the ZA strength of this zero attractor is controlled by ρ_LP. In other words, in our proposed LP-PNLMS algorithm, the gain matrix G(n) assigns a large step size to the active channel taps of the sparse channel, while the zero attractor mainly exerts the l_p-penalty on the inactive taps whose taps are zero or close to zero. Thus, our proposed LP-PNLMS algorithm can further improve the convergence speed of the PNLMS algorithm after the convergence of the large active taps.

4. Results and Discussions

In this section, we present the results of computer simulations carried out to illustrate the channel estimation performance of the proposed LP-PNLMS algorithm over a sparse multipath communication channel and compare it with those of the previously proposed IPNLMS, MPNLMS, PNLMS, and NLMS algorithms. Here, we consider a sparse channel h whose length N is 64 or 128 and whose number of dominant active taps K is set to three different sparsity levels, namely, K = 2, 4 and 8, similar to previous studies [6, 22, 25, 26]. The dominant active channel taps are obtained from a Gaussian distribution with

, and the positions of the dominant channel taps are randomly spaced along the length of the channel. The input signal x(n) of the channel is a Gaussian random signal while the output of the channel is corrupted by an independent white Gaussian noise v(n). An example of a typical sparse multipath channel with a channel length of N = 64 and a sparsity level of K = 3 is shown in Figure 2. In the simulations, the power of the received signal is E_b = 1, while the noise power is given by

and the signal-to-noise ratio is defined as SNR =

. In all the simulations, the difference between the actual and estimated channels based on the sparsity-aware algorithms and the sparse channel mentioned above is evaluated by the MSE defined as follows:

(24)

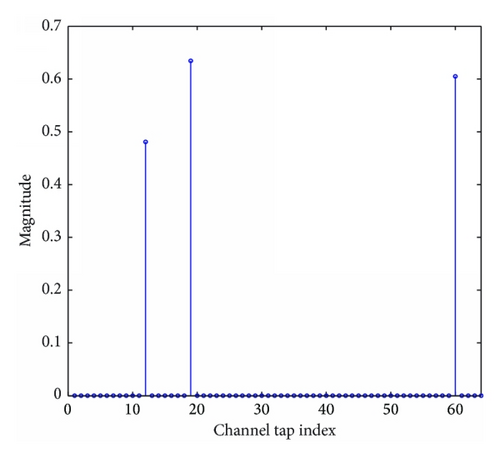
In these simulations, the simulation parameters are chosen to be μ_NLMS = μ_PNLMS = μ_IPNLMS = μ_LP = 0.5, δ_NLMS = 0.01, ɛ = 0.001, α = 0, ɛ_p = 0.05, ρ_LP = 1 × 10⁻⁵, δ_p = 0.01, ρ_g = 5/N, ϑ = 1000, p = 0.5, and SNR = 30 dB. When we change one of these parameters, the other parameters remain constant.

4.1. Estimation Performance of the Proposed LP-PNLMS Algorithm

4.1.1. Effects of Parameters on the Proposed LP-PNLMS Algorithm

In the proposed LP-PNLMS algorithm, there are two extra parameters, p and ρ_LP, compared with the PNLMS algorithm, which are introduced to design the zero attractor. Next, we show how these two parameters affect the proposed LP-PNLMS algorithm over a sparse channel with N = 64 or 128 and K = 4. The simulation results for different values of ρ_LP and p are shown in Figures 3 and 4, respectively. From Figure 3(a), we can see that the steady-state error of the LP-PNLMS algorithm decreases with decreasing ρ_LP when ρ_LP ≥ 2 × 10⁻⁶, while it increases again when ρ_LP is less than 2 × 10⁻⁶. Furthermore, the convergence speed of the LP-PNLMS algorithm rapidly decreases when ρ_LP is less than 1 × 10⁻⁵. This is because a small ρ_LP results in a low ZA strength, which consequently reduces the convergence speed. In the case of N = 128 shown in Figure 3(b), we observe that both the convergence speed and the steady-state performance are improved with decreasing ρ_LP for ρ_LP ≥ 1 × 10⁻⁵. When ρ_LP < 1 × 10⁻⁵, the convergence speed of the LP-PNLMS algorithm decreases while the steady-state error remains constant.

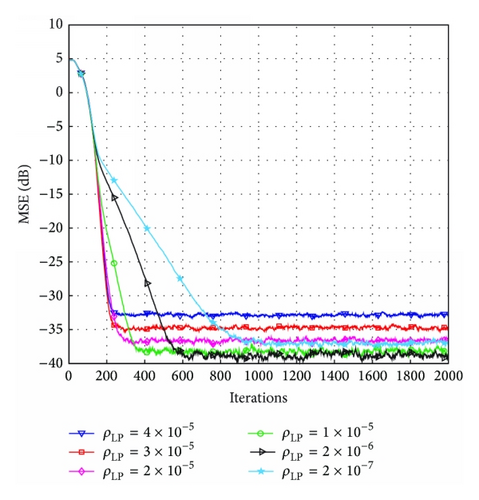
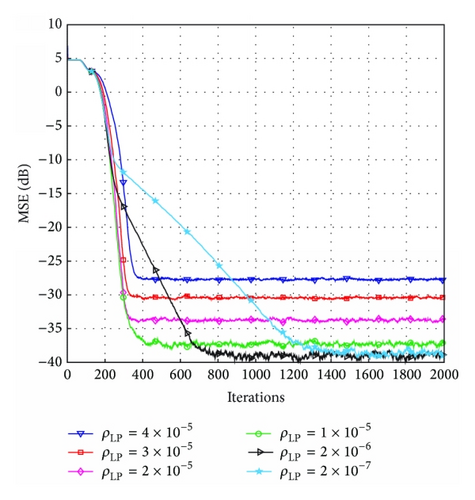
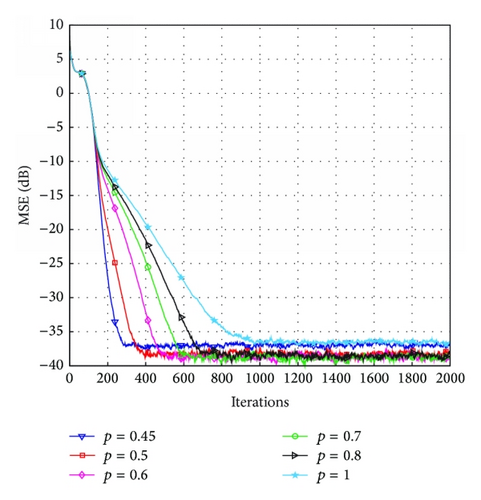
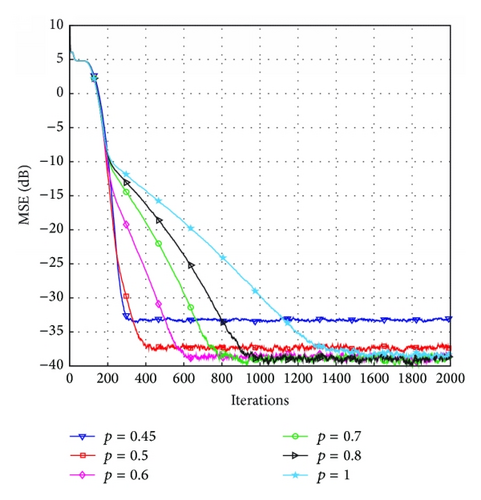
Figure 4 demonstrates the effects of the parameter p. We can see from Figure 4(a) that the convergence speed of the proposed LP-PNLMS algorithm rapidly decreases with increasing p for N = 64. Moreover, the steady-state error is reduced with p ranging from 0.45 to 0.5, while it remains constant for p = 0.6, 0.7, and 0.8. However, the steady-state performance for p = 1 is inferior to that for p = 0.8. This is because the proposed LP-PNLMS algorithm is an l₁-norm-penalized PNLMS algorithm, which cannot distinguish between active taps and inactive taps, reducing its convergence speed and steady-state performance. When N = 128, as shown in Figure 4(b), the steady-state performance is improved as p increases from 0.45 to 0.6. Thus, we should carefully select the parameters ρ_LP and p to balance the convergence speed and steady-state performance for the proposed LP-PNLMS algorithm.

4.1.2. Effects of Sparsity Level on the Proposed LP-PNLMS Algorithm

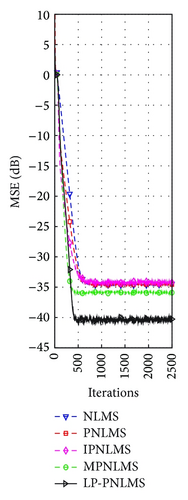
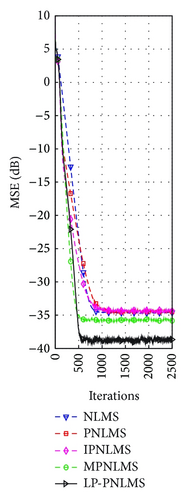
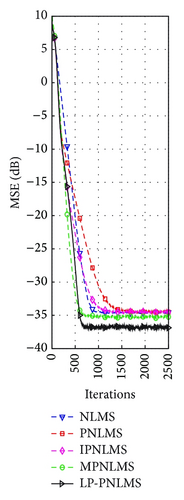
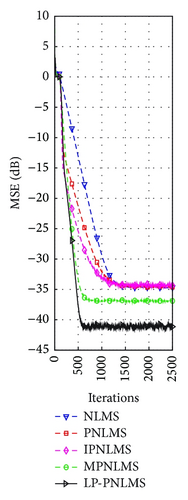
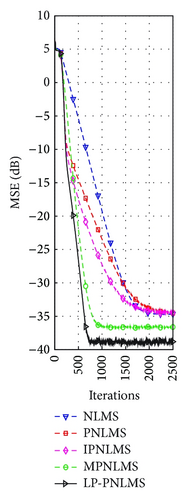
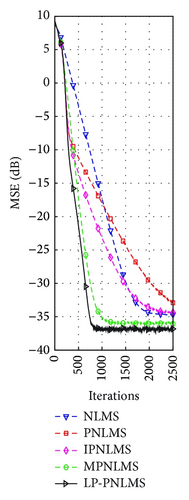
On the basis of the results discussed in Section 4.1.1 for our proposed LP-PNLMS algorithm, we choose p = 0.5 and ρ_LP = 1 × 10⁻⁵ to evaluate the channel estimation performance of the LP-PNLMS algorithm over a sparse channel with different channel lengths of N = 64 and 128, for which the obtained simulation results are given in Figures 5 and 6, respectively. From Figure 5, we see that our proposed LP-PNLMS algorithm has the same convergence speed as the PNLMS algorithm at the initial stage. The proposed LP-PNLMS algorithm converges faster than the PNLMS algorithm as well as the IPNLMS and NLMS algorithms for all sparsity levels K, while its convergence is slightly slower than that of the MPNLMS algorithm before it reaches a steady stage. However, the proposed LP-PNLMS algorithm has the smallest steady-state error for N = 64. When N = 128, we see from Figure 6 that our proposed LP-PNLMS algorithm not only has the highest convergence speed but also possesses the best steady-state performance. This is because with increasing sparsity, our proposed LP-PNLMS algorithm attracts the inactive taps to zero quickly and hence the convergence speed is significantly improved, while the previously proposed PNLMS algorithms mainly adjust the step size of the active taps and thus they only impact on the convergence speed at the early iteration stage. Additionally, we see from Figures 5 and 6 that both the convergence speed and the steady-state performance of all the PNLMS algorithms deteriorate when the sparsity level K increases for both N = 64 and 128. In particular, when K = 8, the convergence speeds of the PNLMS and IPNLMS algorithms are greater than that of the NLMS algorithm at the early iteration stage, while after this fast initial convergence, their convergence speeds decrease to less than that of the NLMS algorithm before reaching a steady stage. Furthermore, we observe that the MPNLMS algorithm is sensitive to the length N of the channel, and its convergence speed for N = 128 is less than that for N = 64 at the same sparsity level K and less than that of the proposed LP-PNLMS algorithm. Thus, we conclude that our proposed LP-PNLMS algorithm is superior to the previously proposed PNLMS algorithms in terms of both the convergence speed and the steady-state performance with the appropriate selection of the related parameters p and ρ_LP. From the above discussion, we believe that the gain-matrix-weighted l_p-norm method in the LP-PNLMS algorithm can be used to further improve the channel estimation performance of the IPNLMS and MPNLMS algorithms.

4.2. Computational Complexity

Finally, we discuss the computational complexity of the proposed LP-PNLMS algorithm and compare it with those of the NLMS, PNLMS, IPNLMS, and MPNLMS algorithms. Here, the computational complexity is the arithmetic complexity, which includes additions, multiplications, and divisions. The computational complexities of the proposed LP-PNLMS algorithm and the related PNLMS and NLMS algorithms are shown in Table 1.

Table 1. Computational complexity.

Algorithms	Additions	Multiplications	Divisions
NLMS	3N	3N + 1	1
PNLMS	4N + 3	6N + 3	N + 2
IPNLMS	4N + 7	5N + 5	N + 2
MPNLMS	5N + 3	7N + 3	N + 3
LP-PNLMS	4N + 4	9N + 4	2N + 2

From Table 1, we see that the computational complexity of our proposed LP-PNLMS algorithm is slightly higher than those of the MPNLMS and PNLMS algorithms, which is due to the calculation of the gradient of the l_p-norm. Furthermore, the MPNLMS algorithm has an additional logarithm operation, which increases its complexity but is not included in the Table 1. However, the LP-PNLMS algorithm noticeably increases the convergence speed and significantly improves the steady-state performance of the PNLMS algorithm. In addition, it also has a higher convergence speed and lower steady-state error than the IPNLMS and MPNLMS algorithms when the channel length is large.

5. Conclusion

In this paper, we have proposed an LP-PNLMS algorithm to exploit the sparsity of broadband multipath channels and to improve both the convergence speed and steady-state performance of the PNLMS algorithm. This algorithm was mainly developed by incorporating the gain-matrix-weighted l_p-norm into the cost function of the PNLMS algorithm, which significantly improves its convergence speed and steady-state performance. The simulation results demonstrated that our proposed LP-PNLMS algorithm, which has an acceptable increase in computational complexity, increases the convergence speed and reduces the steady-state error compared with the previously proposed PNLMS algorithms.

Conflict of Interests

The authors declare that there is no conflict of interests regarding the publication of this paper.

References

1 Korowajczuk L., LTE, WiMAX and WLAN Network Design, Optimization and Performance Analysis, 2011, John Wiley & Sons, New York, NY, USA.
10.1002/9781119970460
Google Scholar
2 Proakis J. G., Digital Communications, 2001, 4th edition, McGraw-Hill.
Google Scholar
3 Adachi F., Grag D., Takaoka S., and Takeda K., New direction of broadband CDMA techniques, Wireless Communications and Mobile Computing. (2007) 7, no. 8, 969–983.
10.1002/wcm.507
Web of Science® Google Scholar
4 Cotter S. F. and Rao B. D., Sparse channel estimation via matching pursuit with application to equalization, IEEE Transactions on Communications. (2002) 50, no. 3, 374–377, 2-s2.0-0036493737, https://doi.org/10.1109/26.990897.
10.1109/26.990897
Web of Science® Google Scholar
5 Bajwa W. U., Haupt J., Sayeed A. M., and Nowak R., Compressed channel sensing: a new approach to estimating sparse multipath channels, Proceedings of the IEEE. (2010) 98, no. 6, 1058–1076, 2-s2.0-77952743265, https://doi.org/10.1109/JPROC.2010.2042415.
10.1109/JPROC.2010.2042415
Web of Science® Google Scholar
6 Zayyani H., Babaie-Zadeh M., and Jutten C., Compressed sensing block MAP-LMS adaptive filter for sparse channel estimation and a Bayesian Cramer-Rao bound, IEEE International Workshop on Machine Learning for Signal Processing (MLSP’09), September 2009, Grenoble, France, 1–6, 2-s2.0-77950949315, https://doi.org/10.1109/MLSP.2009.5306268.
10.1109/MLSP.2009.5306268
Google Scholar
7 Rana Md. M., Kim J., and Cho W.-K., LMS based channel estimation of LTE uplink using variable step size and phase information, Radioengineering. (2010) 19, no. 4, 678–688, 2-s2.0-78650439982.
Web of Science® Google Scholar
8 Homer J., Mareels I., and Hoang C., Enhanced detection-guided NLMS estimation of sparse FIR-modeled signal channels, IEEE Transactions on Circuits and Systems I. (2006) 53, no. 8, 1783–1791, 2-s2.0-33747845020, https://doi.org/10.1109/TCSI.2006.879062.
10.1109/TCSI.2006.879062
Web of Science® Google Scholar
9 Babadi B., Kalouptsidis N., and Tarokh V., SPARLS: the sparse RLS algorithm, IEEE Transactions on Signal Processing. (2010) 58, no. 8, 4013–4025, 2-s2.0-77952558371, https://doi.org/10.1109/TSP.2010.2048103.
10.1109/TSP.2010.2048103
Web of Science® Google Scholar
10 Sayed A. H., Adaptive Filters, 2008, John Wiley & Sons.
10.1002/9780470374122
Google Scholar
11 Gui G. and Adachi F., Improved least mean square algorithm with application to adaptive sparse channel estimation, EURASIP Journal on Wireless Communications and Networking. (2013) 2013, article 204.
Google Scholar
12 Maechler P., Greisen P., Sporrer B., Steiner S., Felber N., and Burg A., Implementation of greedy algorithms for LTE sparse channel estimation, Conference Record of the Forty Fourth Asilomar Conference on Signals, Systems and Computers (ASILOMAR ′10), November 2010, Pacific Grove, Calif, USA, 400–405, 2-s2.0-79958002170, https://doi.org/10.1109/ACSSC.2010.5757587.
10.1109/ACSSC.2010.5757587
Google Scholar
13 Tibshirani R., Regression shrinkage and selection via the lasso, Journal of the Royal Statistical Society B. (1996) 58, no. 1, 267–288.
10.1111/j.2517-6161.1996.tb02080.x
Web of Science® Google Scholar
14 Donoho D. L., Compressed sensing, IEEE Transactions on Information Theory. (2006) 52, no. 4, 1289–1306, 2-s2.0-33645712892, https://doi.org/10.1109/TIT.2006.871582.
10.1109/TIT.2006.871582
Web of Science® Google Scholar
15 Chen Y., Gu Y., and HeroA. O.III, Sparse LMS for system identification, Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP ′09), April 2009, Taipei, Taiwan, 3125–3128, 2-s2.0-70349216427, https://doi.org/10.1109/ICASSP.2009.4960286.
10.1109/ICASSP.2009.4960286
Google Scholar
16 Taheri O. and Vorobyov S. A., Sparse channel estimation with L_P-norm and reweighted L₁ -norm penalized least mean squares, Proceedings of the 36th IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP ′11), May 2011, Prague, Czech Republic, 2864–2867, 2-s2.0-80051615550, https://doi.org/10.1109/ICASSP.2011.5947082.
10.1109/ICASSP.2011.5947082
Google Scholar
17 Gu Y., Jin J., and Mei S., ℓ0 norm constraint LMS algorithm for sparse system identification, IEEE Signal Processing Letters. (2009) 16, no. 9, 774–777, 2-s2.0-77949691635, https://doi.org/10.1109/LSP.2009.2024736.
10.1109/LSP.2009.2024736
Web of Science® Google Scholar
18 Das R. L. and Chakraborty M., A zero attracting proportionate normalized least mean square algorithm, Proceedings of the 2nd Asia-Pacific Signal and Information Processing Association Annual Summit and Conference (APSIPA ASC ′12), December 2012, Hollywood, Calif, USA, 1–4, 2-s2.0-79958133742.
Google Scholar
19 Duttweiler D. L., Proportionate normalized least-mean-squares adaptation in echo cancelers, IEEE Transactions on Speech and Audio Processing. (2000) 8, no. 5, 508–518, 2-s2.0-0034274237, https://doi.org/10.1109/89.861368.
10.1109/89.861368
Web of Science® Google Scholar
20 Benesty J. and Gay S. L., An improved PNLMS algorithm, Proceedings of the IEEE International Conference on Acoustic, Speech and Signal Processing, May 2002, Orlando, Fla, USA, 1881–1884, 2-s2.0-0036294060.
Google Scholar
21 Deng H. and Doroslovački M., Improving convergence of the PNLMS algorithm for sparse impulse response identification, IEEE Signal Processing Letters. (2005) 12, no. 3, 181–184, 2-s2.0-14644412385, https://doi.org/10.1109/LSP.2004.842262.
10.1109/LSP.2004.842262
Web of Science® Google Scholar
22 Khong A. W. H. and Naylor P. A., Efficient use of sparse adaptive filters, Proceedings of the 40th Asilomar Conference on Signals, Systems, and Computers (ACSSC ′06), November 2006, Pacific Grove, Calif, USA, 1375–1379, 2-s2.0-45749133051, https://doi.org/10.1109/ACSSC.2006.354982.
10.1109/ACSSC.2006.354982
Google Scholar
23 Liu L., Fukumoto M., Saiki S., and Zhang S., A variable step-size proportionate NLMS algorithm for identification of sparse impulse response, IEICE Transactions on Fundamentals of Electronics, Communications and Computer Sciences. (2010) 93, no. 1, 233–242, 2-s2.0-77950651508, https://doi.org/10.1587/transfun.E93.A.233.
10.1587/transfun.E93.A.233
Google Scholar
24 Nekuii M. and Atarodi M., A fast converging algorithm for network echo cancelation, IEEE Signal Processing Letters. (2004) 11, no. 4, 427–430, 2-s2.0-1942488901, https://doi.org/10.1109/LSP.2004.824027.
10.1109/LSP.2004.824027
Web of Science® Google Scholar
25 Liu L., Fukumoto M., and Saikfi S., An improved mu-law proportionate NLMS algorithm, Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP ′08), April 2008, Las Vegas, Nev, USA, 3797–3800, 2-s2.0-51449085663, https://doi.org/10.1109/ICASSP.2008.4518480.
10.1109/ICASSP.2008.4518480
Google Scholar
26 Paleologu C., Benesty J., and Ciochinǎ S., Sparse adaptive filters for echo cancellation, Synthesis Lectures on Speech and Audio Processing. (2010) 6, 1–124, 2-s2.0-77954945964, https://doi.org/10.2200/S00289ED1V01Y201006SAP006.
10.1007/978-3-031-02559-4
Google Scholar
27 Dogancay K., Partial-Update Adaptive Signal Processing: Design, Analysis and Implementation, 2008, Academic Press, Oxford, UK.
Google Scholar

Citing Literature

All articles

An Improved Proportionate Normalized Least-Mean-Square Algorithm for Broadband Multipath Channel Estimation

Abstract

1. Introduction

2. Related Channel Estimation Algorithms

2.1. Normalized Least-Mean-Square Algorithm

2.2. Proportionate Normalized Least-Mean-Square Algorithm

2.3. Improved Proportionate Normalized Least-Mean-Square Algorithms

2.3.1. IPNLMS Algorithm

2.3.2. MPNLMS Algorithm

3. Proposed LP-PNLMS Algorithm

4. Results and Discussions

4.1. Estimation Performance of the Proposed LP-PNLMS Algorithm

4.1.1. Effects of Parameters on the Proposed LP-PNLMS Algorithm

4.1.2. Effects of Sparsity Level on the Proposed LP-PNLMS Algorithm

4.2. Computational Complexity

5. Conclusion

Conflict of Interests

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley