The Dirichlet resonant boundary value problems are considered. If the respective nonlinear equation can be reduced to a quasilinear one with a nonresonant linear part and both equations are equivalent in some domain Ω and if solutions of the quasilinear problem are in Ω, then the original problem has a solution. We say then that the original problem allows for quasilinearization. If quasilinearization is possible for essentially different linear parts, then the original problem has multiple solutions. We give conditions for Emden-Fowler type resonant boundary value problem solvability and consider examples.

1. Introduction

Two-point nonlinear boundary value problems often appear in applications. Consider the following one. Let a nonlinear equation

(1)

be given together with the Dirichlet boundary conditions

(2)

The left hand side of the equation is the second order linear form

(3)

where p and q generally are continuous functions given in the interval [a, b]. The right side f is continuous. A solution x(t) is a function in C²[a, b]. Even equation of the form

(4)

and related boundary value problems are investigated insufficiently. The classical result says that the problem (4) and (2) is solvable if f is a bounded function. Otherwise various cases are possible. To reduce the problem to that with bounded right hand side the method of lower and upper functions can be used. This method is well developed and related descriptions and other information can be found in the books [1–4]. This method cannot be applied to equations which exhibit oscillatory behavior however. The lower and upper functions in case of the existence of a solution exist but coincide with a solution.

As to the problem (1) and (2) with a bounded function f, a similar result holds; namely, the problem (1) and (2) is solvable if the homogeneous problem

(5)

has only the trivial solution.

If this is not true the existence of a solution cannot be proved. There are examples, for instance, x^′′ + π²x = 1, x(0) = 0 and x(1) = 0 showing that a solution does not exist. This type of problems are called resonant problems.

There is an intensive literature on resonant problems. We mention several papers [5–13].

To treat resonant problems, various approaches were used. We focused on the quasilinearization method [14, 15], which consists in reducing the resonant problem to nonresonant one using suitable estimations of expected solutions.

Below we give a description of the quasilinearization method.

We consider the Dirichlet boundary value problem

(6)

(7)

where t ∈ I : = [a, b] and f ∈ C(I × ℝ², ℝ). The linear part of differential equation (6) (l₂x)(t): = x^′′ + p(t)x^′ + q(t)x is resonant with respect to given boundary conditions (7).

Definition 1. The linear part (l₂x)(t): = x^′′ + p(t)x^′ + q(t)x of differential equation (6) is called a nonresonant with respect to the boundary conditions (7) if the homogeneous problem

(8)

has only the trivial solution. Otherwise, if the homogeneous problem (8) has nontrivial solutions, then the linear part is called resonant.

For instance, x^′′ = 0 is nonresonant, but x^′′ + π²x = 0 is resonant in [0,1]; x^′′ + k²x = 0 is nonresonant with respect to the boundary conditions x(0) = x(1) = 0, if k ≠ πi, i = 0,1, …; that is, the coefficient k belongs to one of the intervals

(9)

These intervals are called nonresonant intervals.

The classical result states that the problem (6) and (7) is solvable if linear part (l₂x)(t) is nonresonant and f is continuous and bounded (the Picard theorem [3]). Therefore it is desirable to obtain the conditions for the boundary value problem (6) and (7) to be solvable for resonant linear parts.

In [16] the author considered the resonant boundary value problem (6) and (7) if f = f(t) and formulated the theorem that the problem (6) and (7) is solvable if

(10)

where α = −p/2,

, n is an integer, and p² − 4q < 0.

In one of the most popular articles on resonant problems [10] the authors considered the boundary value problem

(11)

Here h(t) ∈ L²([a, b]), α² is a constant, g : ℝ → ℝ is a continuous function, and the limits

(12)

exist and are finite.

In [10] the authors formulated the theorem that problem (11) has at least one solution if the inequalities

(13)

hold. This theorem is known as the Landesman-Lazer condition. Boundary value problem (11) has also been studied by Lazer [11], Alonso and Ortega [6], Ahmad [5], and Cesari and Kannan [7].

The function f in the Landesman-Lazer condition is of the specific form h(t) − g(u(t)). And it is an actual question to find the conditions ensuring that the problem (6) and (7) is solvable if f = f(t, x, x^′).

Our main result in this paper is to get conditions which guarantee that the resonant boundary value problem is solvable and we do not use the Landesman-Lazer condition.

We use the quasilinearization approach. This approach was developed in [14, 15]. Using this approach we reduce (6) to a quasilinear one of the form

(14)

where a function F is continuous and bounded by a constant M and the linear part (L₂x)(t) is nonresonant yet with respect to the given boundary conditions (7) that means that the respective homogeneous problem

(15)

has only the trivial solution.

If such reduction is possible then according to Conti′s theorem [17] the modified problem (14) and (7) is solvable.

If a solution x(t) of the modified quasilinear problem (14) and (7) is located in the domain Ω(t, x, x^′), where both (6) and (14) are equivalent, then the original problem (6) and (7) at resonance has a solution.

Our paper consists of the introduction, four sections, conclusions and references.

Definitions of the type of a solution to Dirichlet boundary value problems are given in Section 2. The general result and related auxiliary results for quasilinear problems are stated.

In Section 3 we describe quasilinearization process and formulate and prove the theorem for resonant boundary value problem (6) and (7) to be solvable.

In Section 4 the idea of quasilinearization is applied to the investigation of the Emden-Fowler type resonant boundary problem.

In Section 5 we consider an example.

2. Auxiliary Results

We consider quasilinear problem (14) and (7).

Theorem 2 (see [17].)If F(t, x, x^′) in (14) is a continuous and bounded function and the homogeneous problem (15) has only the trivial solution, then the problem (14) and (7) is solvable.

The solution of quasilinear problem (14) and (7) can be written in the integral form

(16)

Respectively,

(17)

where G(t, s) is the Green function for the respective homogeneous problem (15).

If |F(t, x, x^′)| ≤ M∀(t, x, x^′) ∈ I × ℝ², then from (16) and (17) it follows that

(18)

where Γ and Γ₁ are bounds for |G(t, s)| and |(∂/∂t)G(t, s)|, respectively.

For instance, if the linear part is (L₂x)(t): = x^′′ + k²x then Green′s function for Dirichlet problem (15) in the interval [0,1] is given by

(19)

and satisfies the estimates

(20)

Definition 3 (see [14], [15].)We will say that the linear part (L₂x)(t) is i-nonresonant with respect to the boundary conditions (7), if a solution x(t) of the Cauchy problem

(21)

has exactly i zeros in the interval (a, b) and x(b) ≠ 0.

Definition 4 (see [14], [15].)We will say that ξ(t) is an i-type solution of the problem (6) and (7) (resp., (14) and (7)) if for small enough r > 0 the difference u(t; r) = x(t; r) − ξ(t) has exactly i zeros in (a, b) and u(b; r) ≠ 0, where x(t; r) is a solution of (6) (resp., (14)), which satisfies the initial conditions

(22)

Theorem 5 (see [15], Theorem 2.1.)Quasilinear problem (14) and (7) with an i-nonresonant linear part (L₂x)(t) has an i-type solution.

The proof can be found in [14, 15].

Definition 6. Let (6) and (14), where the linear part (L₂x)(t) is nonresonant with respect to the boundary conditions (7) in the interval I, be equivalent in the domain

(23)

in the sense that any solution x : I → ℝ of (6) with a graph in Ω₁ is also a solution of (14) and vice versa. Suppose that any solution x(t) of the quasilinear problem (14) and (7) satisfies the estimates

(24)

We will say then that the problem (6) and (7) allows for quasilinearization with respect to a domain Ω₁ and a linear part (L₂x)(t).

The following results in [14, 15] form a basis for application of the quasilinearization process for proving the existence of multiple solutions.

Theorem 7 (see [14], [15].)If the problem (6) and (7) allows for quasilinearization with respect to some domain Ω₁ and some i-nonresonant linear part (L₂x)(t), then it has an i-type solution.

Theorem 8 (see [14], [15].)Suppose that the problem (6) and (7) allows for quasilinearization with respect to Ω₁ and i-nonresonant linear part (L₂x)(t), and, at the same time, it allows for quasilinearization with respect to a domain

(25)

and j-nonresonant linear part

, where i ≠ j. Then the problem (6) and (7) has at least 2 solutions of different types.

Corollary 9. Suppose that the problem (6) and (7) allows for quasilinearization with respect to n essentially different (in the sense of Definition 3) linear parts and n domains of the form (23). Then it has at least n different solutions.

3. Preliminary Results

We consider the resonant problem (6) and (7), where f(t, x, x^′) is continuous function and the linear part (l₂x)(t) is resonant.

We use quasilinearization process as follows.

(1)
First we modify the equation adding a linear part so that the resulting linear part is not resonant yet
(26)
(2)
We choose constants N > 0 and N₁ > 0 and truncate right side:
(27)
where
(28)
(3)
We check the inequalities
(29)
where Γ and Γ₁ are the estimates of Green′s function and its derivative associated with the linear part in (27); .

Theorem 10. Suppose that ɛ², N and N₁ as above can be found such that the inequalities

(30)

(31)

are fulfilled.

Then the problem (6) and (7) has a solution such that |x(t)| ≤ N ∀t ∈ [a, b] and |x^′(t)| ≤ N₁∀t ∈ [a, b].

Proof. Apply (26) and (27). From Theorem 2 the boundary value problem (27) and (7) is solvable and has a solution x(t), which can be written in the integral form using Green′s function.

The inequalities (30) and (31) are fulfilled. This means that

(32)

For these values of x and x^′ the original equation (6) and the modified equation (27) are equivalent:

(33)

It follows that x(t) is also a solution of the original problem (6) and (7).

Remark 11. If the right side in (6) does not depend on x^′, then N₁ can be set to +∞ and therefore only inequality (30) should be verified.

4. Application: Emden-Fowler Type Equation

Consider the Emden-Fowler type resonant problem

(34)

(35)

Theorem 12. Suppose that

(36)

and inequality

(37)

holds for some

, (i = 1,2, …), where β > 1 is the root of the equation

(38)

Then there exists an i-type solution of the problem (34) and (35).

Proof. Let us consider instead of (34) the equivalent one

(39)

The linear part (L₂x)(t) = x^′′ + (π²(4 + k²)/4)x is nonresonant with respect to the boundary conditions (35) if

, where i is an integer. We wish to make the right side in (39) bounded. Denote

(40)

The function f_k(t, x) is odd in x for fixed t. Consider it for nonnegative values of x. There exists point of local extremum x₀ (it is either a point of maximum in case of p > 1 or a point of minimum in case of 0 < p < 1):

(41)

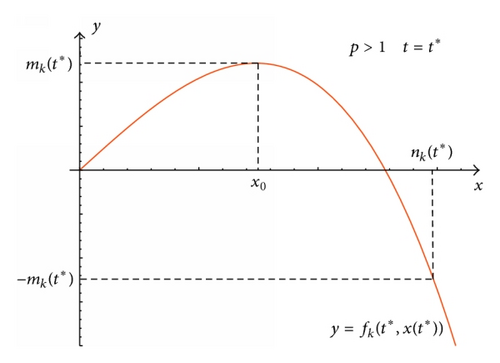
Figure 1 illustrates the case of p > 1 for fixed t = t^*.

We can calculate the value of the function at the point of maximum x₀. Set

(42)

Choose n_k(t) such that

(43)

The value of n_k(t) is computed by solving the equation

(44)

or, equivalently, that of

(45)

with respect to x for any fixed t. Computation gives that

(46)

where a constant β > 1 is described in (38). Set

(47)

Let us consider the quasilinear equation

(48)

where F_k(t, x) = f_k(t, δ(−N_k, x, N_k)).

The modified quasilinear equation (48) is equivalent to the given equation (34) in the respective domains

(49)

The problem (48) and (35) is solvable and solutions can be written in integral form

(50)

where G_k(t, s) is the Green function to the respective homogeneous problem

(51)

It is given by

(52)

and satisfies the estimate

(53)

It follows from (50) that

(54)

If inequality

(55)

holds, then a solution x(t) of the quasilinear problem (48) and (35) satisfies the estimate

(56)

and the original problem (34) and (35) allows for quasilinearization with respect to the domain Ω_k and the linear part (L₂x)(t): = x^′′ + (π²/4)(4 + k²)x. It follows from Theorem 5 that if the linear part (L₂x)(t) is i-nonresonant, then the problem (34) and (35) has an i-type solution.

Then k should satisfy the inequalities

(57)

(58)

where i = 1,2, ….

Consider inequality (55) and assume that q(t) satisfies the estimates (36). If p > 1, then

(59)

but in the case of 0 < p < 1 we have

(60)

Hence inequality (55) reduces to (37).

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Existence of a number n_k.

We have computed results (see Table 1) for q = 1, various p, which show that some k² satisfy inequality (37). It may happen that several k fall into the same nonresonance interval . In Table 1 we select only one k for any respective nonresonance interval (this prevents an error when estimating the number of solutions of different types). For instance, in the case p = 3/2, two values of k, namely, k = 1 and k = 3, fall into the same nonresonance interval . We show only k = 1 in Table 1. Intervals of nonresonance are given in the third column of Table 1.

Table 1. Results of calculations for the boundary value problem x^′′ + π²x = −|x|^psign⁡x, x(0) = 0 = x(1).

p	i	k	ΓM_k	N_k
3	1	1	1.172	1.814

2	1	1	1.196	2.978

3/2	1	1	1.748	7.616

4/3	1	1	3.071	19.083
	2	5	219478	298164
	3	7	2.178 · 10⁶	2.245 · 10⁶

5/4	1	1	5.886	47.492
	2	5	1.052 · 10⁷	1.855 · 10⁷
	3	7	2.045 · 10⁸	2.738 · 10⁸
	4	9	1.917 · 10⁹	2.044 · 10⁹

6/5	1	1	11.875	117.828
	2	5	5.304 · 10⁸	11.507 · 10⁸
	3	7	2.021 · 10¹⁰	3.328 · 10¹⁰
	4	9	3.132 · 10¹¹	4.108 · 10¹¹
	5	11	2.813 · 10¹²	3.056 · 10¹²

5/6	1	1	0.00148	0.00601
	2	5	1.078 · 10⁻¹¹	2.460 · 10⁻¹¹
	3	7	2.506 · 10⁻¹³	4.339 · 10⁻¹³
	4	9	1.541 · 10⁻¹⁴	2.127 · 10⁻¹⁴
	5	11	1.675 · 10⁻¹⁵	1.914 · 10⁻¹⁵

4/5	1	1	0.0017	0.0149
	2	5	8.132 · 10⁻¹⁰	15.264 · 10⁻¹⁰
	3	7	3.706 · 10⁻¹¹	5.277 · 10⁻¹¹
	4	9	3.767 · 10⁻¹²	4.275 · 10⁻¹²

3/4	1	1	0.0055	0.0371
	2	5	6.459 · 10⁻⁸	9.502 · 10⁻⁸
	3	7	5.768 · 10⁻⁹	6.439 · 10⁻⁹

2/3	1	1	0.0191	0.0931

1/6	1	1	0.382	0.566

Example 13. For instance, we consider the resonant equation

(61)

with boundary conditions (35).

Function −|x|³sign⁡x is odd. And for x > 0 we can rewrite

(62)

Rewrite (62) equivalently:

(63)

The linear part in (63) is no more resonant with respect to (35).

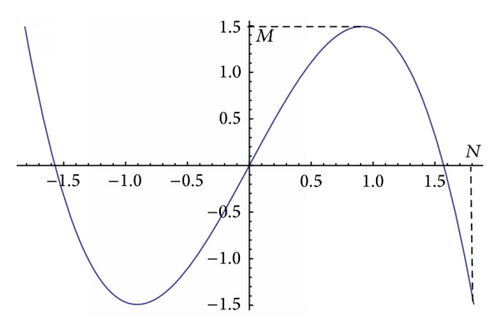
We would like to make the function f(x): = (π²/4)x − x³ bounded and still continuous. The function f(x) is an odd function with a maximum at (cf. Figure 2). Define . Solve the equation f(x) = −M for x > 0. The solution is .

Define the truncated function

(64)

In this example it is

(65)

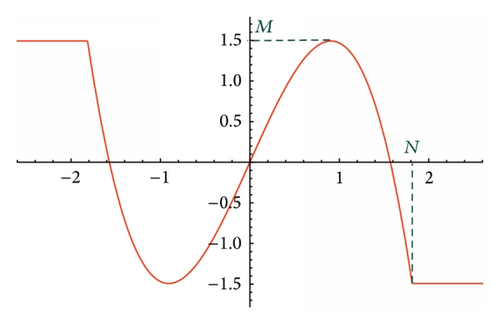
The function F(x) is continuous and bounded by the number M (cf. Figure 3). Therefore the problem

(66)

has a solution x(t). Let us show that |x(t)| ≤ N ∀t ∈ [0,1] and hence x(t) is also a solution of the problem (61) and (35).

A solution x(t) of (66) satisfies the integral equation

(67)

where G is the Green function for the problem

(68)

It follows from (67) that

(69)

where

, holds.

Then,

(70)

satisfies, since

(71)

This means that the problem (61) allows for quasilinearization with respect to the linear part (L₂x)(t): = x^′′ + (π²/4)(4 + k²)x, where k = 1 and one can only propose that there exists 1-type solution.

The problem

(72)

allows for three essentially different quasilinearizations with k = 1, 5 and 7. Then there exist at least 3 solutions of different types. First, it has the trivial solution, which is a 1-type solution. Figure 4 illustrates the 2-type and 3-type solutions of the boundary value problem (72).

5. Example: Equation x^′′ + π²x = −x⁷ + x⁵ − x³

We consider the boundary value problem

(73)

Similar to the previous example we rewrite the equation equivalently:

(74)

The function f(t): = −x⁷ + x⁵ − x³ + (π²/4)x is odd and we would like to make this function bounded and still continuous. The function f(x) has a maximum at x ≈ 0.871975. Define M : = f(0.871975) ≈ 1.60933. Solve the equation f(x) = −M for x > 0. The solution is N : ≈1.30261.

We define the truncated function

(75)

which is bounded and continuous. The quasilinear boundary value problem

(76)

has a solution x(t). We can write it through Green′s function, where the estimate of Green′s function is

(77)

Therefore,

(78)

This means that for this example the problem (73) allows for quasilinearization with respect to the linear part (L₂x)(t): = x^′′ + (π²/4)(4 + k²)x, where k = 1. Using quasilinearization process we can say that resonant boundary problem (73) is solvable.

6. Conclusions

We show that the resonant boundary value problem can be studied by using a quasilinearization process. The respective cases are considered, when the differential equations of resonant type with bounded or unbounded right side function allow for quasilinearization. As an application the conditions for solvability of the Emden-Fowler type resonant boundary value problem are given. Two examples are considered in detail showing the quasilinearization approach in action. By using quasilinearization process with different linear parts we can state the existence of different solutions of a problem thus obtaining multiplicity of results.

Conflict of Interests

The author declares that there is no conflict of interests regarding the publication of this paper.

References

1 Bernfeld S. R. and Lakshmikantham V., An Introduction to Nonlinear Boundary Value Problems, 1974, Academic Press, New York, NY, USA, MR0445048.
Google Scholar
2 de Coster C. and Habets P., Two-Point Boundary Value Problems: Lower and Upper Solutions, 2006, Elsevier, Oxford, UK, MR2225284.
Google Scholar
3 Kelley W. G. and Peterson A. C., The Theory of Differential Equations, 2004, Pearson Prentice Hall, Upper Saddle River, NJ, USA, MR2640364.
Google Scholar
4 Klokov Y. A. and Vasilyev N. I., Fundamentals of the Theory of Boundary Value Problems of Ordinary Differential Equations, Zinatne, Riga, Latvia, 1978 (Russian).
Google Scholar
5 Ahmad S., A resonance problem in which the nonlinearity may grow linearly, Proceedings of the American Mathematical Society. (1984) 92, no. 3, 381–384, https://doi.org/10.2307/2044839, MR759657.
10.1090/S0002-9939-1984-0759657-9
Google Scholar
6 Alonso J. M. and Ortega R., Unbounded solutions of semilinear equations at resonance, Nonlinearity. (1996) 9, no. 5, 1099–1111, https://doi.org/10.1088/0951-7715/9/5/003, MR1416469, ZBL0896.34026.
Google Scholar
7 Cesari L. and Kannan R., Existence of solutions of a nonlinear differential equation, Proceedings of the American Mathematical Society. (1983) 88, no. 4, 605–613, https://doi.org/10.2307/2045447, MR702284, ZBL0529.34005.
Google Scholar
8 Iannacci R. and Nkashama M. N., Nonlinear two-point boundary value problems at resonance without Landesman-Lazer condition, Proceedings of the American Mathematical Society. (1989) 106, no. 4, 943–952, https://doi.org/10.2307/2047278, MR1004633, ZBL0684.34025.
Google Scholar
9 Kannan R., Nieto J. J., and Ray M. B., A class of nonlinear boundary value problems without Landesman-Lazer condition, Journal of Mathematical Analysis and Applications. (1985) 105, no. 1, 1–11, https://doi.org/10.1016/0022-247X(85)90093-9, MR773569, ZBL0589.34013.
10.1016/0022-247X(85)90093-9
Google Scholar
10 Landesman E. M. and Lazer A. C., Nonlinear perturbations of linear elliptic boundary value problems at resonance, Journal of Applied Mathematics and Mechanics. (1970) 19, 609–623, MR0267269.
Google Scholar
11 Lazer A. C., A second look at the first result of Landesman-Lazer type, Electronic Journal of Differential Equations. (2000) 5, 113–119.
Google Scholar
12 Sveikate N., Quasilinearization for resonant boundary value problems with Neumann boundary conditions, Proceedings of IMCS of University of Latvia. (2013) 13, 110–119.
Google Scholar
13 Yermachenko I., Two-point boundary value problems at resonance, Mathematical Modelling and Analysis. (2009) 14, no. 2, 247–257, https://doi.org/10.3846/1392-6292.2009.14.247-257, MR2535856, ZBL1180.34017.
Web of Science® Google Scholar
14 Yermachenko I. and Sadyrbaev F., Quasilinearization and multiple solutions of the Emden-Fowler type equation, Mathematical Modelling and Analysis. (2005) 10, no. 1, 41–50, MR2129748, ZBL1084.34020.
10.3846/13926292.2005.9637269
Google Scholar
15 Yermachenko I. and Sadyrbaev F., Types of solutions and multiplicity results for two-point nonlinear boundary value problems, Nonlinear Analysis: Theory, Methods and Applications. (2005) 63, no. 5–7, e1725–e1735, 2-s2.0-28044443891, https://doi.org/10.1016/j.na.2004.12.035.
Google Scholar
16 Sveikate N., Remarks on resonant problems, Proceedings of IMCS of University of Latvia. (2012) 12, 43–53.
Google Scholar
17 Conti R., Equazioni differenziali ordinarie quasilineari con condizioni lineari, Annali di Matematica Pura ed Applicata. (1962) 57, no. 1, 49–61, MR0141841, https://doi.org/10.1007/BF02417726, ZBL0105.29402.
Google Scholar

Citing Literature

All articles

Resonant Problems by Quasilinearization

Abstract

1. Introduction

2. Auxiliary Results

3. Preliminary Results

4. Application: Emden-Fowler Type Equation

5. Example: Equation x^′′ + π²x = −x⁷ + x⁵ − x³

6. Conclusions

Conflict of Interests

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Resonant Problems by Quasilinearization

Abstract

1. Introduction

2. Auxiliary Results

3. Preliminary Results

4. Application: Emden-Fowler Type Equation

5. Example: Equation x′′ + π2x = −x7 + x5 − x3

6. Conclusions

Conflict of Interests

References

Citing Literature

Figures

References

Related

Information

5. Example: Equation x^′′ + π²x = −x⁷ + x⁵ − x³