This paper presents optimum design of time-censored constant-stress partially accelerated life test sampling plan (PALTSP) in which each item runs either at use or at accelerated conditions and product life follows Burr type XII. The optimal plan consists in finding out sample proportions allocated to both use and accelerated conditions by minimizing the asymptotic variance of test statistic for deciding on acceptance/rejection of the lot such that producer’s and consumer’s interests are safeguarded. The method developed has been illustrated using an example. Sensitivity analysis has also been carried out.

1. Introduction

Quality control methods are commonly used to determine the acceptability of a product with regard to its usefulness at the time it is put into the service. Reliability is related to the concept of quality of performance. Achieving desirable standards of reliability requires careful analysis in the product design phase. Analysis of data, obtained on a timely basis during product performance, keeps the design and production parameters updated and ensures that the product continues to perform in an acceptable manner. Reliability is built in through quality of design.

Acceptance sampling plans (ASPs) are commonly used to determine the acceptability of a product. If the sample data are related to the reliability of items (e.g., lifetimes or number of failures), then the corresponding ASP is called life test sampling plan or reliability acceptance sampling plan.

Many modern high reliability products are designed to operate without failure for a very long time. Life testing for these products under normal operating conditions is time consuming as it takes a lot of time to obtain reasonable failure information. Introducing ALT in life test sampling plan can be a good way to overcome such a difficulty. This has necessitated the formulation of ALTSPs. ALTSPs differ in the assumed life distribution, censoring schemes, failure monitoring method, test condition, and so forth.

Life test under accelerated environmental conditions may be fully accelerated or partially accelerated. In fully accelerated life testing all the test units are run at accelerated condition, while in partially accelerated life testing they are run at both normal and accelerated conditions. Commonly used stress loadings are constant-stress and step-stress (see Nelson [1]). Under constant-stress PALT each item is tested either at normal operating condition or at accelerated condition only. However, in step-stress PALT, a test item is first run at normal operating condition and, if it does not fail then, it is run at accelerated condition until failure occurs or the observation is censored. Accelerated test condition includes stresses in the form of temperature, voltage, pressure, vibration, cycling rate, humidity, and so forth.

Several authors have studied the problem of designing PALT under constant-stress loading. Yang [2] has indicated that constant-stress accelerated life tests are widely used to save time and money. DeGroot and Goel [3] have considered a PALT and estimated the parameters of the exponential distribution and the acceleration factor using the Bayesian approach. Bai et al. [4] have used the maximum likelihood method to estimate the scale parameter and the acceleration factor for the log normally distributed lifetime, using type I censoring data. Ismail [5] has used maximum likelihood and Bayesian methods for estimating the acceleration factor and the parameters of Pareto distribution of the second kind. Also, Bhattacharyya and Soejoeti [6] have estimated the parameters of the Weibull distribution and acceleration factor using maximum likelihood method. Bai and Chung [7] have considered optimal designs for both constant and step PALTs under type I censoring. Abdel-Hamid [8] has used the constant-stress PALT and estimated the parameters of the Burr type XII distribution and the acceleration factor under progressive type II censoring

However, no work seems to exist in the literature with PALT incorporated in acceptance sampling plan to facilitate formulation of decision rules for accepting or rejecting a lot of high reliability items satisfying producer’s and consumer’s requirements. In this paper optimum time-censored constant-stress PALT sampling plans have been designed using hazard acceleration and the Burr type XII life distribution. Single sample acceptance sampling plans by variables are used, and acceptance/rejection decision of a lot is based on Schneider’s [9] approach to k-method wherein sample mean and standard deviation are replaced by MLEs of location parameter and scale parameter of log life distribution, respectively. The asymptotic variance of the test statistic so obtained is used for deciding on lot disposition. The optimal plan consists in finding out sample proportions allocated to both use and accelerated conditions for the constant PALT by minimizing the asymptotic variance of test statistic for deciding on acceptance/rejection of the lot such that producer’s and consumer’s interests are safeguarded.

2. Model Assumptions and Test Procedure

2.1. Assumptions

(a)
The lifetime of an item tested either at normal operating condition or at accelerated conditions follows Burr type XII distribution.
(b)
The lifetimes of test units are independent and identically distributed random variables.
(c)
Tampered failure rate (TFR) model is assumed (Bhattacharyya and Soejoeti [6]).
(d)
The log-lifetimes T_i, i = 1,2, …, nϕ₁, of items allocated to normal operating condition and the log-lifetimes T_1j, j = 1,2, …, nϕ₂, and T_2j, j = 1,2, …, nϕ₃, of items allocated to accelerated conditions are mutually independent.

2.2. Test Procedure

(a)
The test is conducted with three test chambers, namely, one in which items are tested at normal operating condition, the second in which acceleration factor, A₁, is applied to the test items, and the third in which acceleration factor, A₂, is applied to the test items. Out of total “n” items, “nϕ₁” items randomly chosen are allocated to normal operating condition, “nϕ₂” items are allocated to first accelerated condition, A₁, and the remaining “nϕ₃” items are allocated to second accelerated condition, A₂, ϕ₁ + ϕ₂ + ϕ₃ = 1.
(b)
The test is continued until
- (i)
  failure of all test items, or
- (ii)
  a prescribed censoring time η

whichever occurs earlier, and the test condition should remain the same.

3. Burr Type XII Life Distribution

The Burr type XII distribution has a nonmonotone hazard function, which can accommodate many shapes of hazard function.

The pdf and cdf, respectively, of Burr type XII distribution are

()

where c and k are shape parameters and α is a scale parameter. The Burr (c, k, α) is unimodal, and its mode is Y_mode = α((c−1)/(ck + 1))^1/c if c > 1 and the pdf is L-shaped if c ≤ 1.

The reliability function and hazard rate function are given by

()

The exponential distribution follows from Burr type XII distribution as k → ∞, such that α = k^1/2 and c = 1. The Weibull life distribution also follows from Burr type XII distribution as k → ∞, such that α = k^1/2. For k = 1, the Burr type XII distribution reduces to log-logistic distribution.

4. Tampered Failure Rate Model

Bhattacharyya and Soejoeti [6] have proposed the TFR model for step-stress PALT. Their model assumes that a change in the stress has a multiplicative effect on the failure rate function over the remaining life. In this paper TFR model has been used in constant-stress PALT. Consider a constant-stress PALT wherein a test unit is tested either under use condition or under accelerated conditions till the censoring time. Let there be (m + 1) test chambers in all including one in which the items are tested under normal operating condition. The TFR model assumes that the effect of changing acceleration factor A_i−1 in (i − 1)th test chamber to A_i in ith test chamber is to multiply the failure rate function h_i−1(y) by A_i, i = 1,2, …, m. Thus, the effect of changing stress through acceleration factor in different test chambers has multiplicative effect on initial failure rate function. Hence, the tampered failure rate model is given by

()

where A_i > 1 ∀ i = 1,2, …, m.

Unlike fully accelerated life testing wherein a regression structure on the stress variable (e.g., temperature and voltage) is specified, the acceleration factor A_i, i = 1,2, …, m, is assumed to be a parameter of the model in PALT.

Let

; then (4a) can be rewritten as

()

where

. Thus, h(y) < h₁(y) < h₂(y) < ⋯<h_m(y).

4.1. Life Distribution under TFR Model

Therefore, the pdf and cdf of TFR model when underlying life distribution is Burr type XII are given by

()

In this paper, we have taken three test chambers; that is, m + 1 = 3.

5. Lot Acceptance Sampling Procedure

Assume that one-sided lower specification limit L exists for the lifetime of a product. Let for convenience T = ln⁡Y, instead of using the actual life time Y. The lower specification limit on T is L^′ = ln⁡L. Then, pdf and cdf of an item tested at normal operating condition and at accelerated conditions using g_Y(y),

, G_Y(y), and

in Section 4.1 are given by

()

The reliability function of an item tested at normal and accelerated conditions

and

are, respectively, given by

()

where μ = ln⁡(α) is location parameter and σ = (c)⁻¹.

The following lot acceptance sampling procedure is considered.

(i)
Samples of n items are randomly selected from the lot and are tested according to the above test procedure.
(ii)
Maximum likelihood estimators (MLEs) and , respectively, of location parameter μ and scale parameter σ at normal operating condition, respectively, of Burr type XII distribution are obtained from the test data.
(iii)
Schneider’s [9] approach to k-method is used wherein sample mean and standard deviation are replaced by MLEs of location parameter and scale parameter of log life distribution, respectively. In this paper k₁ instead of k has been used as acceptability constant. The value of test statistic is compared with L^′; the lot is accepted if T^′ ≥ L^′ and rejected otherwise. The sample size n and acceptability constant k₁ determined using variance optimality criterion subject to the constraints that the lots with fraction nonconforming are accepted with probability of at least and lots with are rejected with probability of at least .

6. Model Formulation

Maximum likelihood method has been used to estimate the model parameters α, c, and acceleration factors, A₁ and A₂, from the test data.

6.1. Likelihood Function

The likelihood function based on “n” observation is

()

where

()

The first-order partial derivatives of log-likelihood function of the ith unit with respect to A₁, A₂, α, and c are given by

()

On summing these partial derivatives and equating them to zero, likelihood equations are obtained. Since the closed form solutions of above likelihood equations are very hard to obtain, so further numerical treatment is required to obtain the MLEs of A₁, A₂, α, and c.

6.2. Fisher Information Matrix

The Fisher information matrix F(A₁, A₂, α, c) ≡ F is the 4 × 4 symmetric matrix of expectation of negative second-order partial derivatives of the log likelihood function with respect to A₁, A₂, α, and c. Consider

()

where the values of these elements are given in Appendix A.

6.3. Asymptotic Variance of Test Statistic T^′

For any plan, the asymptotic variance-covariance matrix of the MLEs

is the inverse of the corresponding Fisher information matrix; that is,

()

The asymptotic variance of the test statistic T^′ is given by

()

where V is obtained in Appendix B.

7. OC Curve

The operating characteristic (OC) curve measures the performance of a sampling plan and plots the probability of accepting the lot versus the proportion nonconforming of the lot. Based on the asymptotic distribution theory,

()

The standardized variate using (14) is

()

The OC curve is obtained by plotting the probability of accepting the lot, L_p, given as

()

against the fraction nonconforming, p, where u_p = (L^′ − μ)/σ is the quantile of the standard logistic distribution corresponding to the fraction nonconforming p, and Φ(·) is the standard normal distribution function. Therefore, the following equations have to be solved for

and n^* in order to obtain an optimal sampling plan for two given points

and

on the OC curve,

()

where

and

denote the quantiles of the standard normal distribution and

and

are the quantiles of the standard log-life distribution. Thus, on solving (18),

()

where

()

and V is given in (14).

See Schneider [9] for reference.

8. Formulation of an Optimization Problem

V in (14) is a function of A₁, A₂, η, α, c, and k. Thus, the optimal design problem can be formulated as a nonlinear optimization problem:

()

Since the sample size is unknown while minimizing V, therefore instead of giving minimum mean number of failures (MMNF) a prespecified value in advance, 0.1, is assigned to the ratio of MMNF and the sample size at each stress level. Another suitable number for MMNF can be specified according to cost, time, and precision implications (see Yang [2]). The optimum values of ϕ_i, i = 1,2, 3, are found by minimizing V under type I censoring, using NMinimize option of Mathematica 8.

9. A Numerical Example

In this section, a hypothetical constant-stress PALTSP experiment is considered to illustrate the methods described in this paper.

9.1. OC Curve

Choose two points and on the OC curve as (0.01, 0.99) and (0.10, 0.10), respectively.

9.2. Optimal Lot Acceptability Constant

Compute the acceptability constant k₁, using (19).

Since , , , and , we have k₁ = ((1.28155(−5.98519))−((−3.62346)(−2.32635)))/((−2.32635)−(1.28155)) = 4.46236.

9.3. Optimal Plan

Optimal

, i = 1,2, 3, and n^* are using (22). These are given in Table 1 using the following hypothetical data set:

()

Table 1 shows that optimal sample size decreases as A₁ increases and optimal sample proportions allocated to accelerated condition A₂ increase as A₁ increases.

Table 1. Change in

, i = 1,2, 3 for different values of A₁ (A₂ = 3, η = 5, α = 0.9, c = 3.5, and k = 4).

A₁				n^*
1.5	0.29387	0.33916	0.36697	37.2889 ≈ 37
1.6	0.23162	0.23576	0.53262	36.6683 ≈ 37
1.7	0.19098	0.21097	0.59805	35.8638 ≈ 36
1.8	0.1584	0.20729	0.63431	35.1254 ≈ 35
1.9	0.13196	0.21318	0.65486	34.5078 ≈ 35
2	0.11085	0.22402	0.66513	34.0173 ≈ 34

9.4. Optimal Acceptance Sampling Plan

Let us consider the lower specification limit of L as L^′ (ln⁡⁡L) indicating that items with lifetime shorter than ln⁡⁡L are nonconforming. For given lower specification limit L^′, lot is accepted if , lot is accepted and otherwise rejected.

Figure 1 depicts the OC curve obtained from u_P, V, n^* and the two points and .

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

OC curve with as (0.01, 0.99) and as (0.10, 0.10).

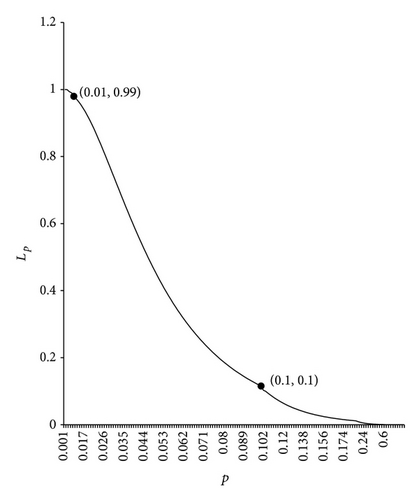
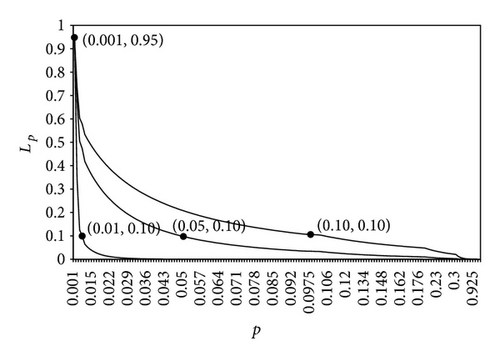
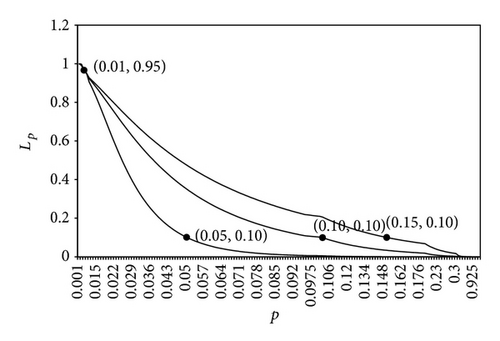
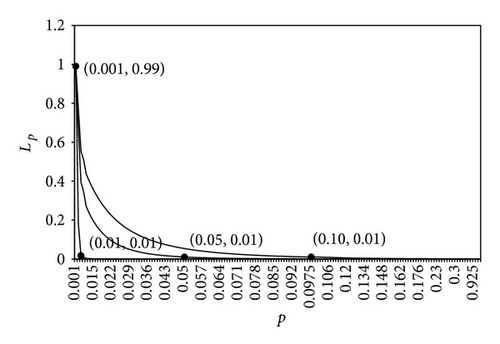
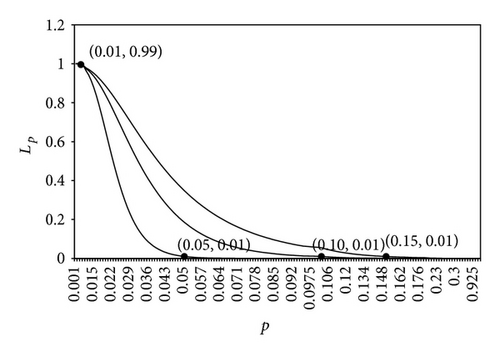
Tables 2 and 3 present optimum sampling plan for various values of and when ( and (0.99, 0.01). It is observed that for given as increases optimal “n^*” decreases, optimal increases, and optimal and optimal decrease. Using the data in Table 2, Figures 2 and 3 depict the OC curve obtained from the two points as (0.001, 0.95), (0.01, 0.95) and as (0.01, 0.10), (0.05, 0.10), (0.10, 0.10); (0.05, 0.10), (0.01, 0.10), (0.15, 0.10), respectively. In a similar manner, data in Table 3 has been used in plotting OC curve in Figures 4 and 5 by taking as 0.99 and as 0.01.

Table 2. Effects of various values of

and

on optimal ALT plans (A₁ = 1.5, A₂ = 3, η = 5, α = 0.9, c = 3.5, and k = 4).

,
		k₁	k₂	V*				n^*
0.001	0.01	6.99603	1.60734	3.27656	0.16048	0.40322	0.43630	65
	0.05	6.07697	0.55073	2.45800	0.19573	0.38629	0.41798	17
	0.1	5.66856	0.39268	2.13194	0.21515	0.37697	0.40789	10

0.01	0.05	5.06613	3.20311	1.69332	0.24966	0.36039	0.38995	66
	0.1	4.65773	1.53536	1.42466	0.27827	0.34665	0.37508	27
	0.15	4.41008	1.09052	1.27305	0.29829	0.33703	0.36468	17

Table 3. Effects of various values of

and

on optimal ALT plans (A₁ = 1.5, A₂ = 3, η = 5, α = 0.9, c = 3.5, and k = 4).

,
		k₁	k₂	V*				n^*
0.001	0.01	7.13931	4.06301	3.41476	0.15582	0.40546	0.43872	170
	0.05	6.32175	1.39212	2.66454	0.18532	0.39129	0.42339	45
	0.1	5.95844	0.99262	1.47615	0.27219	0.34957	0.37824	18

0.01	0.05	5.16763	8.09678	1.76368	0.24326	0.36346	0.39328	175
	0.1	4.80432	3.88106	1.51843	0.26743	0.35186	0.38072	72
	0.15	4.58403	2.75661	1.37865	0.28400	0.34390	0.37211	47

10. Sensitivity Analysis

To formulate an optimum sampling plan, the information about acceleration factors A₁ and parameters of the model α and c is needed as incorrect choice of these results in poor estimates of the parameters. The effects of incorrect preestimates of A₁, A₂, α, and c in terms of the relative increase in asymptotic variance of test statistic have been studied. The percentage deviations (PD) of the resulting optimal settings are measured by PD = (|V^** − V^* | /V^*) × 100, where V^* is the setting obtained with the given design parameters, and V^** is the one obtained when the parameter is misspecified. Tables 4 and 5 show that irrespective of whether the incorrect variance is smaller or larger than the true variance, the proposed optimum plan is robust since the percentage deviation in variance is small.

Table 4. Effects of incorrect preestimate “α” on optimal ALT plans (A₁ = 1.5, A₂ = 3, η = 5, α = 0.9, c = 3.5, and k = 4, V^* = 1.30435).

% change	Incorrect sample proportions				Incorrect variance	% deviation
% change	α				V**	PD
1%	0.909	0.36852	0.50889	0.12260	1.29050	1.06182
−1%	0.918	0.25565	0.28443	0.45992	1.30919	0.37156
2%	0.927	0.37624	0.52376	0.10000	1.26266	3.19600
−2%	0.936	0.22676	0.25874	0.51449	1.31231	0.61030
3%	0.945	0.37750	0.52250	0.10000	1.23615	5.22824
−3%	0.891	0.20252	0.24549	0.55199	1.31570	0.87059

Table 5. Effects of incorrect preestimate “c” on optimal ALT plans (A₁ = 1.5, A₂ = 3, η = 5, α = 0.9, c = 3.5, and k = 4, V^* = 1.30435).

% change	Incorrect sample proportions				Incorrect variance	% deviation
% change	c				V**	PD
1%	3.535	0.23483	0.26473	0.50044	1.28556	1.44015
−1%	3.570	0.37585	0.52415	0.10000	1.29585	0.65107
2%	3.605	0.19437	0.24250	0.56313	1.26608	2.93382
−2%	3.640	0.37800	0.52200	0.10000	1.27416	2.31434
3%	3.675	0.16283	0.23735	0.59982	1.25043	4.13323
−3%	3.465	0.37927	0.52073	0.10000	1.25527	3.76273

11. Conclusion

In this paper we have formulated an optimum time-censored constant-stress PALTSP for the Burr type XII life distribution using hazard acceleration. Single sampling plan by variables has been used. The acceptance/rejection decision of the lot involves k-method in which Schneider’s [9] approach has been used with sample mean replaced by MLE of location parameter and standard deviation replaced by MLE of scale parameter of the log-lifetime distribution with lower specification limit specified. The optimum plan consists in finding optimum allocation at normal operating condition and accelerated conditions by minimizing the variance of the test statistic meant for deciding on lot acceptability. The sensitivity analysis has been carried out and it has been found that if the misspecified values of the parameters are not too far from the true values, the optimum plan is robust.

Acronyms

ALT:: Accelerated life test
ALTSP:: Accelerated life test sampling plan
PALT:: Partially accelerated life test
PALTSP:: Partially accelerated life test sampling plan
Asvar:: Asymptotic variance
Ascov:: Asymptotic covariance
cdf:: Cumulative distribution function
pdf:: Probability density function
MLE:: Maximum likelihood estimate.

Notations

A₁, A₂:: Acceleration factors (A₂ > A₁ > 1)
:: , i = 1,2
ϕ₁, ϕ₂, ϕ₃:: Proportion of sample allocated to normal operating condition, accelerated condition , and accelerated condition , respectively, where
:: Optimum proportion of sample allocated to normal operating condition, accelerated condition A₁, and accelerated condition A₂, respectively, where
n:: Total number of test items in a PALTSP
nϕ_i:: Items allocated to normal operating condition, accelerated condition A₁, and accelerated condition A₂, respectively, i = 1,2, 3
:: Number of items failed at normal operating condition, accelerated condition A₁, and accelerated condition , respectively
:: Number of censored items at normal operating condition, accelerated condition A₁, and accelerated condition A₂, respectively
Y, X₁ & X₂:: Lifetime of an item at normal operating condition, accelerated condition A₁, and accelerated condition A₂, respectively
T:: ln⁡⁡Y
t_i:: Observed log-lifetime of ith item tested at normal operating condition
t_1j:: Observed log-lifetime of jth item tested at accelerated condition A₁
t_2j:: Observed log-lifetime of jth item tested at accelerated condition A₂
η:: Censoring time
η^′:: Log-censoring time
α:: Scale parameter (α > 0)
c, k:: Shape parameter (c > 0, k > 0)
F(·):: Cumulative distribution function
f₁(·):: Probability density function at normal operating condition
R₁(·):: Reliability function at normal operating condition
h₁(·):: Hazard (failure) rate at normal operating condition
f_i(·):: Probability density function at accelerated conditions A_i, i = 1,2
R_i(·):: Reliability function at accelerated conditions A_i, i = 1,2
h_i(·):: Hazard (failure) rate at accelerated conditions A_i, i = 1,2
∧:: A maximum likelihood estimate
:: Indicator functions: ; and .
:: Ordered log-lifetimes times at normal operating condition
:: Ordered log-lifetimes at accelerated condition A₁
:: Ordered log-lifetimes at accelerated condition A₂.

Conflict of Interests

The authors declare that there is no conflict of interests regarding the publication of this paper.

Acknowledgments

The authors are grateful to the referees for their valuable comments. This research work is supported by R&D Grant received from the University of Delhi, Delhi, India.

Appendices

A.

The elements of Fisher Information matrix are

()

B.

Using delta method, V in (20) has been obtained.

Let

()

where

is a transpose of

and

()

Further, let

()

where

is a transpose of

and

()

Then,

()

References

1 Nelson W., Accelerated Testing—Statistical Models, Test Plans, and Data Analyses, 1990, John Wiley & Sons, New York, NY, USA.
10.1002/9780470316795
Google Scholar
2 Yang G.-B., Optimum constant-stress accelerated life-test plans, IEEE Transactions on Reliability. (1994) 43, no. 4, 575–581, 2-s2.0-0028730662, https://doi.org/10.1109/24.370223.
10.1109/24.370223
Web of Science® Google Scholar
3 DeGroot M. H. and Goel P. K., Bayesian estimation and optimal designs in partially accelerated life testing, Naval Research Logistics Quarterly. (1979) 26, 223–2235.
10.1002/nav.3800260204
Web of Science® Google Scholar
4 Bai D. S., Chung S. W., and Chun Y. R., Optimal design of partially accelerated life tests for the lognormal distribution under type I censoring, Reliability Engineering and System Safety. (1993) 40, no. 1, 85–92, 2-s2.0-0027255626.
10.1016/0951-8320(93)90122-F
Web of Science® Google Scholar
5 Ismail A., The test design and parameter estimation of pareto lifetime distribution under partially accelerated life tests [Ph.D. thesis], 2004, Department of Statistics, Faculty of Economics & Political Science, Cairo University, Cairo, Egypt.
Google Scholar
6 Bhattacharyya G. K. and Soejoeti Z., A tampered failure rate model for step-stress accelerated life test, Communication in Statistics—Theory and Methods. (1989) 18, 1627–11643.
10.1080/03610928908829990
Web of Science® Google Scholar
7 Bai D. S. and Chung S. W., Optimal design of partially accelerated life tests for the exponential distribution under type-I censoring, IEEE Transactions on Reliability. (1992) 41, no. 3, 400–406, 2-s2.0-0026927871, https://doi.org/10.1109/24.159807.
10.1109/24.159807
Web of Science® Google Scholar
8 Abdel-Hamid A. H., Constant-partially accelerated life tests for Burr type-XII distribution with progressive type-II censoring, Computational Statistics & Data Analysis. (2009) 53, no. 7, 2511–2523, 2-s2.0-61849167473, https://doi.org/10.1016/j.csda.2009.01.018.
10.1016/j.csda.2009.01.018
Web of Science® Google Scholar
9 Schneider H., Failure-censored variables-sampling plans for lognormal and Weibull distributions, Technometrics. (1989) 31, no. 2, 199–206, 2-s2.0-0024656381.
10.1080/00401706.1989.10488513
Web of Science® Google Scholar

Citing Literature

All articles

Optimum Time-Censored Constant-Stress PALTSP for the Burr Type XII Distribution Using Tampered Failure Rate Model

Abstract

1. Introduction