This paper investigates the oscillatory behavior of the solutions for a three-node neural network with discrete and distributed delays. Two theorems are provided to determine the conditions for oscillating solutions of the model. The criteria for selecting the parameters in this network are derived. Some simulation examples are presented to illustrate the effectiveness of the results.

1. Introduction

Neural networks are complex and large-scale dynamical systems. Time delay is inevitably encountered in implementation of dynamical neural networks and is frequently a source of oscillation and instability. On the one hand, information transmission from one neuron to another neuron may make the response of networks with discrete delays. On the other hand, neural networks usually have spatial extent due to the presence of a multitude of parallel pathways with a variety of axon sizes and lengths. Thus, the distributed delays in neural system need to be considered. In the past two decades, many researches have studied various neural networks with discrete and distributed delays [1–4]. In [1], Gopalsamy and Leung studied the following neural network model:

(1)

By means of the Lyapunov functional, the authors obtained some necessary and sufficient conditions for the existence of a globally asymptotically stable equilibrium point of system (1). Ruan and Filfil [2] considered a two-neuron network model with multiple discrete and distributed delays as follows:

(2)

where the delayed feedback kernel satisfies

and

,2). Local stability analyses are carried out for model (2). Computer simulations are performed to illustrate the obtained results. Liao et al. [3] discussed a two-neuron system with distributed delays in the frequency domain as follows:

(3)

where F(r) is a strong kernel. For simplicity, the authors set c₁ = c₂ = 0. Let

(4)

Then system (3) is equivalent to the following model:

(5)

By applying the frequency domain approach and analyzing the characteristic equation, the Hopf bifurcation occurs when the mean delay μ exceeds a critical value. Thus, there is a family of periodic solutions bifurcates from the equilibrium point. Recently, Hajihosseini et al. [4] have investigated the following three-node network model:

(6)

where w₁ and w₂ are parameters. The authors also make the change of variables

such that system (6) changes to the following:

(7)

Under the restrictive condition |w₁ + w₂ | < 1, the Hopf bifurcation and stability of the bifurcating periodic solutions have been discussed. There are many authors who have studied the bifurcating periodic solutions for various models [5–14]. It is well known that the basic method in studying the bifurcating periodic solution for a time delay system is to discuss an algebraic equation in which the bifurcating value will be determined. Motivated by the above models we shall concern the existence of oscillating solutions for the following three-node network system with discrete and distributed delays:

(8)

where F(r) = μ²re^−μr (μ > 0) is a strong kernel function, the passive decay rates a₁, a₂, and a₃ are positive constants, b_i, c_i, and l_i (i = 1,2,3) are constants, and delays τ₁, τ₂, and τ₃ are nonnegative constants. It was emphasized that bifurcating approach is hard to deal with model (8), because it is very difficult to find the bifurcating parameter when τ₁, τ₂, and τ₃ are different nonnegative constants. In order to discuss the existence of oscillating solutions for system (8) we adopt Chafee’s criterion [15]. A time delay system will generate a limit cycle if the system has a unique unstable equilibrium point and bounded solutions. In other words, there exists an oscillatory solution of the model. System (8) can accord with the demands of Chafee’s criterion; we refer the reader to [16, appendix].

2. Preliminaries

First we assume that the activation functions f and g both are monotone continuous bounded functions. f, g ∈ C⁴(R), f(0) = g(0) = 0, uf(u) > 0, and ug(u) > 0 for u ≠ 0. For example, f(u) = tanh(u), and g(u) = arctan⁡ (u) satisfy those conditions. For the kernel function F(r) = μ²re^−μr (μ > 0) we have

(9)

From (9) we get

(10)

Taking the derivative on both sides of system (8) we obtain

(11)

Set

(12)

so (11) can be rewritten as follows:

(13)

Taking the derivative again on both sides of (13) and using (10) give

(14)

Now by setting x₄(t) = dx₁(t)/dt, x₅(t) = dx₂(t)/dt, x₆(t) = dx₃(t)/dt,

, and

, we get the following time delay equivalent system of (8):

(15)

The linearization of system (15) around the zero point is the following:

(16)

System (16) can be written as a matrix form:

(17)

where

= (x₁(t − τ₁), x₂(t − τ₂), x₃(t − τ₃), x₄(t − τ₁), x₅(t − τ₂), x₆(t − τ₃), x₇(t − τ₁), x₈(t − τ₂), and x₉(t − τ₃)) ^T. So,

(18)

where p₇₁ = −μ²a₁, p₇₃ = c₃μ²g^′(0), p₇₄ = −(2μa₁ + μ²), p₇₇ = −(a₁ + 2μ), p₈₁ = c₁μ²g^′(0), p₈₂ = −μ²a₂, p₈₅ = −(2μa₂ + μ²), p₈₈ = −(a₂ + 2μ), p₉₂ = c₂μ²g^′(0), p₉₃ = −μ²a₃, p₉₆ = −(2μa₃ + μ²), p₉₉ = −(a₃ + 2μ); q₇₂ = μ²b₂f^′(0), q₇₅ = −2μb₂f^′(0), q₇₈ = b₂f^′(0), q₈₃ = μ²b₃f^′(0), q₈₆ = −2μb₃f^′(0), q₈₉ = b₃f^′(0), q₉₁ = μ²b₁f^′(0), q₉₄ = −2μb₁f^′(0), and q₉₇ = b₁f^′(0).

Lemma 1. All solutions of system (8) are bounded.

Proof. Since we assume that f and g both are monotone continuous bounded functions. So we have |f(u) | ≤ M and |g(u) | ≤ N (M and N are positive constants). From (8) we obtain

(19)

where A₁ = |b₂|M + |c₃|N, A₂ = |b₃|M + |c₁|N, and A₃ = |b₁|M + |c₂|N. Thus, |x_i(t)| ≤ (A_i/a_i)+|x_i(0)| (i = 1, 2, 3). This means that the solutions of system (8) are uniformly bounded.

Lemma 2. Assume that the matrix

(20)

is a nonsingular matrix. Then system (8) has a unique equilibrium point.

Proof. Noting that f and g both are monotone continuous bounded functions satisfying f(0) = g(0) = 0. Then f(x) = f^′(0)x + α, g(x) = g^′(0)x + β, where α and β both are higher order infinitesimals when x → 0. From (8), an equilibrium point is a solution of the following algebraic equation:

(21)

Noting that , then we have

(22)

If is another equilibrium point of system (8), neglecting of the higher order infinitesimal, we obtain

(23)

The matrix form of (23) is follows:

(24)

Since B is a nonsingular matrix based on the algebraic knowledge one can have x^* − y^* = 0 or x^* = y^*. This means that system (8) has a unique equilibrium point. Obviously, the unique equilibrium point exactly is zero point since f(0) = g(0) = 0.

3. Oscillating Solutions Analysis

We adopt the following norms of vectors and matrices: , . The measure σ(P) of the matrix P is defined by , which for the chosen norms reduces to .

In order to discuss the instability of equilibrium point for system (8), we consider the equivalent system (15) of (8). Note that the linearized system of (15) is (16). Obviously, if the trivial solution of (16) is unstable, it implies that the trivial solution of system (15) is unstable and thus the instability of the trivial solution of system (8). Therefore, we first have

Theorem 3. Assume that system (8) has a unique equilibrium point and the determinant of matrix P is not equal to zero. Let ρ₁, ρ₂, …, ρ₉, ϱ₁, ϱ₂, …, ϱ₉ be the eigenvalues of the matrixes P and Q, respectively. If there is at least one Reρ_i> 0 (Im⁡ρ_i may be equal to zero) or there exists one positive real eigenvalue ϱ_j>|ρ_j|, for some j ∈ {1,2, …, 9}, then the unique equilibrium point, namely, the trivial solution of system (16) is unstable, implying that the equivalent system (15) or (8) generates oscillating solutions.

Proof. Since Q is a singular matrix, set ϱ₁ = ϱ₂ = ⋯ = ϱ₆ = 0. For given value of μ, let ρ₁, ρ₂, …, ρ₉ be the eigenvalues of the matrix P. Thus, the characteristic equation of system (16) is as follows:

(25)

where

(26)

(27)

Since there is at least one Reρ_i > 0, without loss of generality, set Reρ₁ > 0. From ϱ₁ = 0 we have the equation λ − ρ₁ = 0. This means that λ = ρ₁, and there is a Re λ > 0. So, the unique equilibrium point of system (16) is unstable based on the theory of differential equation. If by corresponding some ρ_j we have ϱ_j>|ρ_j| j ∈ {1,2, …, 9}, we pointed out that there exists positive real root for transcendental equation . Let . Then f(λ) is a continuous function of λ. Since f(0) = −ρ_j − ϱ_j, from ϱ_j>|ρ_j|, we know that f(0) < 0. Obviously, there is a suitable large λ^* > 0 such that since can be suitably small. Thus, by the continuity of f(λ), there is a point, say such that . In other words, there is a positive real eigenvalue. In this case the unique equilibrium point of system (16) is also unstable. Since all solutions of the system are bounded, on the basis of Chafee’s criterion [15], system (15) generates a limit cycle, implying that there exists an oscillating solution of system (15) and therefore system (8).

Theorem 4. Assume that system (8) has a unique equilibrium point and the following inequalities hold:

(28)

where τ = min⁡⁡{τ₁, τ₂, τ₃} and τ^* = max⁡{τ₁, τ₂, τ₃}. Then the unique equilibrium point, namely, the trivial solution of system (16) is unstable, implying that the equivalent system (15) or (8) generates oscillating solutions.

Proof. First we consider system (16) in the case τ₁ = τ₂ = τ₃ = τ and we easily get:

(29)

Let ; then for some t^*, y(t) > 0 (t ≥ t^*) and we have

(30)

Consider the scalar equation

(31)

with y(s) = z(s) and s ∈ [t^*, t^* + τ]. According to the comparison theorem of differential equation, one can obtain

(32)

We claim that the trivial solution of (31) is unstable. Suppose that this is not true; then the characteristic equation associated with (31) given by

(33)

will have a real negative root say λ^* such that

, where

So we get

(34)

Thus

(35)

Based on the formula e^x ≥ ex (x > 0), from (35), we have

(36)

Inequality (36) contradicts the first inequality of (28). Therefore, our claim regarding the instability of the trivial solution is valid. Similarly, consider system (16) in the case τ₁ = τ₂ = τ₃ = τ^*; we know that the trivial solution is unstable if the second inequality of (28) holds. Note that τ ≤ τ_i ≤ τ^* (i = 1, 2, 3). So, the trivial solution of (16) is unstable when condition (28) holds, implying that the trivial solution of (15) is unstable. According to Chafee’s criterion, system (15) generates a limit cycle, suggesting that there is an oscillating solution of system (15) and therefore system (8).

4. Computer Simulations

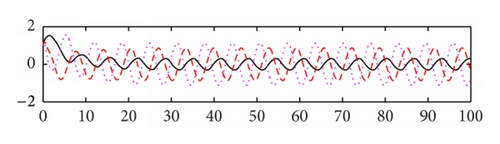
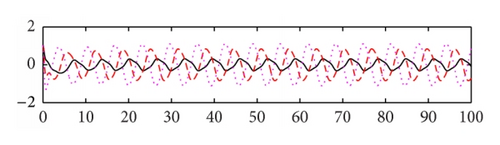
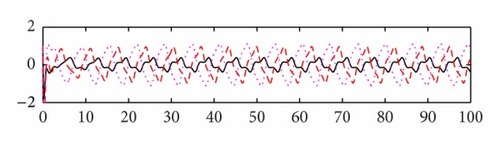
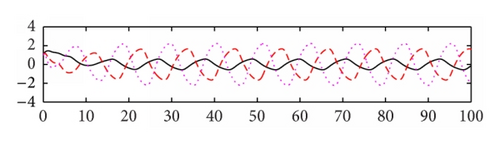
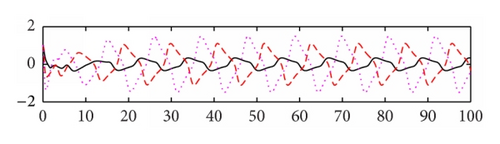
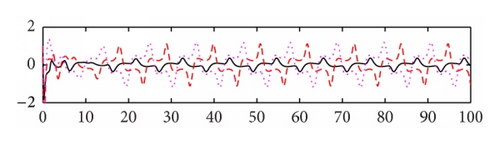
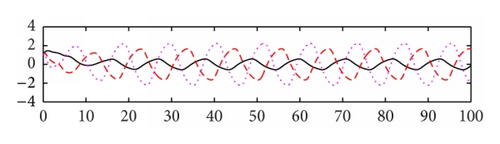
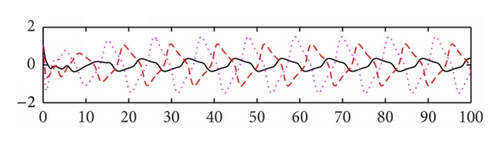
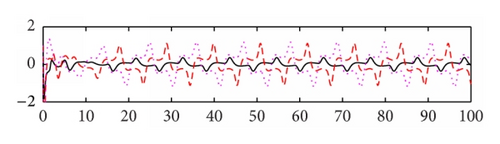
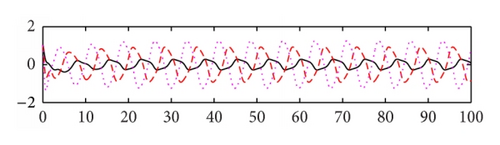
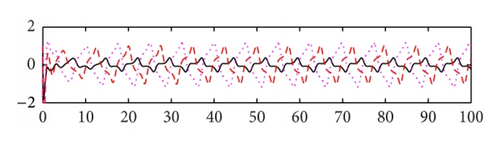
We use the equivalent system (15) of (8) for computer simulation. In Figure 1 both activation functions f(u) and g(u) are taken tanh (u). Thus, , f^′′(u) = g^′′(u) = 2(tanh⁡(u))³ − 2tanh⁡(u), and f^′(0) = g^′(0) = 1. We select μ = 5.5, a₁ = 0.48, a₂ = 0.65, a₃ = 0.78, b₁ = 0.6, b₂ = 0.8, b₃ = 0.9, c₁ = −0.8, and c₂ = −1.8, c₃ = 0.4. Then the eigenvalues of matrix P are −5.8250 ± 1.8620i, −1.7568 ± 2.5151i, −0.0000, −0.4840, −5.3568, −5.6392, and −8.2087 and the eigenvalues of matrix Q are −0.3780 ± 0.6547i, 0.7560, and 0, 0, 0, 0, 0, 0. Note that the eigenvalue 0.7560 of matrix Q is larger than |−0.4840| = 0.4840. Based on Theorem 3, the trivial solution of system (15) is unstable. The system generates an oscillating solution. In order to compare the effect of the time delays, we change the delays from (0.2, 0.3, and 0.4) to (1, 1.5, and 2), while keeping the other parameters as shown in Figure 1. We see that the oscillatory amplitude and frequency both are changed (see Figure 2). In Figure 3, we keep the parameter values the same as Figure 2, the activation function g(u) = tanh⁡(u), and change the activation function f(u) = arctan⁡(u). Then f^′(u) = 1/(1 + u²) and . We see that the graph is changed slightly in comparison with Figure 2. In Figure 4, we set the activation function f(u) = 1/(1 + e^−2u) and g(u) = (e^−2u − 1)/(1 + e^−2u). Then , , , and . Thus f^′(0) = 1/2 and g^′(0) = −1. Note that f(0) = 1/2 ≠ 0 and g(0) = −1/2 ≠ 0. When we select the parameters as follows: μ = 3.5, a₁ = 0.18, a₂ = 0.15, a₃ = 0.19, b₁ = 0.05, b₂ = 0.08, b₃ = 0.12, c₁ = −0.6, and c₂ = 0.8, c₃ = 0.5, time delays are (0.5, 0.6, and 0.7). The oscillatory solutions also appeared. This means that the restrictive condition f(0) = g(0) = 0, uf(u) > 0, and ug(u) > 0 for u ≠ 0 is only for convenience of the proof.

Details are in the caption following the image — **Figure 1 (a) solid line: x1(t), dashed line: x2(t), and dotted line: x3(t)**
Open in figure viewer PowerPoint

Oscillatory behavior of the solutions: mu = 3.5, delays: (0.5, 0.6, and 0.7), and activation functions: f(u) = g(u) = tanh(u).

5. Conclusion

This paper discusses the oscillatory behavior of the solutions for a three-node network model with discrete and distributed delays. Two theorems are provided to ensure the existence of oscillating solutions for the model. Computer simulations suggested that our theorems are only sufficient conditions. How to find a necessary condition is still an open problem.

Conflict of Interests

The author declares that there is no conflict of interests regarding the publication of this paper.

Acknowledgment

This work is supported by Grant no. 11361010 from NNFS of China to Chunhua Feng.

References

1 Gopalsamy K. and Leung I. K. C., Convergence under dynamical thresholds with delays, IEEE Transactions on Neural Networks. (1997) 8, no. 2, 341–348, 2-s2.0-0031101884, https://doi.org/10.1109/72.557672.
Google Scholar
2 Ruan S. and Filfil R. S., Dynamics of a two-neuron system with discrete and distributed delays, Physica D. (2004) 191, no. 3-4, 323–342, 2-s2.0-1842635257, https://doi.org/10.1016/j.physd.2003.12.004.
Google Scholar
3 Liao X., Li S., and Chen G., Bifurcation analysis on a two-neuron system with distributed delays in the frequency domain, Neural Networks. (2004) 17, no. 4, 545–561, 2-s2.0-1942454843, https://doi.org/10.1016/j.neunet.2003.10.001.
Google Scholar
4 Hajihosseini A., Lamooki G. R., Beheshti B., and Maleki F., The Hopf bifurcation analysis on a time-delayed recurrent neural network in the frequency domain, Neurocomputing. (2010) 73, 991–1005, 2-s2.0-75749127369, https://doi.org/10.1016/j.neucom.2009.08.018.
Google Scholar
5 Cai T. Y., Zhang H. G., and Yang F. H., Simplified frequency method for stability and bifurcation of delayed neural networks in ring structure, Neurocomputing. (2013) 121, 416–422.
Google Scholar
6 Sebdani R. M. and Farjami S., Bifurcations and chaos in a discrete-time-delayed Hopfield neural network with ring structures and different internal delays, Neurocomputing. (2013) 99, 154–162.
Google Scholar
7 Huang C., Huang L., Feng J., Nai M., and He Y., Hopf bifurcation analysis for a two-neuron network with four delays, Chaos, Solitons and Fractals. (2007) 34, no. 3, 795–812, 2-s2.0-34247122734, https://doi.org/10.1016/j.chaos.2006.03.089.
Google Scholar
8 Ding Y. T., Jiang W. H., and Yu P., Bifurcation analysis in a recurrent neural network model with delays, Communications in Nonlinear Science and Numerical Simulation. (2013) 18, 351–372.
Google Scholar
9 Guo S., Chen Y., and Wu J., Two-parameter bifurcations in a network of two neurons with multiple delays, Journal of Differential Equations. (2008) 244, no. 2, 444–486, 2-s2.0-36849021007, https://doi.org/10.1016/j.jde.2007.09.008.
Google Scholar
10 Huang Y. and Yang X., Hyperchaos and bifurcation in a new class of four-dimensional Hopfield neural networks, Neurocomputing. (2006) 69, no. 13-15, 1787–1795, 2-s2.0-33745194156, https://doi.org/10.1016/j.neucom.2005.11.001.
Web of Science® Google Scholar
11 Sun C., Han M., and Pang X., Global Hopf bifurcation analysis on a BAM neural network with delays, Physics Letters A. (2007) 360, no. 6, 689–695, 2-s2.0-33751241112, https://doi.org/10.1016/j.physleta.2006.08.078.
Google Scholar
12 Zhao H., Wang L., and Ma C., Hopf bifurcation and stability analysis on discrete-time Hopfield neural network with delay, Nonlinear Analysis: Real World Applications. (2008) 9, no. 1, 103–113, 2-s2.0-35248841074, https://doi.org/10.1016/j.nonrwa.2006.09.005.
Web of Science® Google Scholar
13 Ncube I., Stability switching and Hopf bifurcation in a multiple-delayed neural network with distributed delay, Journal of Mathematical Analysis and Applications. (2013) 407, 141–146.
Google Scholar
14 Dong T. and Liao X. F., Hopf-Pitchfork bifurcation in a simplified BAM neural network model with multiple delays, Journal of Computational and Applied Mathematics. (2013) 253, 222–234.
Google Scholar
15 Chafee N., A bifurcation problem for a functional differential equation of finitely retarded type, Journal of Mathematical Analysis and Applications. (1971) 35, no. 2, 312–348, 2-s2.0-0000291028.
Google Scholar
16 Feng C. and Plamondon R., An oscillatory criterion for a time delayed neural ring network model, Neural Networks. (2012) 29-30, 70–79, 2-s2.0-84860345037, https://doi.org/10.1016/j.neunet.2012.01.008.
PubMed Web of Science® Google Scholar

All articles

Oscillatory Behavior on a Three-Node Neural Network Model with Discrete and Distributed Delays

Abstract

1. Introduction

2. Preliminaries

3. Oscillating Solutions Analysis

4. Computer Simulations

5. Conclusion

Conflict of Interests

Acknowledgment

References

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Oscillatory Behavior on a Three-Node Neural Network Model with Discrete and Distributed Delays

Abstract

1. Introduction

2. Preliminaries

3. Oscillating Solutions Analysis

4. Computer Simulations

5. Conclusion

Conflict of Interests

Acknowledgment

References

Figures

References

Related

Information