Volume 2014, Issue 1 532453

Research Article

Open Access

Mathematical Modeling of the Expert System Predicting the Severity of Acute Pancreatitis

Corresponding Author

Maria A. Ivanchuk

[email protected]

Department of Biological Physics and Medical Informatics, Bukovinian State Medical University, Kobyljanska Street 42, Chernivtsi 58000, Ukraine bsmu.edu.ua

Search for more papers by this author

Vitalij V. Maksimyuk,

Vitalij V. Maksimyuk

Department of Surgery, Bukovinian State Medical University, Golovna Street 137, Chernivtsi 58000, Ukraine bsmu.edu.ua

Search for more papers by this author

Igor V. Malyk,

Igor V. Malyk

Department of the System Analysis and Insurance and Financial Mathematics, Chernivtsi National University of Yuriy Fedkovich, Unversitetska Street 12, Chernivtsi 58012, Ukraine chnu.edu.ua

Search for more papers by this author

Maria A. Ivanchuk,

Corresponding Author

Maria A. Ivanchuk

[email protected]

Department of Biological Physics and Medical Informatics, Bukovinian State Medical University, Kobyljanska Street 42, Chernivtsi 58000, Ukraine bsmu.edu.ua

Search for more papers by this author

Vitalij V. Maksimyuk,

Vitalij V. Maksimyuk

Department of Surgery, Bukovinian State Medical University, Golovna Street 137, Chernivtsi 58000, Ukraine bsmu.edu.ua

Search for more papers by this author

Igor V. Malyk,

Igor V. Malyk

Department of the System Analysis and Insurance and Financial Mathematics, Chernivtsi National University of Yuriy Fedkovich, Unversitetska Street 12, Chernivtsi 58012, Ukraine chnu.edu.ua

Search for more papers by this author

First published: 09 June 2014

https://doi.org/10.1155/2014/532453

Academic Editor: Daniel Kendoff

Share a link

Email
Wechat
Bluesky

Abstract

The method of building the hyperplane which separates the convex hulls in the Euclidean space Rⁿ is proposed. The algorithm of prediction of the presence of severity in patients based on this method is developed and applied in practice to predict the presence of severity in patients with acute pancreatitis.

1. Introduction

During the last decades, pronounced tendency to the relentless increase in morbidity in acute pancreatitis is observed. Thus, the depth of pathomorphological pancreatic parenchyma lesions can vary from the development of edematous pancreatitis up to pancreatic necrosis. However, accurate predicting of the probable nature of the lesion of the pancreas in the early stages of acute pancreatitis is one of the most difficult problems of modern pancreatology. Diagnostic and the predictive probability of existing laboratory and instrumental diagnostic markers and rating scales does not exceed 70–80% [1–3]. Such situation is a major difficulty in selecting the adequate treatment strategy in the initial stages of acute pancreatitis. Thus the search for new methods of accurate predicting of acute pancreatitis’ severity becomes an urgent problem.

Development of mathematical approaches for prediction in medicine was developed by Fisher, the father of the linear discriminant analysis [4]. Currently, there are many approaches to solving this problem: cluster analysis, the construction of predictive tables, image recognition, and linear programming. Fundamentals of building the prognostic tables and Wald serial analysis are described in [5]. Cluster analysis is commonly used for solving the tasks of medical prediction.

In the paper [6], the procedure of cluster analysis with a study of the indices of the daily variability of cardiac rhythm in patients with the ischemic disease of heart is examined. In [7] using national data from the Scientific Registry of Transplant Recipients authors compare transplant and wait-list hospitalization rates. They suggest two marginal methods to analyze such clustered recurrent event data; the first model postulates a common baseline event rate, while the second features cluster-specific baseline rates. Results from the proposed models to those based on a frailty model were compared with the various methods compared and contrasted. Three major considerations in designing a cluster analysis are described in [8]. The first relates to selection of the individuals. The second consideration is selection of variables for measurement and the third consideration is how many variables to choose to enter into a cluster analysis. To classify clinical phenotypes of anti-neutrophil cytoplasmic antibody-associated vasculitis, cluster analysis was used in [9]. Researches on the general theory of diagnosis, classification, and application of optimization methods for pattern recognition, solving applied problems in medicine and biology, are conducted by Mangasarian et al. for many years [10].

But universal method for solving problems of recognition, identification, and diagnosis does not exist. Therefore, development of methods for predicting in medicine still remains relevant. One among the many challenges of recognition is the task of constructing hyperplanes which separate two convex sets. Many manuscripts [11–16] are devoted to the solution of this problem.

We propose a methodology for constructing convex hulls and their separation, which can be used for modeling expert medical prognostic systems (e.g., to separate groups of patients with different degrees of severity of the disease for prediction of severity in patients).

2. Methods

2.1. Separation of the Convex Hulls

Let us have two sets of points

and

in Euclidean space Rⁿ. Let m be number of points in the set. We must find the separate hyperplane:

()

where 〈p, x〉 is the scalar product of the vectors p and x such that sets A and B can be placed in the different half-spaces:

()

To build the convex hull conv_A for the set A, for each of

points’ combinations from the set A, if it is possible, build the hyperplane

()

Coordinates of the vector p = (p¹, …, pⁿ) are found as minors (n − 1) order for elements of the first row of the matrix:

()

where x ∈ Rⁿ, a_i ∈ A,

. Coefficient β is determined from the following equation:

()

If all points of the set A are in the one of half-spaces of hyperplane H_P, then polygon a₁a₂ ⋯ a_n is one of the convex hull’s hyperfaces. The complex of all hyperfaces is the convex hull conv_A.

Point b_i ∈ B is called outlier if point b_i is internal for the conv_A. Point b_i is outlier if there is at least one hyperface a₁a₂ ⋯ a_n ∈ conv_A that

()

where point c ∈ int⁡ conv_A, point f is the intersection point of the hyperplane H_p (a₁a₂ ⋯ a_n ∈ H_p), and line

()

To find the point f let us write (3) in parametric form:

()

Put (8) in the hyperplane equation (3) and find parameter t:

()

To find coordinates of the point f let us put (9) in (8):

()

After finding all outliers from the sets A and B eject outliers from the set, with less number of outliers. Build the new convex hulls and find the outliers. If there are outliers in the new convex hulls, eject them. If there are not any outliers, the convex hulls do not intersect. According to consequence of Hahn-Banach theorem there is a nonzero linear functional L_p that separates conv_A and conv_B [17].

Find the separating functional L_p as hyperplane parallel to one of convex hulls’ hyperfaces. Choose hyperface so that convex hulls conv_A and conv_B are in different half-spaces formed by hyperplane parallel to this hyperface. Find points a_min⁡ ∈ conv_A and b_min⁡ ∈ conv_B so that . Let . For each hyperface and build the parallel hyperplane . If , for all a_i ∈ A, , and , for all b_j ∈ B, then L_p is separating hyperplane.

2.2. Modeling the Expert System of Predicting the Presence of Severity in Patients

Let us have two groups of patients: A, patients with severity, and B, patients without severity. There are n₀ parameters (factors which affect the severity) known for each patient.

During modelling we used the terms sensitivity (Se) and specificity (Sp):

()

where a is the true positives, b is the false positives (overdiagnosis errors), c is the false negatives (underdiagnosis errors), and d is the true negatives. The sensitivity of a clinical test refers to the ability of the test to correctly identify those patients with the disease. The specificity of a clinical test refers to the ability of the test to correctly identify those patients without the disease [18].

We created an algorithm of modelling the expert system in a way that uses the least amount of features for the best result. Information of the parameters was found using Kulback’s information measure [5]. We built convex hulls for the most informative factor. If convex hulls intersect, we found outliers—the points from the set A that are internal to conv_B and the points from the set B that are internal to conv_A. The set A outliers are underdiagnosis errors. The set B outliers are overdiagnosis errors. We built the prognostic system to find the patients with severity, so we rejected the outliers from the set B. Let the set be the set of outliers from B. After rejecting, we get a new set B^′ = B/O_B.

If you build the expert system for differential diagnosis, you reject outliers out of the set where there are less of them.

If the percentage of rejected points is more than the significance level

()

the next (the most informative) factor was added. The space dimension is increased by 1. In the new space convex hulls were built and the outliers were rejected. The space dimension was increased until preassigned significance level. If all available diagnostic information was used, but preassigned significance level was not reached, then decision of not sufficient information was taken. When preassigned significance level was reached, we found the separating hyperplanes. The algorithm for modelling the prognostic system is represented on the Figure 1. The results were checked in the control group and the hyperplane with maximal sensitivity was chosen.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Algorithm for modelling the prognostic system.

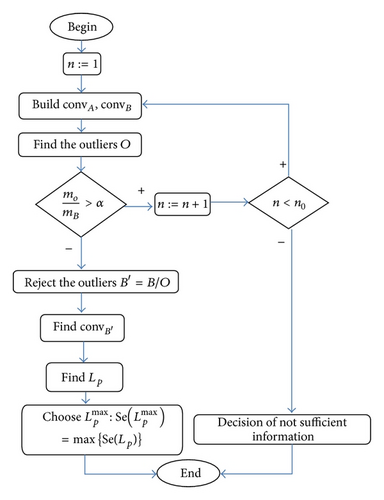
The complexity of this algorithm is O(mⁿ⁺¹) [19] if the convex hulls are built by search of all combinations of points. The complexity of this algorithm is O(m²) if the convex hulls are built by Jarvis march or “gift wrapping” algorithm [20].

3. Results

3.1. The Expert System of Predicting the Presence of Severity in Patients with Acute Pancreatitis

The research involved 60 persons with severe and 28 patients with nonsevere acute pancreatitis. Among them, there were 57 (64.8%) men and 31 (35.2%) women. The mean age was 48.54 years (±15.18) in males and 56.21 (±17.91) in females. The most common etiology was alcohol consumption (48.3%), followed by gallstones (34.2%). In 17.5% no identifiable cause was found.

The diagnostic criteria for acute pancreatitis were those defined by the 2006 AP Guidelines, as the presence of at least two of the following features: (1) characteristic abdominal pain, (2) elevation over 3 times the upper normal limit of serum amylase/lipase, and (3) characteristic features on computer tomography (CT) scan [21]. Severe acute pancreatitis was diagnosed according strictly to Atlanta criteria: Early Prognostic Scores, APACHE II ≥ 8, Ranson ≥ 3; Organ Failure, systolic pressure < 90 mmHg, creatinine > 2.0 mg/L after rehydration, PaO₂ ≤ 60 mmHg; Local Complications (on CT scan), Necrosis, Abscess, and Pseudocyst [22].

Patients were divided into two samples—training (50 patients with severity and 20 without them) and control (10 patients with severity and 8 without). The level of significance was α = 0,01. The algorithm presented above was used for patients with training set.

For n = 1, the percentage of outliers was 29.5%.
For n = 2, the percentage of outliers was 3%.
For n = 3, the percentage of outliers was 1.4%.
For n = 4, the percentage of outliers was 0%.

We got 8 hyperplanes which separate the convex hulls of the training samples. Two of them had higher sensitivity and specificity (we got only 1 (6%) of underdiagnosis errors and there were no overdiagnosis errors for the control sample with these hyperplanes):

()

where x¹ is time before hospitalization, x² is blood lipase, x³ is amylase urine, and x⁴ is BMI.

So, we built the expert system with sensitivity Se = 94%.

Statistical errors are seen only in 1 patient in the control group, who were diagnosed with interstitial edematous pancreatitis development on the background severe diabetes mellitus. According to Expert System the acute pancreatitis without severity was predicted. This error, in our view, is associated with late ambulation of the patient for medical care as a result of atypical course of acute pancreatitis, increased blood and urine amylase, and increased BMI, which is the characteristic signs of diabetes mellitus. That is, in this case, some of the most important prognostic parameters of acute pancreatitis have been characterized by different diseases in particular of diabetes mellitus, which caused the error.

4. Conclusions

The method of separation of convex hulls in Euclidean space by constructing a separating hyperplane parallel to one of the convex hulls hyperfaces is proposed. On the basis of this method the algorithm for modelling the prognostic system is stated. The proposed algorithm is applied in practice to predict the presence of severity in patients with acute pancreatitis and gives 94% correct results for the control sample, while diagnostic and the predictive probability of existing laboratory and instrumental diagnostic markers and rating scales does not exceed 70–80%. Clinical application of the developed mathematical model predicting the severity of acute pancreatitis promotes proper choice of treatment tactics and allows improving final results of these patients’ treatment.

Conflict of Interests

The authors declare that there is no conflict of interests regarding the publication of this paper.

References

1 Balthazar E. J., Acute pancreatitis: assessment of severity with clinical and CT evaluation, Radiology. (2002) 223, no. 3, 603–613, 2-s2.0-0036098977.
10.1148/radiol.2233010680
PubMed Web of Science® Google Scholar
2 Sathyanarayan G., Garg P. K., Prasad H. K., and Tandon R. K., Elevated level of interleukin-6 predicts organ failure and severe disease in patients with acute pancreatitis, Journal of Gastroenterology and Hepatology. (2007) 22, no. 4, 550–554, 2-s2.0-33947236241, https://doi.org/10.1111/j.1440-1746.2006.04752.x.
10.1111/j.1440-1746.2006.04752.x
CAS PubMed Web of Science® Google Scholar
3 Khanna A. K., Meher S., Prakash S. et al., Comparison of ranson, Glasgow, MOSS, SIRS, BISAP, APACHE-II, CTSI scores, IL-6, CRP, and procalcitonin in predicting severity, organ failure, pancreatic necrosis, and mortality in acute pancreatitis, HPB Surgery. (2013) 2013, 10, 367581, https://doi.org/10.1155/2013/367581.
10.1155/2013/367581
PubMed Google Scholar
4 Fisher R. A., Contributions To Mathematical Statistics, 1950, John Wiley & Sons.
Google Scholar
5 Gubler E. V. and Genkin A. A., Primenenie Neparametricheskih Kriteriev Statistiki v Medico-Biologicheskih Issledovanijah (Using the Nonparametric Statistic Criteria in Medical and Biological Researches), 1973, Leningrad, Russia.
Google Scholar
6 Borodulin A. I., Sviridov A. V., and Sudakov O. V., Using the cluster analysis in the in the diagnostic of ischemic heart disease, Prikladnie Informacionnie Aspekti Medicini. (2008) no. 2, 28–32.
Google Scholar
7 Schaubel D. E. and Cai J., Analysis of clustered recurrent event data with application to hospitalization rates among renal failure patients, Biostatistics. (2005) 6, no. 3, 404–419, 2-s2.0-26644475234, https://doi.org/10.1093/biostatistics/kxi018.
10.1093/biostatistics/kxi018
PubMed Web of Science® Google Scholar
8 Weatherall M., Shirtcliffe P., Travers J., and Beasley R., Use of cluster analysis to define COPD phenotypes, European Respiratory Journal. (2010) 36, no. 3, 472–474, 2-s2.0-77956601433, https://doi.org/10.1183/09031936.00035210.
10.1183/09031936.00035210
CAS PubMed Web of Science® Google Scholar
9 Mahr A., Katsahian S., Varet H. et al., Revisiting the classification of clinical phenotypes of anti-neutrophil cytoplasmic antibody-associated vasculitis: a cluster analysis, Annals of the Rheumatic Diseases. (2013) 72, no. 6, 1003–1010, 2-s2.0-84877629911, https://doi.org/10.1136/annrheumdis-2012-201750.
10.1136/annrheumdis-2012-201750
PubMed Web of Science® Google Scholar
10 Mangasarian O. L., Street W. N., and Wolberg W. H., Breast carter diagnosis and prognosis via linear programrnig, Operation Research. (1995) 43, no. 4.
10.1287/opre.43.4.570
Google Scholar
11 Golikov A. I., Evtushenko Y. G., and Ketabchi S., On families of hyperplanes that separate polyhedra, Computational Mathematics and Mathematical Physics. (2005) 45, no. 2, 238–253, 2-s2.0-33746628958.
Google Scholar
12 Alimov A. R. and Protasov V. Y., Separation of convex sets by extreme hyperplanes, Fundamental and Applied Mathematics. (2012) 17, no. 4, 3–12, 2-s2.0-84863898700.
Google Scholar
13 Eremin I. I., Fejér methods for the strong separability of convex polyhedral sets, Russian Mathematics. (2006) no. 12, 33–43.
Google Scholar
14 Ershova A. V., Algorithm of the disjoint convex polyhedral separating using Fejer mappings, Sistemi Upravlenia I Informacionnie Tehnologii. (2009) 1, no. 35, 53–56.
Google Scholar
15 Böhm C. and Kriegel H.-P., Determining the convex hull in large multidimensional databases, Data Warehousing and Knowledge Discovery, 2001, 2114, Springer, 294–306, Lecture Notes in Computer Science, https://doi.org/10.1007/3-540-44801-2_29.
10.1007/3-540-44801-2_29
Google Scholar
16 Fung G., Rosales R., and Krishnapuram B., Learning rankings via convex hull separation, Proceedings of the Annual Conference on Neural Information Processing Systems (NIPS ′05), December 2005, 395–402, 2-s2.0-79955069587.
Google Scholar
17 Kolmogorov A. N. and Fomin S. V., Elements of the Theory of Functions and Functional Analysis, 1999, Courier Dover.
Google Scholar
18 Altman D. G., Practical Statistics for Medical Research, 1991, Chapman & Hall/CRC, London, UK.
10.1136/bmj.328.7441.702
PubMed Google Scholar
19 Abramov S. A., Lectures at Algorithmic Complexity, 2009, MTSNMO, Moscow, Russia.
Google Scholar
20 Preparata F. and Shamos M., Computational Geometry—An Introduction, 1985, Springer.
10.1007/978-1-4612-1098-6
Google Scholar
21 Banks P. A. and Freeman M. L., Practice guidelines in acute pancreatitis, The American Journal of Gastroenterology. (2006) 101, no. 10, 2379–2400.
10.1111/j.1572-0241.2006.00856.x
PubMed Web of Science® Google Scholar
22 BradleyE. L.III and Frey C. F., A clinically based classification system for acute pancreatitis: summary of the International Symposium on Acute Pancreatitis, Atlanta, Ga, September 11 through 13, 1992, Archives of Surgery. (1993) 128, no. 5, 586–590, 2-s2.0-0027254390.
10.1001/archsurg.1993.01420170122019
PubMed Web of Science® Google Scholar

All articles

Mathematical Modeling of the Expert System Predicting the Severity of Acute Pancreatitis

Abstract

1. Introduction

2. Methods

2.1. Separation of the Convex Hulls

2.2. Modeling the Expert System of Predicting the Presence of Severity in Patients

3. Results

3.1. The Expert System of Predicting the Presence of Severity in Patients with Acute Pancreatitis

4. Conclusions

Conflict of Interests

References

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Mathematical Modeling of the Expert System Predicting the Severity of Acute Pancreatitis

Abstract

1. Introduction

2. Methods

2.1. Separation of the Convex Hulls

2.2. Modeling the Expert System of Predicting the Presence of Severity in Patients

3. Results

3.1. The Expert System of Predicting the Presence of Severity in Patients with Acute Pancreatitis

4. Conclusions

Conflict of Interests

References

Figures

References

Related

Information