Journal of Computational Methods in Physics

Volume 2014, Issue 1 512702

Research Article

Open Access

Spectral-Homotopy Perturbation Method for Solving Governing MHD Jeffery-Hamel Problem

Corresponding Author

Ahmed A. Khidir

[email protected]

Faculty of Technology of Mathematical Sciences and Statistics, Al-Neelain University, Algamhoria Street, P.O. Box 12702, Khartoum, Sudan neelain.edu.sd

Search for more papers by this author

Ahmed A. Khidir,

Corresponding Author

Ahmed A. Khidir

[email protected]

Faculty of Technology of Mathematical Sciences and Statistics, Al-Neelain University, Algamhoria Street, P.O. Box 12702, Khartoum, Sudan neelain.edu.sd

Search for more papers by this author

First published: 14 July 2014

https://doi.org/10.1155/2014/512702

Citations: 1

Academic Editor: Xavier Ferrieres

Share a link

Email
Wechat
Bluesky

Abstract

We present a new modification of the homotopy perturbation method (HPM) for solving nonlinear boundary value problems. The technique is based on the standard homotopy perturbation method and blending of the Chebyshev pseudospectral methods. The implementation of the new approach is demonstrated by solving the MHD Jeffery-Hamel flow and the effect of MHD on the flow has been discussed. Comparisons are made between the proposed technique, the previous studies, the standard homotopy perturbation method, and the numerical solutions to demonstrate the applicability, validity, and high accuracy of the presented approach. The results demonstrate that the new modification is more efficient and converges faster than the standard homotopy perturbation method at small orders. The MATLAB software has been used to solve all the equations in this study.

1. Introduction

The incompressible viscous fluid flow through convergent-divergent channels is one of the most applicable cases in fluid mechanics, civil, environmental, mechanical, and biomechanical engineering. The mathematical investigations of this problem were pioneered by Jeffery [1] and Hamel [2]. They presented an exact similarity solution of the Navier-Stokes equations in the special case of two-dimensional flow through a channel with inclined plane walls meeting at a vertex and with a source or sink at the vertex and have been extensively studied by several authors and discussed in many textbooks, for example, [3, 4]. In the Ph.D. thesis [5] we find that Jeffery-Hamel flow used as asymptotic boundary conditions to examine a steady of two-dimensional flow of a viscous fluid in a channel. But, here certain symmetric solutions of the flow has been considered by Sobey and Drazin [6]. Although asymmetric solutions are both possible and of physical interest.

The classical Jeffery-Hamel problem was extended by Axford [7] to include the effects of an external magnetic field on an electrically conducting fluid; in MHD Jeffery-Hamel problems there are two additional nondimensional parameters that determine the solutions, namely, the magnetic Reynolds number and the Hartmann number. Most scientific problems such as Jeffery-Hamel flows and other fluid mechanic problems are inherently in form of nonlinear differential equations. Except a limited number of these problems, most of them do not have exact solution and some of the solved by numerical methods. Therefore, these nonlinear equations should be solved using other methods. Therefore, many different methods have recently introduced some ways to obtain analytical solution for these nonlinear problems, such as the homotopy perturbation method (HPM) by He [8, 9], the homotopy analysis method (HAM) by Liao [10, 11], the adomian decomposition method (ADM) [12–14], the variational iteration method (VIM) by He [15], the differential transformation method by Zhou [16], and recently spectral homotopy analysis method (SHAM) by Motsa et al. [17]. In the numerical method, stability and convergence should be considered so as to avoid divergence or inappropriate results. Some of these methods used small parameter in the equation. Therefore, finding the small parameter and exerting it into the equation are deficiencies of these methods.

Nonnumerical approaches include the classical power-series method and its variants for systems of nonlinear differential equations with small or large embedded parameters such as the homotopy perturbation method. However, it is well-known that most of these perturbation solutions are not valid in the whole physical region. These methods do not guarantee the convergence of the series solution, and the perturbation approximations may be only valid for weakly nonlinear problems. Further disadvantages of perturbation methods are that (i) they require the presence of a large or small parameter in the problem while nonperturbation methods require a careful selection of initial approximations and linear operators and (ii) linearization usually leads to difficulties in the integration of higher order deformation equations.

In this work, we present an alternative and improved form of the HPM called spectral-homotopy perturbation method (SHPM) that blends the traditional homotopy perturbation method with the Chebyshev spectral collocation method. The advantage of this approach is that it is more flexible than HPM for choosing a linear operator and initial guess. In HPM, one is restricted to choosing a linear operator and initial approximation that would make the integration of the higher-order differential equations possible whereas the SHPM allows us to have a wider range of selecting linear operators and aninitial guess may be used as long as it satisfies the boundary conditions.

The aim of this study is to apply spectral homotopy perturbation method (SHPM) to find an approximate solution to the nonlinear differential equation governing MHD Jeffery-Hamel flow. We have made a comparison between the current results and other methods with the numerical solution. The results proves the applicability, accuracy, and efficiency of the (SHPM).

2. Mathematical Formulation

Consider the steady two-dimensional flow of an incompressible conducting viscous fluid from a source or sink at the intersection between two rigid plane walls that the angel between them is 2α. The grid walls are considered to be divergent if α > 0 and convergent if α < 0. We assume that the velocity is only along radial direction and depend on r and θ, where r and θ are radial and angular coordinates, respectively, so that v = (u(r, θ), 0) only as shown in Figure 1. Using continuity equation and Navier-Stokes equations in polar coordinates, one has

()

where P is the fluid pressure, B₀ is the electromagnetic induction, σ is the conductivity of the fluid, ρ is the fluid density, and ν is the coefficient of kinematic viscosity. From (1), one has

()

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Geometry of the MHD Jeffery-Hamel flow.

Using the dimensionless parameters

()

and with eliminating P from (2) and (3), we obtain the following ordinary differential equation for the normalized function profile F(η):

()

subject to the boundary conditions

()

where Re is the Reynolds number:

()

where U_max⁡ is the velocity at the center of the channel (r = 0) and

is the square of the Hartmann number. Now we solve (6) by using (SHPM).

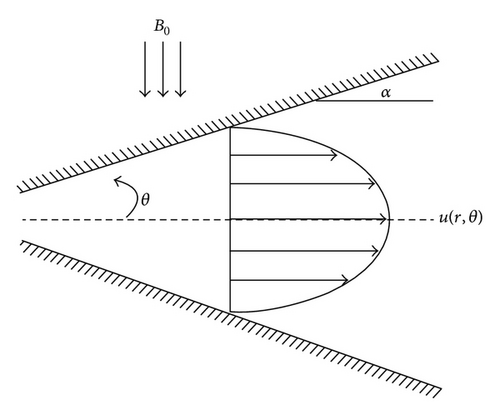
3. The Homotopy Perturbation Method

The homotopy perturbation method is a combination of the classical perturbation technique and homotopy technique. To illustrate the basic ideas of the HPM, we consider the following nonlinear differential equation:

()

with the boundary conditions

()

where A is a general operator, B is a boundary operator, f(r) is a known analytic function, and Γ is the boundary of the domain Ω.

The operator A can, generally speaking, be divided into two parts L and N, where L is linear, while N is nonlinear, (9), therefore can be written as follows:

()

By the homotopy technique (see [10, 11]), we construct a homotopy

wich satisfies

()

where p ∈ [0,1] is an embedding parameter and u₀ is an initial approximation of (9), wich satisfies the boundary conditions. Obviously, from (12) we have

()

The changing process of p from 0 to 1 is just that of v(r, p) from u₀(r) to u(r). In topology, this is called deformation, and L(v) − L(u₀), A(v) − f(r) are called homotopic.

According to HPM, we can first use the embedding parameter p as small parameter and assume that the solution of (12) can be written as a power series ip p4:

()

setting p = 1, results in the approximation to the solution of (9)

()

The series (16) is convergent for most cases; however, the convergent depends upon the nonlinear operator A(v). Some criteria suggested for convergence of the series (16) and the following opinions are suggested by He [18, 19].

(1)
The second derivative of N(v) with respect to v must be small because the parameter p may be relatively large, that is, p → 1.
(2)
The norm of L₋₁(∂N/∂v) must be smaller than one so that the series converges.

4. The Spectral Homotopy Perturbation Method

To solve the nonlinear ordinary differential equation (6) using the SHPM we start by transfom the domain of the problem from [0,1] to the domain [−1,1] on which the Chebyshev spectral method can be implemented, using the algebraic mapping

()

It is also convenient to make the boundary conditions homogeneous by making use of the transformation

()

Substituting (18) and (17) in (6) and the boundary conditions (7) gives

()

subject to

()

where

()

To apply the SHPM to the differential equation (19) we may choose the following linear differential operator:

()

The initial approximation for the solution of (19) is obtained from the solution to the linear part of (19). Consider

()

subject to the boundary conditions

()

If an exact solution of (23) cannot be found, we use the Chebyshev pseudospectral method to solve the equation. We now construct the homotopy:

()

where F is an approximate series solution of given by

()

And N(F) is the nonlinear part of (19). Substitute (22) in (25) to get

()

We make a comparison between the power of p¹ in both sides of (27) to obtain the following system of equations:

()

subject to the boundary conditions

()

where

()

where T denotes transpose, diag [] is a diagonal matrix of size (N + 1)×(N + 1), and

is the Chebyshev spectral differentiation matrix whose entries (see [20, 21]) are given by

()

Here c₀ = c_N = 2 and c_j = 1 with 1 ≤ j ≤ N − 1, x_j are the Chebyshev collocation points (see [20]) defined by

()

the solution of (28) can be given by

()

To get more higher order approximations for (19), we compare between the coefficients of pⁱ, (i = 2,3, 4, …) in (25) to obtain the following approximations:

()

subject to the boundary conditions

()

where

()

The matrix A has dimensions (N + 1)×(N + 1) while matrices B_i and f_i have a dimensions (N + 1) × 1.

To implement the boundary conditions (29) and (35) to the systems (28) and (34), respectively, we delete the first and the last rows and columns of A and delete the first and last rows of and f₁ and f_i; also we replace the results of last row of the modified matrix A and setting the results of last row of the modified matrices B₁ and B_i to be zero. Then the solution of (19) is given by substituting the series f_i in (26) after setting p = 1.

5. Results and Discussion

In this section we present the obtained results of the solutions for MHD Jeffery-Hame flow using the HPM, SHPM, and a numerical solution. Here we used the inbuilt MATLAB boundary value problems solver bvp4c for the numerical solution approach. In generating the presented results it was determined through numerical experimentation that N = 60. Table 1 shows a comparison between the HPM, SHPM, and numerical approximate solutions of F(η). The table shows that the results of the present method are in excellent agreement with those of the numerical ones. Also in Table 2 we give a comparison of the SHPM results for divergent and convergent channels and fixed values of H and Re when η is varied at different orders of approximation against the numerical results. It can be seen from Table 2 that SHPM results converge rapidly to the numerical solution. Table 3 gives a comparison of the differential transformation method (DTM), HPM, homotopy analysis method (HAM) given by Joneidi et al. [22], and SHPM results for F(η) against the numerical results when η is varied. It can be seen from this table that the approximate solution of MHD Jeffery-Hamel flows obtained by SHPM is very accurate and it is converges much more rapidly to the numerical result compared to the DTM, HPM, and HAM.

Table 1. Comparison between the HPM, SHPM, and numerical results of F(η) for different values of H when α = 7.5^° and Re = 50.

	η	0.1	0.2	0.3	0.4	0.5	0.6	0.7	0.8	0.9
H = 0	HPM	0.977071	0.911454	0.810411	0.685923	0.549843	0.413170	0.284602	0.170279	0.074423
	SHPM	0.977136	0.911454	0.810955	0.686840	0.551195	0.415007	0.286958	0.173044	0.076826
	Numeric	0.977136	0.911453	0.810954	0.686838	0.551193	0.415005	0.286957	0.173044	0.076826

H = 250	HPM	0.983734	0.936343	0.861689	0.765340	0.653396	0.531462	0.403813	0.272871	0.138943
	SHPM	0.983736	0.936343	0.861708	0.765375	0.653451	0.531542	0.403921	0.273000	0.139045
	Numeric	0.983736	0.936343	0.861708	0.765375	0.653451	0.531542	0.403921	0.273000	0.139045

H = 500	HPM	0.988320	0.953804	0.897852	0.822470	0.729682	0.620975	0.496664	0.355212	0.192382
	SHPM	0.988322	0.953804	0.897870	0.822501	0.729725	0.621028	0.496723	0.355266	0.192418
	Numeric	0.988322	0.953804	0.897870	0.822501	0.729725	0.621028	0.496723	0.355266	0.192418

H = 1000	HPM	0.993761	0.974806	0.942279	0.894743	0.829747	0.743476	0.629987	0.479934	0.278279
	SHPM	0.993765	0.974806	0.942318	0.894809	0.829843	0.743602	0.630138	0.480096	0.278418
	Numeric	0.993765	0.974806	0.942318	0.894809	0.829843	0.743602	0.630138	0.480096	0.278418

Table 2. Comparison of the values of the SHPM approximate solutions for F(η) with the numerical solution for various values of η when H = 100 and Re = 50 for divergent and convergent channels.

η	divergent-channel α = 5^°					convergent-channel α = −5^°
η	3rd order	4th order	6th order	8th order	Numerical	3rd order	4th order	6th order	8th order	Numerical
0.1	0.983499	0.983500	0.983500	0.983500	0.983500	0.994672	0.994672	0.994672	0.994672	0.994672
0.2	0.935285	0.935287	0.935286	0.935286	0.935286	0.978184	0.978184	0.978184	0.978184	0.978184
0.3	0.858989	0.858991	0.858991	0.858991	0.858991	0.948987	0.948986	0.948986	0.948986	0.948986
0.4	0.759953	0.759957	0.759957	0.759957	0.759957	0.904400	0.904399	0.904399	0.904399	0.904399
0.5	0.644378	0.644384	0.644384	0.644384	0.644384	0.840477	0.840475	0.840475	0.840475	0.840475
0.6	0.518442	0.518448	0.518448	0.518448	0.518448	0.751876	0.751874	0.751874	0.751874	0.751874
0.7	0.387576	0.387581	0.387581	0.387581	0.387581	0.631800	0.631798	0.631798	0.631798	0.631798
0.8	0.255978	0.255981	0.255981	0.255981	0.255981	0.472168	0.472166	0.472166	0.472166	0.472166
0.9	0.126379	0.126380	0.126380	0.126380	0.126380	0.264232	0.264231	0.264231	0.264231	0.264231

Table 3. Comparison between DTM, HPM, HAM, SHPM, and numerical solution of F(η) for various values of η when Re = 80, α = −5^°, and H = 0.

η	ADM	HPM	HAM	SHPM	Numerical
0.0	1	1	1	1	1
0.1	0.99596039	0.99606719	0.99596062	0.99596206	0.99596205
0.2	0.98327455	0.98369594	0.98327553	0.98328122	0.98328121
0.3	0.96017756	0.96107588	0.96017989	0.96019253	0.96019253
0.4	0.92351707	0.92492452	0.92352157	0.92354347	0.92354347
0.5	0.86845113	0.87019977	0.86845890	0.86849152	0.86849152
0.6	0.78807854	0.78983259	0.78809102	0.78813414	0.78813414
0.7	0.67312484	0.67453350	0.67314377	0.67319429	0.67319429
0.8	0.51196441	0.51283731	0.51199099	0.51204134	0.51204134
0.9	0.29152801	0.29189370	0.29155802	0.29159436	0.29159436
1.0	0.00000000	0.00000000	−0.00000115	0.00000000	0.00000000

Figures 2(a) and 2(b) show firstly the influence of the magnetic field parameter on the velocity profile for divergent and convergent channels and, secondly, a comparison between the present results and numerical results to give a sense of the accuracy and convergence rate of the SHPM. The figures indicate that there is very good match between the two sets of results even at very low orders of SHPM approximations series compared with the numerical results. These findings firmly establish the SHPM as an accurate and alternative to the HPM. Also it can seen that the fluid velocity increases with increasing Hartman numbers for both convergent and divergent channels.

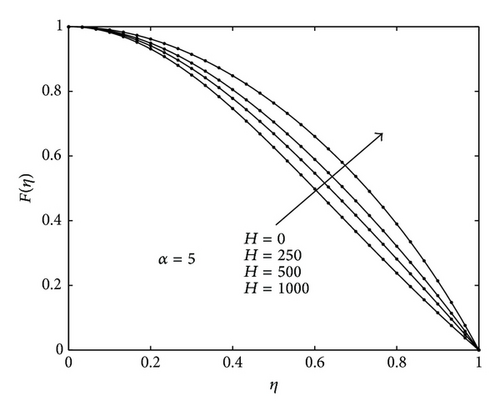
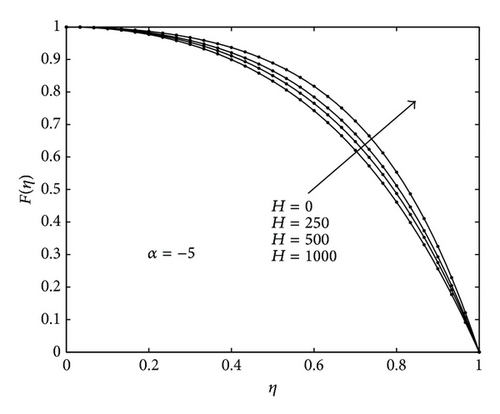
6. Conclusions

In this study, the SHPM were applied successfully to find an approximate solution of a nonlinear MHD Jeffery-Hamel flows. The effect of the magnetic field parameter on the velocity profile for convergent and divergent channels has been determined. It could be noticed that by increasing magnetic field parameter, the velocity profile increases resulting in a rise in the flow rate for both convergent and divergent channels. The obtained results compared with the numerical solution of the governing nonlinear equation and with DTM, HPM, and HAM. Also the tables and figures clearly show high accuracy of the method and the convergent is very fast to solve MHD Jeffery-Hamel problem. An important aspect of this work has been the need to prove the computational efficiency and accuracy of the SHPM in solving nonlinear differential equations and this method is, in general, more accurate than the HPM. The results in this paper confirm that the SHPM is a powerful and efficient technique for finding solutions for nonlinear differential equations in different fields of science and engineering.

Conflict of Interests

The author declares that there is no conflict of interests regarding the publication of this paper.

References

1 Jeffery G. B., The two-dimensional steady motion of a viscous fluid, Philosophical Magazine. (1915) 6, 455–465.
Google Scholar
2 Hamel G., Spiralförmige Bewegungen zäher Flüssigkeiten, Jahresbericht der Deutschen Mathematiker-Vereinigung. (1916) 25, 34–60.
Google Scholar
3 Rosenhead L., The steady two-dimensional radial flow of viscous fluid between two inclined plane walls, Proceedings of the Royal Society A. (1940) 175, 436–467.
Google Scholar
4 McAlpine A. and Drazin P. G., On the spatio-temporal development of small perturbations of Jeffery-Hamel flows, Fluid Dynamics Research. (1998) 22, no. 3, 123–138, https://doi.org/10.1016/S0169-5983(97)00049-X, MR1606157, 2-s2.0-0032033258.
10.1016/S0169-5983(97)00049-X
Web of Science® Google Scholar
5 Sadri R. M., Channel entrance flow [Ph.D. thesis], 1997, Department of Mechanical Engineering, the University of Western Ontario.
Google Scholar
6 Sobey I. J. and Drazin P. G., Bifurcations of two-dimensional channel flows, Journal of Fluid Mechanics. (1986) 171, 263–287, https://doi.org/10.1017/S0022112086001441, MR869513, ZBL0609.76050, 2-s2.0-0022925935.
Google Scholar
7 Axford W. I., The magnetohydrodynamic Jeffrey-Hamel problem for a weakly conducting fluid, The Quarterly Journal of Mechanics and Applied Mathematics. (1961) 14, 335–351, https://doi.org/10.1093/qjmam/14.3.335, MR0135794, ZBL0106.40801, 2-s2.0-77952521953.
Web of Science® Google Scholar
8 He J., A review on some new recently developed nonlinear analytical techniques, International Journal of Nonlinear Sciences and Numerical Simulation. (2000) 1, no. 1, 51–70, 2-s2.0-0002734020.
Google Scholar
9 He J. H., Homotopy perturbation method for bifurcation of nonlinear problems, International Journal of Nonlinear Sciences and Numerical Simulation. (2005) 8, no. 2, 207–208, 2-s2.0-17844387391.
Google Scholar
10 Liao S. J., The proposed homotopy analysis technique for the solution of nonlinear problems [Ph.D. thesis], 1992, Shanghai Jiao Tong University.
Google Scholar
11 Liao S., On the homotopy analysis method for nonlinear problems, Applied Mathematics and Computation. (2004) 147, no. 2, 499–513, https://doi.org/10.1016/S0096-3003(02)00790-7, MR2012589, 2-s2.0-0141961626.
10.1016/S0096-3003(02)00790-7
Web of Science® Google Scholar
12 Esmaili Q., Ramiar A., Alizadeh E., and Ganji D. D., An approximation of the analytical solution of the Jeffery-Hamel flow by decomposition method, Physics Letters A: General, Atomic and Solid State Physics. (2008) 372, no. 19, 3434–3439, https://doi.org/10.1016/j.physleta.2008.02.006, 2-s2.0-41949100052.
Google Scholar
13 Makinde O. D. and Mhone P. Y., Hermite-Padé approximation approach to MHD Jeffery-Hamel flows, Applied Mathematics and Computation. (2006) 181, no. 2, 966–972, https://doi.org/10.1016/j.amc.2006.02.018, ZBL1102.76049, 2-s2.0-33750451236.
Google Scholar
14 Makinde O. D., Effect of arbitrary magnetic Reynolds number on MHD flows in convergent-divergent channels, International Journal of Numerical Methods for Heat & Fluid Flow. (2008) 18, no. 5-6, 697–707, https://doi.org/10.1108/09615530810885524, MR2442633, 2-s2.0-48249148152.
Web of Science® Google Scholar
15 He J. H., Variational iteration method—a kind of non-linear analytical technique: Some examples, International Journal of Non-Linear Mechanics. (1999) 34, no. 4, 699–708, https://doi.org/10.1016/S0020-7462(98)00048-1, 2-s2.0-0000092673.
10.1016/S0020-7462(98)00048-1
Google Scholar
16 Zhou J. K., Differential Transformation and Its Applications for Electrical Circuits, 1986, Huazhong University Press, Wuhan, China, (Chinese).
Google Scholar
17 Motsa S. S., Sibanda P., Awad F. G., and Shateyi S., A new spectral-homotopy analysis method for the MHD Jeffery-Hamel problem, Computers & Fluids. (2010) 39, no. 7, 1219–1225, https://doi.org/10.1016/j.compfluid.2010.03.004, MR2645383, 2-s2.0-77952471075.
Google Scholar
18 He J. H., Homotopy perturbation technique, Computer Methods in Applied Mechanics and Engineering. (1999) 178, no. 3-4, 257–262, https://doi.org/10.1016/S0045-7825(99)00018-3, MR1711041, 2-s2.0-0032672778.
10.1016/S0045-7825(99)00018-3
Web of Science® Google Scholar
19 He J. H., A coupling method of a homotopy technique and a perturbation technique for non-linear problems, International Journal of Non-Linear Mechanics. (2000) 35, no. 1, 37–43, https://doi.org/10.1016/S0020-7462(98)00085-7, MR1723761, 2-s2.0-0033702384.
10.1016/S0020-7462(98)00085-7
Web of Science® Google Scholar
20 Trefethen L. N., Spectral Methods in MATLAB, 2000, SIAM.
Google Scholar
21 Don W. S. and Solomonoff A., Accuracy and speed in computing the Chebyshev collocation derivative, SIAM Journal on Scientific Computing. (1995) 16, no. 6, 1253–1268, https://doi.org/10.1137/0916073, MR1355492, ZBL0840.65010.
Google Scholar
22 Joneidi A. A., Domairry G., and Babaelahi M., Three analytical methods applied to Jeffery-Hamel flow, Communications in Nonlinear Science and Numerical Simulation. (2010) 15, no. 11, 3423–3434, https://doi.org/10.1016/j.cnsns.2009.12.023, 2-s2.0-77952238986.
Google Scholar

Citing Literature

All articles

Spectral-Homotopy Perturbation Method for Solving Governing MHD Jeffery-Hamel Problem

Abstract

1. Introduction

2. Mathematical Formulation

3. The Homotopy Perturbation Method

4. The Spectral Homotopy Perturbation Method

5. Results and Discussion

6. Conclusions

Conflict of Interests

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Spectral-Homotopy Perturbation Method for Solving Governing MHD Jeffery-Hamel Problem

Abstract

1. Introduction

2. Mathematical Formulation

3. The Homotopy Perturbation Method

4. The Spectral Homotopy Perturbation Method

5. Results and Discussion

6. Conclusions

Conflict of Interests

References

Citing Literature

Figures

References

Related

Information