Volume 2014, Issue 1 485630

Research Article

Open Access

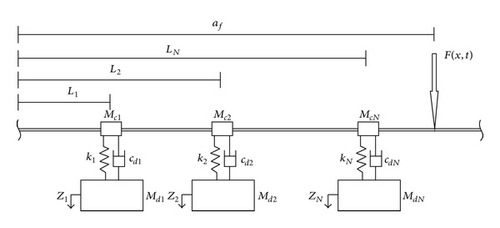
On the Dynamic Analysis of a Beam Carrying Multiple Mass-Spring-Mass-Damper System

Correction(s) for this article

O. Barry,

Corresponding Author

O. Barry

[email protected]

Department of Mechanical and Industrial Engineering, University of Toronto, Toronto, ON, Canada M5S 3G8, utoronto.com

Search for more papers by this author

D. C. D. Oguamanam,

D. C. D. Oguamanam

Department of Mechanical and Industrial Engineering, Ryerson University, Toronto, ON, Canada M5B 2K3, ryerson.ca

Search for more papers by this author

J. W. Zu,

J. W. Zu

Department of Mechanical and Industrial Engineering, University of Toronto, Toronto, ON, Canada M5S 3G8, utoronto.com

Search for more papers by this author

O. Barry,

Corresponding Author

O. Barry

[email protected]

Department of Mechanical and Industrial Engineering, University of Toronto, Toronto, ON, Canada M5S 3G8, utoronto.com

Search for more papers by this author

D. C. D. Oguamanam,

D. C. D. Oguamanam

Department of Mechanical and Industrial Engineering, Ryerson University, Toronto, ON, Canada M5B 2K3, ryerson.ca

Search for more papers by this author

J. W. Zu,

J. W. Zu

Department of Mechanical and Industrial Engineering, University of Toronto, Toronto, ON, Canada M5S 3G8, utoronto.com

Search for more papers by this author

First published: 2014

https://doi.org/10.1155/2014/485630

Citations: 12

Academic Editor: Jeong-Hoi Koo

Share a link

Email
Wechat
Bluesky

Abstract

The exact natural frequencies, mode shapes, and the corresponding orthogonality relations are important in forced vibration analysis via modal expansion. In the present paper, a free vibration analysis is conducted to determine the exact natural frequencies and mode shapes of an axially loaded beam carrying several absorbers. An explicit expression is presented for the generalized orthogonality relations. These generalized orthogonality conditions are employed along with the assumed modes method to perform forced vibration analysis. The present approach is compared to other approximate methods in the literature with the classical orthogonality relations and different choice of mode shapes. The results indicate that the use of the generalized orthogonality relation with the exact mode shapes is required for a precise investigation of the dynamic response of a beam with mass-spring-mass-damper system.

1. Introduction

The study of beam vibrations is attracting continued interest all these years because of the wide range of engineering applications involving beams. Beam models are used to idealize buildings components, bridges, overhead transmission lines, microelectromechanical systems, and many more. In the case of overhead transmission lines a single conductor may be modeled as a beam that is subjected to a tensile load with the damper represented as a mass-spring-damper-mass system.

Numerous authors have studied the free and/or forced response of beams carrying in-span mass or spring-mass systems. In most investigations on the free vibration, different authors have used analytical methods to determine the exact solutions for the natural frequencies and mode shapes (e.g., [1–13] and references mentioned therein).

There are, however, few published exact solutions of the forced vibration problems. The most common analytical approach used in forced vibration analysis is based on the assumed modes method in conjunction with the classical orthogonality conditions which may be expressed as $\int_{0}^{L} Y_{i} Y_{j} d x = δ_{i j}$ , where L is the length of the beam, Y_i and Y_j are the ith and jth normal mode shapes, respectively, and δ_ij is the Kronecker delta function. Hereinafter a beam without mass or spring-mass system is referred to as a bare beam, or else it is called a loaded beam.

In [14–16], the authors employed the mode shapes of the bare beam and the classical orthogonality condition to study the forced response of loaded beams. Combinations of the mode shapes of the loaded beam with the classical orthogonality relation were employed in [17–23]. These two approaches are simple and easy to implement and, in some cases, give very good approximations. However, it was shown in [21, 24] that the mode shapes of the loaded beam and those of the bare beam are different. Further, Hassanpour et al. [25] showed that the mode shapes of the loaded beam were not orthonormal under the classical orthogonality conditions. They also presented the generalized orthogonality conditions for an axially loaded beam with in-span concentrated mass and springs. The study ignored the case where a suspended mass is connected to the beam via a spring-dashpot system.

The majority of the studies reported in the literature focused on the study of beams with either an in-span mass or spring-mass system. A series combination of each type was found in some cases. However, works that simultaneously examined the free and forced vibration of a beam with multiple in-span mass-spring-damper-mass systems and subjected to an axial force were not found. The investigation of this problem is reported in the present paper; it is an extension of the work presented in [13]. The exact natural frequencies and mode shapes are determined and explicit expressions are presented for the orthogonality relations. Parametric studies are used to examine the effect of the magnitude and location of the in-span mass-spring-damper-mass system on the natural frequencies and vibrational response. The effect of the use of the classical orthogonality condition is also examined. The results are validated using the finite element method and results from the literature.

2. Equations of Motion

A schematic of a beam with several in-span mass-spring-damper-mass systems is depicted in Figure 1. The system kinetic energy 𝒯 and potential energy 𝒱 may be expressed as

\begin{matrix} 𝒯 = \sum_{i = 1}^{N} (\frac{1}{2} m \int_{L_{i - 1}}^{L_{i}} {\dot{w}}_{i}^{2} (x, t) d x + \frac{1}{2} M_{d i} {\dot{z}}_{i}^{2} + \frac{1}{2} M_{c i} {\dot{z}}_{0 i}^{2}), \\ 𝒱 = \sum_{i = 1}^{N} (\frac{1}{2} E I \int_{L_{i - 1}}^{L_{i}} w_{i}^{'' 2} (x, t) d x + \frac{1}{2} c_{d i} {({\dot{z}}_{0 i} - {\dot{z}}_{i})}^{2} + \frac{1}{2} k_{i} {(z_{0 i} - z_{i})}^{2} + \frac{1}{2} T \int_{L_{i - 1}}^{L_{i}} w_{i}^{' 2} (x, t) d x), \end{matrix}

(1)

where z_0i(t) = w_i(L_i, t), EI is the beam flexural rigidity, m is the mass per unit length of the beam, and T is the beam pretension. The overdots and primes denote temporal and spatial derivatives, respectively. The subscript “i” denotes the position of the mass-spring-damper-mass system and “N” is the total number of attached mass-spring-damper-mass systems. The beam is assumed to be uniform and the pretension is constant.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Schematic of an axial beam carrying several mass-spring-damper-mass systems.

Introducing these energies equations into Hamilton’s principle and adding the forcing term F(x, t) yield the equations of motion and continuity conditions:

\begin{matrix} E I w_{i}^{''''} + m {\ddot{w}}_{i} - T w_{i}^{''} = F (x, t), \end{matrix}

(2)

\begin{matrix} M_{d i} \ddot{z} + k_{i} (z_{i} - z_{0 i}) + c_{d i} ({\dot{z}}_{i} - {\dot{z}}_{0 i}) = 0, \end{matrix}

(3)

\begin{matrix} w_{i} (L_{i}, t) = w_{i + 1} (L_{i}, t), \end{matrix}

(4)

\begin{matrix} w_{i}^{'} (L_{i}, t) = w_{i + 1}^{'} (L_{i}, t), \end{matrix}

(5)

\begin{matrix} w_{i}^{''} (L_{i}, t) = w_{i + 1}^{''} (L_{i}, t) - M_{c i} {\ddot{z}}_{0 i} + E I w_{i}^{'''} (L_{i}, t) - T w_{i}^{'} (L_{i}, t) - k_{i} (z_{0 i} - z_{i}) - c_{d i} ({\dot{z}}_{0 i} - {\dot{z}}_{i}), \end{matrix}

(6)

\begin{matrix} - E I w_{i + 1}^{'''} (L_{i}, t) + T w_{i + 1}^{'} (L_{i}, t) = 0 . \end{matrix}

(7)

3. Frequency Equation and Mode Shapes

The deformations w_i(x_i, t) and displacements z(t) are expressed as

\begin{matrix} w_{i} (x_{i}, t) = L W_{i} (ζ) e^{ω t}, \\ z_{i} (t) = L A_{i} e^{ω t}, \end{matrix}

(8)

where W_i(ζ_i) and A_i are the respective nondimensional amplitudes of w_i(x_i, t) and z_i(t) and ω is the circular complex natural frequency of the system. Substituting (8) into (2)–(7) yields the following nondimensional system equations:

\begin{matrix} W_{i}^{''''} (ζ_{i}) - s^{2} W_{i}^{''} (ζ_{i}) + Ω^{4} W_{i} ζ_{i} = 0, \end{matrix}

(9)

\begin{matrix} A_{i} - K_{i} W_{i} (ξ_{i}) = 0, \end{matrix}

(10)

where

\begin{matrix} W_{i} (ζ_{i}) = c_{1 i} \sin α ζ_{i} + c_{2 i} \cos α ζ_{i} + c_{3 i} \sinh β ζ_{i} + c_{4 i} \cosh β ζ_{i} . \end{matrix}

(11)

Substituting (8) into (3)–(7) yields

\begin{matrix} W_{i} (ξ_{i}) = W_{i + 1} (ξ_{i}), \end{matrix}

(12)

\begin{matrix} W_{i}^{'} (ξ_{i}) = W_{i + 1}^{'} (ξ_{i}), \end{matrix}

(13)

\begin{matrix} W_{i}^{''} (ξ_{i}) = W_{i + 1}^{''} (ξ_{i}), \end{matrix}

(14)

\begin{matrix} W_{i}^{'''} (ξ_{i}) - W_{i + 1}^{'''} (ξ_{i}) - η_{i} W_{i} (ξ_{i}) + γ_{i} A_{i} = 0, \end{matrix}

(15)

where the following nondimensional variables are used:

\begin{matrix} ξ_{i} = \frac{L_{i}}{L}, A_{i} = K W_{i} (ξ_{i}), \\ K_{i} = \frac{k_{i} + ω c_{d i}}{k_{i} + M_{d i} ω^{2} + ω c_{d i}}, s^{2} = \frac{T L^{2}}{E I}, \\ Ω^{4} = \frac{m ω^{2}}{E I} L^{4}, η_{i} = \frac{k_{i} + ω^{2} M_{c i} + ω c_{d i}}{E I} L^{3}, \\ γ_{i} = \frac{k_{i} + ω c_{d i}}{E I} L^{3}, ζ = \frac{x}{L}, \\ \begin{matrix} α = \sqrt{- \frac{s^{2}}{2} + \sqrt{\frac{s^{4}}{4} + Ω^{4}}}, \end{matrix} β = \sqrt{\frac{s^{2}}{2} + \sqrt{\frac{s^{4}}{4} + Ω^{4}}} . \end{matrix}

(16)

Substituting (10) into (15) yields

\begin{matrix} W_{i}^{'''} (ξ_{i}) - W_{i}^{'''} (ξ_{i}) + W_{i} (ξ_{i}) (K_{i} γ_{i} - η_{i}) = 0 . \end{matrix}

(17)

The use of any classical boundary conditions at each end of the beam along with (12)–(14) and (17) yields a set of 4 + 4N algebraic homogeneous equations (4 equations from the boundary condition at the ends and 4N equations from the continuity relations). These algebraic equations are linear in the unknown coefficients (C’s) and they can be presented in matrix format as

\begin{matrix} {[ℱ]}_{(44 + N) X (44 + N)} {C}_{(44 + N) X (1)} = {0}_{(44 + N) X (1)}, \end{matrix}

(18)

where the elements of the matrix ℱ are listed in the Appendix. A nontrivial solution is obtained when matrix ℱ is singular. Hence, the characteristic or frequency equation is obtained as

\begin{matrix} \det ({[ℱ]}_{(44 + N) X (44 + N)}) = 0 . \end{matrix}

(19)

The mode shapes associated with each beam segment are obtained by substituting the integration constants from (18) into (11). An example of a matrix that yields the frequency equation is provided in the Appendix for the case of a cantilever beam with one in-span mass-spring-damper-mass support.

4. Generalized Orthogonality Relations

The solution of the equations of motion, (2) and (3), can be expressed as

\begin{matrix} w_{i} (x, t) = Y_{i} {(x)}^{(r)} e^{ω t}, \\ z_{i} (t) = Z_{i}^{(r)} e^{ω t}, \end{matrix}

(20)

where the superscript “r” denotes the mode number and

\begin{matrix} Y_{i} (x) = L W_{i} (ζ), \\ Z_{i} = L A_{i} . \end{matrix}

(21)

Substituting (20) into (3) and multiplying the resulting equation by Z^(s) yield

\begin{matrix} k_{i} Z_{i}^{(r)} Z_{i}^{(s)} + M_{d i} ω_{r}^{2} Z_{i}^{(r)} Z_{i}^{(s)} + ω_{r} c_{d i} Z_{i}^{(r)} Z_{i}^{(s)} = Y_{i}^{* (r)} Z_{i}^{(s)} (k_{i} + ω_{r} c_{d i}), \end{matrix}

(22)

where

Y_{i}^{* (r)} = Y_{i}^{(r)} (ξ_{1})

, Interchanging “r” and “s” in (22) and subtracting the resulting equation from (22) yield

\begin{matrix} (ω_{r}^{2} - ω_{s}^{2}) M_{d i} Z_{i}^{(r)} Z_{i}^{(s)} + c_{d i} (ω_{r} - ω_{s}) Z_{i}^{(r)} Z_{i}^{(s)} = k_{i} (Y_{i}^{* (r)} Z_{i}^{(s)} - Y_{i}^{* (s)} Z_{i}^{(r)}) + c_{d i} (ω_{r} Y_{i}^{* (r)} Z_{i}^{(s)} - ω_{s} Y_{i}^{* (s)} Z_{i}^{(r)}) . \end{matrix}

(23)

With reference to the equations of motion of the beam, substituting (20) into (2), then multiplying the resulting equation by Y^(s), and integrating over the entire length of the beam, as well as applying the continuity conditions, (12)–(15), with any classical boundary conditions except those for free ends yield

\begin{matrix} ω_{r}^{2} \sum_{i = 1}^{N} (m \int_{0}^{L_{i}} Y_{i}^{(r)} Y_{i}^{(s)} d x + M_{c i} Y_{i}^{* (r)} Y_{i}^{* (s)}) + ω_{r} \sum_{i = 1}^{N} c_{d i} Y_{i}^{* (r)} Y_{i}^{* (s)} = - \sum_{i = 1}^{N} (E I \int_{0}^{L_{i}} Y_{i}^{'' (r)} Y_{i}^{'' (s)} d x + T \int_{0}^{L_{i}} Y_{i}^{' (r)} Y_{i}^{' (s)} d x + k_{i} Y_{i}^{* (r)} Y_{i}^{* (s)} - k_{i} Z_{i}^{(r)} Y_{i}^{* (s)} - c_{d i} ω_{r} Z_{i}^{(r)} Y_{i}^{* (s)}) . \end{matrix}

(24)

Rewriting (24) and interchanging “r” and “s” yield

\begin{matrix} ω_{s}^{2} \sum_{i = 1}^{N} (m \int_{0}^{L_{i}} Y_{i}^{(s)} Y_{i}^{(r)} d x + M_{c i} Y_{i}^{* (s)} Y_{i}^{* (r)}) + ω_{s} \sum_{i = 1}^{N} c_{d i} Y_{i}^{* (s)} Y_{i}^{* (r)} = - \sum_{i = 1}^{N} (E I \int_{0}^{L_{i}} Y_{i}^{'' (s)} Y_{i}^{'' (r)} d x + T \int_{0}^{L_{i}} Y_{i}^{' (s)} Y_{i}^{' (r)} d x + k_{i} Y_{i}^{* (r)} Y_{i}^{* (s)} - k_{i} Z_{i}^{(s)} Y_{i}^{* (r)} - c_{d i} ω_{s} Z_{i}^{(s)} Y_{i}^{* (r)}) . \end{matrix}

(25)

Subtracting (25) from (24) and substituting (23) into the resulting equation yield

\begin{matrix} (ω_{r}^{2} - ω_{s}^{2}) \sum_{i = 1}^{N} (m \int_{0}^{L_{i}} Y_{i}^{(r)} Y_{i}^{(s)} d x + M_{c i} Y_{i}^{* (r)} Y_{i}^{* (s)} + M_{d i} Z_{i}^{(r)} Z_{i}^{(s)}) + (ω_{r} - ω_{s}) \sum_{i = 1}^{N} c_{d i} (Y_{i}^{* (r)} Y_{i}^{* (s)} + Z_{i}^{(r)} Z_{i}^{(s)}) = 0 . \end{matrix}

(26)

From (26), the first set of orthogonality relation is obtained as

\begin{matrix} \sum_{i = 1}^{N} (m \int_{0}^{L_{i}} Y_{i}^{(r)} Y_{i}^{(s)} d x + M_{c i} Y_{i}^{* (r)} Y_{i}^{* (s)} + M_{d i} Z_{i}^{(r)} Z_{i}^{(s)}) = δ_{r s}, \end{matrix}

(27)

where δ_rs is the Kronecker delta. The second set of orthogonality relation is expressed as

\begin{matrix} \sum_{i = 1}^{N} (Y_{i}^{* (r)} Y_{i}^{* (s)} + Z_{i}^{(r)} Z_{i}^{(s)}) = δ_{r s} . \end{matrix}

(28)

The use of (22) and (25) with the aid of some algebraic manipulation yields the third and fourth set of orthogonality relation. This may be written as

\begin{matrix} \sum_{i = 1}^{N} (E I \int_{0}^{L_{i}} Y_{i}^{'' (r)} Y_{i}^{'' (s)} d x + T \int_{0}^{L_{i}} Y_{i}^{' (r)} Y_{i}^{' (s)} d x) + \sum_{i = 1}^{N} k_{i} (Y_{i}^{* (r)} Y_{i}^{* (s)} - Z_{i}^{(s)} Y_{i}^{* (r)} - Z_{i}^{(r)} Y_{i}^{* (s)} + Z_{i}^{(r)} Z_{i}^{(s)}) = δ_{r s}, \end{matrix}

(29)

\begin{matrix} \sum_{i = 1}^{N} (Y_{i}^{* (r)} Z_{i}^{* (s)} + Z_{i}^{(r)} Y_{i}^{(s)}) = δ_{r s} . \end{matrix}

(30)

5. Forced Vibration

Assume a harmonic force F(x, t) is arbitrarily applied along the span of the beam as depicted in Figure 1. The response of the loaded beam is now derived using the generalized orthogonality relations (27)–(30). Let the excitation force be applied at a location a_f from the left-hand end on the beam; the governing equations of motion are now

\begin{matrix} m {\ddot{w}}_{i} + E I w_{i}^{''''} - T w_{i}^{''} = F (x, t) δ (x - a_{f}), \end{matrix}

(31)

\begin{matrix} M_{d i} {\ddot{z}}_{i} + k_{i} (z_{i} - w_{i} (L_{i})) + c_{d i} ({\dot{z}}_{i} - {\dot{w}}_{i} (L_{i})) = 0 . \end{matrix}

(32)

Using the assumed mode method, the transverse displacement of the beam and the displacement of vibration absorber may be expressed as

\begin{matrix} w_{i} = \sum_{r = 1}^{N_{r}} q_{r} (t) Y_{i}^{(r)} (x), \end{matrix}

(33)

\begin{matrix} z_{i} = \sum_{r = 1}^{N_{r}} q_{r} (t) Z_{i}^{(r)}, \end{matrix}

(34)

where N_r is the number of retained modes,

Y_{i}^{(r)} (x)

is the mode shape corresponding to the rth mode,

Z_{i}^{(r)}

is the displacement amplitude of the absorber, and q_r(t) is the rth generalized coordinate. Substituting (33) and (34) into (31) and (32), respectively, yields

\begin{matrix} m_{c} \sum_{r = 1}^{N_{r}} {\ddot{q}}_{r} Y_{i}^{(r)} + E I \sum_{r = 1}^{N_{r}} q_{r} Y_{i}^{'''' (r)} - T \sum_{r = 1}^{N_{r}} q_{r} Y_{i}^{'' (r)}, = F (t) δ (x - a_{f}) \\ M_{d i} \sum_{r = 1}^{N_{r}} {\ddot{q}}_{r} Y_{m i}^{(r)} + k_{i} \sum_{r = 1}^{N_{r}} q_{r} (Z_{i}^{(r)} - Y_{c i}^{(r)} (L_{i})) + c_{d i} \sum_{r = 1}^{N_{r}} {\dot{q}}_{r} (Z_{i}^{(r)} - Y_{c i}^{(r)} (L_{i})) = 0 . \end{matrix}

(35)

Multiplying (35) by

Y_{i}^{(s)}

and

Z_{i}^{(s)}

, respectively, adding the two resulting equations, integrating over the entire length of the beam, and applying the continuity conditions, (12)–(15), with any classical boundary conditions (except for free ends) yield

\begin{matrix} \sum_{r = 1}^{N_{r}} {\ddot{q}}_{r} {m \int_{0}^{L_{i}} Y_{i}^{(r)} Y_{i}^{(s)} d x + M_{c i} Y_{i}^{* (r)} Y_{i}^{* (s)} + M_{d i} Z_{i}^{(r)} Z_{i}^{(s)}} + c_{d i} \sum_{r = 1}^{N_{r}} {\dot{q}}_{r} {Y_{i}^{* (r)} Y_{i}^{* (s)} - Z_{i}^{(s)} Y_{i}^{* (r)} - Z_{i}^{(r)} Y_{i}^{* (s)} + Z_{i}^{(r)} Z_{i}^{(s)}} + \sum_{r = 1}^{N_{r}} q_{r} \{\int_{0}^{L_{i}} (E I Y_{i}^{'' (r)} Y_{i}^{'' (s)} + T Y_{i}^{' (r)} Y_{i}^{' (s)}) d x + k_{i} (Y_{i}^{* (r)} Y_{i}^{* (s)} - Z_{i}^{(s)} Y_{i}^{* (r)} - Z_{i}^{(r)} Y_{i}^{* (s)} + Z_{i}^{(r)} Z_{i}^{(s)})\} = F (x, t) Y_{i}^{(s)} (a_{f}) . \end{matrix}

(36)

Use of the orthogonality relations, (27)–(30), yields the following uncoupled differential equation:

\begin{matrix} [M_{r r}] {{\ddot{q}}_{r}} + [C_{r r}] {{\dot{q}}_{r}} + [K_{r r}] {q_{r}} = {F_{r}}, \end{matrix}

(37)

where the matrices M_rr, C_r, and K_rr are expressed as

\begin{matrix} M_{r r} = \sum_{i = 1}^{N} (m \int_{0}^{L_{i}} Y_{i}^{(r)^{2}} d x + M_{c i} Y_{i}^{* (r)^{2}} + M_{d i} Z_{i}^{(r)^{2}}), \\ C_{r r} = \sum_{i = 1}^{N} c_{d i} {(Y_{i}^{* (r)} - Z_{i}^{(r)})}^{2}, \\ K_{r} = \sum_{i = 1}^{N} {\int_{0}^{L_{i}} (E I Y_{i}^{'' (r)^{2}} + T Y_{i}^{' (r)^{2}}) d x + k_{i} {(Y_{i}^{* (r)} - Z_{i}^{(r)})}^{2}}, \\ F_{r} = F (x, t) Y_{i}^{(r)} (a_{f}) . \end{matrix}

(38)

The amplitude of the vibration absorber can be readily expressed as

\begin{matrix} Z_{i}^{(r)} = κ_{i} Y_{i}^{* (r)}, \\ κ_{i} = {(\frac{1 + {(2 ς_{i} r_{i})}^{2}}{{(1 - r_{i}^{2})}^{2} + {(2 ς_{i} r_{i})}^{2}})}^{1 / 2}, ς_{i} = \frac{c_{d i}}{2 M_{d i} ω_{s i}}, \\ r_{i} = \frac{Ω}{ω_{s i}}, ω_{s i} = \sqrt{\frac{k_{i}}{M_{d i}}} . \end{matrix}

(39)

6. Numerical Simulation

The sets of parameters employed in the numerical examples are taken from [1, 16]; they are tabulated in Table 1. The validity of the free vibration of the present model is inferred from the results tabulated in Table 2. In the case of a cantilevered beam with three spring-mass-damper systems, the first five natural frequencies of the present model are compared to those of [16]. The results show very good agreement with a maximum error of 0.28%.

Table 1. Material properties and parameters.

Parameter	Reference [1]	Reference [16]	Units
EI	63476.1	36.4583	Nm²
L	1.0	1.0	m
m	15.385	0.675	kg/m
m₁	3.0775	0.1	kg
m₂	4.614	0.1	kg
m₃	7.69	0.1	kg
m₄	9.997	—	kg
m₅	15.38	—	kg
k₁	190428	0.1	N/m
k₂	222166	0.1	N/m
k₃	285642.45	0.1	N/m
k₄	317380	—	N/m
k₅	380856	—	N/m
c_d1, c_d2, c_d3	—	0.1	Ns/m

Table 2. Natural frequency validation (rad/s).

Mode	Cantilevered		Pinned-pinned
	3 spring-mass-damper		3 spring-mass		5 spring-mass
	Reference [16]	Present	Reference [1]	Present	Reference [1]	Present
1	− 0.367 ± 25.8769i	− 0.367 ± 25.8544i	152.7339	152.7339	150.9571	150.9571
2	− 0.274 ± 161.7655i	− 0.275 ± 161.9399i	185.0949	185.0949	169.4728	169.4728
3	− 0.031 ± 452.1367i	− 0.031 ± 452.4320i	247.8313	247.8313	187.9146	187.9146
4	− 0.171 ± 887.2157i	− 0.174 ± 887.3469i	677.5959	677.5959	217.1278	217.1278
5	− 0.081 ± 1467.5170i	− 0.082 ± 1468.8356i	2548.6572	2548.6572	247.9867	247.9867

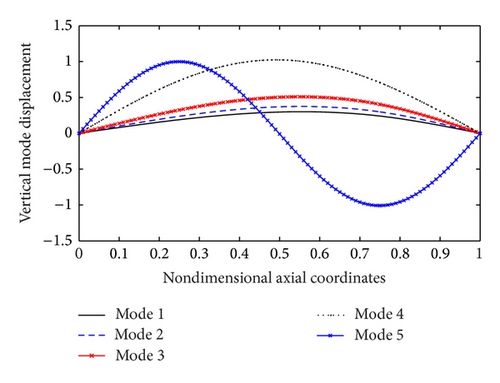
With respect to a pinned-pinned beam with attached three and five spring-mass systems, the validation is done via [1] and shows excellent agreement with four decimal places. The corresponding mode shapes for a beam carrying the three in-span spring-mass systems are depicted in Figure 2. This figure is identical to Figure 3 from [1].

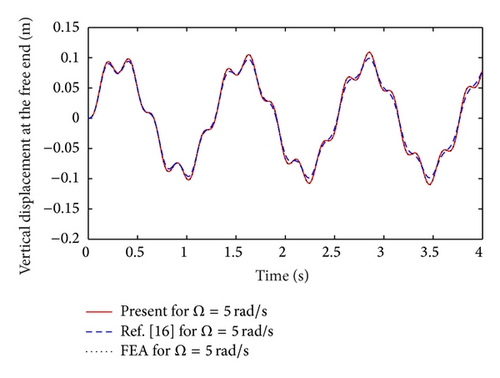
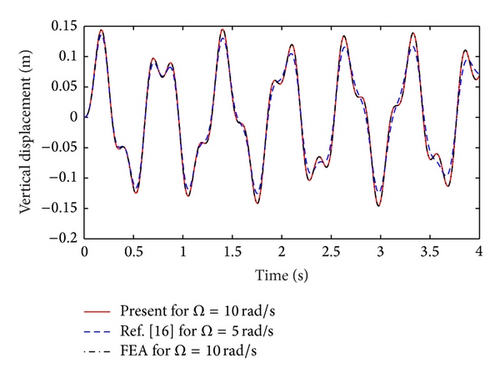
For the forced vibration simulations, an excitation force of F(t) = 10sin⁡(Ωt) is used with zero initial conditions. The force is first applied at the free end of a cantilevered beam with three identical spring-mass-damper systems located at 0.1, 0.5, and 0.9 m from the clamp end. The time history of the vertical displacement of the free end is presented to serve for comparison between the proposed approach (i.e., the combination of the generalized orthogonality conditions with the exact mode shapes of the loaded beam), the finite element method (FEM), and the approach used in [16]. The results are depicted in Figures 3 and 4 for an excitation frequency of 5 and 10 rad/s, respectively. All three methods are in agreement, but the FEM results agree better with the present approach than that of [16].

The frequency response curves for a simply supported beam with one in-span mass-spring-damper-mass system attached at 0.1 m from one end using three approaches are depicted in Figure 5. The first approach, which is the most accurate [25], employs the generalized orthogonality conditions along with the mode shapes of the loaded beam. The classical orthogonality relations and the mode shapes of the loaded beam are employed in the second approach, such as in [17–20]. The third method also uses the classical orthogonality conditions, but the mode shapes are those of the bare beam (see [14–16]). All three approaches yield very different midspan vertical displacements. The first approach is the exact solution and hence the error associated with the difference is defined with respect to the first approach. The frequency response amplitude errors are depicted in Figure 6 where the error can be as high as 10⁴.

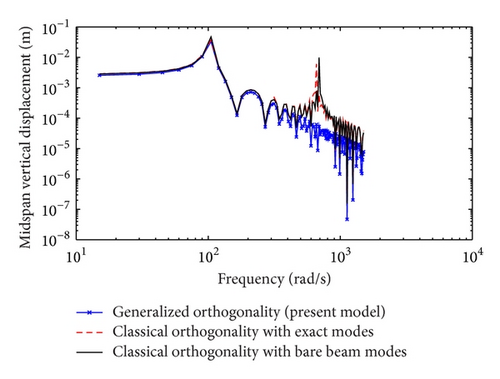
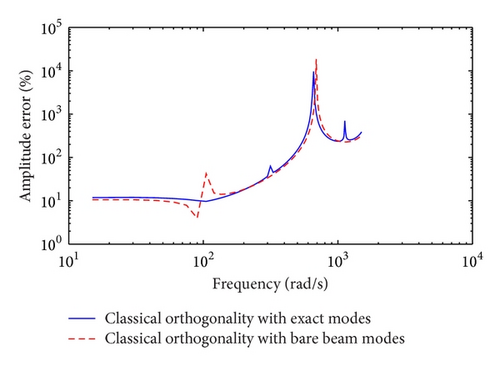
Figure 7 is an identical plot to Figure 5 with the pinned-pinned configuration replaced by a guided-guided one. The corresponding frequency response amplitude error is shown in Figure 8. The maximum amplitude error for the guided-guided beam is higher than that for the simply supported beam. A similar observation with regard to the discrepancy associated with the use of the classical orthogonality was reported in [25] for a simply supported beam carrying a heavy mass. An error as high as 10⁵ was reported.

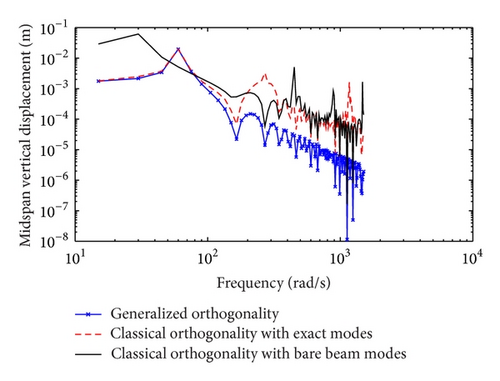
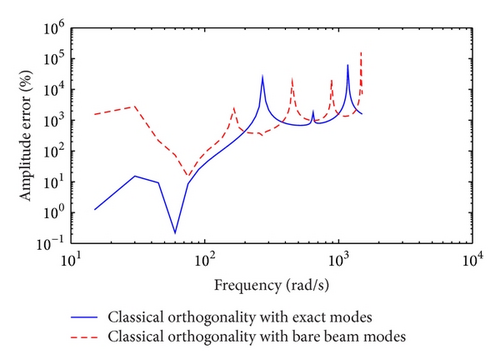
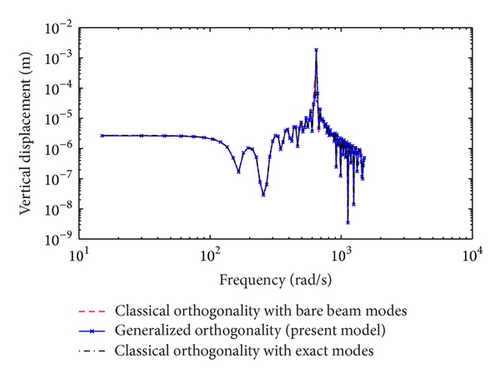
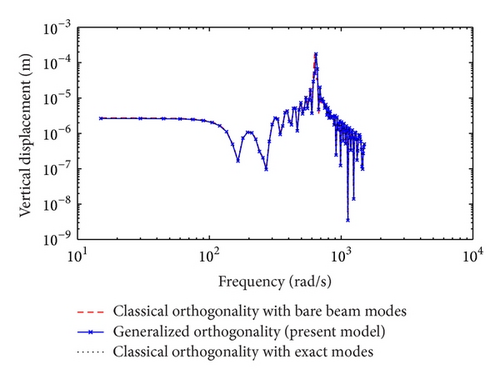
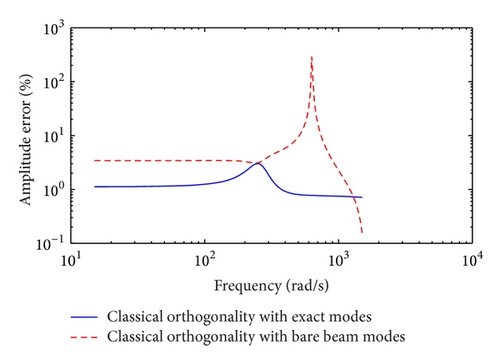
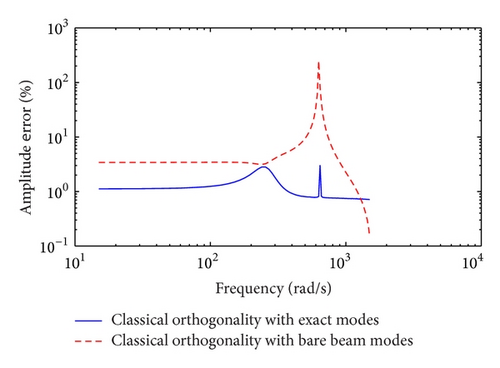
The three approaches are also examined using the parameters taken from [1] for a simply supported beam with one in-span mass-spring-damper system and no tension. Figures 9 and 10 show the frequency response of the midspan displacement for a damping coefficient c_di = 0.1 Ns/m and c_di = 100 Ns/m, respectively. It can be observed that all three methods yield very similar results and the plots are barely distinguishable. The amplitude errors associated with the results presented in Figures 9 and 10 are depicted in Figures 11 and 12, respectively. But for excitation frequencies closer to 600 rad/s the results indicate very minimal error. The discrepancy is more pronounced in the case of the classical orthogonality with the combination of the bare beam mode shapes.

7. Conclusions

A common approach to studying the vibrational response of an elastically loaded beam involves the use of the classical orthogonality relations along with the mode shapes of the bare beam. It has been shown, however, that the mode shapes of the bare beam can be quite different from those of the loaded beam. In the present paper, the exact natural frequencies and mode shapes were presented for an axially loaded beam carrying several vibration absorbers. Explicit expressions were presented for the generalized orthogonality condition. The obtained generalized orthogonality relation was employed along with the assumed modes method to study the forced vibrational response. The numerical simulations indicated that using the common approach could produce erroneous results. The combination of the exact mode shapes of the loaded beam and the corresponding generalized orthogonality relation is necessary for accurate dynamic modeling of a beam carrying elastically mounted masses with dampers.

Conflict of Interests

The authors declare that there is no conflict of interests regarding the publication of this paper.

Appendix

For the sake of simplicity, the following notations are used:

\begin{matrix} s_{α} = \sin α, c_{α} = \cos α, \\ s h_{β} = \sinh β, c h_{β} = \cosh β, \\ s_{α i} = \sin α (ζ_{i}), c_{α i} = \cos α (ζ_{i}), \\ {s h}_{β i} = \sinh β (ζ_{i}), {c h}_{β i} = \cosh β (ζ_{i}), \\ ϵ = K_{1} γ_{1} - η_{1} . \end{matrix}

(A.1)

The elements of the matrix ℱ are expressed as

\begin{matrix} ℱ_{(41,43 i - i -)} = s_{α i}, ℱ_{(41,42 i - i -)} = c_{α i}, \\ ℱ_{(41,41 i - i -)} = {s h}_{β i}, ℱ_{(41,4 i - i)} = {c h}_{β i}, \\ ℱ_{(41,41 i - i +)} = {- s}_{α i}, ℱ_{(41,42 i - i +)} = {- c}_{α i}, \\ ℱ_{(41,43 i - i +)} = {- s h}_{β i}, ℱ_{(41,44 i - i +)} = {- c h}_{β i}, \\ ℱ_{(443 i, i -)} = {α c}_{α i}, ℱ_{(442 i, i -)} = {- α s}_{α i}, \\ ℱ_{(441 i, i -)} = {β c h}_{β i}, ℱ_{(44 i, i)} = {β s h}_{β i}, \\ ℱ_{(441 i, i +)} = {- α c}_{α i}, ℱ_{(442 i, i +)} = {α s}_{α i}, \\ ℱ_{(443 i, i +)} = {- β c h}_{β i}, ℱ_{(444 i, i +)} = {- β s h}_{β i}, \\ ℱ_{(41,43 i + i -)} = {α^{2} s}_{α i}, ℱ_{(41,42 i + i -)} = {- α^{2} c}_{α i}, \\ ℱ_{(41,41 i + i -)} = {β^{2} s h}_{β i}, ℱ_{(41,4 i + i)} = {β^{2} c h}_{β i}, \\ ℱ_{(41,41 i + i +)} = {α^{2} s}_{α i}, ℱ_{(41,42 i + i +)} = {α^{2} c}_{α i}, \\ ℱ_{(41,43 i + i +)} = {- β^{2} s h}_{β i}, ℱ_{(41,44 i + i +)} = {- β^{2} c h}_{β i}, \\ ℱ_{(42,43 i + i -)} = {- α^{3} c}_{α i} + {ϵ s}_{α i}, ℱ_{(42,42 i + i -)} = {α^{3} s}_{α i} + {ϵ c}_{α i}, \\ ℱ_{(42,41 i + i -)} = {β^{3} c h}_{β i} + {ϵ s h}_{β i}, ℱ_{(42,4 i + i)} = {β^{3} s h}_{β i} + {ϵ c h}_{β i}, \\ ℱ_{(42,41 i + i +)} = {α^{3} c}_{α i}, ℱ_{(42,42 i + i +)} = {- α^{3} s}_{α i}, \\ ℱ_{(42,43 i + i +)} = {- β^{3} c h}_{β i}, ℱ_{(42,44 i + i +)} = {- β^{3} s h}_{β i} . \end{matrix}

(A.2)

ℱ_(1,1), ℱ_(1,2), ℱ_(1,3), ℱ_(1,4), ℱ_(2,1), ℱ_(2,2), ℱ_(2,3), and ℱ_(2,4) depend on the boundary conditions at the origin x = 0. ℱ_(q−1,p+1), ℱ_(q−1,p+2), ℱ_(q−1,p+3), ℱ_(q−1,p+4), ℱ_(q,p+1), ℱ_(q,p+2), ℱ_(q,p+3), and ℱ_(q,p+4) are obtained from the boundary conditions at x = L, where q = 4N + 4 and p = 4N.

The frequency equation for a cantilevered beam with one in-span mass-spring-mass support is obtained by taking the determinant of the following matrix:

\begin{matrix} [\begin{bmatrix} 0 & 1 & 0 & 1 & 0 & 0 & 0 & 0 \\ α & 0 & β & 0 & 0 & 0 & 0 & 0 \\ s_{α 1} & c_{α 1} & {s h}_{β 1} & {c h}_{β 1} & {- s}_{α 1} & {- c}_{α 1} & {- s h}_{β 1} & {- c h}_{β 1} \\ {α c}_{α 1} & {- α s}_{α 1} & {β c h}_{β 1} & {β s h}_{β 1} & {- α c}_{α 1} & {α s}_{α 1} & {- β c h}_{β 1} & {- β s h}_{β 1} \\ {- α^{2} s}_{α 1} & {- α^{2} c}_{α 1} & {β^{2} s h}_{β 1} & {β^{2} c h}_{β 1} & {α^{2} s}_{α 1} & {α^{2} c}_{α 1} & {- β^{2} s h}_{β 1} & {- β^{2} c h}_{β 1} \\ {- α^{3} c}_{α 1} + {ϵ s}_{α 1} & {α^{3} s}_{α 1} + {ϵ c}_{α 1} & {β^{3} c h}_{β 1} + {ϵ s h}_{β 1} & {β^{3} s h}_{β 1} + {ϵ c h}_{β 1} & {α^{3} c}_{α 1} & {- α^{3} s}_{α 1} & {- β^{3} c h}_{β 1} & {- β^{3} s h}_{β 1} \\ 0 & 0 & 0 & 0 & s_{α} & c_{α} & {s h}_{β} & {c h}_{β} \\ 0 & 0 & 0 & 0 & {α c}_{α} & {- α s}_{α} & {β c h}_{β} & {β s h}_{β} \end{bmatrix}] . \end{matrix}

(A.3)

References

1 Lin H.-Y. and Tsai Y.-C., Free vibration analysis of a uniform multi-span beam carrying multiple spring-mass systems, Journal of Sound and Vibration. (2007) 302, no. 3, 442–456, 2-s2.0-33847311733, https://doi.org/10.1016/j.jsv.2006.06.080.
10.1016/j.jsv.2006.06.080
Web of Science® Google Scholar
2 Hassanpour P. A., Cleghorn W. L., Mills J. K., and Esmailzadeh E., Exact solution of the oscillatory behavior under axial force of a beam with a concentrated mass within its interval, Journal of Vibration and Control. (2007) 13, no. 12, 1723–1739, 2-s2.0-36549058234, https://doi.org/10.1177/1077546307076285.
10.1177/1077546307076285
Web of Science® Google Scholar
3 Şakar G., The effect of axial force on the free vibration of an Euler-Bernoulli beam carrying a number of various concentrated elements, Shock and Vibration. (2013) 20, no. 3, 357–367, https://doi.org/10.3233/SAV-120750.
10.3233/SAV-120750
Web of Science® Google Scholar
4 Xiao H., Sheng M., Liu Z., and Wei Z., The study on free vibration of elastically restrained beams carrying various types of attachments with arbitrary spatial distributions, Shock and Vibration. (2013) 20, no. 3, 369–383, https://doi.org/10.1155/2013/983451.
10.3233/SAV-120751
Web of Science® Google Scholar
5 Su H. and Banerjee J. R., Exact natural frequencies of structures consisting of two-part beam-mass systems, Structural Engineering and Mechanics. (2005) 19, no. 5, 551–566, 2-s2.0-18744368789.
10.12989/sem.2005.19.5.551
Web of Science® Google Scholar
6 Saeedi K. and Bhat R. B., Clustered natural frequencies in multi-span beams with constrained characteristic functions, Shock and Vibration. (2011) 18, no. 5, 697–707, 2-s2.0-80052607931, https://doi.org/10.3233/SAV-2010-0592.
10.3233/SAV-2010-0592
Web of Science® Google Scholar
7 Yesilce Y., Free vibrations of a Reddy-Bickford multi-span beam carrying multiple spring-mass systems, Shock and Vibration. (2011) 18, no. 5, 709–726, 2-s2.0-80052628902, https://doi.org/10.3233/SAV-2010-0593.
10.3233/SAV-2010-0593
Web of Science® Google Scholar
8 Chen Y., On the vibration of a beam or rods carrying a concentrated mass, Journal of Applied Mechanics. (1963) 30, no. 2, 310–311, https://doi.org/10.1115/1.3636537.
10.1115/1.3636537
Google Scholar
9 Naguleswaran S., Transverse vibrations of an Euler-Bernoulli uniform beam carrying two particles in-span, International Journal of Mechanical Sciences. (2001) 43, no. 12, 2737–2752, 2-s2.0-0035545765, https://doi.org/10.1016/S0020-7403(01)00072-8.
10.1016/S0020-7403(01)00072-8
Web of Science® Google Scholar
10 Wu J.-S. and Lin T.-L., Free vibration analysis of a uniform cantilever beam with point masses by an analytical-and-numerical-combined method, Journal of Sound and Vibration. (1990) 136, no. 2, 201–213, 2-s2.0-0025254751, https://doi.org/10.1016/0022-460X(90)90851-P.
10.1016/0022-460X(90)90851-P
Web of Science® Google Scholar
11 Gürgöze M., On the alternative formulations of the frequency equation of a Bernoulli-Euler beam to which several spring-mass systems are attached in-span, Journal of Sound and Vibration. (1998) 217, no. 3, 585–595, 2-s2.0-0032179916, https://doi.org/10.1006/jsvi.1998.1796.
10.1006/jsvi.1998.1796
Web of Science® Google Scholar
12 Cha P. D., Natural frequencies of a linear elastica carrying any number of sprung masses, Journal of Sound and Vibration. (2001) 247, no. 1, 185–194, 2-s2.0-0035846035, https://doi.org/10.1006/jsvi.2001.3623.
10.1006/jsvi.2001.3623
Web of Science® Google Scholar
13 Barry O. R., Zu J., Zu J. W., and Oguamanam D. C. D., Free vibration analysis of a beam under axial load carrying a mass-spring-mass system, Proceedings of the ASME International Design Engineering Technical Conferences & Computers and Information in Engineering Conference (IDETC/CIE ′12), August 2012, Chicago, Ill, USA, 791–796, https://doi.org/10.1115/DETC2012-70144.
10.1115/DETC2012-70144
Google Scholar
14 Hamdan M. N. and Jubran B. A., Free and forced vibrations of a restrained cantilever beam carrying a concentrated mass, Journal of Engineering Science. (1991) 3, no. 1, 71–83.
Google Scholar
15 Samani F. S. and Pellicano F., Vibration reduction on beams subjected to moving loads using linear and nonlinear dynamic absorbers, Journal of Sound and Vibration. (2009) 325, no. 4-5, 742–754, 2-s2.0-67649476122, https://doi.org/10.1016/j.jsv.2009.04.011.
10.1016/j.jsv.2009.04.011
Web of Science® Google Scholar
16 Wu J.-S. and Chen D.-W., Dynamic analysis of a uniform cantilever beam carrying a number of elastically mounted point masses with dampers, Journal of Sound and Vibration. (2000) 229, no. 3, 549–578, 2-s2.0-0033749008, https://doi.org/10.1006/jsvi.1999.2504.
10.1006/jsvi.1999.2504
Web of Science® Google Scholar
17 Wu J.-S. and Huang C.-G., Free and forced vibrations of a Timoshenko beam with any number of translational and rotational springs and lumped masses, Communications in Numerical Methods in Engineering. (1995) 11, no. 9, 743–756, https://doi.org/10.1002/cnm.1640110905.
10.1002/cnm.1640110905
Web of Science® Google Scholar
18 Zhang B. and Shepard S., Dynamic response of supported beams with intermediate supports under moving loads, Shock and Vibration. (2012) 19, no. 6, 1403–1413, https://doi.org/10.1155/2012/849298.
10.3233/SAV-2012-0682
Web of Science® Google Scholar
19 Chang T.-P. and Chang C.-Y., Vibration analysis of beams with a two degree-of-freedom spring-mass system, International Journal of Solids and Structures. (1998) 35, no. 5-6, 383–401, 2-s2.0-0031994311, https://doi.org/10.1016/S0020-7683(97)00037-1.
10.1016/S0020-7683(97)00037-1
Web of Science® Google Scholar
20 Low K. H., Comments on “non-linear vibrations of a beam-mass system under different boundary conditions” (with authors′ reply), Journal of Sound and Vibration. (1997) 207, no. 2, 284–287, https://doi.org/10.1006/jsvi.1997.1135.
10.1006/jsvi.1997.1135
Google Scholar
21 Özkaya E. and Pakdemirli M., Non-linear vibrations of a beam-mass system with both ends clamped, Journal of Sound and Vibration. (1999) 221, no. 3, 491–503, 2-s2.0-0000953760, https://doi.org/10.1006/jsvi.1998.2003.
10.1006/jsvi.1998.2003
Web of Science® Google Scholar
22 Ghayesh M. H., Alijani F., and Darabi M. A., An analytical solution for nonlinear dynamics of a viscoelastic beam-heavy mass system, Journal of Mechanical Science and Technology. (2011) 25, no. 8, 1915–1923, 2-s2.0-80052211555, https://doi.org/10.1007/s12206-011-0519-4.
10.1007/s12206-011-0519-4
Web of Science® Google Scholar
23 Ghayesh M. H., Kazemirad S., and Darabi M. A., A general solution procedure for vibrations of systems with cubic nonlinearities and nonlinear/time-dependent internal boundary conditions, Journal of Sound and Vibration. (2011) 330, no. 22, 5382–5400, 2-s2.0-79961000310, https://doi.org/10.1016/j.jsv.2011.06.001.
10.1016/j.jsv.2011.06.001
Web of Science® Google Scholar
24 Kirk C. L. and Wiedemann S. M., Natural frequencies and mode shapes of a free-free beam with large end masses, Journal of Sound and Vibration. (2002) 254, no. 5, 939–949, 2-s2.0-0037173827, https://doi.org/10.1006/jsvi.2001.4138.
10.1006/jsvi.2001.4138
Web of Science® Google Scholar
25 Hassanpour P. A., Esmailzadeh E., Cleghorn W. L., and Mills J. K., Generalized orthogonality condition for beams with intermediate lumped masses subjected to axial force, Journal of Vibration and Control. (2010) 16, no. 5, 665–683, 2-s2.0-77951103933, https://doi.org/10.1177/1077546309106526.
10.1177/1077546309106526
Web of Science® Google Scholar

Citing Literature

All articles

On the Dynamic Analysis of a Beam Carrying Multiple Mass-Spring-Mass-Damper System

Correction(s) for this article

Erratum to “On the Dynamic Analysis of a Beam Carrying Multiple Mass-Spring-Mass-Damper System”

Abstract

1. Introduction

2. Equations of Motion

3. Frequency Equation and Mode Shapes

4. Generalized Orthogonality Relations

5. Forced Vibration

6. Numerical Simulation

7. Conclusions

Conflict of Interests

Appendix

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

On the Dynamic Analysis of a Beam Carrying Multiple Mass-Spring-Mass-Damper System

Correction(s) for this article

Erratum to “On the Dynamic Analysis of a Beam Carrying Multiple Mass-Spring-Mass-Damper System”

Abstract

1. Introduction

2. Equations of Motion

3. Frequency Equation and Mode Shapes

4. Generalized Orthogonality Relations

5. Forced Vibration

6. Numerical Simulation

7. Conclusions

Conflict of Interests

Appendix

References

Citing Literature

Figures

References

Related

Information