Iterative feedback tuning (IFT) is a data-based tuning approach that minimizes a quadratic performance index using some closed-loop experimental data. A control weighting coefficient, known as lambda, and two frequency filters are the most important parameters which can significantly improve the performance of the method. One of the major problems in IFT is tuning these parameters. This paper presents a new approach to tune frequency filters using particle swarm optimization (PSO). At the end, the performance of the proposed method is evaluated by two case study simulations.

1. Introduction

Iterative feedback tuning (IFT) is a data-based method for the tuning of controllers with restricted complexity which was proposed by Hjalmarsson et al. [1] in 1994. In this method, the problem of model bias could be avoided by replacing the information carried by the model with information achieved directly from the system itself. This leads to an iterative method where the controller parameters are successively updated using information from closed-loop experiments with the most recent controller in the loop. IFT has proved to be very effective in practice and is now greatly used in process control [2]. Since 1994 many experiences have been achieved by IFT algorithm and lots of improvements have been observed [3–13].

In order to fully take advantage of IFT, a new scheme needs to be introduced to tune the efficient parameters. In earlier studies, the importance of IFT parameters was confirmed and a few tuning key points were presented [8], but the tuning of these parameters has not been treated in much detail. However, some approaches have been proposed to tune similar parameters. Shridhar and Cooper [14] derived an analytical expression in which the suppression coefficients are calculated as a function of the plant model parameters. Kai et al. [15] proposed a min-max algorithm to design tuning parameters. Al-Ghazzawi et al. [16] presented an approach to tuning MPC on-line based on sensitivity equations derived from a step response model with linear constraints.

The IFT’s parameters are mainly a scalar, named lambda, and two frequency filters. This paper provides a method to tune the frequency filters which can emphasize or suppress specific frequency bands of the output and control signals. These filets affect the IFT’s performance greatly. Therefore, convenient design of these filters seems critical. In order to tune these filters, the particle swarm optimization (PSO) is proposed, which tunes frequency filters using the input-output data achieved from IFT algorithm. This method is proposed for the first order filters with two parameters.

The paper is organized as follows: a brief explanation of IFT algorithm is presented in Section 2. In Section 3, the particle swarm optimization method is briefly described and implemented to tune the frequency filters. Consequently, we shed some light on the performance of the proposed method for tuning the frequency filters, by applying the improved IFT to some case study systems in Section 4. Finally, the paper is concluded in Section 5 with a summary of key points and results.

2. Iterative Feedback Tuning Approach

Consider the SISO closed-loop system as presented in Figure 1. From the figure, it can be followed that

()

where G is an unknown single input-single output (SISO) operator which is linear time invariant (LTI), y(t) is the process output, u(t) is the corresponding process input, and v(t) is an immeasurable disturbance which is assumed to be stochastic. r_t is an external deterministic reference signal which is independent of {v(t)}. C = {C_r(ρ), C_y(ρ)} are linear time invariant transfer functions parameterized by parameter vector ρ.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

SISO closed loop system.

Assuming y^d as a desired output response to the reference signal r, for closed-loop system, the error between the achieved and desired response is

()

The control design objective can be formulated as

()

where E[·] denotes expectation with respect to the disturbance v. Scalar λ is the weighting coefficient expressing the relative importance of the penalty on the control effort, and the symbols L_y and L_u are some frequency filters which can emphasize or suppress specific frequency bands of the output and control signals. These filters can be used for some purposes such as

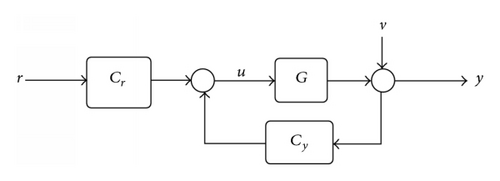
(i)
emphasizing or suppressing specific frequency bands of the outputs and control signals, for instance, to prevent unwanted oscillations in these signals:
(ii)
using as notch filters in the frequency bands where the measurement noise dominates;
(iii)
meeting specific frequency domain performance specifications, such as constraints on the sensitivities.

For minimizing J, IFT estimates the gradient ∂J/∂ρ only using some special closed-loop experiments. The detailed procedure of estimating the gradient can be seen in [8]. After estimating the gradient ∂J/∂ρ, the parameters of the controller are updated by the following iterative algorithm:

()

Here, R_i is an appropriate positive definite matrix which is typically a Gauss-Newton approximation of the Hessian of J while γ_i is a real positive scalar which defines the step size of the algorithm.

3. Particle Swarm Optimization

Particle swarm optimization (PSO) is a population-based optimization approach first proposed in 1995 [17, 18]. This method is urged by the observation of social interaction and animal behaviours such as fish schooling and bird flocking [19–21].

Similar to most optimization techniques, PSO requires a cost function evaluation function relevant to the particle’s position. As L_y and L_u affect the output signal and the input signal, the proposed cost function consists of the integrated absolute error (IAE) defined as follows [22]:

()

And the second part of the cost function is total variation (TV) of the manipulated input. This criterion is used to evaluate the required control effort which is a convenient measure of “smoothness” of control input and should be as small as possible [22]:

()

Thus, the cost function can be defined as

()

All solutions in PSO can be represented as particles in a swarm. Each particle has a position and velocity vector and each position coordinate represents a parameter value. The current position of ith particle of the swarm is denoted by x_i.

and

are the personal best (Pbest) position and global best (Gbest) position of the ith particle. Each particle is initialized with a random position and velocity. The velocity of each particle is accelerated toward the global best and its own personal best based on the following equation:

()

Here r₁ and r₂ are two random numbers generated from a uniform distribution in the range [0,1]; c₁ and c₂ are the acceleration constants and w is the inertia weight factor. Suitable selection of these parameters provides a balance between global and local explorations and helps the particles converge to Gbest. In this paper, the constricted version of PSO [23] is used which sets the parameters as follows:

()

where ϕ₁ = ϕ₂ = 2.05, ϕ = ϕ₁ + ϕ₂.

The positions are updated based on their movement over a discrete time interval (Δt) as follows:

()

where Δt usually is set to 1. Then the cost function at each position is reevaluated to update Gbest and Pbest.

In this paper, the frequency filters are considered as the first order filter as follows:

()

Therefore, the proposed PSO is employed to tune four parameters K₁, T₁, K₂, and T₂. In each iteration of PSO, the IFT algorithm obtains the optimal control parameter with the current filters parameters. Using the updated controller parameters, cost function (7) is changed and it leads to different parameters of frequency filters achieved in PSO algorithm.

4. Simulation Study

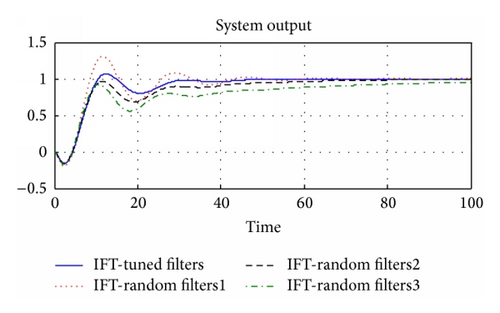
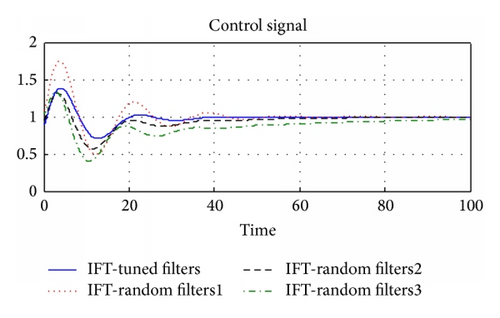
Example 1. A gas boiler system is considered where the gas valve position V₂ is used to control the temperature T of the water. The following transfer function is used to represent the relationship between the variations in V₂ and T when the flow of water is constant [24]:

()

This system is controlled by a PI controller tuned by IFT algorithm. The frequency filters tuned by the proposed PSO method are as follows:

()

The simulation results in Figure 2 and Table 1 indicate that the IFT algorithm tuned by the proposed method gives an acceptable response which can substitute the trial-and-error tuning of the filters. As mentioned before, the frequency filters play a significant role in IFT performance. By many simulations it was observed that IFT is very sensitive to filters parameters. By a random selection of the filters parameters, it was observed that poorly tuned filters can lead to unstable responses. To show the filters effect on the responses, the filters parameters are obtained randomly around the optimal values by a 30% tolerance. From Figure 2 and Table 1, it can be seen that small variations of filters parameters can lead to large changes in output response.

Table 1. Controller setting for Example 1 (evaluating the proposed frequency filters effect).

Tuning method	K₁	T₁	K₂	T₂	S. T.	Os%	IAE	TV
Tuned filters	0.507	0.127	0.094	3.071	43.63	6.68	101.37	1.59
Random filters 1	0.71	0.14	0.06	3.22	41.89	29.8	114.65	3.24
Random filters 2	0.59	0.12	0.13	2.93	69.32	0	139.5	1.69
Random filters 3	0.53	0.15	0.1	2.14	125	0	2.08	2.05

S. T.: Settling time.

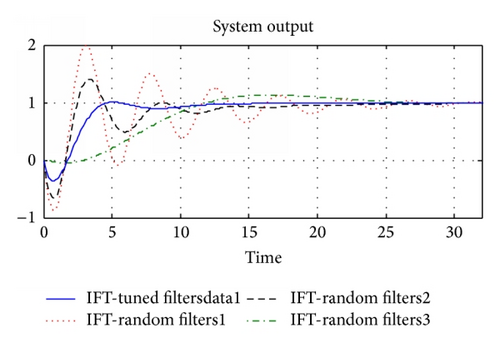
Example 2. Consider the control system of a heated tank. The dynamics relating the control action and the temperature can be modelled with an FOPDT model as follows [24]:

()

The output response and control signal of the system are depicted in Figure 3 in which the IFT tuned by the proposed method has been compared to IFT with the randomly tuned filters. Here, more freedom was assigned to select the random filters. Therefore, the effect of these filters has been shown better. The simulation results can be seen in Table 2.

Table 2. Controller setting for Example 2 (evaluating the proposed frequency filters effect).

Tuning method	K₁	T₁	K₂	T₂	S. T.	Os%	IAE	TV
Tuned filters	2.321	0.91	1.1	4.52	13.021	0.458	39.21	39.33
Random filters 1	2	0.22	1.7	2.1	33.71	98.81	96.43	5.19
Random filters 2	3.16	0.22	2.2	1.9	23.88	40.33	58.84	1.66
Random filters 3	3	0.15	1	0.83	24.75	13.098	86.81	0.3439

S. T.: Settling time.

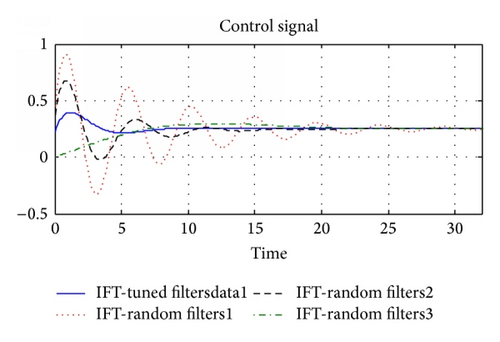
5. Conclusion

The earlier attempts to tune the frequency filters were based on trial-and-error. In this study, these filters were designed using the PSO method. The proposed method was applied to a case study system. It was observed that the performance of IFT modified by the proposed methods was greatly improved. Therefore, IFT has become more capable with a better performance. The proposed method for designing frequency filters in this study is not merely limited to IFT algorithm; therefore, future studies are recommended to generalize the proposed approach to other methods with similar parameters. Also, a further study with focus on high order filters is suggested.

Conflict of Interests

The author declares that there is no conflict of interests regarding the publication of this paper.

References

1 Hjalmarsson H., Gunnarsson S., and Gevers M., Convergent iterative restricted complexity control design scheme, Proceedings of the 33rd IEEE Conference on Decision and Control, December 1994, Orlando, Fla, USA, IEEE, 1735–1740, 2-s2.0-0028748855.
Google Scholar
2 Hjalmarsson H., Iterative feedback tuning—an overview, International Journal of Adaptive Control and Signal Processing. (2002) 16, no. 5, 373–395, https://doi.org/10.1002/acs.714, 2-s2.0-0036608321.
Google Scholar
3 Huusom J. K., Poulsen N. K., and Jørgensen S. B., Improving convergence of iterative feedback tuning, Journal of Process Control. (2009) 19, no. 4, 570–578, https://doi.org/10.1016/j.jprocont.2008.09.004, 2-s2.0-63249126041.
Google Scholar
4 Huusom J. K., Hjalmarsson H., Poulsen N. K., and Jorgensen S. B., A design algorithm using external perturbation to improve iterative feedback tuning convergence, Automatica. (2011) 47, no. 12, 2665–2670, https://doi.org/10.1016/j.automatica.2011.05.029, MR2886935, 2-s2.0-81155123058.
Google Scholar
5 Hjalmarsson H., Efficient tuning of linear multivariable controllers using iterative feedback tuning, International Journal of Adaptive Control and Signal Processing. (1999) 13, no. 7, 553–572, https://doi.org/10.1002/(SICI)1099-1115(199911)13:7<553::AID-ACS572>3.0.CO;2-B, MR1822604, ZBL0947.93026.
Google Scholar
6 Ho W. K., Hong Y., Hansson A., Hjalmarsson H., and Deng J. W., Relay auto-tuning of PID controllers using iterative feedback tuning, Automatica. (2003) 39, no. 1, 149–157, https://doi.org/10.1016/S0005-1098(02)00201-7, MR2136563, 2-s2.0-0037211172.
Google Scholar
7 Tsang K., Rad A. B., and Chan W., Iterative feedback tuning for positive feedback time delay controller, International Journal of Control, Automation and Systems. (2005) 3, no. 4, 640–645, 2-s2.0-28844444888.
Google Scholar
8 Hjalmarsson H., Gevers M., Gunnarsson S., and Lequin O., Iterative feedback tuning: theory and applications, IEEE Control Systems Magazine. (1998) 18, no. 4, 26–41, https://doi.org/10.1109/37.710876, 2-s2.0-0032140408.
Google Scholar
9 Graham A. E., Young A. J., and Xie S. Q., Rapid tuning of controllers by IFT for profile cutting machines, Mechatronics. (2007) 17, no. 2-3, 121–128, https://doi.org/10.1016/j.mechatronics.2006.08.002, 2-s2.0-33846672424.
Google Scholar
10 Kissling S., Blanc P., Myszkorowski P., and Vaclavik I., Application of iterative feedback tuning (IFT) to speed and position control of a servo drive, Control Engineering Practice. (2009) 17, no. 7, 834–840, https://doi.org/10.1016/j.conengprac.2009.02.005, 2-s2.0-67349210675.
Google Scholar
11 Rupp D. and Guzzella L., Iterative tuning of internal model controllers with application to air/fuel ratio control, IEEE Transactions on Control Systems Technology. (2010) 18, no. 1, 177–184, https://doi.org/10.1109/TCST.2008.2010458, 2-s2.0-73249142318.
Google Scholar
12 Liu D., McDaid A. J., Aw K. C., and Xie S. Q., Position control of an Ionic Polymer Metal Composite actuated rotary joint using Iterative Feedback Tuning, Mechatronics. (2011) 21, no. 1, 315–328, https://doi.org/10.1016/j.mechatronics.2010.12.001, 2-s2.0-79551489160.
Google Scholar
13 McDaid A. J., Aw K. C., Haemmerle E., and Xie S. Q., Control of IPMC actuators for microfluidics with adaptive “online” iterative feedback tuning, IEEE/ASME Transactions on Mechatronics. (2012) 17, no. 4, 789–797, https://doi.org/10.1109/TMECH.2011.2135373, 2-s2.0-84860886518.
Google Scholar
14 Shridhar R. and Cooper D. J., A novel tuning strategy for multivariable model predictive control, ISA Transactions. (1997) 36, no. 4, 273–280, https://doi.org/10.1016/S0019-0578(97)00036-0, 2-s2.0-0031376713.
Google Scholar
15 Kai H., Jun Z., and Jixin Q., A novel robust tuning strategy for model predictive control, Proceedings of the 6th World Congress on Intelligent Control and Automation (WCICA ′06), June 2006, Dalian, China, 6406–6410, https://doi.org/10.1109/WCICA.2006.1714318, 2-s2.0-34047221498.
Google Scholar
16 Al-Ghazzawi A., Ali E., Nouh A., and Zafiriou E., On-line tuning strategy for model predictive controllers, Journal of Process Control. (2001) 11, no. 3, 265–284, https://doi.org/10.1016/S0959-1524(00)00033-0, 2-s2.0-0035372308.
Google Scholar
17 Kennedy J. and Eberhart R., Particle swarm optimization, Proceedings of the IEEE International Conference on Neural Networks, December 1995, Perth, Australia, IEEE Service Centre, 1942–1948, 2-s2.0-0029535737.
Google Scholar
18 Eberhart R. C. and Kennedy J., A new optimizer using particles swarm theory, Proceedings of the 6th International Symposium on Micro Machine and Human Science, 1995, Nagoya, Japan, IEEE Service Center, 39–43.
Google Scholar
19 BartzBeielstein T., Parsopoulos K. E., and Vrahatis M. N., Analysis of particle swarm optimization using computational statistics, Proceedings of the International Conference on Numerical Analysis and Applied Mathematics (ICNAAM ′04), 2004, 34–37.
Google Scholar
20 Zhao J., Li T., and Qian J., Application of particle swarm optimization algorithm on robust PID controller tuning, Proceedings of the 1st International Conference on Natural Computation (ICNC ′05), August 2005, Berlin, Germany, Springer, 948–957, 2-s2.0-26844491002.
Google Scholar
21 Hu H., Hu Q., Lu Z., and Xu D., Optimal PID controller design in PMSM servo system via particle swarm optimization, Proceedings of the 31st Annual Conference of IEEE Industrial Electronics Society, November 2005, 79–83, https://doi.org/10.1109/IECON.2005.1568882, 2-s2.0-33749661408.
Google Scholar
22 Chen D. and Seborg D. E., PI/PID controller design based on direct synthesis and disturbance rejection, Industrial and Engineering Chemistry Research. (2002) 41, no. 19, 4807–4822, https://doi.org/10.1021/ie010756m, 2-s2.0-0037130751.
Google Scholar
23 Clerc M. and Kennedy J., The particle swarm-explosion, stability, and convergence in a multidimensional complex space, IEEE Transactions on Evolutionary Computation. (2002) 6, no. 1, 58–73, https://doi.org/10.1109/4235.985692, 2-s2.0-0036464756.
Web of Science® Google Scholar
24 Normey-Rico J. E. and Camacho E. F., Control of Dead-Time Processe, 2007, Springer, New York, NY, USA.
Google Scholar

Citing Literature

All articles

The Design of Frequency Filters of Iterative Feedback Tuning Using Particle Swarm Optimization

Abstract

1. Introduction

2. Iterative Feedback Tuning Approach

3. Particle Swarm Optimization

4. Simulation Study

5. Conclusion

Conflict of Interests

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

The Design of Frequency Filters of Iterative Feedback Tuning Using Particle Swarm Optimization

Abstract

1. Introduction

2. Iterative Feedback Tuning Approach

3. Particle Swarm Optimization

4. Simulation Study

5. Conclusion

Conflict of Interests

References

Citing Literature

Figures

References

Related

Information