On Finite-Time Feedback Control for Switched Discrete-Time Systems under Fast and Slow Switching
Abstract
The problem of finite-time stabilization for switched discrete-time systems under both fast and slow switching is addressed. In the fast switching case, the designed static state feedback controller combines controllers for each subsystem and resetting controller at switching instant, it is shown that the resetting controller can reduce the conservativeness on controller design. Then the results are extended to output feedback controller design. Under slow switching, both static state feedback and output feedback controller are designed with admissible average dwell time, respectively. Several numerical examples are given to illustrate the proposed results within this paper.
1. Introduction
A switched system consists of a finite number of subsystems that are switched according to the time variation of the system’s mode of operation. Many physical processes possess switched and hybrid nature [1–3], and switched systems arise in many engineering applications, for example, in motor engine control [4], constrained robotics [5], and networked control systems [6]. Due to their ubiquity in modern engineering problems, switched systems are receiving increasing interest and attention as the recent books [1, 2] and survey articles [3, 7, 8] indicate. Stability and stabilization are the main concerns in the field of switched systems. Many Lyapunov function techniques are effective tools dealing with switched systems [9–11]. Dwell time and average dwell time approaches were employed to study the stability and stabilization of time-dependent switched systems [12–14].
On the other hand, the finite-time stability is a concept dealing with the boundness of system during a fixed finite-time interval, which mainly focuses on admitting the state does not exceed a certain bound during a fixed finite-time interval, for instance, to avoid saturations or the excitation of nonlinear dynamics. A distinction should be made between classical Lyapunov stability and finite-time stability (or short-time stability). The concept of Lyapunov asymptotic stability is largely known to the control community; conversely a system is said to be finite-time stable if, once we fix a time interval, its state does not exceed some bounds during this time interval. Often asymptotic stability is enough for practical applications, but there are some cases where large values of the state are not acceptable, for instance, in the presence of saturations. In these cases, we need to check that these unacceptable values are not attained by the state; for these purposes finite-time stability could be used. Some early results about finite-time stability can be found in [15–17]. More recently, [18] investigated the output feedback finite-time stabilization for continuous linear system. Finite-time stability and stabilization for discrete linear system were investigated in [19]. Moreover, the robust finite-time control for linear switched discrete-time system with norm-bounded disturbance was considered in [20], and continuous-time case is considered in [21].
Similar as indicated for asymptotic stability, the finite-time stability is supposed to be affected significantly by switching among several subsystems [20, 21]. Thus, besides Lyapunov asymptotic stability, another important system property we are interested in is the boundness of the state during the short time interval in which the switching occurs, and it is explicit that the boundness of state during the short time interval could be influenced significantly by the switching. To avoid the state reaching the unacceptable large values caused by switching during the short time interval, the boundness property of state, that is, the finite-time stability, needs to be considered when we design the controller and switching law. However, most of the existing stability results were about Lyapunov stability; few results have been reported in literature about the finite-time stability of switched systems so far. This motivates the present study.
In this paper, solutions for finding state and output feedback controller guaranteeing the finite-time stabilization of switched discrete-time system are given in both fast switching and slow switching case. In fast switching case, a natural idea is to find a single common positive matrix satisfying finite-time stabilization condition for each subsystem to ensure the finite-time stability of closed-loop switched system which is similar to the common Lyapunov function approach dealing with asymptotic stability. However, it often yields overly conservativeness. To reduce the conservativeness our approach is based on searching for a set of positive matrices; furthermore it is worth noting that the controller combines the controller for each subsystem and resetting controller at switching instant which generates a proper state impulsive jumping which could further reduce the conservativeness in finite-time controller design. In slow switching case, the controller design is proposed including the controllers for subsystems and the admissible average dwell time. The results in fast and slow switching case are both extended to output feedback case. Several numerical simulations are proposed to show the effectiveness of our approach.
The rest of this paper is organized as follows. In Section 2 the problem formulation and some preliminaries are introduced. The main results, finite-time stabilization under fast switching and slow switching, are given in Sections 3 and 4, respectively; several numerical simulations are given to illustrate our proposed results. Conclusions are given in Section 5.
Notations. The notations used in this paper are fairly standard. The superscript “T” stands for matrix transposition, denotes the n-dimensional Euclidean space and represents the set of nonnegative integers, and the notation ‖·‖ refers to the Euclidean norm. In addition, in symmetric block matrices, we use * as an ellipsis for the terms that are introduced by symmetry and diag{⋯} stands for a block-diagonal matrix. λmin(P) and λmax(P) stand for the smallest and the largest eigenvalue of matrix P. The notation P > 0 (P ≥ 0) means P is real symmetric and positive definite (semipositive definite).
2. Preliminaries
For switched discrete-time system, the general conception of finite-time stability concerns the boundness of discrete state x(k) over finite discrete-time interval [0, M], with respect to given initial condition x0. This conception can be formulized through following definition.
Definition 1 (finite-time stability). Switched system
Then we recall the following lemma, which will be used in the proof of our main results.
Lemma 2 is the well-known Schur complement lemma.
3. Finite-Time Stabilization under Fast Switching
Remark 3. From (5a) and (5b) we see that the state impulsive jumping idea is applied since the state feedback controller combines controllers for each subsystem and resetting controller generating a proper state impulsive jumping at switching instant.
Before deriving the conditions for finite-time stabilization of switched system ((1a), (1b)), some explicit facts are recalled. For a symmetric positive definite matrix , it is easy to verify that R can be factorized according to R = (R1/2) TR1/2, where is a symmetric positive definite matrix. And for any positive definite matrix , there always exist which is positive definite. We present our first result on controller design ensuring the closed-loop system ((5a), (5b)) finite-time stable by following theorem.
Theorem 4. The closed-loop switched system ((5a), (5b)) is finite-time stable with respect to (δ, ε, R, M), if there exist a set of matrices Si, , Xi,j, , and positive scalars α > 0, β > 0, and γ ≥ 1 such that the following conditions are satisfied :
Proof. Let Ki,i = Ki and Substituting Xi,j = Ki,jSi, into (6a); we get
On the other hand we have
It is worth mentioning that the class of switching signal is not specified during above discussion; thus Theorem 4 supplies us with a sufficient condition for finite-time stability of switched system ((5a), (5b)) under arbitrarily fast switching. We note that the result in Theorem 4 depends on the parameter γ. For a fixed γ, conditions (6a), (6b), and (6c) can be expressed in an LMI form. Obviously, in order to find a suitable γ, a one parameter search may be necessary; nevertheless this does not represent a hard computational problem.
Remark 5. Once the state bound ε is not ascertained, a set of optimized controller gains and with minimum value εmin is of interest. Since from (6c) we have ε2 > βγMδ2/α, the minimum value εmin can be found by solving optimization problem minβγMδ2/α subject to (6a) and (6b). Furthermore, when δ is fixed and letting α = 1, β = κα be derived through optimization procedure according to
When we let Ki,j = Ki, , the following design results can be derived.
Corollary 6. The closed-loop switched system ((5a), (5b)) is finite-time stable with respect to (δ, ε, R, M), if there exist a set of matrices Si, Xi, , and positive scalars α > 0, β > 0, and γ ≥ 1 such that the following conditions are satisfied :
Furthermore, if we chose S = Si, , then we get the following results based on search for a single positive matrix.
Corollary 7. The closed-loop switched system ((5a), (5b)) is finite-time stable with respect to (δ, ε, R, M), if there exist a set of matrices S, Xi, , and positive scalars α > 0, β > 0, and γ ≥ 1 such that the following conditions are satisfied :
Obviously, the results in both Theorem 4 and Corollary 6 are based on searching for a set of positive matrices, which would be explicitly less conservative than that based on searching for a common positive matrix in Corollary 7. Moreover, the main advantage of Theorem 4 is that the controller for switched system ((1a), (1b)) designs a reset controller at switching instant, which could reduce the conservativeness compared to Corollary 6 only considering controller for each subsystem. To compare the conservativeness of the above proposed results, a numerical simulation is given in following example.
Example 8. Consider a second order switched system with two subsystems given by
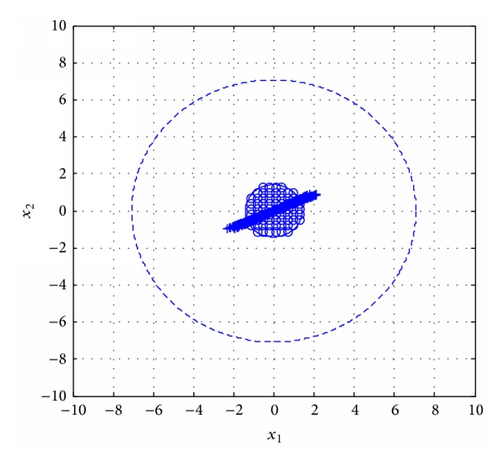
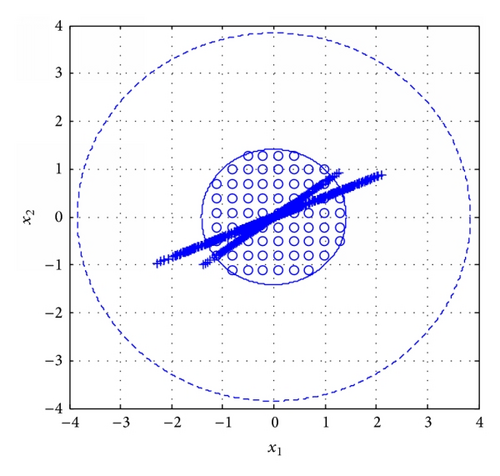
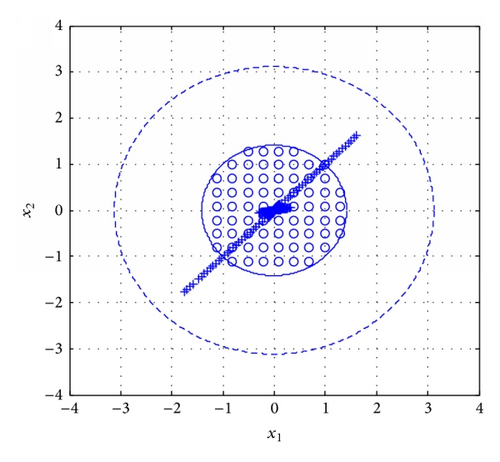
(1) Firstly we design controller based on searching for a single positive matrix by Corollary 7; the controllers are
(2) Then we propose the simulation results by Corollary 6 based on searching for a set of positive matrices but without resetting controller. In this case, we only design controller for each subsystem. The controllers are
(3) Finally we use the proposed approach by Theorem 4 based on searching for a set of positive matrices and with resetting controller. According to Theorem 4, the controllers are given by
Comparing three simulation results in this example, we can see that the conservativeness can be reduced by searching for a set of positive matrices and further considering the resetting controller design.
Then we consider the static output feedback controller u(k) = Kiy(k), , and u(k) = Ki,jy(k), and i ≠ j, ; the closed-loop switched system becomes
Assumption 9. Matrices Ci, , are full of row rank.
Similar to state feedback controller design and based on Assumption 9, the following result can be derived.
Theorem 10. The closed-loop switched system ((30a), (30b)) under Assumption 9 is finite-time stable with respect to (δ, ε, R, M), if there exist a set of matrices Si, , Xi,j, , and positive scalars α > 0, β > 0, and γ ≥ 1 such that the following conditions are satisfied :
Proof. From (31a) we know that Si, , are positive matrices, and Ci, , are full of row rank by Assumption 9; it follows that Yi, , is full of rank and invertible. Thus by (31d), letting Ki,i = Ki and substituting Xi,j = Ki,jYi we obtain
Remark 11. As what is discussed in Remark 3, a set of optimized controller gains and with the minimum εmin can be derived through similar optimization procedure according to
4. Finite-Time Stabilization under Slow Switching
In this section, the finite-time stabilization under slow switching is considered. Now we consider a class of average dwell time switching; the definition of average dwell time is given as follows.
Definition 12 (see [13].)For switched system ((1a), (1b)) and any k2 > k1 ≥ 0, let N(k1, k2) be the number of switchings in the interval [k1, k2). If for any given positive numbers N0 ≥ 0 and τa > 0 we have N(k2, k1) ≤ N0 + (k2 − k1)/τa, then τa and N0 are called average dwell time and chatter bound.
Theorem 13. The closed-loop switched system (40) is finite-time stable with respect to (δ, ε, R, M), if there exist a set of matrices Si, Xi, , and positive scalars α > 0, β > 0, and γ ≥ 1 such that the following conditions are satisfied
Proof. Substituting Xi = KiSi, , into (41a) we get
Example 14. Consider switched system with 2 subsystems as follows:
We chose ; by Theorem 13 the state feedback controller is designed as
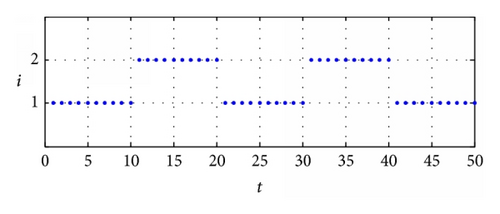
The simulation result is in Figure 5.
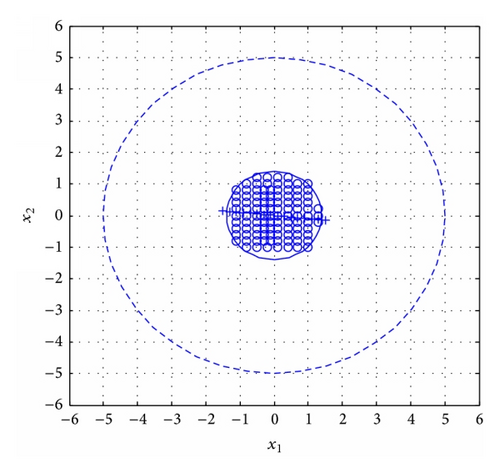
It is explicit that the controller and the switching law with the admissible average dwell time meet requirement of finite-time stabilization.
Theorem 15. The closed-loop switched system (61) under Assumption 9 is finite-time stable with respect to (δ, ε, R, M), if there exist a set of matrices Si, Xi, , and positive scalars α > 0, β > 0, and γ ≥ 1 such that the following conditions are satisfied:
Proof. From the similar guideline in Theorem 10, let , we have
5. Conclusions
The problem of finite-time stabilization for switched discrete-time system is investigated in this paper. Combining the controllers for subsystems and resetting controller at switching instant, the state and output feedback controllers are designed under fast switching. The controller can be obtained by solving a set of LMIs. Then under slow switching, the state and output feedback controllers for subsystems are designed with admissible average dwell time. Several numerical simulations are given to illustrate our approach in this paper.
Conflict of Interests
The authors (Liaoliang Xiao and Mingyang Yu) declare that there is no conflict of interests regarding the publication of this paper.
Acknowledgment
This work is supported by Hunan Provincial Education Department (no. 13C592).




