Discrete Dynamics in Nature and Society
Volume 2014, Issue 1 428568
Research Article
Open Access

Analysis of Price Stackelberg Duopoly Game with Bounded Rationality

Lian Shi, 

Lian Shi

School of Economics and Management, Tongji University, Shanghai 200092, China tongji.edu.cn

Search for more papers by this author
Yun Le, 

Corresponding Author

Yun Le

School of Economics and Management, Tongji University, Shanghai 200092, China tongji.edu.cn

Search for more papers by this author
Zhaohan Sheng, 

Zhaohan Sheng

School of Economics and Management, Tongji University, Shanghai 200092, China tongji.edu.cn

School of Management Science and Engineering, Nanjing University, Nanjing 210093, China nju.edu.cn

Search for more papers by this author
First published: 17 February 2014
https://doi.org/10.1155/2014/428568
Citations: 9
Academic Editor: Stepan A. Tersian

Abstract

The classical Stackelberg game is extended to boundedly rational price Stackelberg game, and the dynamic duopoly game model is described in detail. By using the theory of bifurcation of dynamical systems, the existence and stability of the equilibrium points of this model are studied. And some comparisons with Bertrand game with bounded rationality are also performed. Stable region, bifurcation diagram, The Largest Lyapunov exponent, strange attractor, and sensitive dependence on initial conditions are used to show complex dynamic behavior. The results of theoretical and numerical analysis show that the stability of the price Stackelberg duopoly game with boundedly rational players is only relevant to the speed of price adjustment of the leader and not relevant to the follower’s. This is different from the classical Cournot and Bertrand duopoly game with bounded rationality. And the speed of price adjustment of the boundedly rational leader has a destabilizing effect on this model.

1. Introduction

In the oligopolistic market, oligopoly firms compete in quantity or price. We all know that Cournot model [1] is one of the most famous quantity game models, in which all firms (players) are provided with naive expectations. Presently, boundedly rational quantity oligopoly game has been studied widely, and a player can choose his expectation rule from three different expectations: naive, bounded rational, and adaptive [2, 3]. Many duopoly quantity games with homogeneous or heterogeneous players have been studied under linear or nonlinear demand function and linear or nonlinear cost functions [2–7]. Similarly, some researchers have studied all sorts of triopoly quantity game models [8–13]. These studies find that there are some complex dynamic behaviors such as bifurcation and chaos in the oligopoly quantity game model.

Compared with quantity competition, maybe price competition is more general in a real market. One of the most classical price game models is the Bertrand model [14]. In Bertrand model, each firm will try to reduce its product price, until its products are selling at no profit. This result is called Bertrand paradox. However, the Bertrand paradox rarely appears in practice. One of the reasons is that completely homogeneous product is almost nonexistent. So, one way of avoiding the paradox is to allow the firms to sell differentiated products [15]. Similar to quantity competition, boundedly rational duopoly and triopoly price game models with differentiated products have been studied in [16–19].

In the above mentioned quantity and price game models, the one-short games are static; that is, each of the players in the game determines their quantity or price at the same time. However, dynamic game or sequential game is very common in the real market. We all know that the most classical sequential game is Stackelberg game [20, 21] in which one firm, the leader, commits to a strategy first and publicly, and then the remaining firms, the followers, observe the leader’s choice and make their decisions. The original Stackelberg game model is a quantity game with homogeneous product. Later, it was extended to the differentiated products for both quantity and price game. Vives [22] summarized the literature about the Stackelberg game model and pointed out that the relevant literature took the quantity for decision variable mostly. Until now there is little literature on price Stackelberg game. Consequently, there is no result for boundedly rational price Stackelberg in a differentiated products market. And its dynamic has not been studied. This paper aims to fill this gap.

This paper is organized as follows. In Section 2, the price Stackelberg duopoly game model with boundedly rational players is briefly described. The local stability condition of the equilibrium point is discussed in Section 3. In Section 4, numerical simulations are used to demonstrate the complex dynamics of our model. Finally, the conclusion of this paper is provided in Section 5.

2. The Model

We consider an oligopoly market served by two firms producing differentiated products. The two firms compete in price. Firm 1, as the leader, chooses a price p1 first, and firm 2, as the follower, observes p1 then chooses a price p2. Let pi(n) denote the price of ith firm, i = 1,2 during period n = 0,1, 2, …. The quantity each firm sells Qi, a linear inverse demand function, is determined by the following equations [15, 21]:
()
where a > 0, b > 0, d > 0, and b > d. The parameter d reflects the extent to which the two differentiated products are substitutes for each other. The cost function has the linear form:
()
where ci is the marginal cost of ith firm, so ci is a positive constant.
At the second stage of the period t, firm 2 observes p1(n) then chooses a price p2(n) to maximize its own profits. Thus, the profit of the follower is given by
()
The marginal profit of the firm 2 is
()
Setting ∂Π2(n)/∂p2(n) = 0, the profit-maximizing price for firm 2 is obtained as follow:
()
At the first stage of the period n, the leader’s profit is given by
()
Since firm 1 predicts that firm 2 chooses its optimum price p2(n) in terms of (5), then substituting (5) into (6), we get
()
So, the marginal profit of the firm 1 is
()

In this work, the two firms (leader and follower) are boundedly rational players. They have no complete information of market, and they determine the price of production with the information of local profit maximization.

The leader determines its price of production of period n + 1 on the basis of expected marginal profit ∂Π1(n)/∂p1(n). The leader will increase (decrease) its price for period n + 1 if the marginal profit is positive (negative) at period n. This adjustment mechanism has been called myopic by Dixit in [23]. Thus, this dynamical mechanism can be modeled as
()
where α1 is a positive parameter and represents the speed of adjustment of the leader. Substituting (8) into (9), the dynamical adjustment mechanism of the leader (firm 1) has the following form:
()
The follower is also a boundedly rational player and changes its price according to its marginal profit ∂Π2/∂p2. But, based on the above definition, the follower has known the current production price of the leader when it chooses its production. Hence, it is unreasonable if the follower determines its production price of period n + 1 on the basis of marginal profit of period n(∂Π2(n)/∂p2(n)). In this work, we assume the follower decides the p2(n + 1) according to a forecasting marginal profit of current period. We define it as . By using (4), we have
()
Then the dynamical equation of the follower can be modeled as
()
where α2 is also a positive parameter and represents the adjustment speed of the follower.
Substituting (11) into (12), we have
()
By solving (13), it can be reduced to
()
Thus, the price Stackelberg duopoly game with boundedly rational players is described by the following two-dimensional discrete dynamical system:
()

One can see that the form of this dynamical system is so different from the previous classical Cournot and Bertrand duopoly game with bounded rationality. And the product price of the leader at period n + 1 is only relevant to its own price of period n; but the product price of the follower at period n + 1 is determined by its own price of period n and the leader’s price of period n + 1. In addition, this model is unsymmetrical and this is different from the Zhang’s [16] and Peng’s model, [19], in which their models are symmetrical. Maybe these will give rise to different result and complicated dynamics from the boundedly rational Cournot and Bertrand duopoly game.

3. Equilibrium Points and Local Stability

We are interested only in nonnegative trajectories; hence, the system is not defined in the origin (0,0). By setting pi(n + 1) = pi(n) = pi in the dynamical system (15), we get the following nonlinear algebraic system:
()
It is easy to work out two fixed points:
()
where
()
Obviously, E1 is a boundary equilibrium. The fixed point E* is the Nash equilibrium and has economic sense due to b > d.
Easily, we can get the following:
()
For comparison, setting c1 = c2 = c, then we have
()
The quantity Q1 = Q2 = a − bc + cd > 0 when price p1 = p2 = c, so . That is to say, in Nash equilibrium the leader’s product price is always greater than follower’s product price.
In addition, we remember that in Zhang’s model [16] the product price of firm 1 in the Nash equilibrium is
()
Obviously, of our model is less than of Zhang’s model. (This is comparable because there are the same inverse demand functions and linear cost functions in our model and Zhang’s model.) This is beneficial for consumers.
In order to investigate the local stability of the equilibrium points of E1 and E*, we return to the two-dimensional dynamical system. Let J be the Jacobian matrix of the system corresponding to the state variables (q1,,  q2) then
()
where
()
The stability of equilibrium points will be determined by the nature of the eigenvalues of the Jacobian matrix evaluated at the corresponding equilibrium points.

Theorem 1. The boundary equilibrium point E1 of the system (15) is unstable.

Proof. The Jacobian matrix at E1 takes the form:

()
Its eigenvalues are
()
Since a > 0, b > 0, ci > 0  (i = 1,2) and b > d, so we have that |λ1| < 1 and |λ2| > 1. Then E1 is a saddle point of discrete dynamical system (15). This completes the proof of the Theorem 1.

Next, we will investigate the local stability of the Nash equilibrium point E*.

3.1. Local Stability of Nash Equilibrium Point E*

The Jacobian matrix at E* takes the form:
()
Its eigenvalues are
()
If the eigenvalues λi,  i = 1,2, satisfy inequalities |λi| < 1,  i = 1,2, then the Nash equilibrium points will be locally stable. First, |λi| < 1 that is
()
It can be reduced to
()
Substituting , we have
()
Then |λ2| < 1 equal to . This inequality is always fulfilled due to α2, b, and .

So, we can state the following summarizing result.

Theorem 2. The Nash equilibrium E* of the dynamical system (15) is locally asymptotically stable provided that

()
The inequality (31) defines a range in which the Nash equilibrium point E* is stable; otherwise the Nash equilibrium point E* loses its stability through the boundary of this range. And one can conclude that the stability of the dynamical system (15) is only relevant to the adjustment speed of the leader and not relevant to the follower’s adjustment speed. This result is significant and different from the classical Cournot and Bertrand duopoly game with bounded rationality. In addition, one can see, stability region of the Nash equilibrium point is a decreasing function with respect to the market capacity a and the marginal cost c1.

These inferences will be demonstrated in Section 4.

4. Numerical Simulations

In order to be more clear and intuitive in understanding the complex dynamic behavior of the discrete dynamical system (15), numerical analysis is used to describe the dynamical evolution process. For convenience, we take a = 2, b = 0.5, c1 = 0.2, c2 = 0.4, d = 0.3 to study the local stability properties of the Nash equilibrium point. By calculation, we get the Nash equilibrium E* = (3.3439,  3.2032).

Figure 1 shows the price bifurcation diagram with respect to α1 (the adjustment speed of boundedly rational leader) of dynamical system (15) when α2 = 0.5. One can see the Nash equilibrium E* = (3.3439,  3.2032) is locally stable when the parameter α1 is small. As α1 increases, the Nash equilibrium point becomes unstable; that is, Period-2 and period-4 bifurcations appear and finally chaotic scenario occur. Definitely, when α1 > 0.7294, flip (period-doubling) bifurcation occurs and complex dynamic behavior begins to appear. Obviously, this fluctuation of system is harmful to both firms. One can conclude that the speed of adjustment of the boundedly rational leader α1 has a destabilizing effect to the dynamical system (15). The Largest Lyapunov exponent which corresponds to Figure 1 is plotted in Figure 2. This diagram also shows the relationship between the local stability of the Nash equilibrium point and the speed of adjustment of the boundedly rational leader α1. And one can obtain a better understanding of dynamical behaviors of the system (15).

Details are in the caption following the image
Figure 1
Open in figure viewerPowerPoint
Bifurcation diagram with respect to α1 when α2 = 0.5.
Details are in the caption following the image
Figure 2
Open in figure viewerPowerPoint
The largest Lyapunov exponent versus α1 ∈ [0,1.06] for α2 = 0.5.

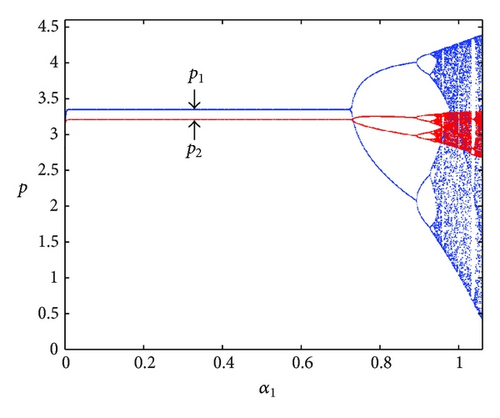
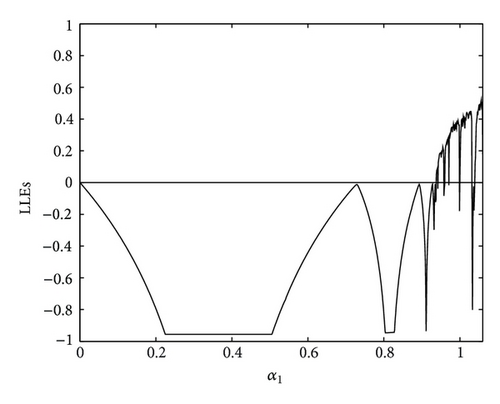
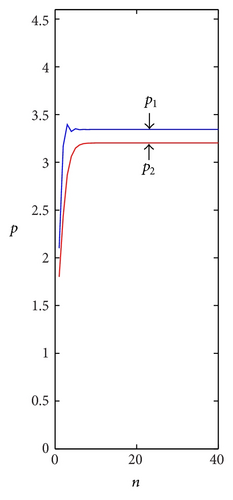
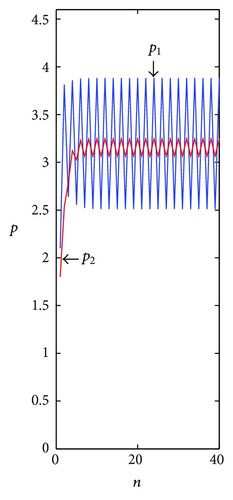
Figure 3 shows the price evolution with time when the dynamical system (15) is in the stable (α1 = 0.5), period-doubling bifurcations (α1 = 0.8), and chaotic state α1 = 1.0. As can be seen from Figure 3(a), along with the continuation of competitive cycle, the price of two firms will be stable in equilibrium state gradually after a series of fluctuation. And the price evolves into 2-period orbit gradually in Figure 3(b). But in Figure 3(c), the price is in chaos and takes on unordered change.

Details are in the caption following the image
Figure 3 (a)
Open in figure viewerPowerPoint
Time sequence diagrams under different states.
Details are in the caption following the image
Figure 3 (b)
Open in figure viewerPowerPoint
Time sequence diagrams under different states.
Details are in the caption following the image
Figure 3 (c)
Open in figure viewerPowerPoint
Time sequence diagrams under different states.

We draw the two-dimension flip bifurcation diagram in the parameters α1 and a (Figure 4(a)) and α1 and c1 (Figure 4(b)). In Figure 4, the Nash equilibrium is stable when the parameters α1, a, and c1are in the cyan-shaped area (stability region) and loses its stability with increasing value of α1. And the two-flip bifurcation cures are inverse function cures. This demonstrates what was mentioned above that stability region of the Nash equilibrium point is a decreasing function with respect to the market capacity a and the marginal cost c1.

Details are in the caption following the image
Figure 4 (a)
Open in figure viewerPowerPoint
Flip bifurcation curves in the parameters α1 and a (a) and α1 and c1 (b).
Details are in the caption following the image
Figure 4 (b)
Open in figure viewerPowerPoint
Flip bifurcation curves in the parameters α1 and a (a) and α1 and c1 (b).

Figure 5 shows the price evolution process with respect to α2 (the speed of adjustment of the boundedly rational follower) of dynamical system (15) when α1 = 0.5. In Figure 4, the price is unalterable all the while and the dynamical system (15) is always locally stable. And this also demonstrates that the speed of adjustment of the boundedly rational follower has no effect on the game model.

Details are in the caption following the image
Figure 5
Open in figure viewerPowerPoint
Evolution diagram with respect to α2 when α1 = 0.5.

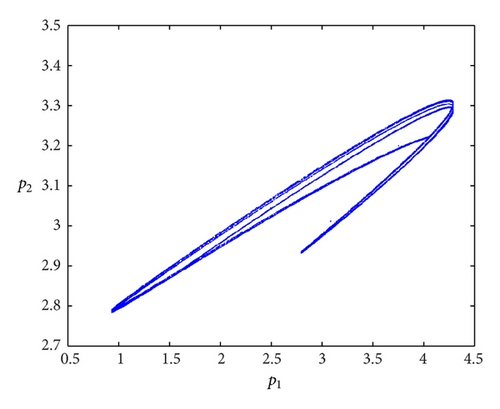
Strange attractor is one of the main features of chaotic motion. It exhibits fractal structure. Figure 6 shows the strange attractor in the phase plane (q1, q2) for the parameter values  a = 2, b = 0.5, c1 = 0.2, c2 = 0.4, α1 = 1.07, and α2 = 0.5.

Details are in the caption following the image
Figure 6
Open in figure viewerPowerPoint
Strange attractor when α1 = 1.01 and α2 = 0.5.

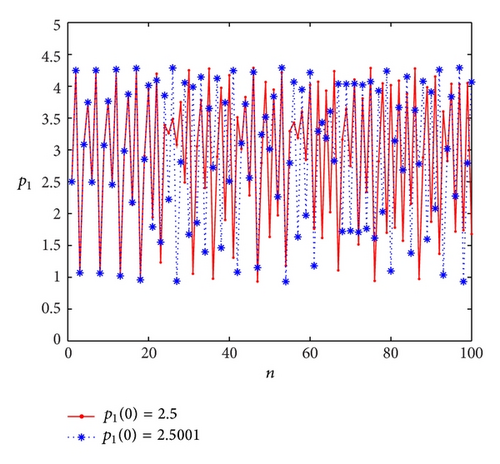
Sensitive dependence on initial conditions is another main characteristic of chaotic system. In order to demonstrate sensitive dependence on initial conditions of system (10), we simulate two orbits in Figure 7 for the parameter values  a = 2, b = 0.5, c1 = 0.2, c2 = 0.4, α1 = 1.01, and α2 = 0.5. The red and blue curves start from the initial points (p1(0), p2(0)) = (2.5, 2.3) and (p1(0), p2(0)) = (2.5001,2.3), respectively. It shows that, at the beginning, they are indistinguishable, but after a number of iterations, the difference between them builds up rapidly.

Details are in the caption following the image
Figure 7
Open in figure viewerPowerPoint
Shows sensitive dependence on initial conditions; the two orbits of p1-coordinates for (a, b, c1, c2, d, α1, α2) = (2,0.5,0.2,0.4,0.3,1.01,0.5) with (p1(0), p2(0)  ) = (2.5, 2.3) for the red curve and (p1(0), p2(0)  ) = (2.5001, 2.3) for the blue curve.

5. Conclusion

In this paper we have proposed a price Stackelberg duopoly game model with boundedly rational players. The complex dynamical behaviors have been studied. In Nash equilibrium, the price of the leader is less than the follower’s and also less than equilibrium price of Bertrand game under the same assumption. The theoretical and numerical analysis shows the result that the stability of the dynamical system (15) is only relevant to the speed of price adjustment of the boundedly rational leader and not relevant to the follower’s. Definitely, the speed of price adjustment of the boundedly rational leader has a destabilizing effect and the follower’s has no effect on the dynamical system. This is different from the classical Cournot and Bertrand duopoly game with bounded rationality. Perhaps the reason of this is the Stackelberg-type game structure. The other type of price Stackelberg game, such as with heterogeneous player or different competition strategies, will be studied in future work.

Conflict of Interests

The authors declare that there is no conflict of interests regarding the publication of this paper.

Acknowledgments

The authors would like to thank the anonymous referees very much for their valuable comments and suggestions. This work was supported by Major Program of National Natural Science Foundation of China (71390521 and 71390523) and by National Natural Science Foundation of China (71101067, 71271103, 71301062, and 71301070).

      The full text of this article hosted at iucr.org is unavailable due to technical difficulties.