Abstract and Applied Analysis
Volume 2014, Issue 1 410282
Research Article
Open Access

Global Multivariable Control of Permanent Magnet Synchronous Motor for Mechanical Elastic Energy Storage System under Multiclass Nonharmonic External Disturbances

Yang Yu, 

Corresponding Author

Yang Yu

State Key Laboratory of Alternate Electrical Power System with Renewable Energy Sources, North China Electric Power University, Baoding 071003, China ncepu.edu.cn

Search for more papers by this author
Zengqiang Mi, 

Zengqiang Mi

State Key Laboratory of Alternate Electrical Power System with Renewable Energy Sources, North China Electric Power University, Baoding 071003, China ncepu.edu.cn

Search for more papers by this author
Yikun Xu, 

Yikun Xu

State Key Laboratory of Alternate Electrical Power System with Renewable Energy Sources, North China Electric Power University, Baoding 071003, China ncepu.edu.cn

Search for more papers by this author
Tong Zhao, 

Tong Zhao

State Key Laboratory of Alternate Electrical Power System with Renewable Energy Sources, North China Electric Power University, Baoding 071003, China ncepu.edu.cn

Search for more papers by this author
First published: 26 May 2014
https://doi.org/10.1155/2014/410282
Citations: 3
Academic Editor: Shuping He

Abstract

For the technology of mechanical elastic energy storage utilizing spiral torsion springs as the energy storage media presented previously, a global multivariable control algorithm based on nonlinear internal model principle under multiclass external disturbances is proposed. The nonlinear external disturbances with nonharmonic periodic characteristics are generated by multiclass nonlinear external systems. New equations of nonlinear internal model are designed to estimate the multiclass external disturbances. On the basis of constructing the control law of nominal system, a state feedback controller is designed to guarantee the closed-loop system globally uniformly bounded, and a Lyapunov function is constructed to theoretically prove the global uniform boundedness of the multivariable closed-loop system signals. The simulation results verify the correctness and effectiveness of the presented algorithm.

1. Introduction

Energy storage technologies have a great practical significance for the solution of new energy interconnecting to the grid, peak regulation, frequency modulation, and stability control [1, 2]. Based on lucubration of mechanical elastic energy storage (MEES), a new way of MEES method applying spiral torsion springs (STS) as the energy storage material is proposed [3]. Due to the advantages such as large power density, high efficiency, great electromagnetic torque, small volume, and fast response speed, permanent magnet synchronous motor (PMSM) is selected as the actuator for MEES system, just as in many other servo systems [4]. One of the key technologies to be solved for MEES is the nonlinear control owing to its electromechanical coupling properties and nonlinear characteristics of PMSM [5]. When PMSM based MEES system runs in energy storage, the increasing load torque with the tightening of STS is unfavorable for the operation of servo system. In addition, due to the nonlinearities, strong coupling, and time variation of PMSM, especially the existence of the nonlinear external disturbances, the conventional PID controller is difficult to satisfy the requirement of high precision control [6]. Hence, the other control methods should be introduced, just as nonlinear control [7–10], adaptive control [11], state feedback control [12], and so forth.

One of the core questions in control field is to guarantee asymptotical stability of unforced close-loop system, implement the asymptotical tracking of system output for given trajectories, and reject exogenous disturbances [13–16]. The control problems for servo system are also called the output regulation problems; the problems of disturbance rejection under the framework of output regulation have earned extensive attention in recent years [17, 18]. The preexisting papers mostly assumed that the exosystem generating disturbances is linear, neutral, and stable; that is to say, disturbance rejection under sinusoidal perturbation is frequently studied. For instance, literatures [16, 17, 19] deal with the problems of sinusoidal perturbation rejection in known and unknown frequency, respectively. Nevertheless, the nonharmonic disturbances generated by nonlinear exosystems, which will make practical servo systems, generators, and power flexible mechanisms produce noise and precision reduction [20], are harmful to these practical running systems. However, how to tackle with disturbances generated by nonlinear exosystems is rarely involved [21]. Therefore, rejection of these harmful oscillations is essential to guarantee that the systems operate stably under nonlinear external disturbances.

Another central issue in control field is to extend the established control theory to more complex and generalized circumstances. In [22], disturbance rejection under a class of exosystems for a single-input nonlinear system is studied, in which the dependent external system is a single model, and the researched system is a single-input system. In [23], a global harmonic rejection algorithm for multivariable system is proposed; however, the rejection of the disturbances in the paper aims at the standard sinusoidal components. For the nonlinearity and complexity of PMSM based MEES system, the focus of the paper is to extend the previous works in [22, 23] to a generalized multivariable input field of nonlinear systems under multiclass nonlinear exosystems with the application of the constructed model for PMSM based MEES system in [5] and design a controller to suppress multiclass external nonharmonic disturbances in PSMS based MEES system.

The mainly theoretical contribution of the paper is to propose a global multivariable disturbance control method to reject multiclass nonlinear external nonharmonic disturbances generated by multiclass nonlinear exosystems for general multivariable nonlinear system, and the presented control algorithm is employed to regulate an actual nonlinear system. The validity and effectiveness of the proposed method are testified by the simulation results.

The organization of the paper is as follows. It starts with an introduction of the research status of disturbance rejection and points out the significance of rejection of nonharmonic external disturbances in Section 1. The mathematical model of PMSM based MEES system is constructed and the formulation of control problem in the paper is given in Section 2. In Section 3, the nonlinear internal models simulating the multiclass external nonharmonic disturbances are presented based on internal model principle. Nonlinear multivariable state feedback controller ensuring the closed-loop system globally bounded is demonstrated in Section 4. The verifications of the proposed algorithm by means of numerical simulations are shown in Section 5. Ultimately, Section 6 sums up the conclusions of the research and puts forward the work in the future.

2. Problem Formulation

2.1. Mathematical Model of PMSM Based MEES System

For the convenience of understanding and reutilization, the model of the whole system for PMSM based MEES system proposed in [3, 5] is shown in Figure 1, where gear case is simplified as a model of spring mass damper with multidegree of freedom, Bm and BL denote the damping coefficients of the motor and elastic shaft, respectively, Tm and TL represent the output torque of the motor and main shaft, respectively, and ωm and ωL symbolize the angular velocity of the motor and main shaft of energy storage box, respectively. STS is installed in energy storage box.

Details are in the caption following the image
Figure 1
Open in figure viewerPowerPoint
The model of PMSM based MEES system.
In the process of energy storage, PMSM runs in the state of electric motor. For PMSM, assume that the inductance of d-axis Ld is equal to the inductance of q-axis Lq. Accordingly, the mathematical model for PMSM in dq rotating coordinates can be expressed as follows [24]:
(1)
where id and iq denote the current components of stator in dq axis, respectively, ud and uq display the voltage components of stator in dq axis, respectively, and Rs, ωm, φf, p, and Jm represent the resistance of stator, angular velocity, flux linkage of rotor, numbers of pole pairs, and moment of inertia of rotor, respectively.
The ratio of gear case is assumed to be r; without regard to the power loss of gear case, the relationship between torque and angular velocity on both sides of gear case can be expressed as
(2)
Suppose the outer end of STS to be fixed in spring box as V type, and in terms of the national standard design and calculation of spiral torsion spring (JB/T7366-1994) in China, the torque of STS with rectangle cross section can be written as
(3)
where n denotes the working turns of spring, E,  l,  b, and h represent the modulus of elasticity, length, width, and thickness of STS, respectively, and k indicates mass coefficient of spring.
Due to the large mass and high inertia of MEES system, the working rotation velocities for the main shaft of energy storage box and the rotor of PMSM are both assumed to be invariable. Hence, the relationship between the angular velocity ωL and the working turns n for the main shaft of energy storage box can be written as follows:
(4)
where t represents the time.
Equation (4) is substituted into (3); the relationship between the torque TL of STS and angular velocity ωL of the main shaft can be given by the following formula:
(5)

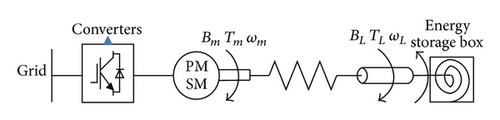
For a given STS, (5) shows that the torque TL of STS is proportional to the time t if angular velocity ωL is a constant.

The mathematical model for the whole system of PMSM based MEES can be obtained by combining differential equation (1) with algebraic equations (2) and (5).

2.2. Control Problem Formulation

Consider the multivariable nonlinear system with a standard affine form under multiclass disturbances:
(6)
where x ∈ Rn are the state vectors, ui ∈ R are the control inputs, f(x) and gi(x) are the known smooth vector fields, vi(w) are the nonlinear disturbance inputs, and w ∈ Rq indicate the external signals generated by the nonlinear exosystem shown as follows:
(7)
If the nonlinear disturbance inputs are ignored, for system (6), its nominal system can be written as
(8)

The essence of solving stability problems for a multivariable input system is to convert these problems into the stability problems of multiple single-input systems [25].

Assumption 1. For system (8), there exists a control law of state feedback αi(x) making the nominal close-loop system asymptotically stabilize at the origin. Therefore, there exists a Lyapunov function V(x) satisfying

(9)
where , , and d0 are all of K∞ class functions.

Assumption 2. The trajectory of the vector field for the nonlinear exosystem (7) is bounded.

Remark 3. The functions, which meet Assumption 2, include harmonic functions and limit cycles of nonlinear dynamic systems. For instance, the famous Van der Pol circuit can be written as

(10)
where ς denotes a parameter to adjust the period of current or voltage. The eigenvalues of Jacobian matrix for (10) at the origin are . If 0 < ς ≤ 2, the eigenvalues have positive real parts; if ς > 2, the eigenvalues are positive real numbers. Consequently, as long as ς > 0, the equilibrium points at the origin of (10) are unstable and there exists a bounded limit cycle [20].

Assumption 4. There exists a smooth function ri(x) : Rn → Rq making

(11)
where Ki ∈ Rq is a nonzero constant vector.

The problem to be solved in the paper can be described as in the following definition.

Definition 5. For any given compact subset Dw ∈ Rq, a state feedback controller ui can be found to make the solution of the close-loop system (6) exist and be bounded, and lim⁡t→∞x(t) = 0 under arbitrary initial conditions for all w(0) ∈ Dw and t ≥ 0.

3. Multiclass Nonlinear Internal Models Design

In the paper, internal model principle (IMC) is utilized to reject the multiclass disturbances. Disturbances rejection by IMC belongs to indirect suppression algorithm. Hence, appropriate internal model equations should be firstly established to estimate the inputting nonlinear disturbances. Because the exosystem discussed in the paper is nonlinear, the internal model equations established should also be nonlinear. Therefore, Assumption 6 is introduced as follows.

Assumption 6. For the nonlinear exosystem (7), when 1 ≤ i ≤ m, there exists an immersion system being depicted as follows:

(12)
where ηi ∈ Rr,  Fi,  Gi,  Hi,  Ji are matrices with certain dimensions, the matrix pair (Fi, Hi) is observable, and there exists a positive definite matrix making the following formula hold:
(13)
and the nonlinear function γi(Jiηi) can be expressed as
(14)
and satisfies .

Consequently, the multiclass nonlinear internal model equations can be designed as follows:
(15)
where Ki ∈ Rq satisfies Assumption 4 and makes Fi0 = Fi − KiHi a Hurwitz matrix; hence there exist positive definite matrices and satisfying the following equation:
(16)
Define an auxiliary error ei as follows:
(17)
and derivative of (17) along with (6), (12), and (15) is given by
(18)

4. State Feedback Controller Design

In terms of the nonlinear internal models shown in (15) and Assumption 1, the state feedback controller can be designed as follows:
(19)
where αi(x) is a controller being able to stabilize the nominal system (8).
Construct a Lyapunov function as follows:
(20)
Derivative of Lyapunov function W along with system (6) and auxiliary error (18), we can obtain
(21)
where λmin⁡(·) denotes the minimum eigenvalue of a certain matrix.
In terms of Assumption 6, we can obtain ; hence
(22)
Applying permanent establishment inequality 2ab ≤ ca2 + c−1b2 (choosing c = 2) to the second term of (21), we obtain
(23)
Substitute (22) and (23) into (21) and combine (23) with the application of Assumption 1; we obtain
(24)
Choose appropriate and Hi to satisfy
(25)
namely,
(26)

By above knowable, all the variables are bounded. Combine with the application of the invariant set theorem, it can be obtained that lim⁡t→∞x(t) = 0 and lim⁡t→∞ei = 0. Therefore, we give a theorem as follows.

Theorem 7. There exist positive definite matrices and satisfying (13) and (16), nonzero vector Ki ∈ Rq makes Fi0 = Fi − KiHi be Hurwitz, and (25) holds as well. Hence, for the multivariable nonlinear system (6) and multiclass exosystem (7) satisfying Assumption 1 to Assumption 6, the multiclass nonlinear internal models (15) and control inputs (19) are able to make the close-loop system globally uniformly hounded, and lim⁡t→∞x(t) = 0.

Remark 8. Theorem 7 redescribes Definition 5 in essence; furthermore, it provides a feasible way to find a state feedback controller ui to stabilize the close-loop system (6) to reference trajectories. In addition, the selection of positive definite matrices   and and nonzero vector Ki is to design multiclass nonlinear internal models (see (15)) to simulate the external nonharmonic disturbances produced by nonlinear exosystem shown in (7). The control inputs (19) are the state feedback controller described in Definition 5.

5. Numerical Simulation and Analysis

5.1. Description of Simulation Parameters

The verification of the proposed algorithm in the paper is performed by means of numerical simulation in a 0.018 kWh/1.1 kW PMSM based MEES system. The specific parameters of the MEES system are shown as follows: the rating torque of PMSM Tm = 5.0 N.m, number of pole-pairs p = 4, flux linkage of rotor φf = 0.18 Wb, resistance of stator Rs =  1.95 Ω, inductances of d-axis and q-axis Ld = Lq = 0.0115 H, moment of inertia of rotor Jm = 0.008 kg·m2, ratio of gear case = 40 : 1, the angular velocity of main shaft ωL = 15 r/min, and damping coefficients of the motor Bm = 0.01 N/rad/s.

5.2. Analysis and Discussion of Simulation Results

Considering the multiclass nonlinear disturbances, the mathematical model for the whole system of PMSM based MEES system is converted into the form of (6), and the ultimate result is shown in (27). Equation (27) indicates that the nonlinear model of MEES system is a two-variable input system, which is unable to be dealt with by a single-input algorithm. In addition, (27) includes multiclass nonlinear disturbances vi(w), and the rejection algorithm handling a single disturbance cannot address the problem of multiclass disturbances rejection as well:
(27)
where ,
(28)
and the control input .
If the nonlinear disturbances vi(w) are ignored in (27), the remaining system in (29) is the nominal system for MEES system:
(29)

For the sake of convenience, the inputs of nonlinear external disturbances v1 and v2 are both generated by Van der Pol circuit described in (10) with ς = 2, which produces bounded limit cycles. Consequently, Assumption 2 holds.

Suppose that v1 and v2 are immersed in the current components of d-axis and q-axis, respectively, and v1 = w1, v2 = w1 − w2. Hence, the difference of the external disturbances represents the fact that the original system is immersed in multiclass nonlinear disturbance signals. For v1, the matrix parameters appearing in (12) are chosen as
(30)
for v2 = w1 −  w2, the matrix parameters appearing in (12) are selected as
(31)
and hence Assumption 6 is satisfied.
Assume that c1, c2, and c3 all are certain positive constants; the control law for the nominal system (29) is designed as
(32)
where ωref denotes the angular velocity reference of rotor for PMSM. It can be verified that α(x) can stabilize the nominal system (29) without disturbances, owing to the fact that the stabilization process of (29) is not the emphasis of the paper; hence the detailed deductions are omitted.
Let
(33)
after calculations and arrangements, we obtain
(34)
(35)
Supposing that
(36)
according to (33), (34), and (35), and choosing c1 = 8000, c2 = 40, and c3 = 8000, we obtain
(37)
(38)
(39)
Hence, Assumption 1 holds.
Choose
(40)
Consequently,
(41)
Therefore, Assumption 4 is satisfied. In addition, with the application of (41), Fi0 and in (16) can be shown as follows by means of some calculations:
(42)
The above analysis has verified that MEES system (27) and system (10) of the external disturbances satisfy all the conditions required by Theorem 7. Consequently, based on the multivariable disturbances rejection algorithm proposed in the paper, the multiclass nonlinear internal models and state feedback controller are designed as follows:
(43)

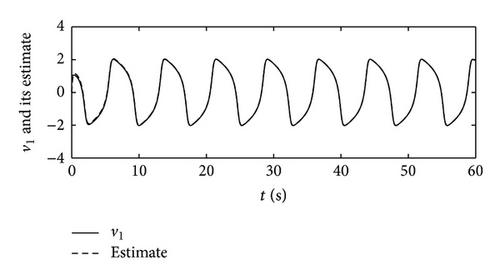
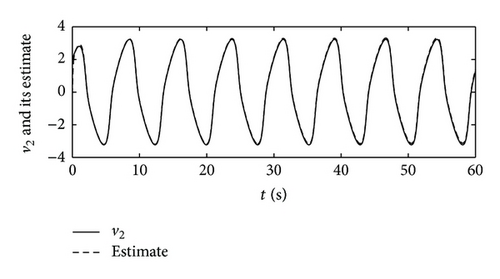
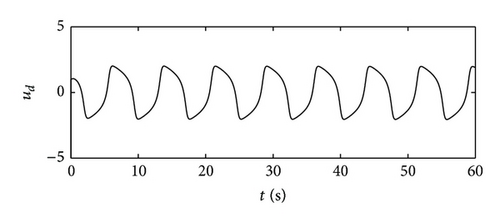
The numerical simulations are conducted in Matlab environment. The whole simulation time is set as 60 s with the sampling interval 0.001 s; let the initial condition of the simulation be , , and . The reference values of the d-axis current id and angular velocity of the motor ωm are selected as 0 and 600 r/min, respectively. The q-axis current iq tracks the change of the torque of STS in energy storage. The simulation results are shown in Figures 2, 3, and 4. Figure 2 demonstrates the multiclass nonlinear disturbance inputs and their estimations, from which it can be seen that the multiclass nonlinear disturbances acting on the different state variables in a multivariable input system are successfully estimated relying on the internal models designed. Figure 3 displays the control inputs of the system in dq axis under the existence of multiclass nonlinear external disturbances. Figure 4 describes the system states, which indicates that the system achieves the asymptotical tracking for the reference signals rapidly and the multiclass nonlinear disturbances are completely suppressed. Hence, the multivariable controller designed in the paper has a good control performance.

Details are in the caption following the image
Figure 2 (a)
Open in figure viewerPowerPoint
Nonlinear disturbance inputs v and their estimates.
Details are in the caption following the image
Figure 2 (b)
Open in figure viewerPowerPoint
Nonlinear disturbance inputs v and their estimates.
Details are in the caption following the image
Figure 3 (a)
Open in figure viewerPowerPoint
System control inputs u.
Details are in the caption following the image
Figure 3 (b)
Open in figure viewerPowerPoint
System control inputs u.
Details are in the caption following the image
Figure 4 (a)
Open in figure viewerPowerPoint
System states x.
Details are in the caption following the image
Figure 4 (b)
Open in figure viewerPowerPoint
System states x.
Details are in the caption following the image
Figure 4 (c)
Open in figure viewerPowerPoint
System states x.

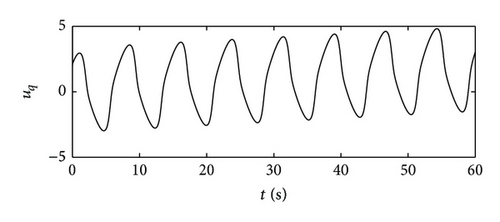
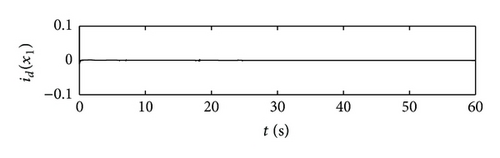
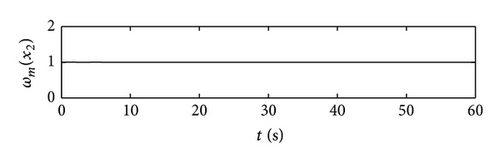
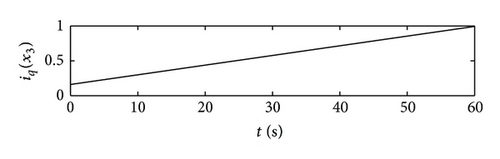
6. Conclusion

In light of the strong coupling and nonlinear characteristics of PMSM based MEES system, a global multiclass nonharmonic disturbances rejection method for general multivariable nonlinear system under multiclasses nonlinear exosystems is proposed in the paper. For multiclass nonlinear external disturbances with different periodic bounded nonharmonic characteristics, different nonlinear internal model equations are designed. Based on design of control law for nominal system, a state feedback controller for original system is presented and a Lyapunov function is established to theoretically testify the global boundedness of all signals in multivariable close-loop system. The simulation results show that the multiclass different nonlinear disturbance inputs are all completely rejected and the close-loop system can track the reference signals promptly. Consequently, high accuracy servo control for PMSM based MEES system is realized.

In addition to PMSM based MEES system, many other practical engineering systems, including turbine motor, generator, power flexible manipulator, and communication circuit, are frequently affected by the nonharmonic disturbances generated by the external nonlinear exosystems. As the most famous and typical nonlinear circuit, Van der Pol circuit researched in the paper will excite nonharmonic disturbances and make the system mentioned above produce nonharmonic forced oscillation. The algorithm presented in the paper can eliminate the harmful oscillation and improve the stability for these practical systems.

The critical points of the output regulation problem under nonharmonic disturbances are to model the nonlinear exosystems and propose reasonable algorithm to stabilize the closed-loop system. In the future, the proposed algorithm in the paper can be able to be extended to uncertainly multivariable systems and unknown external signals; correspondingly, the innovative control technologies should be researched to cope with the more complex and generalized circumstances.

Conflict of Interests

The authors declare that there is no conflict of interests regarding the publication of this paper.

Acknowledgments

This work was supported by the National Natural Science Foundation of China (Grant no. 51077053), the Specialized Research Fund for the Doctoral Program of Higher Education of China (Grant no. 20120036130001), the Fundamental Research Funds for the Central Universities of China (Grant no. 2014MS93), and the Independent Research Funds of State Key Laboratory of Alternate Electrical Power System with Renewable Energy Sources of China (Grant no. 201209).

      The full text of this article hosted at iucr.org is unavailable due to technical difficulties.