International Journal of Partial Differential Equations
Volume 2014, Issue 1 407387
Research Article
Open Access

Numerical Solutions of Two-Way Propagation of Nonlinear Dispersive Waves Using Radial Basis Functions

Pablo U. Suárez, 

Corresponding Author

Pablo U. Suárez

Department of Mathematical Sciences, Delaware State University, Dover, DE 19901, USA desu.edu

Search for more papers by this author
J. Héctor Morales, 

J. Héctor Morales

Departamento de Matemáticas, UAM Iztapalapa, Apartado Postal 55-534, 09340 Iztapalapa, DF, Mexico uam.mx

Search for more papers by this author
First published: 03 August 2014
https://doi.org/10.1155/2014/407387
Citations: 2
Academic Editor: Nikolai A. Kudryashov

Abstract

We obtain the numerical solution of a Boussinesq system for two-way propagation of nonlinear dispersive waves by using the meshless method, based on collocation with radial basis functions. The system of nonlinear partial differential equation is discretized in space by approximating the solution using radial basis functions. The discretization leads to a system of coupled nonlinear ordinary differential equations. The equations are then solved by using the fourth-order Runge-Kutta method. A stability analysis is provided and then the accuracy of method is tested by comparing it with the exact solitary solutions of the Boussinesq system. In addition, the conserved quantities are calculated numerically and compared to an exact solution. The numerical results show excellent agreement with the analytical solution and the calculated conserved quantities.

1. Introduction

Consider the initial and boundary value problem
()
()
()
()
()
where a, b, c, and d are real constants and subscripts x and t denote space and time derivatives, respectively. In fluid mechanics, the functions v and u represent flow velocities. Solutions of this type of systems have attracted much research in the past two decades [1–9]. In these studies the most popular system of Boussinesq type is the one proposed by Bona and Chen in [1], to describe approximately the two-dimensional propagation of surface waves in a uniform horizontal channel of a fixed length filled with an irrotational, incompressible, and inviscid flow. The system is derived formally from Euler’s equations in 2D and using small amplitude and long wave length assumptions. Further, solitary wave solutions of this system have been reported in numerous works; see for instance [1, 2, 6, 10].

This work studies the numerical solution of this system by means of radial basis functions (RBFs). The use of these types of basis functions has become very popular in recent times; see for instance the work of Buhmann [11], Franke and Schaback [12], Driscoll and Heryudono [13], and the references therein. The main inspiration for this work is the very successful application of RBFs to solve the Kawahara equation [14] and the modified regularized long wave equation (MRLW) [15].

We will examine the two cases for the Boussinesq type system. The first one we examine is the Bona and Chen system, which is important in the theory of dispersive waves,
()
This corresponds to the case a = c = 0 with b = d = 1/6. The second case we examine is the full system with a = −7/30,  b = 7/15, c = −2/5, and d = 1/2:
()
The paper is organized in three sections. In Section 2, we use RBFs to reduce the PDE system to a system of differential equations. In Section 3, we use a linear multistep method to solve these ODEs and then proceed to compute several conserved quantities of the PDE system. We provide comparative tables in order to show the accuracy of the RBFs approach. Finally, in Section 4, we discuss some conclusions.

2. The Method of Lines for Radial Basis Functions

The RBFs approach is one of the most effective meshless methods to solve numerically PDEs. The key feature of the RBFs is that its implementation does not require a mesh at all. The method employs approximants whose values depend only on the distance between some center point and a domain point, in an appropriate norm. Due to the use of the distance functions, we can control the convergence up to an order proportional to the spacing of two points where we evaluate such functions [16].

The functions v(x, t) and u(x, t) in (1) and (2) are approximated using n-terms RBFs:
()
()
where λj(t) and μj(t) are time-dependent functions to be determined and ϕj(x): = ϕ(∥x − xj∥) is a radial basis functions to be specified. We adopt the Euclidean L2-norm ∥·∥2 in this work to denote distance between the point xj, referred as center of the RBFs, and x, the free spatial variable, at which we can evaluate the approximant. Some examples of the RBFs are [11, 15]
()
where the parameter φ is proportional to the amplitude of the RBF at x = xj, and it is under our control [11]. These RBFs have shown to be successful in solving nonlinear PDEs with mixed partial derivatives [15, 17].
In terms of the RBFs, we can find the derivatives of the approximate solution of n terms as follows:
()
as well as for un.
If we substitute (8)–(11) into (1)-(2), we obtain a system of two coupled nonlinear ordinary differential equations for λj(t) and μj(t):
()
()
where ϕj(x) = ϕ(∥x − xj∥).
We solve the system over the real line −∞ ≤ x ≤ ∞ and on a finite time 0 ≤ t ≤ τ. We first truncate the spatial interval to a finite computational domain −L ≤ x ≤ L and specify m + 1 collocation points x0, x1, …, xm. We then employ these equally-spaced collocation points xi = −L + iΔx, i = 0, …, m; Δx = 2L/m and introduce the matrix notation
()
()
()
()
the vector superscript T denotes the transpose. We then obtain a 2(m − 1) × 2(n − 1) ODE system that can be compactly written in the form
()
where M is called a mass matrix, Γ is called the drift matrix, and F is in general a nonlinear term dependent on t and y(t). The vector y(t) is defined by y(t) = [λ(t),μ(t)]T. Explicitly, we have
()
The elements of F must be explained. The spatial derivative (15), Dk, with k = x, xx or xxx, is acting element by element on a matrix and does not modify its size. The products Φμ and Φλ are vectors of size (m − 1) × 1 each; however, its product is element by element according to the right-hand side of (12), after the expression is evaluated in a particular collocation point xi. Therefore, −Dx(ΦμΦλ) and −Φμ(DxΦ)μ are vectors of size (m − 1) × 1.
Additionally, the discretization of the boundary conditions, equations (3) and (4), provide four algebraic equations:
()
and the initial conditions (5) provide us with two algebraic equations:
()
To solve the system (18), we use the fourth-order Runge-Kutta Method (RK4) and let m = n. We can rewrite (18) as
()
where f(y, t) = M−1(−Γy(t) + F(t, y(t))).
The classical RK4 algorithm for a system of ODEs is given by
()
where
()

The RK4 scheme does not have stability issues as long as the time step Δt is chosen sufficiently small. The selection of the time step is done by the following [18].

Rule of Thumbs. The method of lines is stable if the eigenvalues of the linearized spatial discretization operator, scaled by Δt, lie in the stability region of the time-discretization operator.

For the stability analysis nonlinearity in (22), F(t, y(t)) is set to zero and we compute the eigenvalues of M−1Γ. So the method is stable as long as the eigenvalues are in the stability region (−2.76 < Δtλj < 0). In order to have a stable scheme, we adjust the parameter φ so that the matrices remain in the region of stability. This was carried out in the numerical experiments.

3. Numerical Approximations of Boussinesq System

In this section, we use the proposed algorithm to calculate the numerical solution of the Boussinesq type system and its conserved quantities. These quantities were performed by means of the trapezoidal quadrature. The accuracy of the method is tested by computing the L2 and L∞ (error norms) defined as
()
where and stand for numerical evaluation of the exact solution and numerical approximation of the solution, respectively. The test cases in this section are solved over the domain −50 ≤ x ≤ 50 in the time period 0 < t ≤ 20. The domain and time period are discretized with values Δx = 0.25 and Δt = 0.2, respectively. The initial conditions are taken from the exact solution at the value t = 0.

The integrals involving the conserved quantities were calculated by using the Trapezoidal rule.

3.1. Numerical Benchmark

The first test problem was studied extensively by Chen in [2]. This case is important in the theory dispersive waves. A solitary wave solutions is known and is given by Chen in [2]:
()
This case has four conserved quantities derived in [4]:
()
In Tables 1 and 2 we have the error norms at time t = 15 for v(x, t) and u(x, t), respectively. We also measure the amplitude for v(x, t) and the peak-to-peak (P-P) amplitude for u(x, t). Table 3 shows the analytical and numerical value of the conserved quantities. The tables show excellent agreement with the exact solution. We can see that using multiquadratic and Gaussian quadratic RBFs is more accurate in approximating the solution which is in agreement with the work of Dereli [15] for MRLW equation. In addition to these tables, we see in Figure 1 how the approximate solution is “lying” closely to the analytical one. Figure 2 shows that as we increase the number of collocation points the error reduces.
Table 1. Error norms of v(x, 15).
Method φ L2 error of v L∞ error of v Amplitude v x
Analytic — — — 7.462309 37.43
MQ 1.23  3.074E − 05   2.721E − 05  7.462316 37.43
G 2.66  5.395E − 05   4.783E − 05  7.462310 37.43
IQ 1.00  2.244E − 03   2.129E − 03  7.462390 37.43
IMQ 2.05  2.450E − 03   1.224E − 03  7.462565 37.43
Table 2. Error norms of u(x, 15).
Method φ L2 error of u L∞ error of u Amplitude (P-P) u xmin⁡ xmax⁡
Analytic — — — 4.91342 36.23 37.43
MQ 1.23 3.381E − 05   2.606E − 05  4.91343 36.23 37.43
G 2.66 5.747E − 05   5.358E − 05  4.91339 36.23 37.43
IQ 1.00 2.313E − 03   2.204E − 03  4.91575 36.23 37.43
IMQ 2.05 2.804E − 03   1.950E − 03  4.91481 36.23 37.43
Table 3. Conserved quantities.
Method I1 I2 I3 I4
Analytic 15.81139 0.0000 158.113 −22.5876975726
MQ 15.81134 −2.07E − 05  158.113 −22.58776106781
G 15.81139 −1.31E − 09  158.113 −22.58776062211
IQ 15.81144 −2.87E − 04  158.168 −22.58432200892
IMQ 15.81156 6.92E − 04  158.152 −22.58512792633
Details are in the caption following the image
Figure 1
Open in figure viewerPowerPoint
Comparison of v(x, t) and u(x, t) with exact solution using MQ RBFs.
Details are in the caption following the image
Figure 2 (a) Evolution of v(x, t)
Open in figure viewerPowerPoint
Soliton interaction of Boussinesq type system.
Details are in the caption following the image
Figure 2 (b) Evolution of u(x, t)
Open in figure viewerPowerPoint
Soliton interaction of Boussinesq type system.

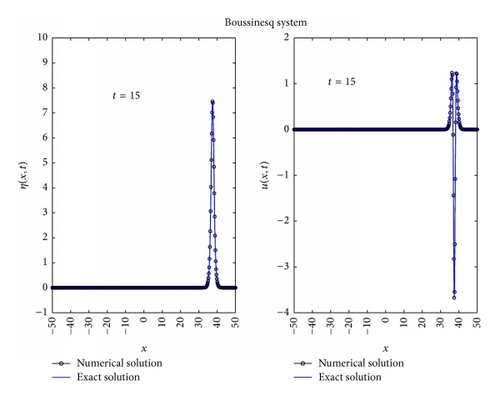
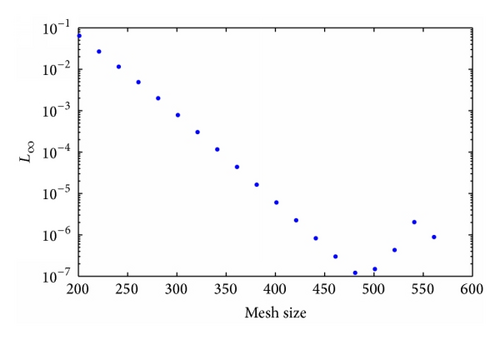
3.2. Problem

In this example we test our algorithm with a solution against the “full system” equations (7). A solitary wave solution to the “full system” is presented in [7]. The solution is as follows:
()
The boundary conditions are the same as the BBM and the conserved quantities are
()
Tables 4, 5, 6, and 7 show the L2 and L∞ error for various times of v(x, t) and u(x, t) along with the conserved quantities of the equations. Once again the numerical solution and the analytical solution are in good agreement.
Table 4. Error norms and conserved quantities for v(x, t) and u(x, t).
Time L2 error of v L∞ error of v L2 error of u L∞ error of u I1 I2
MQ            
 0.5  3.467E − 08   4.122E − 08   4.437E − 08   5.202E − 08  1.7748239 1.6733200
 1.0  1.544E − 07   1.766E − 07   1.892E − 07   2.231E − 07  1.7748238 1.6733198
 2.0  3.061E − 07   3.130E − 07   3.372E − 07   3.550E − 07  1.7748235 1.6733196
 3.0  3.960E − 07   3.480E − 07   4.206E − 07   3.796E − 07  1.7748233 1.6733193
 4.0  4.585E − 07   3.600E − 07   4.762E − 07   3.825E − 07  1.7748231 1.6733195
 5.0  4.501E − 07   3.490E − 07   4.604E − 07   3.689E − 07  1.7748232 1.6733192
 10.0  4.758E − 07   2.765E − 07   4.881E − 07   2.864E − 07  1.7748237 1.6733193
 15.0  5.607E − 07   2.351E − 07   5.715E − 07   2.400E − 07  1.7748246 1.6733198
 20.0  7.205E − 07   2.102E − 07   7.300E − 07   2.138E − 07  1.7748260 1.6733205
 25.0  1.116E − 06   3.704E − 07   1.143E − 07   3880E − 07  1.7748285 1.6733212
 30.0  4.239E − 06   6.321E − 06   4.954E − 06   5.960E − 06  1.7748236 1.6733103
Table 5. Error norms and conserved quantities for v(x, t) and u(x, t).
Time L2 error of v L∞ error of v L2 error of u L∞ error of u I1 I2
G            
 0.5  2.268E − 10   1.442E − 10   2.188E − 10   1.425E − 10  1.7748239 1.6733200
 1.0  4.548E − 10   2.948E − 10   4.351E − 10   2.877E − 10  1.7748238 1.6733198
 2.0  9.045E − 10   5.976E − 10   8.672E − 10   5.848E − 10  1.7748235 1.6733196
 3.0  1.343E − 09   9.038E − 10   1.295E − 09   8.901E − 10  1.7748233 1.6733193
 4.0  1.775E − 09   1.195E − 09   1.710E − 09   1.172E − 09  1.7748231 1.6733195
 5.0  2.194E − 09   1.476E − 09   2.113E − 09   1.445E − 09  1.7748232 1.6733192
 10.0  4.065E − 09   2.570E − 09   3.909E − 09   2.490E − 09  1.7748237 1.6733193
 15.0  5.600E − 09   3.353E − 09   5.371E − 09   3.232E − 09  1.7748246 1.6733198
 20.0  6.900E − 09   3.976E − 09   6.601E − 09   2.821E − 09  1.7748260 1.6733205
 25.0  2.992E − 08   4.345E − 08   2.668E − 08   4.097E − 08  1.7748285 1.6733212
 30.0  4.193E − 06   6.322E − 06   3.718E − 06   5.960E − 06  1.7748236 1.6733103
Table 6. Error norms and conserved quantities for v(x, t) and u(x, t).
Time L2 error of v L∞ error of v L2 error of u L∞ error of u I1 I2
IQ            
 0.5  3.598E − 07   4.300E − 07   4.310E − 07   5.425E − 07  1.7748239 1.6733200
 1.0  2.492E − 06   2.925E − 06   3.060E − 06   3.647E − 06  1.7748238 1.6733198
 2.0  1.299E − 05   1.268E − 05   1.510E − 05   1.495E − 05  1.7748235 1.6733196
 3.0  2.101E − 05   1.786E − 05   2.285E − 05   1.978E − 05  1.7748233 1.6733193
 4.0  2.366E − 05   1.894E − 05   2.456E − 05   2.006E − 05  1.7748231 1.6733195
 5.0  3.522E − 05   2.862E − 05   4.034E − 05   3.483E − 05  1.7748232 1.6733192
 10.0  6.753E − 05   4.177E − 05   7.152E − 05   4.450E − 05  1.7748237 1.6733193
 15.0  1.342E − 04   7.717E − 05   1.386E − 04   8.006E − 05  1.7748246 1.6733198
 20.0  1.559E − 04   7.227E − 05   1.600E − 04   7.515E − 05  1.7748260 1.6733205
 25.0  2.088E − 04   8.579E − 05   2.150E − 04   8.807E − 05  1.7748285 1.6733212
 30.0  2.743E − 04   9.665E − 05   2.793E − 04   9.855E − 05  1.7748236 1.6733103
Table 7. Error norms and conserved quantities for v(x, t) and u(x, t).
Time L2 error of v L∞ error of v L2 error of u L∞ error of u I1 I2
IMQ            
 0.5  2.081E − 05   2.670E − 05   2.595E − 05   3.369E − 05  1.7748239 1.6733200
 1.0  9.158E − 05   1.056E − 04   1.114E − 04   1.310E − 04  1.7748238 1.6733198
 2.0  2.616E − 04   2.468E − 04   2.967E − 04   2.830E − 04  1.7748235 1.6733196
 3.0  3.887E − 04   3.171E − 04   4.191E − 04   3.437E − 04  1.7748233 1.6733193
 4.0  4.852E − 04   3.515E − 04   5.094E − 04   3.711E − 04  1.7748231 1.6733195
 5.0  5.616E − 04   3.659E − 04   5.816E − 04   3.815E − 04  1.7748232 1.6733192
 10.0  8.109E − 04   3.712E − 04   8.225E − 04   3.799E − 04  1.7748237 1.6733193
 15.0  1.221E − 03   5.494E − 04   1.253E − 03   5.849E − 04  1.7748246 1.6733198
 20.0  1.783E − 03   6.396E − 04   1.808E − 03   6.490E − 04  1.7748260 1.6733205
 25.0  2.274E − 03   6.435E − 04   2.298E − 03   6.496E − 04  1.7748285 1.6733212
 30.0  2.803E − 03   7.035E − 04   2.835E − 03   7.170E − 04  1.7748236 1.6733103

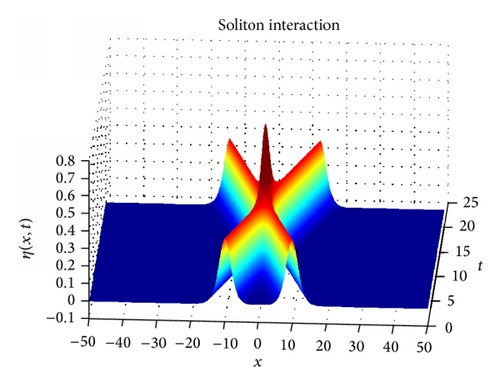
3.3. Problem

In this last example, we present the interaction between two solitons. The initial conditions are taken to be
()
The simulation explored in this section cannot be benchmarked via an exact analytical solution; to the authors knowledge no exact interacting soliton solution is known. However, the results are consistent with known properties of solitary waves [19]:
  • (1)

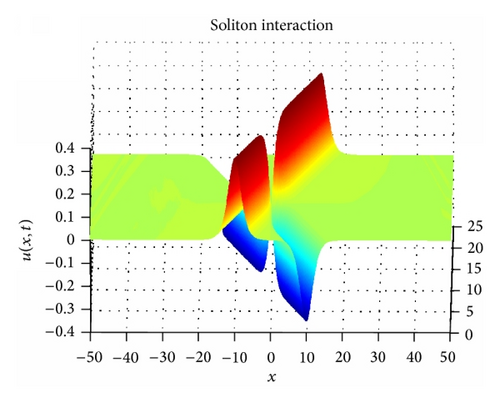
    Solitons are permanent in form.

  • (2)

    Solitons are localized within a region.

  • (3)

    Solitons can interact with other solitons and emerge from the collision unchanged, except for a phase shift.

The simulation is done by using only multiquadratic radial basis functions with 200 node points in x ∈ [−50,50]. The numerical results are shown in Figures 2(a) and 2(b). We can see in both figures that the solitons remain permanent in form except at the time interval of collision. In Figure 3(a) we observe constructive interference of the solitons v(x, t) at t = 8.5. On the other hand, in Figure 3(b) we can see the colliding solitons u(x, t) form destructive interference at t = 8.5. Finally, the figures show that after the collision the solitons emerged unchanged.
Details are in the caption following the image
Figure 3 (a) v(x, t)
Open in figure viewerPowerPoint
Convergence of mesh error.
Details are in the caption following the image
Figure 3 (b) u(x, t)
Open in figure viewerPowerPoint
Convergence of mesh error.

4. Conclusions

We have solved numerically the Boussinesq type system of nonlinear PDE by means of RBFs. In general this algorithm solves the system accurately. In particular, this method has optimal results for multiquadric and Gaussian radial basis functions. The conserved quantities were calculated and show good agreement with the analytical results. In the final section we ran a simulation for interacting solitons that is in agreement with the known properties of solitons. In conclusion the meshless method is shown to give good results for a system of PDEs having high order derivatives and mixed-partial derivatives.

Conflict of Interests

The authors declare that there is no conflict of interests regarding the publication of this paper.

    The full text of this article hosted at iucr.org is unavailable due to technical difficulties.