Chaotic Behavior of One-Dimensional Cellular Automata Rule 24
Abstract
Wolfram divided the 256 elementary cellular automata rules informally into four classes using dynamical concepts like periodicity, stability, and chaos. Rule 24, which is Bernoulli στ-shift rule and is member of Wolfram’s class II, is said to be simple as periodic before. Therefore, it is worthwhile studying dynamical behaviors of four rules, whether they possess chaotic attractors or not. In this paper, the complex dynamical behaviors of rule 24 of one-dimensional cellular automata are investigated from the viewpoint of symbolic dynamics. We find that rule 24 is chaotic in the sense of both Li-Yorke and Devaney on its attractor. Furthermore, we prove that four rules of global equivalence of cellular automata are topologically conjugate. Then, we use diagrams to explain the attractor of rule 24, where characteristic function is used to describe the fact that all points fall into Bernoulli-shift map after two iterations under rule 24.
1. Introduction
Cellular automata (CA) was first introduced by von Neumann in 1951 [1]. CA is a mathematical model consisting of large numbers of simple identical components with local interactions [2]. The simple components act together to produce complex global behavior. CA performs complex computation with high degree of efficiency and robustness. Three major factors have resulted in the revival of interest in the behavior of cellular systems [3]. First, the development of powerful computers and microprocessors has made the rapid simulation of CA possible. Second, the use of CA to simulate physical systems has attracted much interest in the scientific community. Third, the advent of VLSI as an implementation medium has focused attention on the communication requirements of successful hardware algorithms. Therefore, many researches about CA have been reported [4–6], especially in cryptography [7–9] and image processing [10, 11]. In addition, the analysis of dynamical behavior about dynamical system has aroused wide public concern [12–16], such as chaotic behavior [17, 18]. Thus, it is also important to analyze chaotic behavior of CA.
Here, we will only consider Boolean automata for which the cellular state x ∈ {0,1}. A cellular automaton consists of a number of cells which evolve by a simple local rule (identical rule). The value of each cell in the next stage is determined by the values of the cell and its neighbor cells in the current stage under the local rule [19]. The identical rule contained in each cell is essentially a finite state machine (FSM) which is specified in the form of a rule table [20]. A rule table contains an entry for possible neighborhood which consists of a cell and the adjacent cells. The cellular array is d-dimensional, where d = 1,2, 3 is used in practice. In this paper, we will concentrate on d = 1. For a one-dimensional CA, a cell is connected to r local neighbors (cells) on either side, where r is referred to as the radius. A one-dimensional CA has n cells linked in a line or in a circle. Denote the value in the ith cell at the tth stage by xi[t]. For 2-state 3-neighborhood CA (r = 1), the evolution of ith cell can be represented as a function of the present states of (i − 1)th, (i)th, and (i + 1)th. The local function fi is a deterministic function to determine the next-stage value of the ith cell, xi[t + 1] = fi(xi−1[t], xi[t], xi+1[t]). For example, the rule 24 is a one-dimensional CA and its rule table is shown in Table 1. Thus, we have f(000) = 0, f(001) = 0, f(010) = 0, f(011) = 1, f(100) = 1, f(101) = 0, f(110) = 0, and f(111) = 0. Then, we find that the groups of three bits between parentheses represent all the possible neighborhood states and the single bit after equal sign is the resulting output bit at the next time step. The rule number is obtained by multiplying each output bit by the corresponding power of two and adding the results. Therefore, there exist 28 = 256 possible rules with r = 1. In this paper, we mainly discuss rule 24. The rule 24 can be used to extract binary image edges. We know that bit strings 011 and 100 must be detected at the edges of binary images. If every row of an image is evolved according to the rule 24, every column of the image is evolved according to the rule 24 and their results do bitwise XOR (exclusive OR); then the image edges can be obtained. Therefore, it is worth researching the dynamical behaviors of rule 24.
| xi−1xixi+1 | xi−1xixi+1 | ||
|---|---|---|---|
| 000 | 0 | 100 | 1 |
| 001 | 0 | 101 | 0 |
| 010 | 0 | 110 | 0 |
| 011 | 1 | 111 | 0 |
In this paper, complex dynamical behaviors of rule 24 are studied in detail. We obtain two conditions according to Bernoulli στ-shift evolution for attractors under rule 24. The corresponding strongly connected graphs of transition matrices of determinative block systems are given. In terms of strongly connected subgraphs, we can predict the elements of attractor Λ24. Finally, we have proven that rule 24 is chaotic in the sense of Li-York and Devaney on sets of Λ24, which implies that the number of period orbits of rule 24 is infinite.
The rest of the paper is organized as follows. In Section 2, the intent of the paper and notations of symbolic dynamics are introduced. In Section 3, the dynamical behaviors of rule 24 are studied. In Section 4, we prove that four rules of global equivalence are topologically conjugate. In Section 5, characteristic function is used to describe the fact that all points fall into Bernoulli-shift map after two iterations under rule 24 and Lameray diagram is used to show clearly the iterative process of an attractor. Section 6 presents some conclusions.
2. Preliminaries
In 1980s, Wolfram proposed CA as models for physical systems which exhibit complex or even chaotic behaviors based on empirical observations, and he divided the 256 elementary cellular automata (ECA) rules informally into four classes using dynamical concepts like periodicity, stability, and chaos [21–23]. However, some authors [24–28] found that some rules of Bernoulli στ-shift rules are chaotic in the sense of both Li-York and Devaney, where these rules were said to be simple as periodic by Wolfram. Rule 24 is belonging to Bernoulli στ-shift rules. Therefore, we need to research rule 24 and to find its some new dynamical properties.
In this paper, we will use some notations about CA as follows.
Chua et al. [29] mentioned that each rule has three globally equivalent local rules determined by three corresponding global transformations, namely, left-right transformation T†, global complementation , and left-right complementation T*. Each equivalence class is identified by , where κ is complexity index and m is index of κth class. In [30], the authors presented that 112 rules of 256 local rules were Bernoulli στ-shift rules. Each of the 112 Bernoulli στ-shift rules has an ID code BN[α, β, τ], where α denotes the number of attractors of rule N, β denotes the slope of the Bernoulli στ-shift map, and τ denotes the relevant forward time-τ. Hence, the space-time evolution of any one of the 112 rules on their attractors can be uniquely predicted by two parameters: β = ±2σ and τ. For example, the attractors of rule 14 are (β = −1/2, σ = −1, τ = 1) and (β = 2, σ = 1, τ = 1).
Some notations about symbolic dynamics can be referred to in [24–27]
3. Dynamical Behaviors of f24
In the section, we investigate the complexity and chaotic dynamics of f24. In order to give our results, some definitions need be introduced.
Definition 1 (see [32].)A square {0,1} matrix A is irreducible, if for every pair of indices i and j there is an n such that .
Definition 2 (see [32].)A square {0,1} matrix A is aperiodic, if there exists N, such that , n > N, for all i, j.
Definition 3 (see [32].)Suppose that g : X → Y is a continuous mapping, where X is a compact topological space. g is said to be topologically mixing if, for any two open sets, U, V ⊂ X, ∃N > 0, such that gn(U)∩V ≠ ∅, for all n ≥ N.
Definition 4 (see [26].)Let (X, f) and (Y, g) be compact spaces; we say f and g are topologically conjugate if there is a homeomorphism h : X → Y, such that h∘f = g∘h.
We give conditions according to Bernoulli στ-shift evolution for rule 24 as follows.
Theorem 5. For rule 24, there exists a subset Λ24 ⊂ SZ which satisfies if and only if, for all x = (…, x−1, x0, x1, …) ∈ Λ24, xi−1, xi, and xi+1 have the following relations.
- (i)
If xi = 0, then xi−1 = 0, xi+1 = 0; xi−1 = 0, xi+1 = 1, xi+2 = 1; xi−2 = 0, xi−1 = 1, xi+1 = 0.
- (ii)
If xi = 1, then xi−2 = 0, xi−1 = 0, xi+1 = 0, xi+2 = 0.
Proof. Necessity: suppose that there exists a subset Λ24 ∈ SZ such that . Then for all x = (…, x−1, x0, x1, …) ∈ Λ24, we have , for all x ∈ Z.
- (i)
If xi = 0, then ; according to Table 1, we get xi−1 = 0, xi+1 = 0; xi−1 = 0, xi+1 = 1, xi+2 = 1; xi−2 = 0, xi−1 = 1, xi+1 = 0.
- (ii)
If xi = 1, then ; according to Table 1, we get xi−2 = 0, xi−1 = 0, xi+1 = 0, xi+2 = 0.
Sufficiency: suppose that there exists a subset Λ24 ⊂ SZ and, for all x ∈ Λ24, the relations between xi−1, xi and xi+1 satisfy the conditions (i) and (ii) in Theorem 5, for all i ∈ Z.
- (i)
If xi = 0, we have .
Therefore,
- (ii)
If xi = 1, we have
()
Hence, .
Remark 6. From the definition of subsystem, we know that (Λ24, f24) are subsystems of (SZ, f24).
The dynamical behaviors of f24(x) on the set Λ24 are shown as follows.
Let P = {r0, r1, r2, r3} be a new state set, where r0 = (000), r1 = (001), r2 = (010), r3 = (100), and ϖ24 = { (rr′)∣r = (b0b1b2), , ∀1 ≤ j ≤ 2 such that . Furthermore, subshift of ς is defined as . The transition matrix B24 of the is
Obviously, B24 is a square {0,1} matrix. A square {0,1} matrix corresponds to a directed graph. The vertices of the graph are the indices for the rows and columns of B24. There is an edge from vertex i to vertex j if . A square {0,1} matrix is irreducible if and only if the corresponding graph is strongly connected. If ΛA is a two-order subshift of finite type, then it is topologically mixing if and only if A is irreducible and aperiodic.
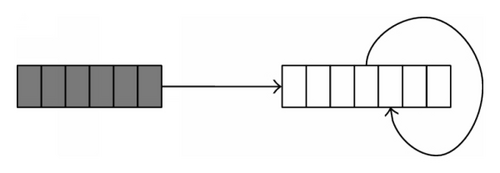
We give corresponding graph G24 of the matrix B24 in Figure 1, where vertices are the elements of set P. It is obvious that G24 is a strongly connected graph.
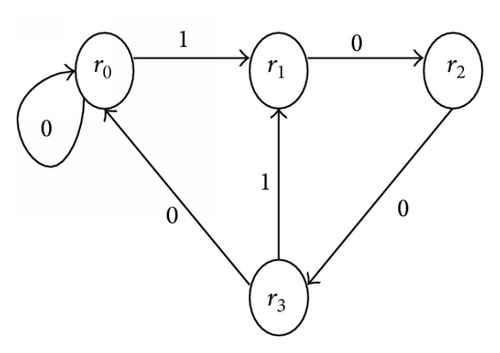
Remark 7. By definition, we know that P is the determinative block system of Λ24 and is a subshift of finite type.
Remark 8. Carefully observing Figure 1, we find that there are several strongly connected subgraphs: r0 → r0, r1 → r2 → r3 → r1, r0 → r1 → r2 → r3 → r0. The elements of will be composed by all vertices of subgraphs, respectively. For example, and x1 is composed of vertices of subgraph r1 → r2 → r3 → r1; then we have r0⊀x1 and vertices of subgraph r1 → r2 → r3 will appear in x1, if |x1| = 3k, k = 1,2….
Remark 9. Let e1 = (011), e2 = (101), e3 = (110), and e4 = (111). In terms of Table 1, we find that, after one iteration, the possible sequences are generated by e1, e2, e3, and e4 as follows:
-
e1 → 010, e2 → 000 or 001, e3 → 000, 001, 100 or 101, e4 → 000 or 100.
Theorem 10. is global attractor of f24.
Proof. To prove that is the global attractor of f24, we consider two situations.
- (i)
. Since is invariant under f24, we have .
- (ii)
. Suppose that there exist such that f24(x) = y. Then, we have (011)≺y, (101)≺y, (110)≺y, or (111)≺y by Theorem 5. Without loss of generality, we consider several situations as follows.
- (a)
Let y[−1,1] = (011). Since , for all i ∈ Z, we especially have
()()()
- (a)
-
- (b)
Let y[−1,1] = (101). Since , for all i ∈ Z, we especially have
()()()
- (b)
Therefore, it follows from Table 1 that x[−2,0] ∈ {(011), (100)} by (9). Furthermore, if x[−2,0] = (011), we know that y[−i,i] = (…, 0,1, 1, …) is no ancestor. If x[−2,0] = (100), then only (011) satisfies (11). However, we know that y[−i,i] = (…, 0,1, 1, …) is no ancestor. The situations of (110) and (111) are similar to those of (011) or (101). In conclusion, if , x will be no ancestor or its ancestor will be no ancestor. Therefore, is global attractor of f24.
Remark 11. From the above conclusion, we find that all binary sequences will be bound to fall into after two iterations under f24.
Based on the above definitions and analysis, we have the following results.
Theorem 12. (a) and are topologically conjugate.
(b) is topologically mixing.
(c) is topologically mixing.
(d) The topological entropy .
Proof. (a) We find out a homeomorphism h from to .
Define
(b) Since and are topologically conjugate, we only need to check that the transition matrix B24 of is irreducible and aperiodic. Actually, , for all n ≥ 5. By Definitions 1 and 2, we know that B24 is irreducible and aperiodic. So, in terms of [32, 33], is topologically mixing.
(c) Since f24(x) and ς(x) are equal in the set and is topologically mixing, is topologically mixing.
(d) The topological entropy ς on equals logρ(B24), where ρ(B24) is the spectral radius of the transition matrix B24 of the subshift . So, . Because two topological conjugate systems have the same topological entropy, the topological entropy of is equal to that of ; namely, .
Theorem 13. f24 is chaotic in the sense of both Li-Yorke and Devaney on .
Proof. It follows from [33] that the positive topological entropy implies chaos in the sense of Li-Yorke and topologically mixing implies chaos in the sense of Li-Yorke and Devaney, since rule N = 24 possesses very rich and complicated dynamical properties on .
4. The Relationship between Four Rules of Global Equivalence Class
In this section, we will discuss the relationship between four rules of global equivalence class . In [31], rules 24, 66, 231, and 189 are partitioned into global equivalence class . Next, we prove that they are topologically conjugate to each other.
Theorem 14. (i) f24 : SZ → SZ and f66 : SZ → SZ are topologically conjugate.
(ii) f24 : SZ → SZ and f231 : SZ → SZ are topologically conjugate.
(iii) f24 : SZ → SZ and f189 : SZ → SZ are topologically conjugate.
Proof. By [31], we have
Remark 15. If there are two systems topologically conjugate, these two systems have the same dynamical properties. Rules f24, f66, f231, and f189 are topologically conjugate, respectively. Therefore, if we know that one of four rules is chaotic in the sense of both Li-Yorke and Devaney in its attractors, we can deem that the other four rules are chaotic in the sense of both Li-Yorke and Devaney in their attractors, respectively.
5. Using Diagrams to Explain Attractors of Four Rules
We choose I = 14. Figure 2 shows characteristic functions of rule 24. Figures 2(a), 2(b), and 2(c) describe the fact that all points fall into Bernoulli-shift map after two iterations under rule 24, which shows that is global attractor of f24. The phenomenon also shows that the forecast in Remark 11 is correct.
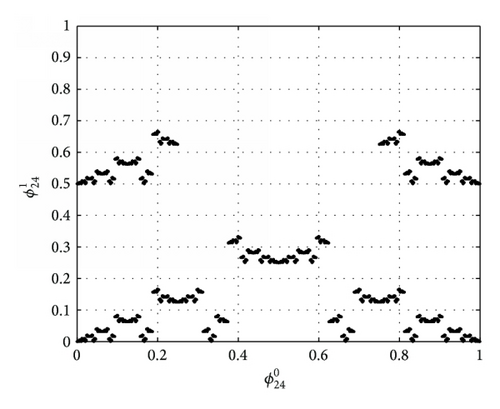
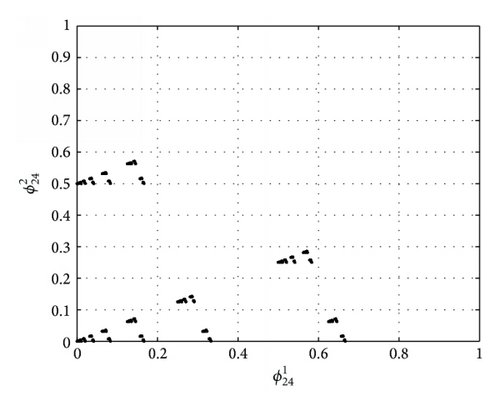
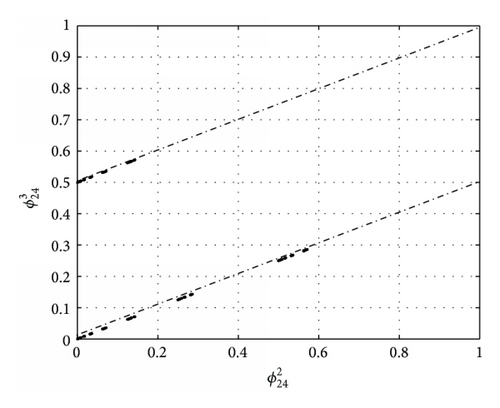
If we choose different values of I for rule 24, we can get different initial binary configurations for the evolution of rule 24. The different initial binary configurations may lead to different attractor periods. If the value of I is fixed, we may find the periods of attractors different. Given I = 5, we find three attractors of rule 24 shown in Figures 3(a), 3(b), and 3(c). Periods of these attractors are 1, 3, and 6, respectively.
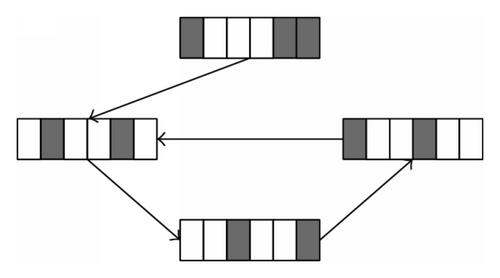
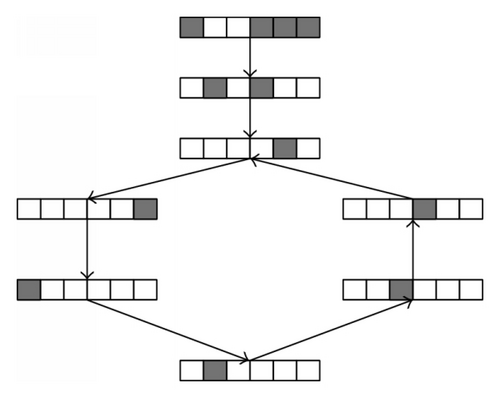
Remark 16. The sequence x = [x0x1 ⋯ xI−1xI] consists of arbitrary alternations of 0 and 1, and there are 2(I+1) different possibilities of choice for x.
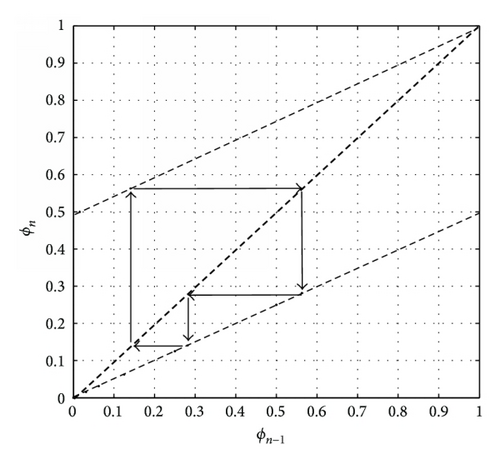
Next, we use Lameray diagram [34] to present the evolution process of attractor. In terms of the attractor of Figure 3(b), we get that the values of characteristic function of the attractor are 0.2813, 0.1406, and 0.5625, respectively. Figure 4 shows the iterative process of the attractor. Then, we can associate the period-3 attractor of rule 24 as a period-3 point of a continuous map f : [0,1]→[0,1] which we know to be chaotic because “period-3 implies chaos” [35].
6. Conclusion
In this work, we characterize the global attractor of rule 24. We derive the conditions according to Bernoulli στ-shift evolution for attractor of rule 24. Then, in terms of the transition matrix of determinative block system of subsystem of rule 24, we obtain the value of topological entropy of subsystem. By corresponding strongly connected graph of transition matrix of determinative block system of subsystem Λ24, we guess that is the global attractor of f24. Furthermore, we prove that is the global attractor of f24. We find that rule 24 is topologically mixing on . Then, we prove that four rules of global equivalence of ECA are topologically conjugate. So, these four rules are chaotic in the sense of both Li-Yorke and Devaney on their attractors, respectively. We use diagrams to explain the attractor of rule 24, where characteristic function and Lameray diagram are used to describe the fact that all points fall into Bernoulli-shift map after two iterations and to show clearly the iterative process of an attractor, respectively.
Conflict of Interests
The authors declare that there is no conflict of interests regarding the publication of this paper.
Acknowledgments
This work was supported in part by the Research Project of Chongqing University of Science and Technology (CK2013B15), Scientific and Technological Research Program of Chongqing Municipal Education Commission (KJ131401, KJ131416), the Natural Science Foundation Project of CQCSTC (cstc2012jjB0095), the National Natural Science Foundation of China (51275547), and Achievement Transfer Program of Institutions of Higher Education in Chongqing (KJ121413).




