Parameters Separated Calibration Based on Particle Swarm Optimization for a Camera and a Laser-Rangefinder Information Fusion
Abstract
Heterogeneous sensors fusion of a camera and a laser-rangefinder can greatly improve the environment perception ability, and its primary problem is the calibration of depth scan and image information. At first, the mapping relationship among world coordinate system, camera coordinate system, and image plane is discussed, and then the calibration of camera intrinsic parameters is achieved. Moreover, the intrinsic and extrinsic parameters separated calibration is presented for a camera and a laser-rangefinder, and the characteristic identification is adopted by two intersection calibration boards with a certain angel for fusion characters extraction. Furthermore, the particle swarm optimization is proposed for the extrinsic parameters estimation with different objectives, and the Gaussian elimination is utilized for the initial particle swarm. The simulation and real experimental results show that the standard deviation of calibration error in the 21-group experiments is decreased by 10.175%, and it also proves the accuracy and effectiveness of our approaches.
1. Introduction
The ability of environmental perception has been considered as an important functionality for heterogeneous multisensor system [1]; heterogeneous sensors system usually includes camera and laser range finders, which are applied to compensate for their drawbacks of each sensor in order to be more reliable. Among those sensors, a camera has been the most popular sensor for recognizing objects, but the camera is too sensitive to the light and the weather and has some limits to acquire depth information, while the laser range finders can give more accurate depth information [2]. Meanwhile, they are also used as the main sensor for autonomous navigation [3]. Therefore, a laser- rangefinder and a camera have different abilities to capture the surrounding information, if these abilities of the two sensors are combined to improve the environment perception ability for multisensor system. However, one of the major problems for heterogeneous sensors fusion is to match the data from these different sensors [4]. The information fusion of two sensors requires knowing in advance the relative pose between the camera and the laser-rangefinder. Thus our paper addresses the intrinsic parameters and extrinsic parameters separated calibration, and then the extrinsic parameters are estimated by the particle swarm optimization (PSO) to decrease the calibration error.
The number of published works on the intrinsic and extrinsic parameters separated calibration of a camera and laser-rangefinder is relatively little. Meanwhile, the particle swarm algorithm that is adopted to optimize the extrinsic parameters in this paper is also novel. As we all knew that the most classic calibration method was proposed by Zhang and Pless [5], it described a practical procedure where a check board pattern was freely moved in front of the two sensors; it was one of the successful and valid algorithms, so we utilized a part of Zhang’s algorithm for intrinsic parameters calibration in this paper. As for the extrinsic parameters calibration, it was achieved by freely moving a check board pattern in order to obtain plane poses in camera coordinates and depth information in the LRF reference frame [6]. Meanwhile, an external parameter calibration method for multiple cameras with nonoverlapping fields of view using a laser-rangefinder (LRF) was presented in [7]. And a modular approach had been extensively tested during VIAC which had offered a unique chance to face pros and cons of different calibration procedures in [8]. Furthermore, the original nonlinear calibration model of multiple LIDARs was reformulated as a second-order cone program (SOCP) on a mobile vehicle platform in [9], the nonlinear distortion of the camera was considered, and the calibration parameters were determined with the least square error in [10]. However, the intrinsic parameters and extrinsic parameters mixed as a kind of parameters matrix to calibrate at the same time, which led the space of solution to become larger; meanwhile, the errors of parameters estimation are increased. Therefore, the camera’s intrinsic parameters and extrinsic parameters were separated in order to improve the accuracy of calibration [11]; nonlinear least square and nonlinear Gauss-Newton method are utilized to optimize parameters. However, the performance of parameters optimization is limited by the algorithm. Furthermore, a novel laser-rangefinder calibration method was proposed by using genetic algorithm to overcome the problem [12] that the conventional camera calibration methods cannot correct the misalignment of this rangefinder. The fitness function estimated the difference between the actual image outputs and the calculated image outputs. Therefore, we proposed particle swarm optimization (PSO) to optimize the extrinsic parameters for heterogeneous sensors calibration of laser-rangefinder and camera in this paper; at the same time, the Gaussian elimination is utilized to initialize the particle swarm, and we improve the fitness function according to decreasing the calibration error. Therefore, not only is it effective in calibrating the separated parameters based on PSO, but also it can decrease the error of calibration.
The rest of paper is organized as follows. Section 2 describes the coordinate transformations from laser-rangefinder to optical image plane. In Section 3, we introduce how to calibrate the intrinsic parameters and the extrinsic parameters separated calibration method. Then the extrinsic parameters estimation and optimization based on PSO are designed in Section 4. Section 5 exhibits some comparison experimental analysis of the laser-rangefinder and the camera fusion calibration based on PSO. At last, Section 6 provides the conclusion for this paper.
2. Coordinate Transformations from Laser-Rangefinder to Optical Image Plane
The hardware of information fusion platform mainly consists of a laser-rangefinder and a camera. Here the type of laser-rangefinder is SICK LMS291 [13], which is noncontact measurement systems, and scans their surroundings two-dimensionally. We select horizontal angle field of 180°, the interval angle is 1°, and transmission rate is set as 500 Kbps. The data structure of laser-rangefinder is a kind of 1 × 181 dimensional matrix array, so a median filter is utilized to remove the noise data. Moreover, the camera is FFMV-03MTC-CS, using 1394 transmission mode and its resolution of 640*480, because the camera of IEEE 1394 bus can be satisfied for the demand of real time.
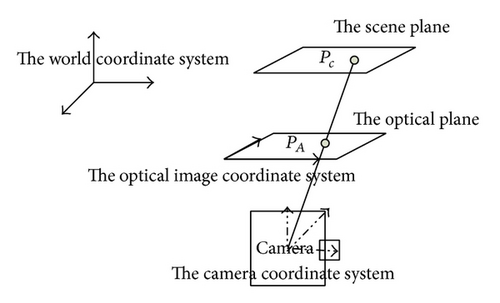
The observed objects captured by laser-rangefinder are distance information of a depth plane in the space, while the objects collected by camera are optical information according to the optical principle. Due to the heterogeneity of data acquisition, the images of camera and the datum of laser- rangefinder are heterogeneous. Hence, it is significant to integrate those heterogeneous data into the same coordinate system for information fusion. Therefore, there are two main steps to map laser- rangefinder information to optical images plane through coordinate transformation [14]. Firstly, we need to obtain a relatively accurate transformation matrix according to ideal physical model, which can ensure data captured by laser-rangefinder mapping into optical image coordinate system. Secondly, since image coordinates of each pixel are discrete, it is necessary to utilize gray-scale interpolation method for each coordinate transformation after spatial coordinate mapping, which can make them fall on the exact pixel points even when the coordinates of four surrounding points are not integer.
2.1. Spatial Coordinate Transformation
2.2. Gray-Scale Interpolation for Information Fusion
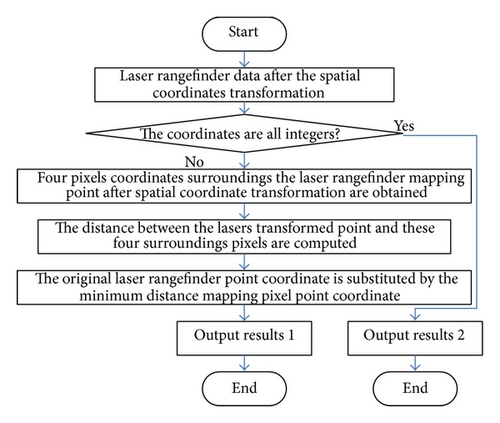
Since the coordinates of each pixel are discrete, it may fall on the noninteger pixel after coordinate transformation. The interpolation method is needed to use after each coordinate transformation in order to fall on the exact pixel points. Hence, we use neighbor interpolation method to realize gray- scale interpolation, as is depicted in Figure 1. Here, if the laser-rangefinder transformed coordinates are not integers, the four-pixel coordinates that are surrounding the laser-rangefinder mapping point after spatial coordinate transformations are captured firstly. Secondly, the distance between the lasers mapping point and these four surrounding pixels is computed. Thirdly, the original laser-rangefinder point coordinate is substituted by the minimum distance mapping pixel point coordinate.
2.3. The Calibration Parameters Analysis
The camera parameters are classified into the intrinsic parameters and extrinsic parameters. Generally, the inherent characteristics and properties of the camera are determined by its intrinsic parameters, since they are not going to change for the same camera. In other words, for a camera, if the focal length or the mechanical structure keeps invariability, its intrinsic parameters are fixed. However, the extrinsic parameters represent the pose and orientation information of the camera in the world coordinate system. Therefore, the extrinsic parameters can be denoted by the orthonormal rotation matrix and translation vector. Wherefore, it is necessary to measure intrinsic parameters and extrinsic parameters of the camera separately; especially when position and orientation of the target objects are restored from the optical image to spatial coordinate, the process is called calibration for a camera and a laser-rangefinder. Thus intrinsic and extrinsic parameters of the camera are indispensable for data fusion [16].
3. The Calibration and Analysis of Camera Intrinsic Parameters

4. Extrinsic Parameters Separated Calibration Estimation Method

According to (13), the separated calibration of intrinsic and extrinsic parameters are required to solve these 13 unknown parameters (fu, fv, u0, v0, w11, w12, w13, w21, w22, w23, t1, t2, t3). By above analysis, we can gain w31 = w32 = w33 = 0 according to (10) here, fu, fv, u0, and v0 are the intrinsic parameters, which are gained from (8). So only w11, w12, w13, w21, w22, w23, t1, t2, and t3 extrinsic parameters are left to be estimated.
4.1. The Characteristic Parameters (A, B, xt, yt) Identification
Additionally, (A, B, xt, yt) are also seen as the known parameters in (13), because they can be calculated by characteristic line and characteristic points on the separating intersection line as (12). Here, we identify those characteristic parameters through any two characteristic points, which are extracted on the characteristic line of Au + Bv = 1, so A and B characteristic parameters can be determined. Meanwhile, as for laser-rangefinder data, (xt, yt) are considered as the maximum curvature points in the intersection line of scanning plane and calibration plate, which need to fall in the line Au + Bv = 1. Therefore, the maximum curvature object point is extracted from a series of points on the intersection with calibration plate; then (xt, yt) are gained.
Moreover, lots of experimental data are needed to substitute into (13) to solve and estimate the other parameters. These various effective experimental data are obtained by altering relative pose between the objects and camera under different experimental surroundings, for instance, changing the inclination of the object or adjusting the distance between the object and the camera. Significantly, it has to be guaranteed that laser-rangefinder and optical image data are collected synchronously.
4.2. Extrinsic Parameters Separated Calibration Based on Particle Swarm Optimization
In fact, w11, w12, w13, w21, w22, w23, t1, t2, and t3 extrinsic parameters can be estimated by 9 equations from (13) which are designed by 9 different scene experiments after the fu, fv, u0, and v0 and A, B, xt, and yt are all solved. As we all know that Gaussian elimination (also known as row reduction) is an algorithm for solving systems of those linear equations, in this paper, Gaussian elimination is utilized to choose proper initial solution for the particle swarm. However, the initial solution is not the best solution to estimate the extrinsic parameters which may bring into lots of calibration error. Therefore, it is beneficial for the particle swarm optimization algorithm to improve extrinsic parameters estimation performance.
-
Algorithm 1: The summary of the PSO algorithm.
-
(1) Initialize.
-
(1.1) Generate an initial swarm of N particles at random by Gaussian elimination.
-
(1.2) Generate initial velocities vid, 1 ≤ i ≤ N and 1 ≤ d ≤ D, at random.
-
(2) Repeat until a given maximal number of iterations is achieved.
-
(2.1) Evaluate the fitness of each particle using (20).
-
(2.2) Determine the best vector pbest visited so far by each particle.
-
(2.3) Determine the best vector gbest visited so far by the whole swarm.
-
(2.4) Update velocities vid using (18) according to the factor model.
-
(2.5) Update particle vectors xid using (19).
5. Data Fusion Experiment Analysis for the Calibration of Laser- Rangefinder and Camera
5.1. Extraction Characteristic Parameters A, B of Au + Bv = 1
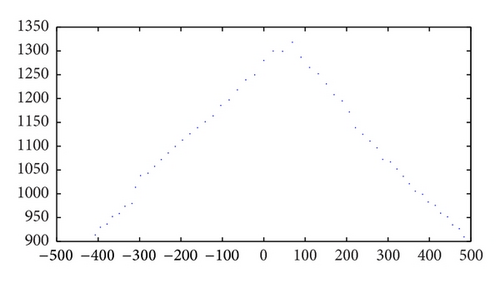
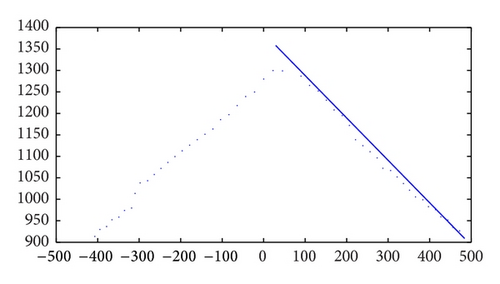
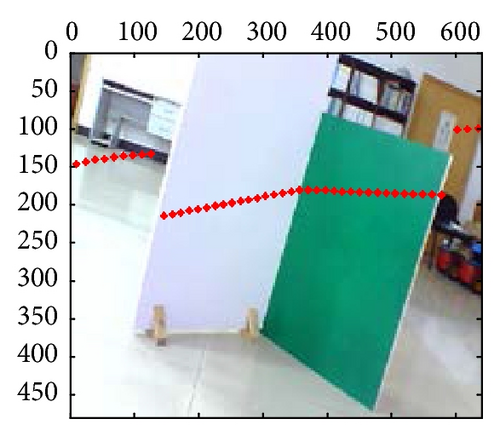
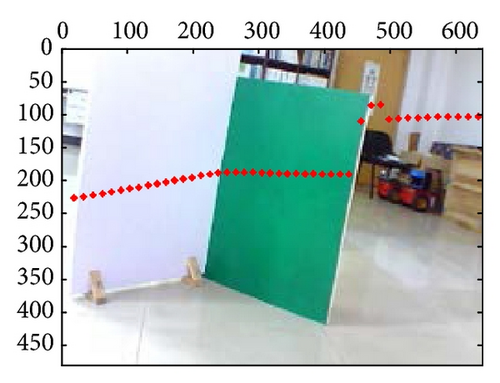
According to the characteristic line Au + Bv = 1 of camera images, which is the intersection line of two calibration boards shown in Figure 4, the characteristic line is able to be extracted through selecting any two points manually, which are not the same points on the image, and those two points can determine the characteristic line; then the characteristic parameters of A, B can be calculated.
5.2. Feature Point Pt(xt, yt) Extraction Based on Laser-Rangefinder
Before extracting feature point Pt(xt, yt), the observational data in the intersection line of laser- rangefinder scanning plane and calibration plate are needed to collect firstly. Moreover, the laser-rangefinder data of calibration board should be shown as “arrow” pattern, because the pattern can be set manually. Furthermore, the two edges straight lines of the arrow-shaped pattern are extracted; then the intersection of the two straight lines can be calculated to obtain Pt(xt, yt). As is shown in Figure 5, the two-line intersection is the object feature point Pt(xt, yt).

5.3. PSO for the Extrinsic Parameters Separated Calibration and Optimization
| Order | s | w11 | w12 | w13 | w21 | w22 | w23 | t1 | t2 | t3 | Time (s) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0.3244 | 5.3536 | −0.1320 | −0.2327 | 1.0309 | −0.6892 | −5.3457 | 2.7222 | −109.3953 | 5.3276 | 0.7237 |
| 2 | 0.3404 | 2.5309 | −0.0624 | −0.2304 | 0.4784 | −0.2557 | −2.5310 | 1.3692 | −55.4788 | −7.1949 | 0.7175 |
| 3 | 0.3328 | 1.6392 | −0.0385 | −0.0641 | 0.3289 | −0.2452 | −1.5627 | 0.5244 | −37.1193 | −12.9526 | 0.7059 |
| 4 | 0.3291 | −12.4868 | 0.3137 | 0.7653 | −2.3754 | 1.7716 | 12.2181 | −5.2497 | 241.8434 | 16.5697 | 0.7237 |
| 5 | 0.3432 | − 17.5503 | 0.4231 | 1.6248 | −3.2606 | 2.3388 | 17.1477 | −1.6669 | 323.7501 | −4.5083 | 0.7253 |
| 6 | 0.3726 | −29.0181 | 0.6558 | 3.8494 | −5.3153 | 7.3192 | 28.4911 | 1.9166 | 525.3508 | −44.1139 | 0.7117 |
| 7 | 0.3476 | −37.5951 | 0.9284 | 3.0366 | −7.1762 | 6.2046 | 36.1728 | −15.2600 | 730.2179 | 199.5670 | 0.7062 |
| 8 | 0.3694 | −1.6929 | 0.0415 | 0.1844 | −0.3119 | 0.1704 | 1.6258 | −0.5066 | 30.9968 | 10.4553 | 0.7103 |
| 9 | 0.3232 | −5.0241 | 0.1244 | 0.3380 | −0.9736 | 0.4936 | 4.8326 | −1.7687 | 101.7259 | 27.9931 | 0.7144 |
| 10 | 0.2981 | −1.3242 | 0.0331 | 0.0620 | −0.2632 | 0.1257 | 1.2699 | −0.6325 | 29.2756 | 9.3599 | 0.7153 |
| Average | 0.3381 | 0.7154 | |||||||||
| In [11] | 0.3764 | −2.5745 | 0.0604 | 0.0418 | −0.4989 | 0.3808 | 2.5037 | −0.3860 | 53.7654 | 5.2954 | 0.4966 |
However, the computational cost of particle swarm optimization algorithm is a little heavier than the methods in [11]; certainly, it also meets the requirements for the calibration reliability and real-time. As we all know that the intrinsic parameters are related to the inherent attribute of camera closely, the extrinsic parameters reflect the relative direction and position between the laser-rangefinder and the camera. After intrinsic and extrinsic parameters are calibrated, the sensor fusion process will not change those parameters. In other words, only if the camera is the same camera, the relative direction and position between laser-rangefinder and camera keep unchanged; then those calibration parameters also remain unchanged. Thus, we understand that the performance of calibration real time is not so significant as the performance of calibration accuracy for the calibration because we can calibrate parameters offline before the sensor fusion. In Table 1, the running time of 0.7154 s could be accepted by the sensor fusion process. Meanwhile, the optimization extrinsic parameters of each different experiment are all list in Table 1.
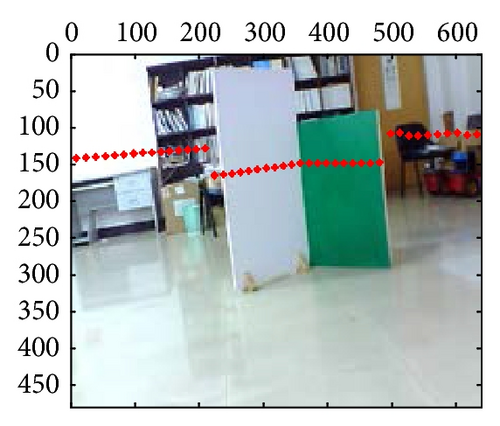
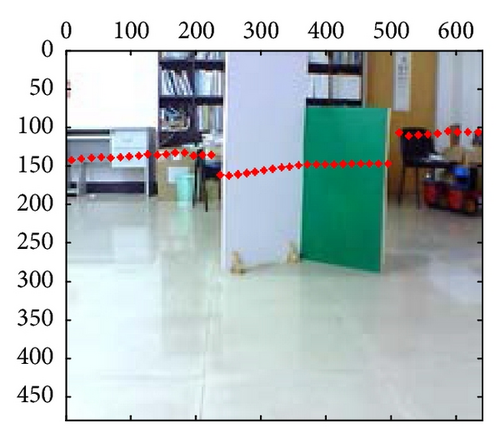
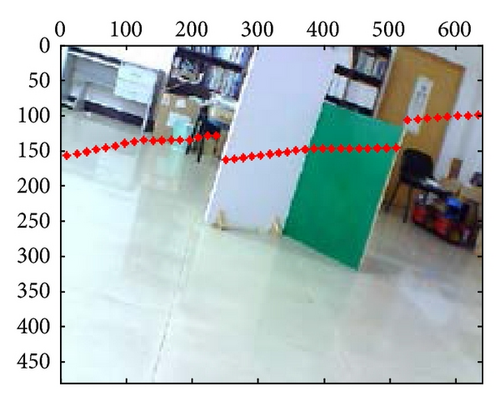
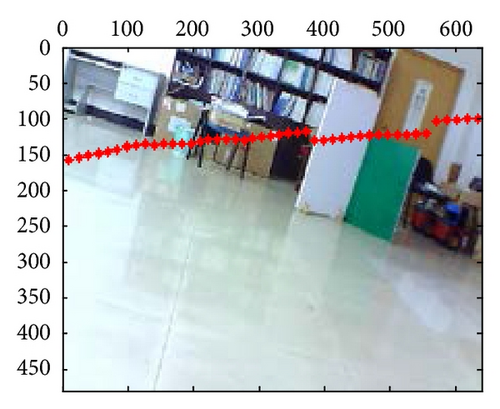
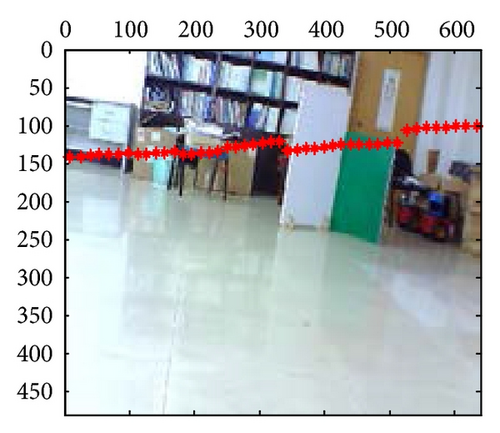
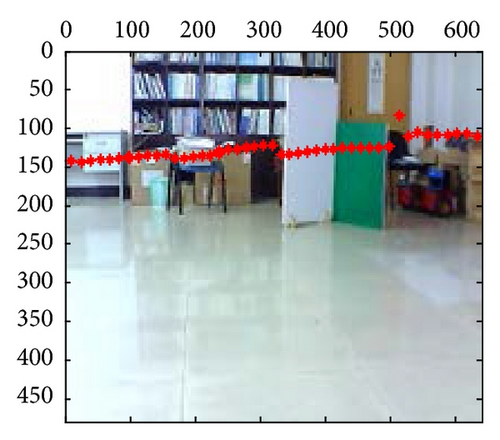
These mixed and separated intrinsic and extrinsic parameters are compared, respectively, for the laser-rangefinder and the camera data fusion. Figure 6 includes three examples of intrinsic and extrinsic parameters mixed method, which shows the apparent deviation errors in the black panes; however, parameters separated method leads to fewer errors, as shown in Figure 7. Meanwhile, the mapping effects of laser-rangefinder points onto the image are more reasonable with actual situation in Figure 7.


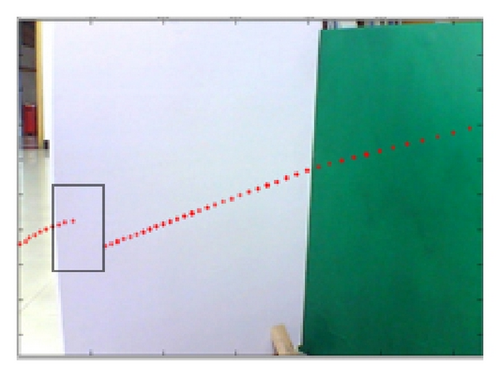
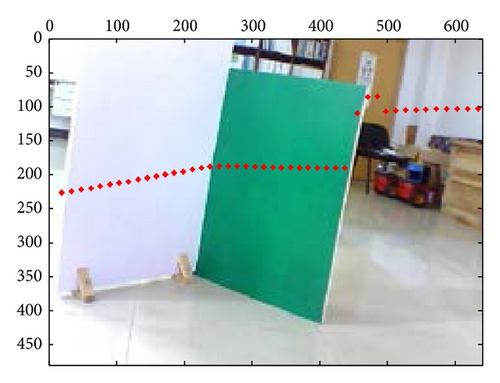
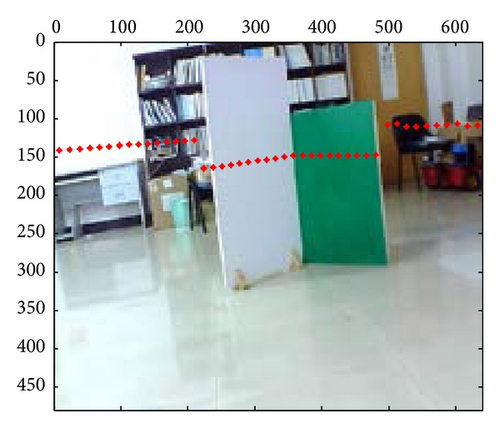
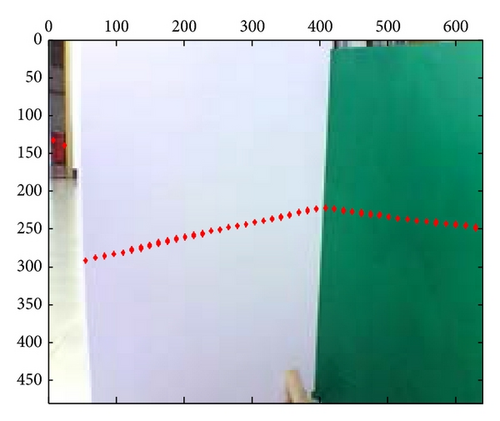
Additionally, the convergence curve for PSO to optimize the extrinsic parameters in the 10th experiment is given; we conclude that the standard deviation of the 21-group is always decreasing with iteration time increasing according to Figure 8. At last, it converges to 0.2981, which is much lower than the standard deviation from the methods in [11].
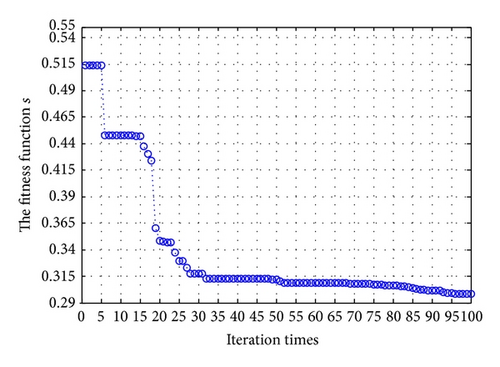
Furthermore, the best PSO calibration result of the tenth experiment is 0.2981, which is better than 0.3764. From the performance comparison between the PSO and the method in [11] for the optimization extrinsic parameters, we find that the majority of experiments by PSO for the optimization extrinsic parameters are better than the method in [11], except the 5th, 9th, 10th, 12th, and 15th experiment scene, as is shown in Figure 9, but the total standard deviation 0.2981 of PSO for extrinsic parameters calibration is better than 0.3764 of the method in [11], and the standard deviation of calibration error in the 21-group experiments is decreased by 10.175% compared with the method in [11].
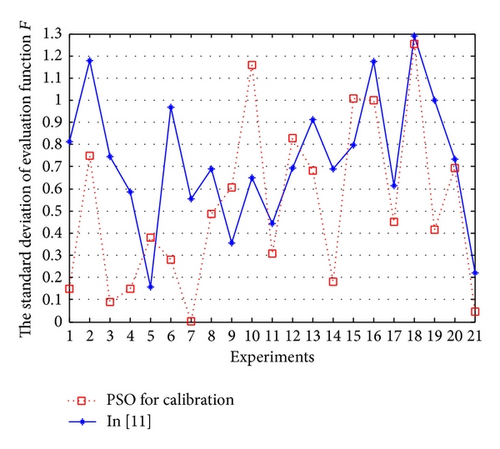
Extrinsic parameters optimization is achieved by PSO; it considers two optimization objectives; the multiobjective calibration process is translated into a comprehensive objective. While the nonlinear least square is utilized for the first objective, the nonlinear Gauss-Newton method is utilized for the second objective in [11]; the theoretical evidence is not very sufficient, so the performance of calibration is not better for the sensor fusion.
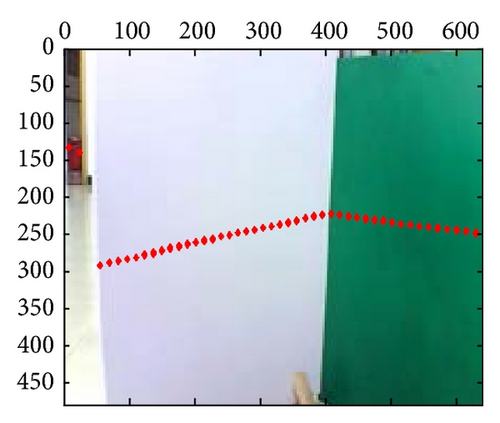
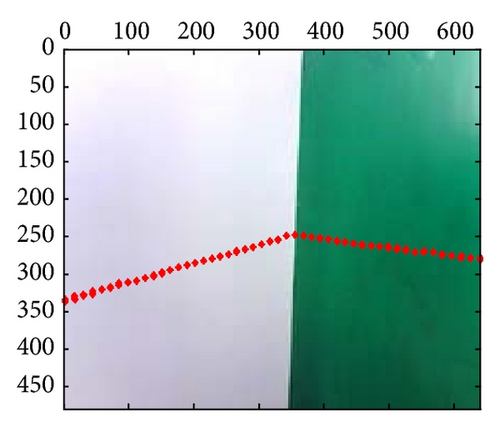
At last, the calibration results for 21-group scene in the 10th independent experiment are shown in Figure 10; from those results, we can confirm that extrinsic parameters calibration based on PSO are valid and effective, especially in their segment boundaries.
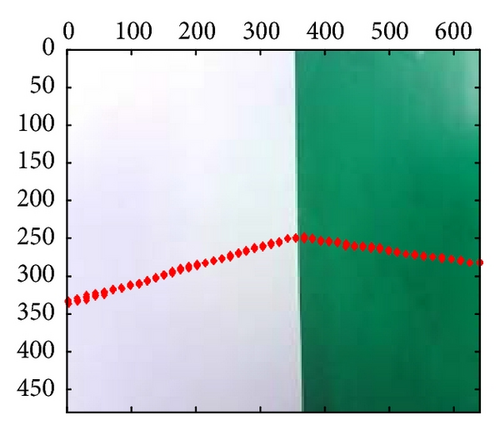
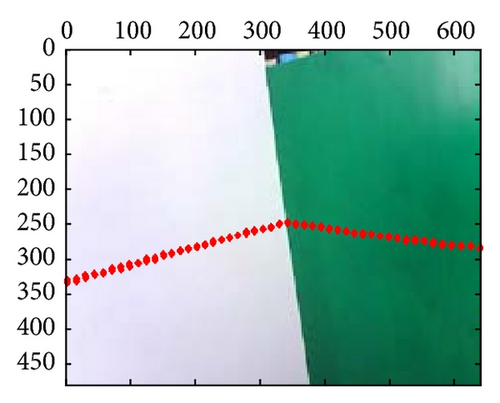
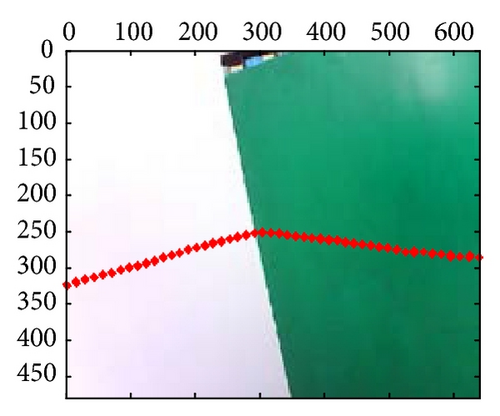
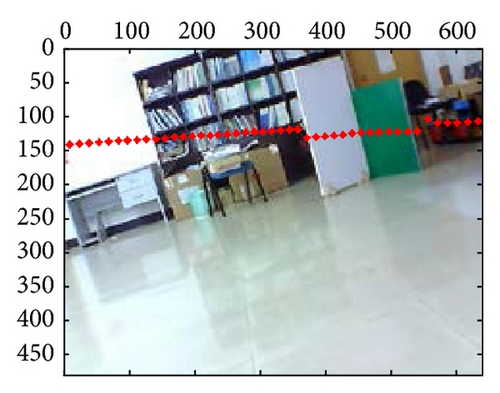
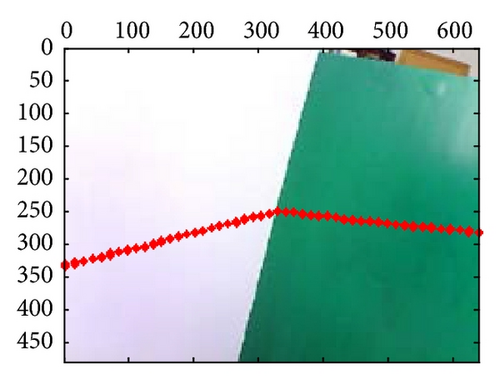
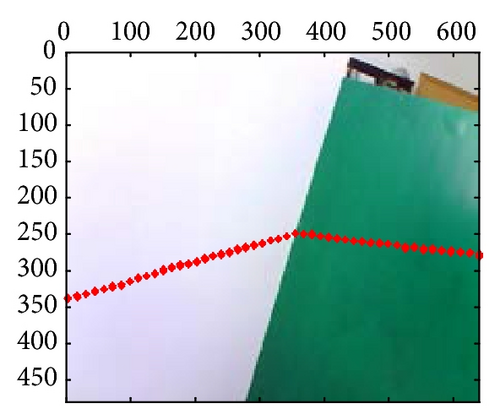
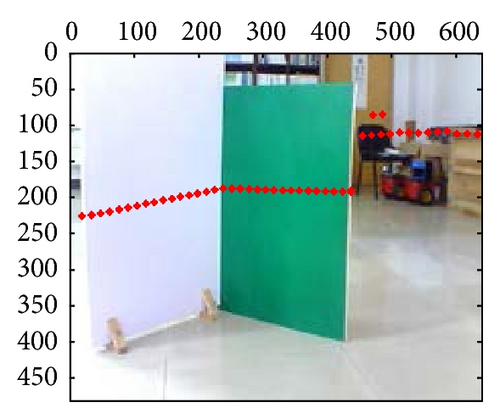
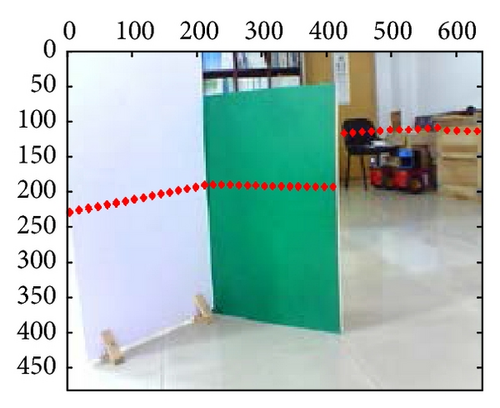
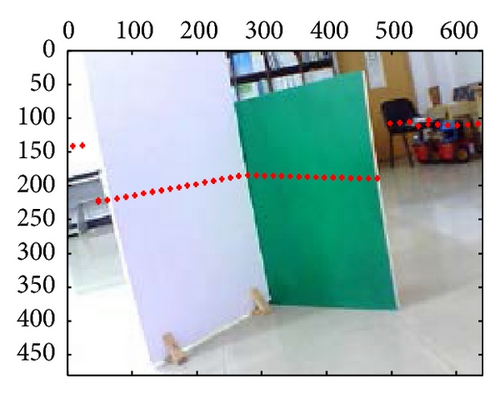
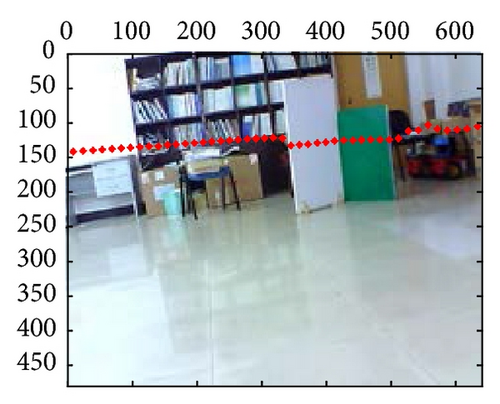

6. Conclusion
According to the principle of heterogeneous calibration and the characteristics of a laser- rangefinder and a camera, the mapping relationship among world coordinate system, camera coordinate system, and image plane is discussed. Meanwhile, calibration algorithm takes into account separated intrinsic parameters and extrinsic parameters. Zhang’s algorithm is adopted to calibrate camera’s intrinsic parameters, and then the inherent properties of camera are analyzed. Moreover, the extrinsic parameters separated calibration and estimation based on PSO are proposed to improve the calibration’s accuracy and validity. Meanwhile, we design a characteristic line method to obtain extrinsic parameters estimation by two intersecting calibration boards with a certain angel. Furthermore, we applied PSO to optimize calibration parameters for two different objectives. And then the availability and reliability of a camera and a laser-rangefinder are insured by the calibration parameters separated and extrinsic parameters optimized based on PSO. In summary, the proposed separated parameters calibration and particle swarm optimization method for the camera and the laser-rangefinder in the paper are an improvement to traditional mixed calibration of intrinsic and extrinsic parameters; meanwhile, both the separated parameters calibration and the extrinsic parameters optimized based on PSO algorithm are to decrease the calibration error; furthermore, the experimental results and analysis indicate that the proposed calibration method can insure the accuracy and reliability of the camera and the laser-rangefinder information fusion.
Conflict of Interests
The authors declare that there is no conflict of interests regarding the publication of this paper.
Acknowledgments
This paper was supported by the National Natural Science Foundation of China (Grant no. 61304253), Natural Science Foundation of Hunan (Grant nos. 13JJ4018 and 13JJ4093), and the Doctoral Program of Higher Education of China (Grant no. 20130162120018).




