Indian Journal of Materials Science
Volume 2014, Issue 1 253018
Research Article
Open Access

Analysis of Free Edge Stresses in Composite Laminates Using Higher Order Theories

Hamidreza Yazdani Sarvestani, 

Corresponding Author

Hamidreza Yazdani Sarvestani

Concordia Center for Composites (CONCOM), Department of Mechanical and Industrial Engineering, Concordia University, 1455 De Maisonneuve Boulevard West, Montreal, QC, Canada H3G 1M8, concordia.ca

Search for more papers by this author
Ali Naghashpour, 

Ali Naghashpour

Concordia Center for Composites (CONCOM), Department of Mechanical and Industrial Engineering, Concordia University, 1455 De Maisonneuve Boulevard West, Montreal, QC, Canada H3G 1M8, concordia.ca

Search for more papers by this author
First published: 04 May 2014
https://doi.org/10.1155/2014/253018
Citations: 3
Academic Editor: S. Raja

Abstract

This paper presents the determination of the interlaminar stresses close to the free edges of general cross-ply composite laminates based on higher order equivalent single-layer theory (HESL). The laminates with finite dimensions were subjected to a bending moment, an axial force, and/or a torque for investigation. Full three-dimensional stresses in the interior and the boundary-layer regions were determined. The computed results were compared with those obtained from Reddy’s layerwise theory. It was found that HESL theory predicts precisely the interlaminar stresses near the free edges of laminates. Besides, high efficiency in terms of computational time is obtainable when HESL theory is used as compared with layerwise theory. Finally, various numerical results were presented for the cross-ply laminates. Also design guidelines were proposed to minimize the edge-effect problems in composite laminates.

1. Introduction

Laminated composite materials are being used in several industries due to their high strength-to-weight ratio and stiffness-to-weight ratio. However, they are susceptible to different types of damage such as delamination which occurs due to high stress concentration near the edge of composite laminates. These stresses are induced by mismatch in elastic properties between adjacent plies of composite laminates [1]. It has been shown that the state of stresses in the edge zone of the laminate is three-dimensional (3D) in nature. Many attempts have been made to compute these stresses next to laminate’s free edges [1–12]. However, because of intrinsic complexities involved in the problem, no exact solution is known for elasticity equations. Therefore, many approximate methods used to determine the interlaminar stresses are recorded in the survey paper by Kant and Swaminathan [3]. Based on a laminated model containing anisotropic layers, the first approximate solution of interlaminar shear stresses was presented by Puppo and Evensen [4]. Other approximate analytical methods used to examine the problem are the employment of the higher order plate theory proposed by Pagano [2], the perturbation technique by Hsu and Herakovich [5], the boundary-layer theory by Tang and Levy [6], and the approximate elasticity solutions by Pipes and Pagano [7]. An approximate theory is also utilized by Pagano [8, 9] based on assumed in-plane stresses and the use of Reissner’s variational principle. The principle of minimum complementary energy and the force balance method are used by Kassapoglou and Lagace [10] to study the symmetric laminates under uniaxial loading. A variational method involving Lekhnitskii’s stress function is utilized by Yin [11, 12] to determine the interlaminar stresses in a multilayer strip of a laminate subjected to combinations of mechanical loads. Lin et al. [13] improved the technique developed by Kassapoglou and Lagace [10] for symmetric laminates under uniaxial tension to evaluate the interlaminar stress distribution near the straight free edges of symmetric and unsymmetric laminates under different types of loading conditions. The first numerical method to solve the 2D governing elasticity equations is given by Pipes and Pagano [1]. They utilized a finite-difference technique to establish the interlaminar stresses in a long symmetric laminate under uniform axial strain. A layer reduction technique and a layerwise theory (LWT) are employed by Lee and Chen [14] in the analysis of a reduced laminate. They neglected the through-thickness stretching and solved a simply supported plate subjected to bidirectional sinusoidal distributed loading. A displacement-based variable kinematic global-local finite element method is offered by Robbins and Reddy [15]. Their displacement field hierarchy contains both a conventional plate expansion (2D) and a full layerwise (3D) expansion. Neves et al. [16, 17] developed a higher order theory that considers deformations in the thickness direction under Carrera’s unified formulation to predict the buckling behaviour of laminated plates and modeling functionally graded plates accounting for extensibility in the thickness direction. The obtained governing equations and boundary conditions are then interpolated by collocation with radial basis functions. Mantari et al. [18] developed a new shear deformation theory for sandwich and composite plates. The presented theory is relatively close to 3D elasticity bending solutions. The theory accounts for adequate distribution of the transverse shear strains through the plate thickness and tangential stress-free boundary conditions on the plate boundary surface; thus, a shear correction factor is not required. A new model is proposed by Rahmani et al. [19] based on the high-order sandwich panel theory to study the effect of external loads on the free vibration of circular cylindrical composite sandwich shells with transversely compliant core, including also the calculation of the buckling loads. Thai et al. [20] present a novel finite element formulation for static, free vibration and buckling analyses of laminated composite plates. The higher order shear deformation plate theory (HSDT) is introduced in the present method to remove the shear correction factors and improve the accuracy of transverse shear stresses. A new improved high-order theory is presented by Kheirikhah et al. [21] for biaxial buckling analysis of sandwich plates with soft orthotropic core. Third-order plate theory is used for face sheets, quadratic and cubic functions which are assumed for transverse and in-plane displacements of the core, respectively.

It was found from the literature that no work has been found to study interlaminar stresses by higher order equivalent single-layer theory (HESL). Here, HESL theory is used to analytically study the interlaminar stresses in both finite and long cross-ply laminates subjected to a bending moment, an axial force, and/or a torque. Then HESL results are compared with those calculated from LWT. The presented works (HESL) are either accurate enough (and general) or computationally efficient.

2. Higher Order Equivalent Single-Layer Theory (HESL)

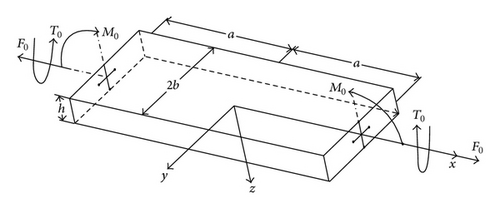
General cross-ply laminates are subjected to the bending moment, the axial force, and/or the torque in order to accurately determine the interlaminar stresses. The geometry of the laminate is illustrated in Figure 1. The formulation is limited to linear elastic material behavior, small strain, and displacements. The coordinate system (x, y, z) is located at the middle plane of the laminate. Thickness, width, and length of the laminate are h, 2b, and 2a, respectively.

Details are in the caption following the image
Figure 1
Open in figure viewerPowerPoint
Laminate geometry and coordinate system.

2.1. Displacement Field and Strains

The integrations of the three-dimensional elasticity strain-displacement relations [22] within the kth layer of the laminate producing the most general form of displacement field are given by
(1a)
(1b)
(1c)
where u1, u2, and u3 represent the displacement components in the x-, y-, and z-directions, respectively, of a material point initially located at (x, y, z) in the undeformed laminate. The displacement field in (1a), (1b), and (1c) may be used, in principle, for obtaining the stress field in any composite laminate subjected to arbitrary combinations of self-equilibrating mechanical and uniform hygrothermal loads. In the present work, however, our attention is focused on symmetric and unsymmetric cross-ply laminates under the bending moment, the axial force, and/or the torque. General cross-ply laminates based on physical grounds can be established as (see Figure 1)
(2)
Upon imposing this condition on (1a), (1b), and (1c), it is readily seen that u(k)(y, z) = 0. Thus, for cross-ply laminates the most general form of the displacement field is given as
(3)
The unknown constants, namely, B1, B2, and B6 appearing in (3), are global response of the laminate. On the other hand, unknown functions v(k)(y, z) and w(k)(y, z) are local response of the laminate.
The purpose of the present section is to show the HESL theory with infinity number of terms which provides sufficiently accurate results for the interlaminar stresses in composite laminate. In HESL, the components of the displacement vector at a material point in cross-ply laminated composite are expressed as [23]
(4)
Relations (4) may more conveniently be presented as
(5)
where k, i, and j are dummy indexes indicating the summation of terms from k = i = j = 1 to desirable number (i.e., l or n or m). It is expected that the accuracy of such theories can, generally, be increased by taking more terms in (5). Also, u1, u2, and u3 are the displacement components of any point within a laminate in the x-, y-, and z-directions, respectively. k + i + j + 3 unknown displacement functions should be found for a single layer or more layers in the laminate. The displacement field in (3) within HESL is simplified by
(6)
By using the displacement field (6) in the principle of minimum total potential energy [22] and considering the constants as unknown parameters, (5 + i + j) equilibrium equations are expressed as
(7a)
(7b)
(7c)
(7d)
(8a)
(8b)
(8c)
where a prime indicates an ordinary differentiation with respect to variable y and the stress and moment resultants appearing in (7a), (7b), (7c), and (7d) and (8a), (8b), and (8c) which are defined as
(9)
By substituting the displacement field (6) into (9), through the linear strain-displacement relations of elasticity and the plane-stress constitutive law [24] of a lamina, the stress and moment resultants can be expressed as
(10a)
(10b)
(10c)
where
(11)
where are the transformed stiffness of an orthotropic lamina. For free edges of the laminate at y = ±b according to the principle of minimum total potential energy the traction-free boundary conditions must be imposed as
(12)
Substituting (10a), (10b), (10c) into (7a), (7b), (7c), the equilibrium equations are obtained in terms of the displacement components which can be given as
(13a)
(13b)
(13c)
(13d)
To determine the parameters B1, B2, and B6 as well as the interlaminar stresses in (13a)–(13d), the general solution of the ordinary differential equations in (13a)–(13d) is first obtained in terms of B1, B2, and B6. Then, by applying the boundary conditions in (12) and using the global equilibrium equation in (8a), (8b), and (8c), the constant parameters B1, B2, and B6 will be found in terms of the bending moment M0, axial force F0, and torque T0. For completeness, the details of the steps involved are displayed in Appendix A.

3. Layerwise Theory

3.1. Displacement Field and Strains

It should be emphasized that the solution proposed by Tahani and Nosier [25] was used to verify HESL theory for predicting stress in the edge of composite laminates. The proposed solution was used while different boundary conditions are considered. This offers to develop new analytical solution which is expressed in the present work. The displacement field in this theory may be represented as [25]
(14)
where u1, u2, and u3 represent the displacement components in the x-, y-, and z-directions, respectively [26]. Also Uk (x, y), Vk (x, y), and Wk (x, y) show the displacement components of all points located on the kth plane in the undeformed laminate, and Φk (z) is continuous function of the thickness coordinate z. Moreover, N indicates the total number of numerical layers considered in a laminate. It should be noted that a repeated index indicates summation over all values of that index. Substituting (14) into the linear strain-displacement relations of elasticity [27], the results are obtained as
(15)

3.2. Equilibrium Equations

Using the principle of minimum total potential energy [23], 3 (N + 1) equations of equilibrium corresponding to 3 (N + 1) unknowns Uk, Vk, and Wk can be shown by
(16)
where k = 1,2, …, N + 1. In (16), the generalized stress and moment resultants are defined as
(17)
The boundary conditions for a laminated plate with a rectangular platform in the layerwise theory at an edge parallel to y-axis involve the specification of Uk or , Vk or , and Wk or . Similarly, at an edge parallel to x-axis, the boundary conditions involve the specification of Uk or , Vk or , and Wk or .

3.3. Displacement Equations of Equilibrium

The linear constitutive relations for the kth orthotropic lamina, with fiber orientations of 0° and 90° only, are given by [24]
(18)
where represent the off-axis stiffnesses within the kth layer of the laminate. By substituting (18) into (17), the stress and moment resultants are written as
(19)
where the coefficients Akj, Bkj, and Dkj appearing in (19) are defined in Appendix B. Finally, substituting (19) into (16) yields the governing equations of equilibrium as
(20)
where a comma followed by a variable indicates differentiation with respect to that variable.

For completeness, the details of the steps involved in the analytical solutions are displayed in Appendix C.

4. Results

4.1. Numerical Results and Discussion

To verify the accuracy and efficiency of the present method, several numerical examples are presented for general cross-ply laminates subjected to the bending moment, axial force, and/or torque. The analyses were performed for 4-layer and 6-layer laminates made of graphite/epoxy. The used mechanical and physical properties of the layers are presented in Table 1 [24].

Table 1. Engineering properties of graphite/epoxy.
Engineering properties E1 (GPa) E2 = E3 (GPa) G12 = G13 (GPa) G23 (GPa) υ12=υ13 υ23
Graphite/epoxy 132 10.8 5.65 3.38 0.24 0.59
In addition, the thickness of each physical ply is assumed to be 0.5 mm (i.e., hk =   0.5 mm). HESL (i) represents that i number of (j = i) term is taken in (6). Clearly, as the number i is increased, the accuracy of the results is also increased. In the numerical examples that follow the interlaminar stresses are determined by integrating the local equilibrium equations of elasticity. Also, the width-to-thickness ratio (i.e., 2b/h) is assumed to be, unless otherwise mentioned, equal to 10. Furthermore, the stress components are normalized as
(21)
where σ0 = (1/bh )(F0 + M0/h  + T0/h ).

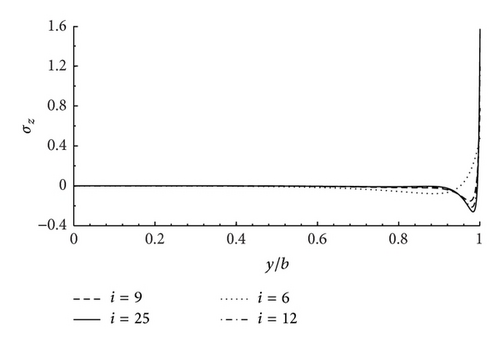
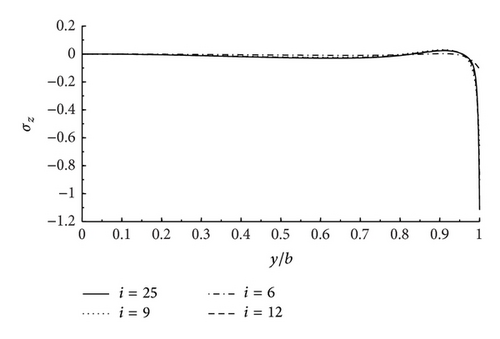
To study the convergence of the stresses near free edges, two symmetric laminates and subjected to the bending moment, the axial force, and the torque are considered. On account of the nature of the cross-ply laminates, both σxy and σxz are zero here as expected. Figures 2 and 3 demonstrate the convergence of the solution for σz versus y at the z = h/4 for the and laminates. It is seen that, for both and , σz is seen to rise or fall suddenly near the free edge, while being zero in the inner region of the laminate also the peak stress steadily increases as the number of terms (i) taken is increased. This is often attributed to a possible singularity at the 0°/90° interfaces.

Details are in the caption following the image
Figure 2
Open in figure viewerPowerPoint
Convergence of interlaminar normal stress along the 0°/90° interfaces of [90∘/0∘/0∘/90∘] laminate.
Details are in the caption following the image
Figure 3
Open in figure viewerPowerPoint
Convergence of interlaminar normal stress along the 0°/90° interfaces of [0∘/90∘/90∘/0∘] laminate.

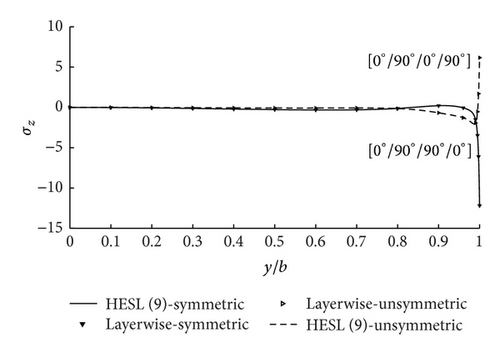
Numerical results are obtained from equilibrium equations. The present results are directly compared with those obtained from LWT. Figure 4 shows the σz distribution at the 0°/90° interfaces of [0°/90°/90°/0°] and [0°/90°/0°/90°] laminates under the bending moment and the axial force. An excellent agreement is found between the present solutions and those of LWT.

Details are in the caption following the image
Figure 4
Open in figure viewerPowerPoint
Distribution of interlaminar normal stress along the interfaces of [90∘/0∘/0∘/90∘] and [0∘/90∘/90∘/0∘] laminates.

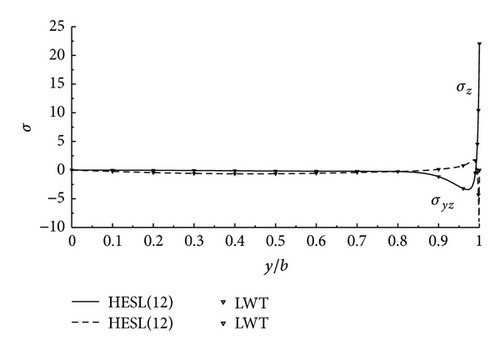
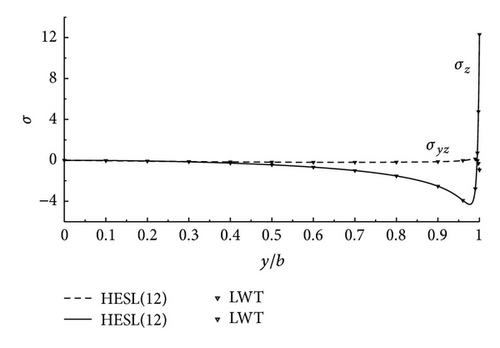
Figures 5 and 6 show the σz and σyz distribution at the 0°/90° interfaces of [0°/90°/90°/90°/90°/0°] and [0°/0°/0°/90°] laminates under the bending moment and the torque. Good accordance is seen between the results of the two theories. It is noted that the accuracy of HESL theory can be improved by taking more terms. Also the layerwise theory needs to take many terms to approach accurately the results of the present theory and these terms cause that LWT is more complex and computationally more time consuming than the HESL theory, so, it is better that HESL theory is used to compute the local phenomena such as free-edge-effect problems and the distribution of interlaminar stresses more precisely and less computationally than the layerwise theory in laminate composites.

Details are in the caption following the image
Figure 5
Open in figure viewerPowerPoint
Distribution of interlaminar stress along the 0∘/90∘ interface of [0∘/90∘/90∘/90∘/90∘/0∘] laminate.
Details are in the caption following the image
Figure 6
Open in figure viewerPowerPoint
Distribution of interlaminar stress along the 0∘/90∘ interface of [0∘/0∘/0∘/90∘] laminate.

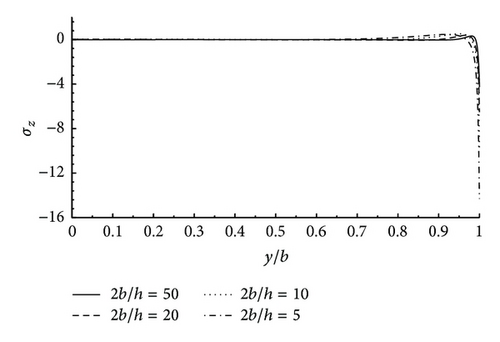
The effect of the laminate width-to-thickness ratio on the interlaminar stresses for the [90°/0°/90°/0°/90°/0°] laminate under the bending moment is investigated in Figure 7. By decreasing the width-to-thickness ratio, the boundary-layer region is expanded towards the internal region of the laminate with its width being almost equal to the thickness of the laminate. It is seen that the magnitude of the interlaminar stress at the free edge does not change while the width-to-thickness ratio of the laminate changes. On the other hand, this is evident that the highly localized nature of interlaminar stresses occurs near and exactly at the free edges of the laminate.

Details are in the caption following the image
Figure 7
Open in figure viewerPowerPoint
Distribution of interlaminar normal stress along the first 90∘/0∘ of [90∘/0∘/90∘/0∘/90∘/0∘] laminate for various width-to-thickness ratios.

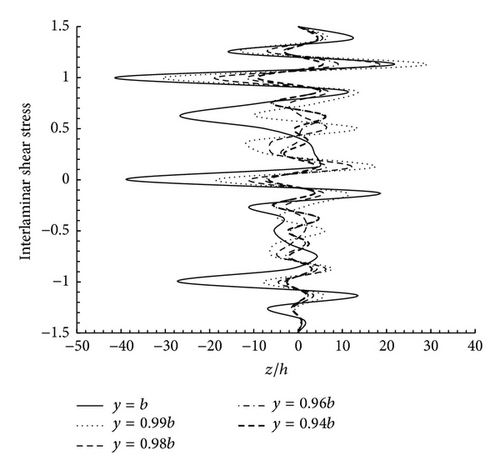
The variation of interlaminar shear stress σyz through the thickness and near the free edge of the [90°/0°/90°/0°] laminate under the bending moment and the torque is revealed in Figure 8. It is observed that the maximum negative and the maximum positive values of σyz occur within the bottom 90° layer and the top 0° layer at the 90°/0° interfaces of the laminate, respectively. The variations of interlaminar normal stress σz through the thickness of the unsymmetrical cross-ply laminate [90°/0°/90°/0°] under the bending moment and the axial force are portrayed in Figure 9. The maximum negative and the maximum positive values of σz occur within the bottom 90° layer and the top 0° layer both near the 90°/0° interfaces at the free edge (i.e., y = b), respectively. From Figure 9, it is seen that σz decreases away from the free edge as the inner region of the laminate is approached.

Details are in the caption following the image
Figure 8
Open in figure viewerPowerPoint
Distribution of interlaminar shear stress through thickness of [90∘/0∘/90∘/0] laminate.
Details are in the caption following the image
Figure 9
Open in figure viewerPowerPoint
Distribution of interlaminar normal stress through thickness of [90∘/0∘/90∘/0] laminate.

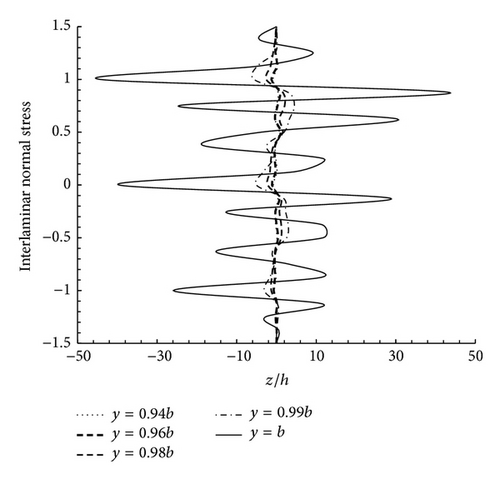
The distributions of the interlaminar stresses σz and σyz along the upper and lower interfaces of the unsymmetrical cross-ply [90°/90°/0°/90°] laminate subjected to the bending moment, the axial force, and the torque are demonstrated in Figure 10. It is observed that the interlaminar stresses demonstrate high stress gradient near the free edge. Both stresses are seen to grow suddenly near the free edge, while being zero in the interior region of the laminate. It is also observed that the interlaminar shear stress σyz rises toward the free edge and decreases (or increases) rather abruptly to zero at the free edge.

Details are in the caption following the image
Figure 10
Open in figure viewerPowerPoint
Distribution of interlaminar stress along the width in [90∘/90∘/0∘/90∘] laminate.

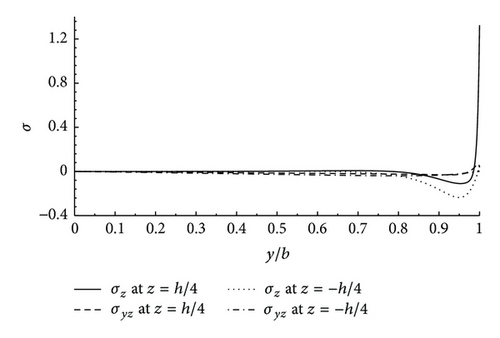
4.2. Preliminary Design Guidelines

A comprehensive structural analysis program for designing composite laminates is very extensive and complex. This generally involves several analysis phases such as laminate stress and strength analysis. Hence, there is still a need to provide some preliminary knowledge of the lay-up sequence of composite laminates. Usually, structural properties of composite laminates such as stiffness, strength, and dimensional stability are affected by the laminate stacking sequences. Because each property has different relations with a particular stacking sequence, the choice of stacking sequence suited for a particular application may require a compromise. The obtained preliminary design guidelines consist of the following.
  • (1)

    The laminates stacking sequence (LSS) should be symmetric about the midplane to avoid extension-bending coupling. If this is not possible due to other requirements, locate the asymmetry or imbalance as near to the laminate midplane as possible. Avoid symmetric LSS that create high interlaminar tension stresses (s) at free edges.

  • (2)

    Avoid grouping of 90° plies and separate 90° plies by a 0° ply to minimize interlaminar shear and normal stress. Minimize groupings of plies with the same orientations to create a more homogeneous laminate and to minimize interlaminar stress. If plies must be grouped, avoid grouping more than four plies of the same orientation. Minimizing grouping helps to increase strength and minimize interlaminar shear and normal stresses and therefore minimize the tendency to delaminate.

  • (3)

    Shield primary load carrying plies by positioning them inside of laminate to increase tensile strength and buckling resistance.

  • (4)

    An LSS should have at least both distinct ply angles (e.g., 0°, 90°) with a minimum of 10% of the plies oriented at each angle. Ply angles should be selected such that fibers are oriented with principal load axes.

  • (5)

    Locating 90° ply toward the exterior surfaces improves the buckling allowable in many cases.

5. Conclusions

In this research, analytical solutions were established within HESL theory for the edge-effect problem of general cross-ply composite laminates with finite dimensions under the bending moment, the axial force, and/or the torque. The edges of the laminates at y = ±b were assumed to have traction-free boundary conditions. The accuracy and effectiveness of HESL theory in describing the localized three-dimensional effects were demonstrated by comparing the results of HESL theory with those calculated from the layerwise theory. Good agreement was observed between the results of HESL and LWT theories. Furthermore, the analysis using HESL was found to be more cost effective and accurate, so HESL was employed to assess the local phenomena instead of LWT theory. Here, several numerical results were shown for the different loading problems. The design guidelines were developed to provide cross-ply laminate stacking sequences with minimized the free edges effects.

Conflict of Interests

The authors declare that there is no conflict of interests regarding the publication of this paper.

Appendices

A.

According to the principle of minimum total potential energy [22] at the equilibrium configuration of a body the variation of the total potential energy Π of the body must vanish as
(A.1)
where δU is the variation of total strain energy of the body; that is,
(A.2)
and V is negative of the work done on the body by the specified external forces. Here, V = −2M0aB6 − 2T0aB1 − 2F0aB2 and therefore, δV = −2M0aδB6 − 2T0aδB1 − 2F0aδB2. Also, the variations of strains in (A.2) are found as
(A.3)
Upon substituting (A.3) and δV = −2M0aδB6 − 2T0aδB1 − 2F0aδB2 into (A.1), carrying out the necessary integrations, and employing the fundamental lemma of calculus of variations the equilibrium equations and the associated boundary conditions of a laminate under bending are obtained to be as in (7a), (7b), (7c), and (7d), (8a), (8b), and (8c), and (12), respectively. To solve the linear equations in (13a), (13b), (13c), and (13d), first we obtained v′ and w′ from (13a) and (13b); then substituting v′ and w′ into (13c) and (13d) and integrating (13c) and (13d) yield
(A.4)
where
(A.5)
where [SP]  (P = 1,2, …, 6) and the vectors {SQ}  (Q = 7,8, 9) are n × m matrices containing SP(i, j) and m × 1 column matrices containing SQ(j), respectively. We introduced (A.4) in a matrix form as follows:
(A.6)
where
(A.7)
with
(A.8)
The general solution of (A.6) can be readily shown by
(A.9)
where [sinh⁡(λy)] is a 2n × 2 m diagonal matrix. Also in (A.9), [ψ] and represent the modal matrix and eigenvalues of (−[M]−1[K]), respectively. It is clear that [M]  and  [K] are (2n)×(2m) matrices containing SP(i, j)  (P = 1,2, …, 6) and [L] is 2m × 3 matrix containing SQ(i, j)  (Q = 7,8, 9). Also {H} is an unknown vector containing i + j constants of integration. Next, upon imposing the remaining boundary conditions (i.e., Aiy = Ajyz = 0 at either y = b or −b) in (12), the unknown vector {H} is determined in terms of vector{B}.

B.

The coefficients Akj, Bkj, and Dkj appearing in (19) are given as
(B.1)
The linear global interpolation function is defined as
(B.2)
where are the local Lagrangian linear interpolation functions within the kth layer which are defined as
(B.3)
with hk being the thickness of the kth layer.

C.

C.1. Analytical Solutions

The investigation is performed when analytically a rectangular composite laminate is subjected to the bending moment, the axial force, and the torque at its two opposite ends (x = −a and x = a) (see Figure 1). The linear Lagrangian interpolation functions through the thickness are used as in [26]. It is assumed that the laminates have invariably the traction-free boundary conditions at y = b and y = −b. The boundary conditions at these edges are considered as
(C.1)
Here the edges of the laminate are subjected to the bending moment M0, the axial force F0, and the torque T0 at x = ±a:
(C.2)
To find analytical solutions for (C.2), it is assumed that
(C.3)
Upon substitution of these expressions into (20), two sets of equations are obtained. The first set contains Uj(x), Vj(x), and Wj(x) which are expressed by
(C.4)
The second set of equations contains uj(x, y), vj(x, y), and wj(x, y) which are given by
(C.5)
It should be emphasized that a repeated index in (C.4) and (C.5) is a summation index from 1 to N + 1. When the boundary conditions (C.4) are considered, substituting (C.3) into (C.2) yields
(C.6a)
(C.6b)
(C.6c)
where
(C.7)
(C.8)
Equations (C.4) subjected to the boundary conditions (C.6a), (C.6b), and (C.6c) can be solved analytically. It is to be noted that there exist repeated zero roots (or eigenvalues) in the characteristic equation of the set of equations in (C.4). To improve the solution scheme of these equations, some small artificial terms are added to these equations so that the characteristic roots become all distinct. So, (C.4) are rewritten as
(C.9)
where, for convenience, αkj is assumed to be
(C.10)
where α is a prescribed number such that αkj’s in (C.10) are comparatively small compared to the numerical values of stiffnesses (pq = 33, 44, 55). The system of equations appearing in (C.9) is 3(N + 1) coupled second-order ordinary differential equations with constant coefficients which may be introduced in a matrix form as
(C.11)
where
(C.12a)
(C.12b)
The coefficient matrices [M] and [K] appearing in (C.11) are defined as
(C.12c)
(C.12d)
The general solution of (C.11) can be written as
(C.13)
where [sinh⁡(λx)], [ψ], and are a 3(N + 1) × 3(N + 1) diagonal matrix, the modal matrix, and eigenvalues of (−[M]−1[K]), respectively. In addition, {H} is an unknown vector containing 3(N + 1) integration constants. It should be noted that by satisfying the boundary condition in (C.6a), (C.6b), and (C.6c) the integration constants in {H} are found; then the problem is solved entirely.
It remains to solve (C.5) subject to the boundary conditions in (C.1) and (C.8). To this end, it is emphasized that the boundary conditions in (C.8) will identically be satisfied if the following expressions for the displacement components in (C.5) are assumed:
(C.14)
(C.15)
where α1m = mπ/a, α2m = mπ/2a with m are the Fourier integer. Upon substitution of (C.14) into (C.5), the following ordinary differential equations are obtained:
(C.16a)
(C.16b)
(C.17)
Considering (C.14), the boundary conditions in (C.1) at y = b and y = −b are given as
(C.18)
By introducing Fourier sine and cosine expansions for the underlined terms in (C.18), the following boundary conditions at y = b and y = −b can readily be obtained as
(C.19)
(C.20a)
(C.20b)
where
(C.21a)
where the coefficients Ik, Kk, and Jk appearing in (C.21a) are given as
(C.21b)
(C.21c)
In order to obtain the solution of (C.16a) and (C.16b), it is assumed that the boundary conditions at y = −b and y = b appearing in (C.20a) and (C.20b) are identical. To be able to impose the boundary conditions only at one edge, say, at y = b and, a significant advantage of this is to save some computational time, the system of equations appearing in (C.16a) are 3(N + 1) coupled second-order ordinary differential equations with constant coefficients which are introduced in a matrix form as
(C.22)
where
(C.23a)
(C.23b)
The coefficient matrices [S] and [G] appearing in (C.22) for solving (C.16a) are given as follows:
(C.23c)
The coefficient matrices [S] and [G] appearing in (C.22) for solving (C.16b) are given as
(C.23d)
The coefficient matrices [S] and [G] appearing in (C.22) for solving (C.17) are given as
(C.23e)
The general solution of (C.22) can be written as
(C.24)
where [sinh⁡(λy)], [ξ], and are a 3(N + 1) × 3(N + 1) diagonal matrix, the modal matrix, and eigenvalues of (−[S]−1[G]), respectively. Moreover, {B} is an unknown vector containing 3(N + 1) integration constants. By satisfying the boundary condition in (C.20a) only at one edge, say, at y = b, the integration constants in {B} are obtained; then the problem is solved completely.

The solution procedure for (C.16b) with the boundary conditions in (C.20b) and (C.17) and with the boundary conditions in (C.19) is similar to the one discussed in (C.16b), and therefore, for the sake of brevity, it will not be taken up here. The boundary conditions in (C.15) will identically be satisfied.

    The full text of this article hosted at iucr.org is unavailable due to technical difficulties.