This paper deals with the couple-group consensus problem for multiagent systems via output feedback control. Both continuous- and discrete-time cases are considered. The consensus problems are converted into the stability problem of the error systems by the system transformation. We obtain two necessary and sufficient conditions of couple-group consensus in different forms for each case. Two different algorithms are used to design the control gains for continuous- and discrete-time case, respectively. Finally, simulation examples are given to show the effectiveness of the proposed results.

1. Introduction

During the past decade, consensus problem of multiagent system has attracted a lot of attentions in control area [1–11]. It is mainly due to its wide applications in practice, such as sensor networks, unmanned aerial vehicles, and robotics. In [2], the authors studied the consensus seeking problem of multiagent systems with dynamically changing interaction topologies, where both discrete and continuous consensus algorithms were considered. In [9], the authors studied the containment problem of linear multiagent systems, where a pinning control strategy was designed for a part of agents such that all the agents can achieve a consensus with the leader asymptotically. A second-order consensus problem for multiagent systems with nonlinear dynamics and directed topologies was studied in [10]. More works about consensus problem were surveyed in [11].

Sometimes the interaction topology does not have a spanning tree, while it contains two or more subgraphs which include a spanning tree, respectively. In this case, some researchers studied the group consensus problem [12–15]. In [12], the authors studied the group consensus problem of multiagent systems with switching topologies. The group consensus was proved to be equivalent to the asymptotical stability of a class of switched linear systems by a double-tree-form transformation. In [13], two different kinds of consensus protocols were given to deal with the group consensus problem for double-integrator dynamic multiagent systems. In [15], the sampled-data control method was employed to deal with the group consensus problem for multiagent systems, where the interaction topology is undirected.

Sometimes the system states are not known completely, while the output of the systems is measurable. The output will be used to design the controller for this case, that is, output feedback controller. Recently, the output feedback control problems have been reported in a lot of literature [16–19]. In [16], the output feedback robust stabilization problem for a class of jump linear system was studied. In [17], the authors studied the finite-time stabilization of continuous-time linear systems via dynamic output feedback. In [18], the Lyapunov-Metzler inequalities were used to study the dynamic output feedback control problem of switched linear systems. Very recently, the method based on output feedback control has been used to analyze the networked systems [20–23]. In [20], the consensusability of a class of linear multiagent systems was studied, where the agent updates its information by using the neighbor’s output. In [21], the output regulation theory was used to study the output consensus problems for heterogeneous uncertain linear multiagent systems. In [22], by using appropriate coordinate transformation, a new consensus algorithm via dynamic output feedback control for multiagent systems was studied. While in [23], the joint effects of agent dynamic and network topology on the consensusability of linear discrete-time multiagent systems via relative output feedback were studied.

Motivated by the aforementioned works, we will investigate the couple-group consensus problems for multiagent systems via output feedback control. The systems considered include both continuous-time case and discrete-time case. We convert the couple-group consensus problems of multiagent systems into the stability problems of the error systems by a system transformation. Based on linear system theory, some necessary and sufficient conditions for couple-group consensus are obtained. For continuous-time case, the algorithm based on homotopy method is given to compute the allowable control gain. For discrete-time case, the algorithm based on cone complementary linearization method is given to compute the allowable control gain.

Notation. Let ℝ and ℕ represent, respectively, the real number set and the nonnegative integer set. Denote the spectral radius of the matrix M by ρ(M). Suppose that A, B ∈ ℝ^p×p. Let A⪰B (resp., A≻B) denote that A − B is symmetric positive semidefinite (resp., symmetric positive definite). I_n denotes the n × n identity matrix. Re(·) and Im⁡(·) represent, respectively, the real part and imaginary part of a number. Let 0 denote zero matrix with appropriate dimensions.

2. Preliminaries and Problem Formulation

Graph Theory. Let 𝒢 = (𝒱, ℰ, 𝒜) be a directed graph of order n, where 𝒱 = {v₁, …, v_n} and ℰ represent the node set and the edge set, respectively. 𝒜 = [a_ij] ∈ ℝ^n×n is the adjacency matrix associated with 𝒢, where a_ij > 0 if (v_i, v_j) ∈ ℰ, otherwise, a_ij = 0. An edge (v_i, v_j) ∈ ℰ if agent j can obtain the information from agent i. We say agent i is a neighbor of agent j. Let N_i = {v_j ∈ 𝒱 : (v_i, v_j) ∈ ℰ} denote the neighbor set of agent i. The (nonsymmetrical) Laplacian matrix ℒ associated with 𝒜 and hence 𝒢 is defined as ℒ = [l_ij] ∈ ℝ^n×n, where and l_ij = −a_ij, for all i ≠ j. A directed path is a sequence of edges in a directed graph in the form of , where . A directed tree is a directed graph, where every node has exactly one parent except for one node, called the root, which has no parent, and the root has a directed path to every other node. A directed spanning tree of 𝒢 is a directed tree that contains all nodes of 𝒢. A directed graph has or contains a directed spanning tree if there exists a directed spanning tree as a subset of the directed graph; that is, there exists at least one node having a directed path to all of the other nodes.

Suppose that the multiagent systems considered consist of n + m agents. In this paper, we will consider both continuous-time case and discrete-time case. We assume that the first n agents achieve a consistent state while the last m agents achieve another consistent state. Let 𝒢 = (𝒱, ℰ, 𝒜) denote the topology of multiagent system considered. Denote ℐ₁ = {1,2, …, n}, ℐ₂ = {n + 1, n + 2, …, n + m}. Let 𝒱₁ = {v₁, v₂, …, v_n} and 𝒱₂ = {v_n+1, v_n+2, …, v_n+m} represent the first n agents and the last m agents, respectively. Then, 𝒱 = 𝒱₁ ∪ 𝒱₂, 𝒱₁∩𝒱₂ = Φ. In addition, let N_1i = {v_j ∈ 𝒱₁ : (v_i, v_j) ∈ ℰ} and N_2i = {v_j ∈ 𝒱₂ : (v_i, v_j) ∈ ℰ}.

For continuous-time case, the ith agent’s dynamics are as follows:

(1)

where x_i(t) ∈ ℝ is the state, u_i(t) ∈ ℝ is the control input, and y_i(t) ∈ ℝ is the output. A, B, C ∈ ℝ are the system coefficients.

For discrete-time case, the ith agent’s dynamics are as follows:

(2)

where x_i[k] ∈ ℝ is the state, u_i[k] ∈ ℝ is the control input, and y_i[k] ∈ ℝ is the output. A, B, C ∈ ℝ are the system coefficients.

Sometimes the agent’s state is difficult to obtain, while the output is measurable. Our main purpose in this paper is to design consensus algorithm based on the output such that the multiagent systems can achieve couple-group consensus. We consider the following consensus algorithms for continuous-time case and discrete-time case, respectively.

Continuous-Time Case. Consider

(3)

where a_ij ≥ 0 for all i, j ∈ ℐ₁, a_ij ≥ 0 for all i, j ∈ ℐ₂, and a_ij ∈ ℝ for all (v_i, v_j) ∈ ℰ_o = {(i, j) : i ∈ ℐ₁, j ∈ ℐ₂}∪{(i, j) : j ∈ ℐ₁, i ∈ ℐ₂}. α is the control gain to be designed.

Discrete-Time Case. Consider

(4)

where a_ij ≥ 0 for all i, j ∈ ℐ₁, a_ij ≥ 0 for all i, j ∈ ℐ₂, and a_ij ∈ ℝ for all (v_i, v_j) ∈ ℰ_o = {(i, j) : i ∈ ℐ₁, j ∈ ℐ₂}∪{(i, j) : j ∈ ℐ₁, i ∈ ℐ₂}. γ is the control gain to be designed. In addition, we suppose the algorithms in (3) and (4) satisfy similar assumption to that of [24].

Assumption 1. for all i ∈ ℐ₁; for all i ∈ ℐ₂.

Assumption 2. The subgraphs 𝒢₁ and 𝒢₂ have a directed spanning tree, respectively.

Denote X(t)≜[x₁(t), …, x_n+m(t)] ^T. Using (3) in (1) yields

(5)

where ℒ₁ and ℒ₂ are the Laplacian matrices corresponding to subgraphs 𝒢₁ and 𝒢₂, respectively, and

(6)

Denote X[k]≜[x₁[k], …, x_n+m[k]] ^T. Using (4) in (2) yields

(7)

where ℒ₁, ℒ₂, Ω₁, and Ω₂ are the same as that of continuous-time case.

Remark 3. The group consensus problem of continuous time multiagent systems was studied in [12, 13, 15]. In [14], the authors studied the group consensus problem for discrete-time multiagent systems. However, the couple-group consensus problem for the multiagent systems with stochastic switching topologies has not been researched. In addition, our method in this paper is based on the output feedback control, which is different from the existing results.

Our main purpose is to give the conditions for couple-group consensus. We next convert the consensus problem of multiagent system into the stability problem of the error systems. Before giving the main results, the following definitions and lemma are needed.

Definition 4 (see [24].)The multiagent system in (5) is said to achieve couple-group consensus if the states of agents satisfy (i) lim⁡_t→∞∥x_i(t) − x_j(t)∥ = 0, for all i, j ∈ ℐ₁ and (ii) lim⁡_t→∞∥x_i(t) − x_j(t)∥ = 0, for all i, j ∈ ℐ₂.

Definition 5 (see [24].)The multiagent system in (7) is said to achieve couple-group consensus if the states of agents satisfy (i) lim⁡_k→∞∥x_i[k] − x_j[k]∥ = 0, for all i, j ∈ ℐ₁ and (ii) lim⁡_k→∞∥x_i[k] − x_j[k]∥ = 0, for all i, j ∈ ℐ₂.

Lemma 6 (see [25] Schur complements.)Consider a hermitian matrix Q such that . Then, Q≻0 if and only if

(8)

(9)

3. Main Results

In this section, we will give the main results of this paper.

3.1. Continuous-Time Case

Let

(10)

Then by some computations, we obtain the error systems as follows:

(11)

where

(12)

Here we have used Assumption 1 and the property of Laplacian matrix.

Now the couple-group consensus problem of (5) has been converted into the stability problem of error system (11). We next give our main results.

Theorem 7. The multiagent system (5) can achieve couple-group consensus asymptotically if and only if α satisfies A + αBCRe(μ_i) < 0, where μ_i (i = 1, …, n + m − 2) is the ith eigenvalue of .

Proof. According to the aforementioned discussion, we know that the multiagent systems (5) can achieve couple-group consensus asymptotically if and only if the error system (11) is asymptotically stable. It follows from linear system theory [26] that system (11) which is asymptotically stable is equivalent to all eigenvalues of F_c having negative real parts. Denote the ith eigenvalues of F_c and , respectively, by η_i and μ_i (i = 1, …, n + m − 2). Then, η_i = A + αBCμ_i. Re(η_i) < 0 is equivalent to A + αBCRe(μ_i) < 0. This completes the proof.

Remark 8. Theorem 7 provides a necessary and sufficient condition of couple-group consensus for multiagent system (5). According to linear system theory, we know that system (11) which is asymptotically stable is equivalent to that in which there exists a positive matrix P such that . Hence, we can get another condition of couple-group consensus for multiagent systems (5).

Theorem 9. The multiagent system (5) can achieve couple-group consensus asymptotically if and only if there exists a positive definite matrix P such that

(13)

holds.

Proof. The proof is straightforward; here is omitted.

Remark 10. Theorem 9 gives a necessary and sufficient condition for couple-group consensus in forms of matrix inequality. However, the matrix inequality in (13) is nonlinear with regard to variables α and P. Here we provide a numerical algorithm based on homotopy method to solve this problem. The similar method can be found in [22, 27, 28].

Algorithm 11. Consider the following

Step 1. Introduce a real number λ varying from 0 to 1, and construct a matrix function

(14)

with F₁(P) = 2AP, .

Step 2 (Set λ = 0). Compute the initial value of P₀ by solving the LMI H(α, P, 0)≺0.

Step 3. Increase λ by some homotopy path, such as λ = (k/M) (k = 1,2, …, M). M is a large positive integer, for example, M = 1000. Compute α⁰ by solving LMI H(α, P₀, 1/M)≺0.

Step 4. Increase λ by the same homotopy path as Step 3. Compute P₁ by solving LMI H(α⁰, P, 2/M)≺0.

Step 5. Repeat Steps 3 and 4 until λ reaches Step 1.

3.2. Discrete-Time Case

Similar to continuous-time case, we can get the similar results for discrete-time case.

Let

(15)

Then by some computations, we obtain the error systems as follows:

(16)

where

(17)

Here we have used Assumption 1 and the property of Laplacian matrix.

Now the couple-group consensus problem of (7) has been converted into the stability problem of error system (16). We next give our main results.

Theorem 12. The multiagent system (7) can achieve couple-group consensus asymptotically if and only if γ and (A, B, C) satisfy

(18)

where μ_i (i = 1, …, n + m − 2) is the ith eigenvalue of

Proof. According to the aforementioned discussion, we know that the multiagent systems (7) can achieve couple-group consensus asymptotically if and only if the error system (16) is asymptotically stable. It follows from linear system theory [26] that system (16) which is asymptotically stable is equivalent to all eigenvalues of F_c being within the unit circle. Denote the ith eigenvalues of by μ_i (i = 1, …, n + m − 2). Then ρ(F_d) < 1 is equivalent to (A + αBCRe(μ_i)) ² + (αBCIm⁡(μ_i)) ² < 1. That is,

(19)

By some computations, we know that if the conditions in (18) hold, then the inequality (19) is solvable. This completes the proof.

Remark 13. Theorem 12 provides a necessary and sufficient condition of couple-group consensus for multiagent system (7). According to linear system theory, we know that system (16) which is asymptotically stable is equivalent to that in which there exists a positive matrix P such that . Hence, we can get another condition of couple-group consensus for multiagent systems (7).

Theorem 14. The multiagent system (7) can achieve couple-group consensus asymptotically if and only if there exist positive definite matrices P, Q and scalar γ such that the following LMI

(20)

holds with the constraint P⁻¹ = Q. Here F_d is defined in (16).

Proof. According to the discussion in Remark 13, and by using Schur complement lemma (Lemma 6) and letting Q≜P⁻¹, the proof can be obtained. This completes the proof.

Remark 15. Theorem 14 provides a necessary and sufficient condition of couple-group consensus for multiagent systems (7). We can get γ by solving LMI in (20) with constrain P⁻¹ = Q. The cone complementarity linearization (CCL) method can be used to solve this problem [19, 29]. We next summarize the algorithm as follows.

Algorithm 16. Consider the following

Step 1. Find a feasible point of LMI (20) γ⁰, P⁰, Q⁰, set k = 0. If there are none, exit.

Step 2. Find γ^k+1, P^k+1, Q^k+1 by solving the convex minimization problem

(21)

s.t.

(22)

Step 3. If t_k = 2(n + m − 2), end this algorithm, and the feasible γ is given by γ = γ^k+1. Otherwise, set k = k + 1 and go to Step 2.

4. Simulation Examples

In this section, two examples will be given to show the usefulness of the theoretical results. For simplicity, we let a_ij = 1 if (i, j) ∈ ℰ. On the other hand, we suppose that a_ij takes values in a set {−1,0, 1} for v_i, v_j belonging to different node sets, respectively.

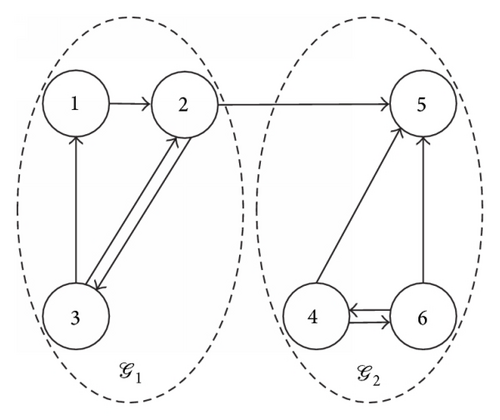
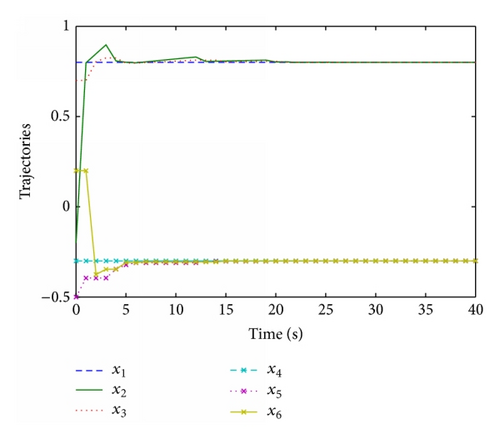
Example 1. This example is for continuous-time multiagent systems. The interaction topology is as shown in Figure 1, which includes six nodes. It can be seen that the graph contains two subgraphs 𝒢₁ and 𝒢₂. (v₁, v₂, v₃) ∈ 𝒢₁, (v₄, v₅, v₆) ∈ 𝒢₂. Each of them has a directed spanning tree. Let A = 0.3, B = 0.8, and C = −0.9. By solving the optimization problem in Algorithm 11, we obtain α = 0.6304 and

(23)

The state trajectories of the agents are as shown in Figure 2. It can be seen that the agents belonging to 𝒢₁ and 𝒢₂ achieve two different consistent states, respectively.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Topology 𝒢.

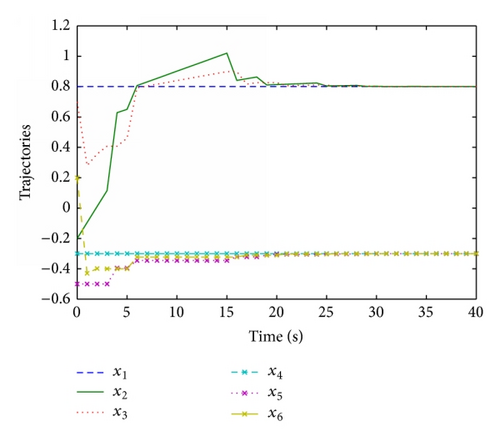
Example 2. This example is for discrete-time multiagent systems. For simplicity, we suppose that the interaction topology is the same as that of continuous-time case, that is, 𝒢. Let A = 0.4, B = 0.7, and C = −0.8. By solving the optimization problem in Algorithm 16, we obtain γ = −0.2531 and

(24)

Figure 3 shows the consensus results.

5. Conclusion

In this paper, we have studied the couple-group consensus problems for both continuous-time and discrete-time multiagent systems via output feedback control. By a system transformation, the consensus problems of multiagent systems have been converted into the stability problems of the error systems. Some necessary and sufficient conditions of couple-group consensus for multiagent systems have been obtained. Two algorithms have been given to compute the allowable control gains. The effectiveness of the proposed results has been shown by the simulation examples.

Conflict of Interests

The authors declare that there is no conflict of interests regarding the publication of this paper.

Acknowledgment

The work was supported by the National Natural Science Foundation of China under Grants nos. 61203056, 61104007, 61203024, 61273123, and 61374061.

References

1 Ren W. and Beard R. W., Distributed Consensus in Multi-Vehicle Cooperative Control, 2008, Springer, Berlin, Germany.
10.1007/978-1-84800-015-5
Google Scholar
2 Ren W. and Beard R. W., Consensus seeking in multiagent systems under dynamically changing interaction topologies, IEEE Transactions on Automatic Control. (2005) 50, no. 5, 655–661, https://doi.org/10.1109/TAC.2005.846556, MR2141568.
10.1109/TAC.2005.846556
Web of Science® Google Scholar
3 Ren W., Multi-vehicle consensus with a time-varying reference state, Systems & Control Letters. (2007) 56, no. 7-8, 474–483, https://doi.org/10.1016/j.sysconle.2007.01.002, MR2331998, ZBL1157.90459.
10.1016/j.sysconle.2007.01.002
Web of Science® Google Scholar
4 Mei J., Ren W., and Ma G., Distributed coordinated tracking with a dynamic leader for multiple Euler-Lagrange systems, IEEE Transactions on Automatic Control. (2011) 56, no. 6, 1415–1421, https://doi.org/10.1109/TAC.2011.2109437, MR2839235.
10.1109/TAC.2011.2109437
Web of Science® Google Scholar
5 Qin J., Gao H., and Zheng W. X., On average consensus in directed networks of agents with switching topology and time delay, International Journal of Systems Science. (2011) 42, no. 12, 1947–1956, https://doi.org/10.1080/00207721003802271, MR2845435, ZBL1260.93003.
10.1080/00207721003802271
Web of Science® Google Scholar
6 Zhao H., Ren W., Yuan D., and Chen J., Distributed discrete-time coordinated tracking with Markovian switching topologies, Systems & Control Letters. (2012) 61, no. 7, 766–772, https://doi.org/10.1016/j.sysconle.2012.04.003, MR2930323, ZBL1250.93018.
10.1016/j.sysconle.2012.04.003
Web of Science® Google Scholar
7 Yuan D., Xu S., Zhao H., and Rong L., Distributed dual averaging method for multi-agent optimization with quantized communication, Systems & Control Letters. (2012) 61, no. 11, 1053–1061, https://doi.org/10.1016/j.sysconle.2012.06.004, MR2982985, ZBL1252.93008.
10.1016/j.sysconle.2012.06.004
Web of Science® Google Scholar
8 Wen G., Duan Z., Li Z., and Chen G., Consensus and its L₂-gain performance of multi-agent systems with intermittent information transmissions, International Journal of Control. (2012) 85, no. 4, 384–396, https://doi.org/10.1080/00207179.2011.654264, MR2892864.
10.1080/00207179.2011.654264
Web of Science® Google Scholar
9 Liu H., Xie G., and Wang L., Containment of linear multi-agent systems under general interaction topologies, Systems & Control Letters. (2012) 61, no. 4, 528–534, https://doi.org/10.1016/j.sysconle.2012.01.012, MR2910328, ZBL1250.93010.
10.1016/j.sysconle.2012.01.012
Web of Science® Google Scholar
10 Yu W., Chen G., Cao M., and Kurths J., Second-Order consensus for multiagent systems with directed topologies and nonlinear dynamics, IEEE Transactions on Systems, Man, and Cybernetics, Part B: Cybernetics. (2010) 40, no. 3, 881–891, 2-s2.0-77952581942, https://doi.org/10.1109/TSMCB.2009.2031624.
10.1109/TSMCB.2009.2031624
PubMed Web of Science® Google Scholar
11 Cao Y. C., Yu W. W., Ren W., and Chen G. R., An overview of recent progress in the study of distributed multi-agent coordination, IEEE Transactions on Industrial Informatics. (2013) 9, no. 1, 427–438, https://doi.org/10.1109/TII.2012.2219061.
10.1109/TII.2012.2219061
Web of Science® Google Scholar
12 Yu J. and Wang L., Group consensus in multi-agent systems with switching topologies, Proceedings of the 48th IEEE Conference on Decision and Control held jointly with 2009 28th Chinese Control Conference (CDC/CCC ′09), December 2009, 2652–2657, 2-s2.0-77950827284, https://doi.org/10.1109/CDC.2009.5400096.
10.1109/CDC.2009.5400096
Google Scholar
13 Feng Y. Z., Xu S. Y., and Zhang B. Y., Group consensus control for double-integrator dynamic multiagent systems with fixed communication topology, International Journal of Robust and Nonlinear Control. (2014) 24, no. 3, 532–547, https://doi.org/10.1002/rnc.2904.
10.1002/rnc.2904
Web of Science® Google Scholar
14 Feng Y., Lu J., Xu S., and Zou Y., Couple-group consensus for multi-agent networks of agents with discrete-time second-order dynamics, Journal of the Franklin Institute. (2013) 350, no. 10, 3277–3292, https://doi.org/10.1016/j.jfranklin.2013.07.004, MR3123418.
10.1016/j.jfranklin.2013.07.004
Web of Science® Google Scholar
15 Yu J., Yu M., Hu J., and Liu B., Group consensus in multi-agent systems with sampled data, Proceedings of the 30th Chinese Control Conference, 2013, Xi’an, China, 7168–7172.
Google Scholar
16 Boukas E. K. and Liu Z. K., Output feedback robust stabilization of jump linear system with mode-dependent time-delays, Proceedings of the American Control Conference, June 2001, Arlington, Va, USA, 4683–4688, 2-s2.0-0034847705.
Google Scholar
17 Amato F., Ariola M., and Cosentino C., Finite-time stabilization via dynamic output feedback, Automatica. (2006) 42, no. 2, 337–342, https://doi.org/10.1016/j.automatica.2005.09.007, MR2195173, ZBL1099.93042.
10.1016/j.automatica.2005.09.007
Web of Science® Google Scholar
18 Geromel J. C., Colaneri P., and Bolzern P., Dynamic output feedback control of switched linear systems, IEEE Transactions on Automatic Control. (2008) 53, no. 3, 720–733, https://doi.org/10.1109/TAC.2008.919860, MR2401024.
10.1109/TAC.2008.919860
Web of Science® Google Scholar
19 Feng J.-e., Lam J., Li P., and Shu Z., Decay rate constrained stabilization of positive systems using static output feedback, International Journal of Robust and Nonlinear Control. (2011) 21, no. 1, 44–54, https://doi.org/10.1002/rnc.1575, MR2789978, ZBL1207.93080.
10.1002/rnc.1575
Web of Science® Google Scholar
20 Ma C.-Q. and Zhang J.-F., Necessary and sufficient conditions for consensusability of linear multi-agent systems, IEEE Transactions on Automatic Control. (2010) 55, no. 5, 1263–1268, https://doi.org/10.1109/TAC.2010.2042764, MR2642097.
10.1109/TAC.2010.2042764
Web of Science® Google Scholar
21 Kim H., Shim H., and Seo J. H., Output consensus of heterogeneous uncertain linear multi-agent systems, IEEE Transactions on Automatic Control. (2011) 56, no. 1, 200–206, https://doi.org/10.1109/TAC.2010.2088710, MR2777219.
10.1109/TAC.2010.2088710
CAS Web of Science® Google Scholar
22 Zhai G., Okuno S., Imae J., and Kobayashi T., A new consensus algorithm for multi-agent systems via dynamic output feedback control, Proceedings of the IEEE International Symposlum on Intelligent Control, Part of 2009 IEEE Multi-conference on Systems and Control, July 2009, Saint Petersburg, Russia, 890–895, 2-s2.0-74049097949, https://doi.org/10.1109/CCA.2009.5281163.
10.1109/CCA.2009.5281163
Google Scholar
23 You K. and Xie L., Coordination of discrete-time multi-agent systems via relative output feedback, International Journal of Robust and Nonlinear Control. (2011) 21, no. 13, 1587–1605, https://doi.org/10.1002/rnc.1659, MR2856097, ZBL1227.93013.
10.1002/rnc.1659
Web of Science® Google Scholar
24 Yu J. and Wang L., Group consensus of multi-agent systems with undirected communication graphs, Proceedings of the 7th Asian Control Conference (ASCC ′09), August 2009, Hong Kong, 105–110, 2-s2.0-71449093998.
Google Scholar
25 Saberi A., Sannuti P., and Chen B. M., ℋ2-Optimal Control, 1995, Prentice-Hall.
Google Scholar
26 Boyd S., El Ghaoui L., Feron E., and Balakrishnan V., Linear Matrix Inequalities in System and Control Theory, 1994, 15, SIAM, Philadelphia, Pa, USA, SIAM Studies in Applied Mathematics, https://doi.org/10.1137/1.9781611970777, MR1284712.
10.1137/1.9781611970777
Google Scholar
27 Zhai G., Ikeda M., and Fujisaki Y., Decentralized H_∞ controller design: a matrix inequality approach using a homotopy method, Automatica. (2001) 37, no. 4, 565–572, https://doi.org/10.1016/S0005-1098(00)00190-4, MR1832530, ZBL0982.93035.
10.1016/S0005-1098(00)00190-4
Web of Science® Google Scholar
28 Richter S. L. and DeCarlo R. A., Continuation methods: theory and applications, Institute of Electrical and Electronic Engineers. Transactions on Systems, Man, and Cybernetics. (1983) 13, no. 4, 459–464, https://doi.org/10.1109/TAC.1983.1103294, MR713910.
10.1109/TAC.1983.1103294
Google Scholar
29 El Ghaoui L., Oustry F., and AitRami M., A cone complementarity linearization algorithm for static output-feedback and related problems, IEEE Transactions on Automatic Control. (1997) 42, no. 8, 1171–1176, https://doi.org/10.1109/9.618250, MR1469081, ZBL0887.93017.
10.1109/9.618250
Web of Science® Google Scholar

All articles

Output Feedback Control for Couple-Group Consensus of Multiagent Systems

Abstract

1. Introduction

2. Preliminaries and Problem Formulation

3. Main Results

3.1. Continuous-Time Case

3.2. Discrete-Time Case

4. Simulation Examples

5. Conclusion

Conflict of Interests

Acknowledgment

References

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Output Feedback Control for Couple-Group Consensus of Multiagent Systems

Abstract

1. Introduction

2. Preliminaries and Problem Formulation

3. Main Results

3.1. Continuous-Time Case

3.2. Discrete-Time Case

4. Simulation Examples

5. Conclusion

Conflict of Interests

Acknowledgment

References

Figures

References

Related

Information