As for uncertainties and decision-makers’ overconfidence psychological bias, overconfidence has been incorporated into real option decision-making model of metal mineral resources mining to estimate its effect on decision-making of the project and thus a behavioral real option decision-making model of metal mineral resources mining based on overconfidence has been established. Furthermore, numerical simulation and sensitivity analysis have been conducted to verify the practicality of the model. Results show that model in this paper has greatly changed trigger value and option value of mineral resources mining project compared with traditional real option model, thus greatly changing optimal decision results. Incorporating overconfidence into real option decision-making model of metal mineral resources development is a crucial extension of project evaluation theory.

1. Introduction

Metal mineral resources are essential base material and important strategic supplies in economic development. Metal mineral resources mining project bears large budget, long construction cycle, and high risks and it is influenced by external factors including metal mineral market supply and demand, technological progress and policies, and internal factors including decision-maker’s working capacity and psychological bias, which could take effect on evaluation of metal mineral resources mining project [1]. This makes it difficult to evaluate metal mineral resources mining project by traditional DCF method accurately. Recently, with considerable researches in this field, real option approach (ROA), which is firstly brought up by Myers and Turnbull [2] and Ross [3], has been generally accepted as an appropriate method to help make decisions of metal mineral resources mining under uncertain circumstances. Brennan and Schwartz [4] initiated ROA into copper mining project, Smith and Nau [5] and Smith and McCardle [6] analyzed hydrocarbon resource development project by using dynamic programming and option pricing. Lately, scholars tend to investigate relationship between investment decision making and uncertain factors, operation cost uncertainty [7], production uncertainty [8], full-cost uncertainty [9], and exchange rate uncertainty [10, 11], have become vital factors which have expanded ROA model.

In the literature, ROA is increasingly applied to study metal mineral resources mining by scholars, but there still exists a widespread problem. In real option theory, scholars generally presume investment decision-makers are completely rational; ROA model only considers external uncertainties and ignores internal uncertainties factors including overconfidence, risk preference, and herd effect existing in economic activities [12, 13]. On the premise of investors’ limited rationalities, real market scenes can hardly be simulated through experiment and results of investors’ transaction accounts are often not representative [14]. Therefore, incorporating heterogeneous beliefs into real option model is of great significance, amongst which overconfidence is a prior. In fact, a great number of behavioral finance literatures have demonstrated that overconfidence bias of decision-makers takes great effect on investment decisions. Cooper et al. [15] and Russo and Schoemaker [16] proved that both entrepreneurs and managers showed overconfidence; Odean [17] made a comparison between investment decisions made by rational and overconfident managers and it turned out that overconfident managers tended to accept earlier investment; Hao et al. [18] through empirical approach analyzed relationship between overconfident CEO and investment. Results showed that overconfident CEO was more likely to conduct inefficient allocation of overinvestment. In incorporating overconfidence to real option theory, Hu and Ye [19] concentrated on uncertainties caused by the managers and revised the “approximate twin securities” approach, thus improving traditional real option evaluation. Throughout the abovementioned literatures, researches which incorporated overconfidence bias into real option model are at premium. A few studies have focused on qualitative analysis and very few scholars conducted quantitative analysis on impacts of overconfidence exerted by real option evaluation.

Therefore, aiming at this relatively blank field, overconfidence is incorporated into a real option decision-making model of metal mineral resources mining project in this paper and “twin security” is applied to build a connection between real option and overconfidence psychological bias. Since the ubiquitous overconfidence in decision-makers can change their estimation of expected growth rate and volatility of project value, the changes will take effect on the option pricing through the abovementioned key factors. On these premises, this paper establishes a behavioral real option price model and lists the numerical result of the model. In the context of China’s metal mineral resources mining projects, overconfidence of decision-makers ought to be incorporated into real option model, which could help make metal mineral resources investment decisions more precisely.

This paper is organized as follows. Section 2 establishes the model; Section 3 provides numerical results and discussions; Section 4 presents the concluding comments and final discussion.

2. Establishment of Model

2.1. Basic Assumptions

Uncertainties such as irreversibility and capability to defer contribute to real option value. But since there exists no real option trading market, it is impossible to apply a standard financial option pricing model to price real option. Fortunately, theoretical study by Mason and Merton [20] indicates once a “twin security” which bears the same risk features as the project can be found in the stock market, method of a standard option pricing model can be applied to derive real option pricing model under the same assumptions as standard DCF method. Since the existence of a “twin security” requires a standardized market and the same risk and distribution features as the project to be evaluated, it is difficult to find a “twin security” for a project whose underlying asset is not tradable [21]. But as for metal mineral resources mining project, its underlying asset is tradable in standardized active stock market, for example, “LME copper futures market,” which makes the metal mineral products standardized and tradable; additionally, the price volatility of metal mineral future is consistent with the value of the mining project, which exhibits the same risk features. Furthermore, the price motion of metal mineral future is similar to the value of the mining project; that is, they follow geometric Brownian motion; thus, metal mineral futures can be applied as the “twin security” of the metal mineral mining project as evidenced by Hu and Ye [19] and Trigeorgis [22] and Zhu [23]. By using the combination of “twin security” and risk-free security, the yield features of relevant real option can be copied. Consequently, the real option model can be solved by the same way of option pricing initiated by Black-Scholes [24–26].

In addition, as a form of risky security, twin security will inevitably meet the basic features of the risky securities and traditional behavioral asset pricing theory based on overconfidence is generally built on the premise of risk stock market [27] and assumes price of risk security is a normal random variable. On the abovementioned analysis, we take metal mineral futures as the “twin security” of the metal mineral mining project, through which contact between twin security market volatility and cognitive volatility of overconfident investors can be established. Ultimately, information of twin security can be used to indicate the value and volatility of metal mineral resources mining projects under investors’ overconfidence conditions.

On these premises, it is reasonable to assume that (1) the project to be decided is at a perfect competition market and there exists a tradable “twin security” θ, which shows the same risk features with the project and follows normal distribution

, so the project value is affected by the equivalent uncertain factors of “twin security”; (2) the initial cost I of the project is fixed; (3) decision-makers of the project are overconfident; (4) price of the metal mineral product follows geometric Brownian motion:

()

where μ₁ stands for expected rate of growth, σ₁ stands for volatility, and dz₁ is a standard Wiener process. Since value of the project is mainly affected by price, the value of project is also follows:

()

Malmendier and Tate pointed out that entrepreneurs and business managers show overconfidence and investment decision-makers of metal mining projects are often middle-senior managers; these managers are often faced with a variety of complex issues and thus they are more likely to exhibit higher overconfidence bias than the ordinary group. Numerous studies [28, 29] documented overconfident investment decision-makers estimated expected growth rates and project value volatility with error. Therefore, they estimate α as α_o and σ as σ_o. So (2) turns to (3) under the condition of investment decision-makers’ overconfidence:

()

where V_o stands for the value of metal mineral mining project when taking overconfidence of investment decision-makers into consideration, α_o shows the cognitive expectation when investment decision-makers are overconfident, σ_o is the cognitive volatility when decision-makers are overconfident, and dz is a standard Wiener process. Copying the project value by “twin security” in the metal mineral futures market, “twin security” under investment makers’ overconfidence follows geometric Brownian motion as well:

()

Mathematical description of overconfidence in the model is particularly important so as to make real option decision-making model of mineral resources development based on overconfidence which is more persuasive in explaining reality of economic phenomena. Representative overconfidence measurement methods are as follows: Gervais and Goldstein defined overconfidence level d = A − a, in which d was overconfidence level, A was the cognitive capability of the overconfident, a meant the actual capability of the overconfident decision-maker, and A > a. Keiber figured out that, when analyzing relationship between variables in stock market, it can be inevitably affected by random variables; the distribution of the random variable ε was assumed to meet normal distribution

. The existence of overconfidence decreased the variance of the random variable ε to kσ² (0 < k < 1); k stood for overconfidence level because of their own experiences and ability. But the measurement method of overconfidence in DHS model is most generally accepted and widely used, where it was assumed that overconfident investment decision-makers were influenced by private signals in the stock market and overconfidence coefficient ϕ (0 < ϕ < 1) indicated that noise factor variance was underestimated. Based on the above theories, overconfidence can be incorporated into real option model of mineral resources mining.

2.2. Model Construction

When starting to make decisions on the metal mineral resources mining project, overconfident investment decision-makers will receive private signal S which is related to “twin security” in stock market and the signal is random which follows

()

where θ follows normal distribution (

), ε is a noise factor which follows normal distribution

) and it is a one-dimensional random variable, and θ and ε are independent of each other. According to features of one-dimensional random variables, variance of signal S is as follows:

()

could be understood as the market risk of “twin security” of metal mineral product which would not be affected by capability of decision-makers,

is a risk relevant with the effort of the decision-makers’ capability; namely, it is dominantly affected by the capability and overconfidence level of the decision-makers. According to Gervais and Odean [27] and Daniel et al. [29], overconfident decision-makers will overestimate the accuracy of the information and underestimate risk that is facing them, namely, underestimation of noise variance

. Assume that there exists a coefficient ϕ (0 < ϕ < 1) which turns the estimation of noise variance under investment decision-makers’ overconfidence into

()

The lower the ϕ is, the higher the overconfidence level is. In order to facilitate the following context, we also take ϕ = 1 into account and in this circumstance equation (7) turns into a situation when investment decision-makers are completely rational with no overconfidence bias. The “twin security” that is affected by private signals (θ∣S) also follows normal distribution; the expected value and cognitive volatility under investment decision-maker’s overconfidence condition are, respectively, [30]

()

It is easy to prove that , so the overconfident investment decision-makers underestimate the volatility of metal mineral resources mining project, thus generating great impact on decision-making.

As for overconfident decision-maker of metal mineral resources mining project, generally we can assume his utility function is [31]

()

where risk averse coefficient a > 0; in order to simplify the following analysis, we take a = 1; W is the wealth hold by the decision-maker. Under such conditions, when the overconfident decision-maker tends to make optimal decision in the “twin security” market of metal mineral resources mining project, the following requirements need to be met:

()

where Q_r0 stands for the quantity of “twin security” hold by overconfident decision-maker before decision making, Q_r1 is the quantity of “twin security” hold by overconfident decision-maker after decision making, Q_f0 is the quantity of the risk-free security hold by overconfident decision-maker before decision-making, and Q_f1 is the quantity of the risk-free security hold by overconfident decision-maker after decision-making. The first constraint condition means, as for overconfident decision-maker, the investment capitals before decision-making equals that after decision-making and the second constraint condition stands for the total wealth after decision-making.

Derive the solution of the abovementioned problem, we arrive at

()

Therefore, the optimal solution is

()

When the twin security market is at the equilibrium state, the supply equals demand at metal mineral futures market; that is,

()

Combine (8), (9), (13), and (14); the equilibrium price of the twin security θ when taking decision-maker’s overconfidence into account can be written as

()

where

stands for average holding quantity of twin security. Therefore, the cognitive expectation of the metal mineral’s twin security when taking decision-maker’s overconfidence into account turns to

()

It is easy to prove that overconfidence coefficient and the cognitive expectation of the metal mineral’s twin security show negative correlation, which means when overconfidence coefficient decreases, the cognitive expectation of the metal mineral’s twin security increases. In order to facilitate the following analysis, we take

. Put (9) and (16) into (3); the value of metal mineral resources mining project under decision-makers’ overconfidence condition can be described as follows:

()

2.3. Model Solution

According to Dixit and Pindyck [32], F(V) stands for investment option value and V stands for value of metal mineral resources development project. Assume that there is no time boundary in decision making of mining investment. When investment decision-makers are overconfident, the Bellman equation of investment option value in continuous time can be presented as

()

With boundary conditions,

()

where ϕ is overconfidence coefficient,

is volatility of “twin security”,

is volatility of noise factor which stands for investment cost of investing the project, r is discount rate, and δ is dividend, it could be interpreted as the convenience yield of metal mineral resources mining project or the opportunity cost to delay the project. According to option pricing method given by Dixit and Pindyck, investment option value and value of the project are, respectively, as follows:

()

A and V^* can be obtained with the boundary conditions and V^* stands for trigger value in optimal investment timing:

()

where C stands for operation cost of investment project. Substituting the parameters into differential equation, parameters β₁ and β₂ can be obtained:

()

According to boundary conditions and V(P), V^′(P) is continuous at P = C; we arrive at

()

Based on value matching and smooth paste conditions of Pindyck, we get to

()

And P^* is the solution of (24):

()

Using numerical method, we can get value of P^*. The abovementioned equations give the option value, project value, and boundary conditions in optimal investment; we can get trigger value to carry out the investment when investment decision-makers are overconfident.

3. Numerical Results and Discussions

3.1. Main Parameters

In order to apply the model to estimate the effect of overconfidence on trigger value V^* and option value, a domestic copper mining project has been considered with the value of technical and economic parameters as those presented in Table 1. The life span of the project is 20 years, initial investment cost is 9.3 billion yuan, the cost of production is 8967.54 yuan per ton, yearly production is 1,010,000 ton, and risk free rate is 3.48%.

Table 1. Main technical and economic parameters of the copper mining project.

Input parameters	Units	Value
Initial investment (I)	RMB billion yuan	9.3
Cost of production (C)	RMB yuan/ton	8967.54
Yearly production of copper ore (q)	Ton	1010000
Risk-free interest rate (r)	%	3.48
Twin security’s volatility (σ_θ)	%	22.46
Noise factor’s volatility (σ_ε)	%	31.4
Overconfidence coefficient (ϕ)	Dimensionless	0.5
Yearly convenience yield (δ)	%	1.48
Life span of the project (L)	Year	20
Initial price of copper	RMB yuan/ton	28950

On the premise of the analysis, the copper futures in LME futures market are adopted as the “twin security” of the copper mining project and as for the projects that can find “twin securities” in stock market, the volatility of “twin securities” is often used to substitute that of real assets projects [22, 23]. Therefore, the volatility of copper futures in LME is applied to present the project twin security’s volatility σ_θ of copper mining project. σ_θ is extracted from LME copper price on daily basis from October 2003 to October 2013 [33]; from the data we get standard deviation of copper price during these ten years 22.46%; risk-free rate is one-year treasury rate in 2013 and convenience yield is 1.48%. The estimation of noise factor’s volatility σ_ε is more subjective, since there is no publicly available information regarding it. Consequently, in this case, assume that σ_ε = 31.4% is just a first approximation.

3.2. Numerical Results and Discussions

Since only when the project value exceeds the trigger value can the investment of the project be carried out, trigger value is the prior evaluation criteria. Additionally, option value presents the value to delay the project; it has also been taken into consideration as key evaluation criteria. The following data and analysis show how overconfidence coefficient affects optimal decision timing in the copper mining project.

3.2.1. Effects of Overconfidence Coefficient on Decision-Making

Impacts of overconfidence on project trigger value and option value are mainly focused in this paper; part of the numerical data is shown from Tables 2, 3, and 4. In order to decrease the possible error caused by subjective estimation, simulation results under different σ_ε value are given as follows.

Table 2. Simulation result under different overconfidence coefficient (σ_ε = 0.214).

Overconfidence coefficient	Trigger value	Option value
0.05	3.995 × 10¹¹	3.902 × 10¹¹
0.10	4.144 × 10¹¹	4.051 × 10¹¹
0.15	4.258 × 10¹¹	4.165 × 10¹¹
0.20	4.353 × 10¹¹	4.260 × 10¹¹
0.25	4.434 × 10¹¹	4.341 × 10¹¹
0.30	4.505 × 10¹¹	4.412 × 10¹¹
0.35	4.568 × 10¹¹	4.475 × 10¹¹
0.40	4.625 × 10¹¹	4.532 × 10¹¹
0.45	4.677 × 10¹¹	4.584 × 10¹¹
0.50	4.724 × 10¹¹	4.631 × 10¹¹
0.55	4.767 × 10¹¹	4.674 × 10¹¹
0.60	4.807 × 10¹¹	4.714 × 10¹¹
0.65	4.843 × 10¹¹	4.750 × 10¹¹
0.70	4.878 × 10¹¹	4.785 × 10¹¹
0.75	4.909 × 10¹¹	4.816 × 10¹¹
0.80	4.939 × 10¹¹	4.846 × 10¹¹
0.85	4.967 × 10¹¹	4.874 × 10¹¹
0.90	4.993 × 10¹¹	4.900 × 10¹¹
0.95	5.017 × 10¹¹	4.924 × 10¹¹
1.00	5.040 × 10¹¹	4.947 × 10¹¹

Table 3. Simulation result under different overconfidence coefficient (σ_ε = 0.314).

Overconfidence coefficient	Trigger value	Option value
0.05	4.163 × 10¹¹	4.070 × 10¹¹
0.10	4.378 × 10¹¹	4.286 × 10¹¹
0.15	4.534 × 10¹¹	4.442 × 10¹¹
0.20	4.657 × 10¹¹	4.564 × 10¹¹
0.25	4.757 × 10¹¹	4.664 × 10¹¹
0.30	4.841 × 10¹¹	4.748 × 10¹¹
0.35	4.911 × 10¹¹	4.818 × 10¹¹
0.40	4.973 × 10¹¹	4.880 × 10¹¹
0.45	5.026 × 10¹¹	4.933 × 10¹¹
0.50	5.073 × 10¹¹	4.980 × 10¹¹
0.55	5.115 × 10¹¹	5.022 × 10¹¹
0.60	5.152 × 10¹¹	5.059 × 10¹¹
0.65	5.186 × 10¹¹	5.093 × 10¹¹
0.70	5.216 × 10¹¹	5.123 × 10¹¹
0.75	5.244 × 10¹¹	5.151 × 10¹¹
0.80	5.270 × 10¹¹	5.176 × 10¹¹
0.85	5.292 × 10¹¹	5.199 × 10¹¹
0.90	5.313 × 10¹¹	5.220 × 10¹¹
0.95	5.333 × 10¹¹	5.240 × 10¹¹
1.00	5.351 × 10¹¹	5.258 × 10¹¹

Table 4. Simulation result under different overconfidence coefficient (σ_ε = 0.414).

Overconfidence coefficient	Trigger value	Option value
0.05	4.330 × 10¹¹	4.237 × 10¹¹
0.10	4.597 × 10¹¹	4.504 × 10¹¹
0.15	4.776 × 10¹¹	4.683 × 10¹¹
0.20	4.908 × 10¹¹	4.815 × 10¹¹
0.25	5.010 × 10¹¹	4.917 × 10¹¹
0.30	5.092 × 10¹¹	4.999 × 10¹¹
0.35	5.158 × 10¹¹	5.065 × 10¹¹
0.40	5.213 × 10¹¹	5.120 × 10¹¹
0.45	5.260 × 10¹¹	5.167 × 10¹¹
0.50	5.300 × 10¹¹	5.207 × 10¹¹
0.55	5.335 × 10¹¹	5.242 × 10¹¹
0.60	5.366 × 10¹¹	5.273 × 10¹¹
0.65	5.393 × 10¹¹	5.300 × 10¹¹
0.70	5.417 × 10¹¹	5.324 × 10¹¹
0.75	5.439 × 10¹¹	5.346 × 10¹¹
0.80	5.458 × 10¹¹	5.365 × 10¹¹
0.85	5.476 × 10¹¹	5.383 × 10¹¹
0.90	5.492 × 10¹¹	5.399 × 10¹¹
0.95	5.506 × 10¹¹	5.413 × 10¹¹
1.00	5.520 × 10¹¹	5.427 × 10¹¹

Note: when overconfidence coefficient is 1, it means that investment decision-maker bears no overconfidence. Since it has no negative effect on the model, the data has been kept for further illustration.

Since the metal mineral resources mining project is faced with great uncertainty, the trigger condition of the project is that the value of metal mineral mining project exceeds the trigger value. Therefore, according to Table 2 to Table 4, we can figure out the following.

(1) Owing to the existence of overconfidence, investment decision-makers are too optimistic about market price and thus they will carry out the project when project value is beneath proper trigger value. The model also echoes from another perspective that overconfident investment decision-makers tend to implement project earlier which has been proved by Odean [17] and Sarkar [34], thus increasing the possibility of failure.

(2) As overconfidence coefficient grows, namely, overconfidence level decreases, trigger value of the project is increasingly getting close to 5.351 × 10¹¹ (when σ_ε = 0.314); in other words, the conclusion can be interpreted as with increase of overconfidence level; overconfident decision-makers will underestimate the trigger value to a greater extent; possibility to carry out the project earlier is growing as well as the risk of fault investment decision.

(3) The estimation of option value by overconfident decision-maker is lower than that of rational decision-maker, which means that overconfident decision-maker bears the belief that the present metal mineral price is high so the option value to defer the project is relatively low and there is no need in waiting for new opportunities.

(4) The overconfidence coefficient shows positive correlation with project option value. As the overconfidence coefficient increases, the investment decision-maker will underestimate the option value to a greater extent. Overconfident decision-maker thinks that the project’s delay option value is not high; they tend to give up waiting for new market opportunity and carry out the metal mineral resource mining project earlier.

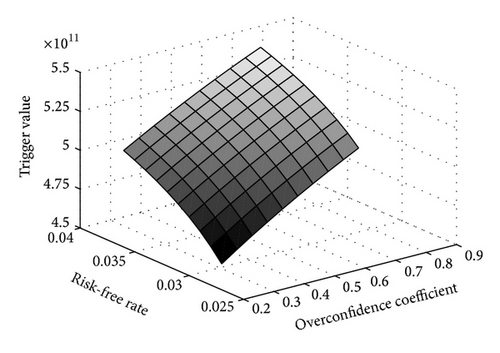
Figures 1 and 2 show, respectively, impact of overconfidence coefficient on trigger value and option value under different noise factor volatilities. From Figure 1, it can be concluded that, when overconfidence coefficient increases or decreases 1% from 0.1, trigger value will change −0.845% and 0.794%, respectively; when overconfidence coefficient increases or decreases 1% from 0.5, trigger value will change −0.176% and 0.172%, respectively; when overconfidence coefficient increases or decreases 1% from 0.9, trigger value will change −0.077% and 0.076%, respectively. Therefore, in the interval where the overconfidence level is high, the overconfident investment decision-makers will underestimate the trigger value to a greater extent and thus overconfidence generates greater impacts on decision-making. When overconfidence coefficient gets close to 1, estimation error is approximately 0.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Impact of overconfidence coefficient on critical investment value.

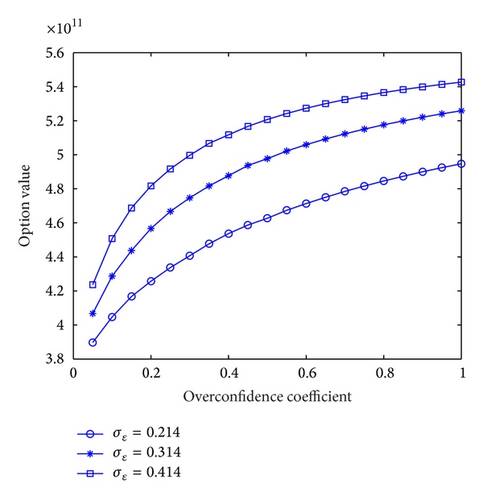
Figure 2 indicates that overconfidence coefficient and the option value show positive correlation. When overconfidence coefficient increases or decreases 1% from 0.1, the option value will change −0.86293% and 0.81135%; when overconfidence coefficient increases or decreases 1% from 0.5, the option value will change −0.17967% and 0.17546%; when overconfidence coefficient increases or decreases 1% from 0.9, the option value will change −0.07906% and 0.07782%. This on the one hand shows that, due to investment decision-maker’s overconfidence, option value of project is underestimated by the decision-maker; on the other hand, it indicates that in the interval where the overconfidence level is high, impact of overconfidence to option value is greater and vice versa. When overconfidence coefficient gets close to 1, the option value of the model gets close to the value when the investment decision-maker is not overconfident.

3.2.2. A Comparison Analysis of Numerical Results between the Proposed and DCF Approach

In order to clarify the different effects of the proposed and classic approaches on decision-making and exhibit the superior performance of the proposed model, comparison studies of the real option decision-making model which incorporates overconfidence and classic DCF method, Black-Scholes formula based model, Monte Carlo based model has been presented.

According to market information, the expected growth rate of copper product is 0.005. Applying (1) and Ito′s Lemma, the copper price P_t in the year t follows lognormal distribution, based on the features of which the expected value of P_t can be described as in the following expression:

()

Therefore, the net present value (NPV) of the copper mining project is presented by

()

Table 5 shows evaluation results between the DCF and the real option method. The net present value of copper mining project by traditional DCF method is 7.867 × 10¹¹; therefore the project is feasible and should be immediately carried out. Conversely, the evaluation result by RO method indicates that immediate investment is not an optimal decision, because it means the investment decision-maker gives up the delay option value 4.980 × 10¹¹. Even if price uncertainty and overconfidence brings up the project value, a delay investment is an optimal decision.

Table 5. The comparison of the evaluation results between the DCF and the proposed model.

Method	Feature	Trigger value	Option value	Investment decision
Traditional DCF	Ignoring uncertainty and investment flexibility	9.300 × 10⁹	—	Make investment immediately
Proposed model (ϕ = 0.5)	Incorporating uncertainty and investment flexibility into the model	5.073 × 10¹¹	4.980 × 10¹¹	Delay investment

Therefore, DCF method cannot reflect the uncertainty and investment flexibility, which means an ignorance of the option value of the copper mining project, while, as for the proposed model which takes the price uncertainty and overconfidence into the real option model, the delay option value reflects such added value brought by these uncertainties.

3.2.3. A Comparison Analysis of Numerical Results between Traditional Black-Scholes Formula Based and the Proposed Model

The simulation results of traditional BS formula based and the proposed model of this copper mining project are shown in Table 6.

Table 6. The comparison of the evaluation results between traditional BS based formula and the proposed model.

Method	Feature	Trigger value	Option value	Investment decision
Traditional BS model	Ignoring investment maker’s overconfidence bias	5.838 × 10¹¹	5.745 × 10¹¹	Wait and delay investment
Proposed model (ϕ = 0.5)	Incorporating overconfidence into the model	5.073 × 10¹¹	4.980 × 10¹¹	Early investment*

Note: *denotes that the evaluation result is compared with the investment decision made through traditional BS approach.

Table 6 exhibits the evaluation results of traditional BS based formula and the proposed model. As can be seen in Table 6, option value of the model which incorporates overconfidence is beneath that of the traditional real option model with no overconfidence bias (5.745 × 10¹¹); therefore the proposed model proves that overconfident decision-maker usually underestimates the delay option value and loses the opportunity to wait for better market information, thus resulting in early investment compared with the evaluation results of traditional BS approach. On the other hand, the trigger value of the project in new model is below that of traditional BS model since overconfidence bias contributes to the optimistic estimation of the market price of metal mineral so overconfident decision-maker often exercises the project when the value does not exceed proper trigger value. Overconfident decision-maker bears higher risks in making fault investment decisions.

3.2.4. A Comparison Analysis of Numerical Results between the Proposed and Monte Carlo Based Model

The copper mining project can be understood as an American option; the following part gives the option pricing results based on Monte Carlo simulation [34]. According to the previous parameters and results, the initial price of the real option is 7.87 × 10¹¹ yuan and the exercise price of the real option is 9.3 × 10⁹; all the other necessary parameters can be obtained in Table 1. We take 1000 simulation sample paths and divide each discrete time interval into 20 steps which added to 400 steps for each path. Part of the simulation result is shown in Figure 3.

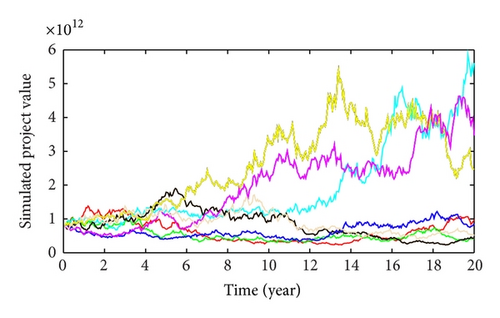
Comparison of the evaluation results between Monte Carlo based model and the proposed model is presented in Table 7. It shows that overconfident decision-maker underestimates the option value of the copper mining investment project, which means an underestimation of the value to wait for new market information. This evaluation result is consistent with the results in previous part. In addition, the comparison shows that our proposed model can determine the optimal timing of copper mining investment project, while the traditional Monte Carlo simulation cannot solve it, which also reflects the superiority of the proposed model.

Table 7. The comparison of the evaluation results between Monte Carlo based model and the proposed model.

Method	Feature	Trigger value	Option value	Investment decision
Monte Carlo based model	Optimal investment timing cannot be obtained	—	5.562 × 10¹¹	Wait and delay investment
Proposed model (ϕ = 0.5)	Optimal investment timing can be obtained	5.073 × 10¹¹	4.980 × 10¹¹	Early investment*

Note: *denotes that the evaluation results are compared with the investment decision made through traditional Monte Carlo based approach.

3.3. Sensitivity Analysis

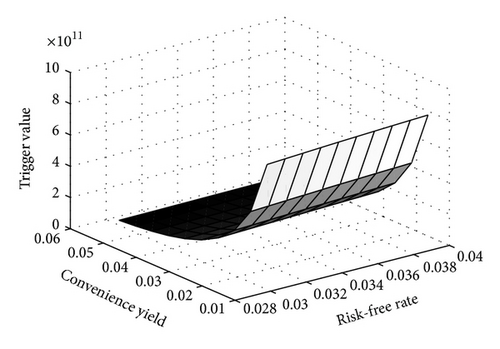
In order to ensure the stability of model, sensitivity of main parameters in this paper is conducted; results are shown in Figures 4 and 5. From the two figures, trigger value is the most sensitive to convenience yield, which is consistent with traditional conclusion and this ensures the stability of the model. In this paper, when convenience yield decreases or increases 1% from 3.48%, it will contribute to 83.2% and −38.73% change in the trigger value; it should be noted that, as convenience yield goes up, its impact on trigger value goes down. The newly incorporated parameters in this paper, that is, overconfidence coefficient, noise factor volatility, and twin security volatility, also take effect on trigger value as analyzed in the previous chapter. When noise volatility goes up or down 1% from 31.4%, the trigger value changes −0.176% and 0.172%, respectively, while the sensitivity of trigger value to twin security volatility falls in the interval between overconfidence coefficient and noise factor volatility.

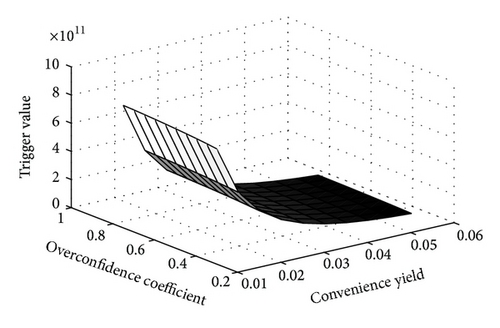
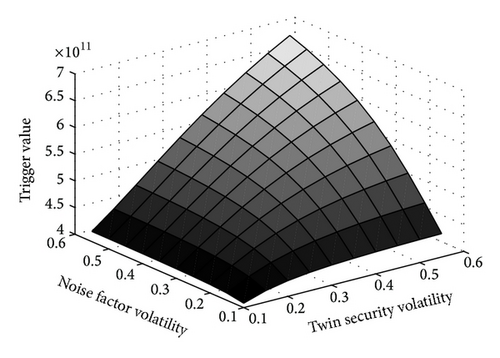
Figure 6 exhibits that, when risk free rate increases, trigger value increases and vice versa. When risk-free rate decreases or increases 1% from 2.48%, the trigger value changes −19.056% and 13.7214%, respectively; when risk-free rate decreases or increases 1% from 4.48% the trigger value changes −7.87% and 5.7385%, respectively. Comparatively, the sensitivity of trigger value to overconfidence coefficient is lower than that to convenience yield. Figure 7 also shows that the sensitivity of trigger value to risk-free rate is lower than that to convenience yield.

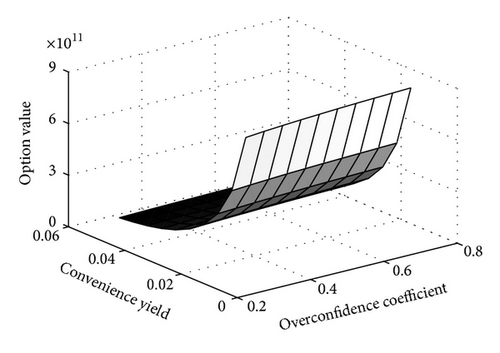
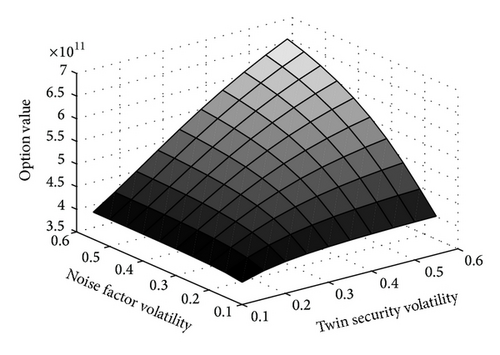
In order to estimate the effect of main parameters to option value of the model, the sensitivity analysis of option value to overconfidence coefficient, convenience yield, noise factor volatility, and twin security volatility has been given. Results show that option value presents the greatest sensitivity to convenience yield among the input parameters. Figure 8 shows relatively higher convenience yield can decrease the option value to defer. When overconfidence coefficient takes 0.5, convenience yield decreases or increases 1% from 2% and option value changes 164.22% or −50.61%; while when convince yield is 1.48%, when overconfidence coefficient decreases or increases 1% from 0.1, the option value just changes −0.86293% and 0.81135%, respectively. Figure 9 shows that both higher noise factor volatility and twin security volatility add the delay option value in the proposed model, which is consistent with traditional research findings, while the sensitivity levels to the two factors are quite close.

4. Conclusion

This paper considers the shortage of traditional real option approach when making investment decisions of metal mineral resources mining project and establishes a behavioral real option decision-making model which is incorporated with overconfidence. Finally, analytical solution of the model has been given. To further illustrate the theoretical value and practical significance of the model, we use the data of a domestic copper mining project to conduct example and sensitivity analysis; results show the following. (1) Overconfidence is an important factor in decision making of metal mineral resources mining projects and, according to the results of the model, overconfident investment decision-makers will underestimate trigger value of the implementation of the project and the greater the degree of overconfidence is, the greater the degree of underestimation of the trigger value will be. Therefore when decision-makers show overconfidence bias in reality, optimal investment value of project should be higher than the trigger value assessed by the overconfident investment decision-makers so as to effectively avoid the risk brought by overconfidence. (2) Presence of overconfidence decreases uncertainty of metal mineral resources development investment since the overconfident decision-maker generally underestimates the volatility of the project value; consequently, the delay option value in metal mineral resources development investment increases as overconfidence coefficient increases. These findings echo previous study of Sarkar [34]. (3) Convenience yield of metal mineral resources is an important factor for evaluation of metal mineral resources project. Through sensitivity analysis of the model, it can be figured out that convenience yield generates the greatest impact on the valuation of metal mineral resource projects; relatively higher convenience yield will reduce the trigger value of mineral resources investment projects. While the convenience yield reflects the abundance of metal mineral resources, so it is important for overconfident decision-makers to consider the abundance of mineral resources when making a metal mineral resources development decision. Because high resource abundance of the project can bring higher investment income and offset the risk brought by decision-makers’ overconfidence to some extent.

Existence of overconfidence contributes to investment in advance and overinvestment into metal mineral resources market. These findings also provide a theoretical basis for phenomenon of excess investment in metal mining industry of iron and steel. But model in this paper shows some deficiencies; the paper fails to take cost uncertainty of metal mineral resources development and measurement of overconfidence into account. In future studies, it is not only meaningful to build a more realistic and accurate metal mineral resources investment decision-making model with the consideration of cost and other uncertainties, but also of theoretical value and realistic significance by incorporating overconfidence into real option models.

Conflict of Interests

The authors declare that there is no conflict of interests regarding the publication of this paper.

Acknowledgments

This work was partially supported by National Natural Science Foundation of China (NSFC) under Grant no. 71073177, Ministry of Education of International Financial Crisis Emergency Response Project under Grant no. 2009JYJR035, the National Natural Science Foundation of China (Grant no. 71171203), Major Project of National Social Science Foundation (Grant nos. 13 and ZD024 and nos. 13 and ZD169), the Ph.D. Programs Foundation of Ministry of Education of China (Grant no. 20130162110076), the Research Project in Humanities and Social Sciences of Chinese Ministry of Education (Grant nos. 13YJAZH149 and 09YJC90261), the Emergency Project of Chinese Ministry of Education (Grant no. 2009JYJR035), the Postgraduate Autonomous Exploration Innovation Fund of Central South University (Grant no. 2013zzts141), the China Postdoctoral Science Foundation (Grant no. 20110491264), the Special Project of Postdoctoral Research Funds of Hunan Province (Grant no. S2011R1040), and the Project of Soft Science of Hunan Province (Grant no. 2009ZK3193).

References

1 Zhong M. R., Chen J. Y., Zhu X. H., and Huang J. B., Strategic equilibrium price analysis and numerical simulation of preponderant high-tech metal mineral resources, Transactions of Nonferrous Metals Society of China. (2013) 23, no. 10, 3153–3160, https://doi.org/10.1016/S1003-6326(13)62846-0.
10.1016/S1003-6326(13)62846-0
Web of Science® Google Scholar
2 Myers S. C. and Turnbull S. M., Capital budgeting and the capital asset pricing model: good news and bad news, The Journal of Finance. (1977) no. 32, 321–333.
10.1111/j.1540-6261.1977.tb03272.x
Web of Science® Google Scholar
3 Ross S. A., A simple approach to the valuation of risky income streams, Journal of Business. (1978) 51, 453–475.
10.1086/296008
Web of Science® Google Scholar
4 Brennan M. J. and Schwartz E. S., Evaluation natural resource investments, Journal of Business. (1985) 58, no. 2, 135–149.
10.1086/296288
Web of Science® Google Scholar
5 Smith J. E. and Nau R. F., Valuing risky projects: option pricing theory and decision analysis, Management Science. (1995) 41, no. 5, 795–816.
10.1287/mnsc.41.5.795
Web of Science® Google Scholar
6 Smith J. E. and McCardle K. F., Valuing oil properties: integrating option pricing and decision analysis approaches, Operations Research. (1998) 46, no. 2, 198–217, https://doi.org/10.1287/opre.46.2.198, 2-s2.0-0032021949.
10.1287/opre.46.2.198
Web of Science® Google Scholar
7 Lima C., Gabriel A., and Suslick B. S., Estimating the volatility of mining projects considering price and operating cost uncertainties, Resources Policy. (2006) 31, no. 2, 86–94, https://doi.org/10.1016/j.resourpol.2006.07.002.
10.1016/j.resourpol.2006.07.002
Web of Science® Google Scholar
8 Evatt G. W., Soltan M. O., and Johnson P. V., Mineral reserves under price uncertainty, Resources Policy. (2012) 37, no. 3, 340–345, https://doi.org/10.1016/j.resourpol.2012.03.004, 2-s2.0-84865580978.
10.1016/j.resourpol.2012.03.004
Web of Science® Google Scholar
9 Dehghani H. and Ataee-pour M., Determination of the effect of operating cost uncertainty on mining project evaluation, Resources Policy. (2012) 37, no. 1, 109–117, https://doi.org/10.1016/j.resourpol.2011.11.001, 2-s2.0-84860577437.
10.1016/j.resourpol.2011.11.001
Web of Science® Google Scholar
10 Zhu L. and Fan Y., A real options-based CCS investment evaluation model: case study of China′s power generation sector, Applied Energy. (2011) 88, no. 12, 4320–4333, https://doi.org/10.1016/j.apenergy.2011.04.005, 2-s2.0-80052261171.
10.1016/j.apenergy.2011.04.005
Web of Science® Google Scholar
11 Fan Y., Mo J., and Zhu L., Evaluating coal bed methane investment in China based on a real options model, Resources Policy. (2013) 38, no. 1, 50–59, https://doi.org/10.1016/j.resourpol.2012.08.002, 2-s2.0-84873260723.
10.1016/j.resourpol.2012.08.002
Web of Science® Google Scholar
12 Wen F., He Z., and Chen X., Investors’ risk preference characteristics and conditional skewness, Mathematical Problems in Engineering. (2014) 2014, 14, 814965, https://doi.org/10.1155/2014/814965.
10.1155/2014/814965
Web of Science® Google Scholar
13 Wen F., He Z., Gong X., and Liu A., Investors′ risk preference characteristics based on different rEFerence POInt, Discrete Dynamics in Nature and Society. (2014) 2014, 9, 158386, https://doi.org/10.1155/2014/158386, MR3198314.
10.1155/2014/158386
Web of Science® Google Scholar
14 Wen F., Gong X., Chao Y., and Chen X., The effects of prior outcomes on risky choice: evidence from the stock market, Mathematical Problems in Engineering. (2014) 2014, 8, 272518, https://doi.org/10.1155/2014/272518, MR3193662.
10.1155/2014/272518
Web of Science® Google Scholar
15 Cooper A. C., Woo C. Y., and Dunkelberg W. C., Entrepreneurs′ perceived chances for success, Journal of Business Venturing. (1988) 3, no. 2, 97–108, https://doi.org/10.1016/0883-9026(88)90020-1, 2-s2.0-38249027897.
10.1016/0883-9026(88)90020-1
Web of Science® Google Scholar
16 Russo J. E. and Schoemaker P. J., Managing overconfidence, Sloan Management Review. (1992) 33, 7–17.
PubMed Web of Science® Google Scholar
17 Odean T., Volume, volatility, price, and profit when all traders are above average, Journal of Finance. (1998) 53, no. 6, 1887–1934, https://doi.org/10.1111/0022-1082.00078, 2-s2.0-0346907827.
10.1111/0022-1082.00078
Web of Science® Google Scholar
18 Hao Y., Liu X., and Lin C., Executives of listed companies and investment decisions overconfidence empirical research, China Management Science. (2005) 10, no. 13, 142–147.
Google Scholar
19 Hu W. and Ye G., Influence on the valuation of options of risky project put by Project manager, Operations Research and Management. (2003) 2, no. 12, 105–109.
Google Scholar
20 Mason S. P. and Merton R. C., The Role of Contingent Claims Analysis in Corporate Finance, 1984, Division of Research, Graduate School of Business Administration, Harvard University.
Google Scholar
21 M. J. Brennan and L. Trigeorgis, Project Flexibility, Agency, and Competition: New Developments in the Theory and Application of Real Options, 2000, Oxford University Press.
Google Scholar
22 Trigeorgis L., Real Options: Managerial Flexibility and Strategy in Resource Allocation, 1996, MIT Press.
Web of Science® Google Scholar
23 Zhu D., Project investment decision-making methods research based on real options, 2009, no. no. 6, Northeastern University.
Google Scholar
24 Huang J. B. and Zhong M. R., Real options theory and its applications, Economic Management. (2002) 12, 30–33.
Google Scholar
25 Li S. and Liu Y., Mining investment decision model based on real options delayed, Systems Engineering. (2008) 3, 124–126.
Google Scholar
26 He M. and Liu J., Outsourcing opportunity decision-making model based on real options, Systems Engineering. (2011) 5, 38–42.
Google Scholar
27 Gervais S. and Odean T., Learning to be overconfident, The Review of Financial Studies. (2001) 14, no. 1, 1–27, https://doi.org/10.1093/rfs/14.1.1, 2-s2.0-0035583183.
10.1093/rfs/14.1.1
Web of Science® Google Scholar
28 Malmendier U. and Tate G., CEO overconfidence and corporate investment, Journal of Finance. (2005) 60, no. 6, 2661–2700, https://doi.org/10.1111/j.1540-6261.2005.00813.x, 2-s2.0-27544450102.
10.1111/j.1540-6261.2005.00813.x
Web of Science® Google Scholar
29 Daniel K. D., Hirshleifer D., and Subrahmanyam A., Investor psychology and security market under-and overreactions, The Journal of Finance. (1998) 53, no. 6, 1839–1885, https://doi.org/10.1111/0022-1082.00077, 2-s2.0-8744258405.
10.1111/0022-1082.00077
Web of Science® Google Scholar
30 Gui H., Cai M., and Wu W., A commentary overconfidence research model approach, Financial Research. (2007) 2, 98–109.
Google Scholar
31 Chen Q., Gao G., and Chen H., Pricing model of Chinese stock market based on individual investors overconfidence, China Management Science. (2011) 4, no. 8, 38–46.
Google Scholar
32 Dixit A. and Pindyck R., Investment under Uncertainty, 1994, Princeton University Press, Princeton, NJ, USA.
10.1515/9781400830176
Google Scholar
33 Wen F. and Yang X., Skewness of return distribution and coefficient of risk premium, Journal of Systems Science and Complexity. (2009) 22, no. 3, 360–371, https://doi.org/10.1007/s11424-009-9170-x, MR2538868, 2-s2.0-71449108473.
10.1007/s11424-009-9170-x
Web of Science® Google Scholar
34 Sarkar S., On the investment-uncertainty relationship in a real options model, Journal of Economic Dynamics and Control. (2000) 24, no. 2, 219–225, https://doi.org/10.1016/S0165-1889(99)00005-6, ZBLl1036.91510, 2-s2.0-0000993176.
10.1016/S0165-1889(99)00005-6
Web of Science® Google Scholar

Citing Literature

All articles

Incorporating Overconfidence into Real Option Decision-Making Model of Metal Mineral Resources Mining Project

Abstract

1. Introduction