Journal of Quality and Reliability Engineering
Volume 2014, Issue 1 192072
Research Article
Open Access

Interval Estimation of Stress-Strength Reliability Based on Lower Record Values from Inverse Rayleigh Distribution

Bahman Tarvirdizade, 

Corresponding Author

Bahman Tarvirdizade

Department of Statistics, Islamic Azad University, Maku Branch, Maku, Iran iau.ac.ir

Search for more papers by this author
Hossein Kazemzadeh Garehchobogh, 

Hossein Kazemzadeh Garehchobogh

Department of Statistics, Islamic Azad University, Maku Branch, Maku, Iran iau.ac.ir

Search for more papers by this author
First published: 16 November 2014
https://doi.org/10.1155/2014/192072
Citations: 4
Academic Editor: Adiel Teixeira de Almeida

Abstract

We consider the estimation of stress-strength reliability based on lower record values when X and Y are independently but not identically inverse Rayleigh distributed random variables. The maximum likelihood, Bayes, and empirical Bayes estimators of R are obtained and their properties are studied. Confidence intervals, exact and approximate, as well as the Bayesian credible sets for R are obtained. A real example is presented in order to illustrate the inferences discussed in the previous sections. A simulation study is conducted to investigate and compare the performance of the intervals presented in this paper and some bootstrap intervals.

1. Introduction

The inverse Rayleigh distribution is an important lifetime distribution in survival analysis that has many applications in the area of reliability studies. Voda [1] presented some properties of the maximum likelihood estimator for inverse Rayleigh distribution and mentioned that the distribution of lifetimes of several types of experimental units can be approximated by the inverse Rayleigh distribution. The cumulative distribution function (cdf) of the inverse Rayleigh distribution with scale parameter λ is given by
()
The probability density function (pdf) corresponding to (1) is given by
()
We will denote inverse Rayleigh distribution with scale parameter λ by IR(λ).

In many real life applications such as meteorology, hydrology, sports, life-tests and so on, we are dealing with record values. In industry and reliability studies, many products may fail under stress. For example, a wooden beam breaks when sufficient perpendicular force is applied to it, an electronic component ceases to function in an environment of too high temperature, and a battery dies under the stress of time. But the precise breaking stress or failure point varies even among identical items. Hence, in such experiments, measurements may be made sequentially and only values larger (or smaller) than all previous ones are recorded. Data of this type are called record data. Thus, the number of measurements made is considerably smaller than the complete sample size. This measurement saving can be important when the measurements of these experiments are costly if the entire sample was destroyed.

Let {Xi, i ≥ 1} be a sequence of independent and identically distributed (iid) random variables with an absolutely continuous cumulative distribution function (cdf) F(x) and probability density function (pdf) f(x). An observation Xj is called an upper record if its value exceeds all previous observations; that is, Xj is an upper record if  Xj > Xi for every i < j. An analogous definition can be given for lower records. Records were first introduced and studied by Chandler [2]. Interested readers may refer to Arnold et al. [3], Ahmadi [4], and Gulati and Padgett [5] for more details and applications of record values.

The problem of estimating R = Pr⁡(X > Y) arises in the context of mechanical reliability of a system with strength X and stress Y and R is chosen as a measure of system reliability. The system fails if and only if, at any time, the applied stress is greater than its strength. This type of reliability model is known as the stress-strength model. This problem also arises in situations where X and Y represent lifetimes of two devices and one wants to estimate the probability that one fails before the other. For example, in biometrical studies, the random variable X may represent the remaining lifetime of a patient treated with a certain drug while Y represent the remaining lifetime when treated by another drug. The estimation of stress-strength reliability is very common in the statistical literature. The reader is referred to Kotz et al. [6] for other applications and motivations for the study of the stress-strength reliability.

The problem of estimating the stress-strength reliability Pr⁡(X > Y) in the inverse Rayleigh distribution was considered by Rao et al. [7] for ordinary samples. Soliman et al. [8] discussed different methods of estimation for the inverse Rayleigh distribution based on lower record values. Sindhu et al. [9] and Feroze and Aslam [10] considered the Bayesian estimation for the parameter of the inverse Rayleigh distribution under left censored data and under singly and doubly type II censored data, respectively. In this paper, we consider the problem of estimating the stress-strength reliability Pr⁡(X > Y) in the inverse Rayleigh distribution based on lower record values.

The rest of the paper is organized as follows. In Section 2, we discussed likelihood inference for the stress-strength reliability, while in Section 3 we considered Bayesian inference. In Section 4, we presented a real example. A simulation study is described in Section 5. Finally conclusion of the paper is provided in Section 6.

2. Likelihood Inference

Let X ~ IR(λ1) and Y ~ IR(λ2) be independent random variables. Let R = Pr⁡(X > Y) be the stress-strength reliability. Then,
()
We will consider estimating R based on lower record values on both variables. Let be a set of lower records from IR(λ1) and let be an independent set of lower records from IR(λ2). The likelihood functions are given by (Ahsanullah [11])
()
where fand F are the pdf and cdf of X ~ IR(λ1), respectively, and g and G are the pdf and cdf of Y ~ IR(λ2), respectively. Substituting f, F, g, and G in the likelihood functions and using (4), we obtain
()
It can be easily shown that the log-likelihood functions are given by
()
Differentiate above equations with respect to the parameters λ1 and λ2 and equating with zero, the maximum likelihood estimators (MLEs) of λ1 and λ2 based on the lower record values are given by
()
Therefore using the invariance properties of the maximum likelihood estimation, the MLE of R is given by
()
To study the distribution of we need the distributions of and . Consider first ; the pdf of the nth lower record value Rn is given by (Ahsanullah [11])
()
Consequently, using standard procedure of transformation of random variables, the pdf of is given by
()
This is recognized as the inverted gamma distribution; that is, Z1 ~ IGamma(n, nλ1). Similarly, the pdf of is given by
()
Thus Z2 ~ IGamma(m, mλ2). Therefore we can find the pdf of
()
Consider Z2/Z1. Note that, by the properties of the inverted gamma distribution and its relation with the gamma distribution, we have (nλ1/Z1) ~ Gamma(n, 1) and (mλ2/Z2) ~ Gamma(m, 1). Hence and . Note that, by the independence of two random quantities, we have
()
Hence, (Z2/Z1) = (λ2/λ1)F(2n,2m) has a scaled F distribution. It follows that the distribution of is that of
()
which can be obtained using simple transformation techniques. This fact can be used to construct the following (1 − α)% confidence interval for R:
()
Records are rare in practice (Arnold et al. [3]) and sample sizes are often very small; however, intervals based on the asymptotic normality of MLEs can be of interest in cases when the number of records is sufficiently large. This is because of their optimal asymptotic properties under very general conditions (Lehmann [12]). Note that as n → ∞, where (→d) denotes convergence in distribution and I−1(λ1) is the asymptotic variance given by the reciprocal of the Fisher information:
()
Similarly, as m → ∞, where . Let n → ∞ and m → ∞ such that m/n → p where 0 < p < 1; it follows that . Since
()
we have
()
where
()
A (1 − α)% approximate confidence interval for R based on this asymptotic result is given by
()
where is obtained by substituting m/n for p and the MLEs and in the asymptotic standard deviation η. In these calculations we assumed that m is the smaller sample in size and n is the larger. However, if this is not the case then the formula for the asymptotic variance in the asymptotic interval should be modified accordingly.

3. Bayesian Inference

Consider the likelihood functions of λ1 and λ2 based on the two sets of lower record values from the inverse Rayleigh distribution mentioned in previous section. These suggest that the conjugate family of prior distributions for λ1 and λ2 is the Gamma family of probability distributions:
()
where γ1, θ1, γ2, and θ2 are the parameters of the prior distributions of λ1 and λ2, respectively. Combining the prior distributions in (21), with the likelihood functions in (5), we obtain the posterior distributions of λ1 and λ2 as
()
It follows that
()
It follows that the posterior distribution of R is equal to that of (1 + CW)−1, where and
()
The Bayes estimator under squared error loss is the mean of this posterior distribution which may be approximated. A Bayesian (1 − α)% confidence interval for R is given by
()
The case of a noninformative prior can be treated similarly. One of the well-known noninformative priors is the Jeffreys prior that say, . This suggests that prior densities for λ1 and λ2 are proportional to 1/λ1 and 1/λ2, respectively. Using direct arguments one can show that and . It follows that the posterior distribution of R is equal to that of , where W ~ F(2m,2n) and . Therefore a Bayesian (1 − α)% confidence interval for R is given by
()
Now consider the case when the parameters of prior distributions are themselves unknown. We consider the conjugate prior distributions for λ1 and λ2 above when the parameters θ1 and θ2 are unknown. In the empirical Bayes model, we must estimate them. So we calculate the marginal distribution of lower records, with densities
()
Using (5) and (21), we obtain
()
It can be shown that the maximum likelihood estimators (MLEs) of θ1 and θ2 based on the marginal distributions (28) are
()
With substitution and for θ1 and θ2 in prior distributions and using similar arguments above, one can show that
()
It follows that
()
It follows that ; the empirical posterior distribution of R is equal to that of , where and . A Bayesian (1 − α)% confidence interval for R is given by
()
The construction of highest posterior density (HPD) regions requires finding the set , where kα is the largest constant such that Pr⁡(θ ∈ I) ≥ 1 − α. This often requires numerical optimization techniques. Chen and Shao [13] presented a simple Monte Carlo technique to approximate the HPD region.

4. A Real Example

In order to illustrate the inferences discussed in the previous sections, in this section, we present a data analysis for two data sets reported by Stone [14]. He reports an experiment in which specimens of solid epoxy electrical-insulation were studied in an accelerated voltage life test. For each of two voltage levels 52.5 and 57.5 kV, 20 specimens were tested. Failure times, in minutes, for the insulation specimens are given as follows.

Data Set 1. It belongs to voltage level 52.5: 4690, 740, 1010, 1190, 2450, 1390, 350, 6095, 3000, 1458, 6200, 550, 1690, 745, 1225, 1480, 245, 600, 246, 1805.

Data Set 2. It belongs to voltage level 57.5: 510, 1000, 252, 408, 528, 690, 900, 714, 348, 546, 174, 696, 294, 234, 288, 444, 390, 168, 558, 288.

We fit the inverse Rayleigh distribution to the two data sets separately. We used the Kolmogorov-Smirnov (K-S) tests for each data set to fit the inverse Rayleigh model. It is observed that for data sets 1 and 2, the K-S distances are 0.2119 and 0.2280 with the corresponding P values 0.2878 and 0.2496, respectively. Therefore, it is clear that inverse Rayleigh model fits well to both the data sets. We plot the empirical distribution functions and the fitted distribution functions in Figures 1 and 2. These Figures show that the empirical and fitted models are very close for each data set.

Details are in the caption following the image
Figure 1
Open in figure viewerPowerPoint
The empirical distribution function (dashed) and fitted distribution function for Data Set 1.
Details are in the caption following the image
Figure 2
Open in figure viewerPowerPoint
The empirical distribution function (dashed) and fitted distribution function for Data Set 2.
Next, we consider the lower record values from the above observed data as follows:
  •  

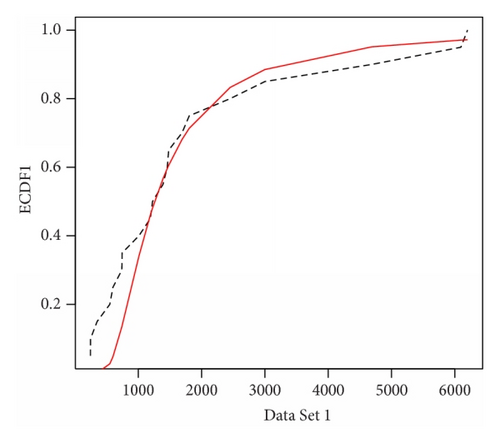
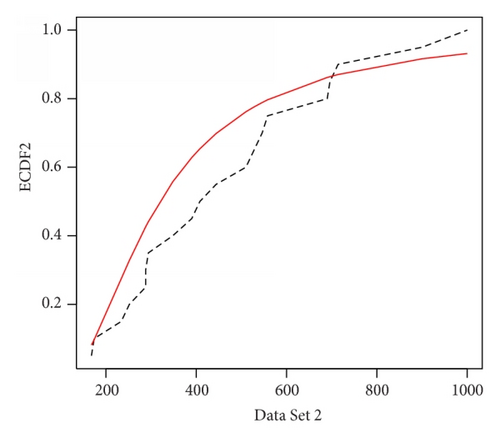
    : 4690,470,350,245,

  •  

    : 510,252,174,168.

Based on the above data, we obtain the MLEs of λ1 and λ2 as 240100 and 112896, respectively. Therefore, the MLE of R becomes . The corresponding 95% confidence interval based on (15) is equal to (0.3242, 0.9041). Letting γ1 = γ2 = 2, θ1 = 3, and θ2 = 5, the Bayesian 95% confidence interval based on (25) is equal to (0.3371, 0.8453). So, the Bayesian 95% confidence interval based on (26) is equal to (0.3242, 0.9041). Finally, the Bayesian 95% confidence interval based on (32) is equal to (0.3935, 0.8745).

5. A Simulation Study

In this section, a simulation study is conducted to investigate and compare the performance of the confidence intervals presented in this paper and some bootstrap intervals. There are several bootstrap based intervals discussed in the literature (Efron and Tibshirani [15]). It is important here to note that all inference procedures in this paper depend only on the smallest records, rn and sm. Therefore we will use the parametric bootstrap based on the marginal distribution of Rn as given in (9). In what follows we describe the bootstrapping procedure.
  • (1)

    Calculate , , and , the maximum likelihood estimators of λ1, λ2, and R based on rn and sm.

  • (2)

    Generate from the distribution given in (9) with λ1 replaced by and generate similarly.

  • (3)

    Calculate , , and using the and obtained in Step (2).

  • (4)

    Repeat Steps (2) and (3) B times to obtain .

Then we can calculate the following bootstrap intervals.
Normal Interval. The simplest (1 − α) bootstrap interval is the normal interval
()
where is the bootstrap estimate of the standard error based on .
Basic Pivotal Interval. The (1 − α) bootstrap basic pivotal confidence interval is
()
where is the β quantile of .
Percentile Interval. The (1 − α) bootstrap percentile interval is defined by
()
that is, just use the α/2 and 1 − α/2 quantiles of the bootstrap sample.

Interested readers may refer to DiCiccio and Efron [16] and the references contained therein to observe more details.

In the simulation design we used all combinations of n = 5,10,15 and m = 5,10,15. We used λ1 = 1 and R = 0.1,0.25,0.5. The value of λ2 is determined by the choice of λ1 and R. The confidence level taken is (1 − α) = 0.90 and 0.95. For each combination of the simulation indices we generated 2000 samples of lower records from the distributions of X and Y. For each generated pair of samples we calculated the following intervals:
  • (1)

    ML: the interval based on the MLE given in (15),

  • (2)

    Bayes: the interval based on the Bayes estimator given in (25),

  • (3)

    J.B: the interval based on the Bayes estimator given in (26),

  • (4)

    E.B: the interval based on the empirical Bayes estimator given in (32),

  • (5)

    Norm: the normal interval,

  • (6)

    Basic: the basic pivotal interval,

  • (7)

    Perc: the percentile interval.

The empirical coverage probability and expected lengths of intervals are obtained by using the 2000 replications. In the interval based on the Bayes estimators we used γ1 = 3, γ2 = 5, θ1 = 2, and θ2 = 4 wherever we need them. For bootstrap intervals we used 1000 bootstrap samples. The results of our simulations are given in Tables 1 and 2.

Table 1. Expected lengths and coverage rates (in parentheses) of the confidence intervals with (1 − α) = 0.95.
n m R ML Bayes J.B E.B Norm Basic Perc
5 5 0.1 0.277 (0.942) 0.406 (0.520) 0.272 (0.944) 0.190 (0.847) 0.284 (0.933) 0.276 (0.822) 0.276 (0.940)
5 5 0.25 0.451 (0.951) 0.422 (0.791) 0.453 (0.951) 0.336 (0.862) 0.461 (0.908) 0.449 (0.812) 0.449 (0.949)
5 5 0.5 0.537 (0.947) 0.434 (0.988) 0.540 (0.956) 0.414 (0.868) 0.549 (0.886) 0.536 (0.798) 0.536 (0.941)
5 10 0.1 0.220 (0.952) 0.339 (0.645) 0.217 (0.947) 0.172 (0.883) 0.257 (0.957) 0.250 (0.857) 0.250 (0.947)
5 10 0.25 0.386 (0.948) 0.377 (0.871) 0.388 (0.949) 0.314 (0.879) 0.421 (0.929) 0.413 (0.841) 0.413 (0.942)
5 10 0.5 0.482 (0.956) 0.403 (0.976) 0.482 (0.949) 0.390 (0.883) 0.489 (0.903) 0.480 (0.833) 0.480 (0.937)
5 15 0.1 0.203 (0.946) 0.300 (0.777) 0.202 (0.943) 0.164 (0.873) 0.248 (0.964) 0.241 (0.856) 0.241 (0.927)
5 15 0.25 0.367 (0.947) 0.352 (0.902) 0.365 (0.953) 0.301 (0.887) 0.410 (0.931) 0.402 (0.866) 0.402 (0.933)
5 15 0.5 0.460 (0.956) 0.386 (0.981) 0.459 (0.947) 0.375 (0.873) 0.466 (0.907) 0.458 (0.844) 0.458 (0.936)
  
10 5 0.1 0.235 (0.946) 0.361 (0.502) 0.236 (0.943) 0.164 (0.856) 0.209 (0.905) 0.204 (0.825) 0.204 (0.935)
10 5 0.25 0.406 (0.961) 0.377 (0.721) 0.403 (0.935) 0.299 (0.846) 0.383 (0.911) 0.375 (0.833) 0.375 (0.945)
10 5 0.5 0.482 (0.958) 0.388 (0.982) 0.480 (0.945) 0.374 (0.855) 0.489 (0.903) 0.480 (0.829) 0.480 (0.942)
10 10 0.1 0.178 (0.947) 0.292 (0.650) 0.175 (0.950) 0.144 (0.905) 0.181 (0.939) 0.178 (0.858) 0.178 (0.950)
10 10 0.25 0.326 (0.958) 0.328 (0.828) 0.327 (0.955) 0.275 (0.913) 0.330 (0.928) 0.326 (0.872) 0.326 (0.955)
10 10 0.5 0.405 (0.943) 0.352 (0.969) 0.405 (0.949) 0.346 (0.895) 0.409 (0.900) 0.404 (0.854) 0.404 (0.940)
10 15 0.1 0.157 (0.955) 0.252 (0.735) 0.156 (0.952) 0.135 (0.913) 0.167 (0.952) 0.164 (0.875) 0.164 (0.950)
10 15 0.25 0.297 (0.951) 0.300 (0.864) 0.296 (0.949) 0.258 (0.913) 0.307 (0.938) 0.304 (0.891) 0.304 (0.947)
10 15 0.5 0.374 (0.943) 0.333 (0.968) 0.374 (0.947) 0.328 (0.913) 0.377 (0.908) 0.373 (0.868) 0.373 (0.935)
  
15 5 0.1 0.224 (0.946) 0.339 (0.490) 0.221 (0.935) 0.151 (0.840) 0.189 (0.898) 0.185 (0.829) 0.185 (0.934)
15 5 0.25 0.386 (0.951) 0.355 (0.706) 0.386 (0.947) 0.283 (0.871) 0.353 (0.894) 0.346 (0.835) 0.346 (0.931)
15 5 0.5 0.459 (0.946) 0.367 (0.979) 0.459 (0.943) 0.354 (0.855) 0.463 (0.888) 0.455 (0.832) 0.455 (0.919)
15 10 0.1 0.160 (0.952) 0.270 (0.614) 0.162 (0.956) 0.134 (0.911) 0.154 (0.933) 0.152 (0.865) 0.152 (0.948)
15 10 0.25 0.300 (0.943) 0.304 (0.776) 0.302 (0.950) 0.256 (0.909) 0.295 (0.911) 0.291 (0.869) 0.291 (0.937)
15 10 0.5 0.374 (0.948) 0.327 (0.967) 0.375 (0.950) 0.323 (0.911) 0.378 (0.919) 0.374 (0.873) 0.374 (0.947)
15 15 0.1 0.138 (0.946) 0.229 (0.658) 0.139 (0.947) 0.122 (0.919) 0.140 (0.936) 0.138 (0.881) 0.138 (0.948)
15 15 0.25 0.266 (0.953) 0.274 (0.847) 0.267 (0.951) 0.236 (0.920) 0.268 (0.929) 0.266 (0.884) 0.266 (0.950)
15 15 0.5 0.339 (0.952) 0.305 (0.965) 0.339 (0.948) 0.303 (0.915) 0.342 (0.931) 0.339 (0.899) 0.339 (0.952)
Table 2. Expected lengths and coverage rates (in parentheses) of the confidence intervals with (1 − α) = 0.90.
n m R ML Bayes J.B E.B Norm Basic Perc
5 5 0.1 0.223 (0.890) 0.343 (0.504) 0.224 (0.895) 0.159 (0.766) 0.235 (0.900) 0.223 (0.782) 0.223 (0.890)
5 5 0.25 0.378 (0.908) 0.359 (0.632) 0.383 (0.892) 0.284 (0.775) 0.385 (0.868) 0.378 (0.768) 0.378 (0.908)
5 5 0.5 0.460 (0.897) 0.369 (0.961) 0.462 (0.912) 0.351 (0.784) 0.461 (0.832) 0.460 (0.746) 0.460 (0.895)
5 10 0.1 0.180 (0.899) 0.288 (0.650) 0.183 (0.890) 0.145 (0.804) 0.213 (0.931) 0.200 (0.819) 0.200 (0.892)
5 10 0.25 0.331 (0.910) 0.320 (0.744) 0.329 (0.901) 0.265 (0.802) 0.356 (0.894) 0.350 (0.808) 0.350 (0.892)
5 10 0.5 0.411 (0.897) 0.342 (0.951) 0.411 (0.904) 0.330 (0.799) 0.410 (0.846) 0.409 (0.778) 0.409 (0.893)
5 15 0.1 0.171 (0.895) 0.255 (0.733) 0.171 (0.895) 0.139 (0.803) 0.209 (0.936) 0.197 (0.834) 0.197 (0.879)
5 15 0.25 0.309 (0.894) 0.299 (0.797) 0.310 (0.910) 0.255 (0.837) 0.341 (0.881) 0.334 (0.819) 0.334 (0.879)
5 15 0.5 0.392 (0.900) 0.328 (0.938) 0.391 (0.902) 0.318 (0.812) 0.389 (0.845) 0.389 (0.793) 0.389 (0.883)
  
10 5 0.1 0.190 (0.890) 0.305 (0.492) 0.191 (0.907) 0.135 (0.805) 0.175 (0.869) 0.169 (0.785) 0.169 (0.889)
10 5 0.25 0.341 (0.895) 0.319 (0.588) 0.340 (0.900) 0.253 (0.795) 0.323 (0.848) 0.320 (0.796) 0.320 (0.886)
10 5 0.5 0.411 (0.900) 0.330 (0.950) 0.410 (0.899) 0.317 (0.792) 0.410 (0.852) 0.410 (0.786) 0.410 (0.892)
10 10 0.1 0.145 (0.901) 0.246 (0.611) 0.145 (0.898) 0.120 (0.834) 0.150 (0.907) 0.145 (0.832) 0.145 (0.895)
10 10 0.25 0.276 (0.897) 0.277 (0.705) 0.274 (0.905) 0.231 (0.848) 0.278 (0.885) 0.276 (0.834) 0.276 (0.898)
10 10 0.5 0.344 (0.897) 0.298 (0.934) 0.344 (0.904) 0.293 (0.835) 0.344 (0.862) 0.344 (0.825) 0.344 (0.898)
10 15 0.1 0.129 (0.899) 0.212 (0.655) 0.130 (0.900) 0.112 (0.844) 0.139 (0.913) 0.134 (0.839) 0.134 (0.900)
10 15 0.25 0.248 (0.895) 0.254 (0.750) 0.250 (0.892) 0.182 (0.853) 0.256 (0.882) 0.253 (0.834) 0.253 (0.896)
10 15 0.5 0.318 (0.903) 0.282 (0.915) 0.318 (0.896) 0.278 (0.850) 0.318 (0.876) 0.318 (0.847) 0.318 (0.904)
  
15 5 0.1 0.182 (0.913) 0.286 (0.407) 0.179 (0.898) 0.125 (0.785) 0.159 (0.878) 0.155 (0.814) 0.155 (0.897)
15 5 0.25 0.321 (0.903) 0.300 (0.530) 0.323 (0.889) 0.238 (0.763) 0.295 (0.850) 0.293 (0.800) 0.293 (0.884)
15 5 0.5 0.391 (0.893) 0.311 (0.951) 0.390 (0.884) 0.299 (0.773) 0.390 (0.841) 0.389 (0.789) 0.389 (0.878)
15 10 0.1 0.133 (0.899) 0.227 (0.501) 0.134 (0.894) 0.111 (0.836) 0.131 (0.897) 0.128 (0.844) 0.128 (0.896)
15 10 0.25 0.251 (0.881) 0.255 (0.674) 0.250 (0.891) 0.212 (0.831) 0.247 (0.865) 0.245 (0.827) 0.245 (0.888)
15 10 0.5 0.317 (0.896) 0.277 (0.935) 0.318 (0.907) 0.273 (0.852) 0.317 (0.862) 0.317 (0.820) 0.317 (0.897)
15 15 0.1 0.115 (0.899) 0.193 (0.620) 0.116 (0.904) 0.102 (0.858) 0.118 (0.913) 0.115 (0.859) 0.115 (0.898)
15 15 0.25 0.225 (0.906) 0.231 (0.738) 0.224 (0.900) 0.199 (0.852) 0.226 (0.890) 0.225 (0.858) 0.225 (0.905)
15 15 0.5 0.287 (0.901) 0.258 (0.927) 0.287 (0.905) 0.256 (0.871) 0.286 (0.872) 0.287 (0.840) 0.287 (0.898)

6. Conclusion and Discussion

Based on simulation results in Tables 1 and 2, we observe that the length of the intervals is maximized when R = 0.5 and gets shorter and shorter as we move away to the extremes. Increasing the sample size on either variable also results in shorter intervals. The performance of both basic pivotal interval and percentile interval is similar in terms of expected length but in terms of coverage rate percentile interval has the better performance. The percentile interval appears to be the best among bootstrap intervals. The interval based on the MLE and the interval based on the Bayes estimator given in (26) appear to perform almost as well as the percentile interval. The interval based on the Bayes estimator given in (25) has best coverage rate and the short expected length between the other intervals when R = 0.5, but it has the low coverage rate and the long expected length for small values of R since it is dependent on choice of θ1 and θ2 values. Furthermore, the interval based on the empirical Bayes estimator has the shortest expected length between the other intervals but it has the low coverage rate.

Based on the above discussion, we can conclude that, between the intervals obtained in this paper, the intervals based on the MLE, and the Bayes estimator given in (26) and between the bootstrap intervals, percentile interval simultaneously has the short expected length and very good coverage rate in comparison with the other intervals. Hence, we recommend using this confidence interval in all.

Conflict of Interests

The authors declare that there is no conflict of interests regarding the publication of this paper.

Acknowledgments

The authors express their sincere thanks to the editor and the referees for their constructive criticisms and excellent suggestions which led to a considerable improvement in the presentation of the paper.

      The full text of this article hosted at iucr.org is unavailable due to technical difficulties.