Journal of Atomic and Molecular Physics
Volume 2014, Issue 1 106178
Research Article
Open Access

Study of Complexation in Acetone-Chloroform Mixtures by Infrared Spectroscopy

Oleksii O. Ilchenko, 

Corresponding Author

Oleksii O. Ilchenko

Radiophysical Department, National Taras Shevchenko University of Kyiv, Volodymyrska Street 64, Kyiv, Ukraine univ.kiev.ua

Search for more papers by this author
Andrii M. Kutsyk, 

Andrii M. Kutsyk

Radiophysical Department, National Taras Shevchenko University of Kyiv, Volodymyrska Street 64, Kyiv, Ukraine univ.kiev.ua

Search for more papers by this author
Vyacheslav V. Obukhovsky, 

Vyacheslav V. Obukhovsky

Radiophysical Department, National Taras Shevchenko University of Kyiv, Volodymyrska Street 64, Kyiv, Ukraine univ.kiev.ua

Search for more papers by this author
First published: 24 February 2014
https://doi.org/10.1155/2014/106178
Academic Editor: Keli Han

Abstract

FTIR spectra of acetone-chloroform system with various component ratios were investigated within the spectral range 3950–4550 cm−1. Methods of multivariate curve resolution were applied to decompose the FTIR spectra into specific components of different composition. A method of decomposition based on structural model of solution which contains acetone, chloroform, and complex acetone/chloroform (1 : 1) was proposed. Results of both approaches are in good agreement within the range of measuring error.

1. Introduction

Acetone-chloroform mixture is a prominent example of a system with a pronounced negative deviation from ideal solution behavior. So it has been the subject of many theoretical and experimental researches [1–6]. The main problem is the structure and composition of associated species of these mixtures.

Infrared spectroscopy is powerful tool of investigation of liquid systems [7]. The IR spectra are very sensitive to structural changes caused by intermolecular interactions between components of solution. Multivariate regression can be used for the determination of quantitative information from IR spectra, such as number and concentration of species in the mixture [8].

The purpose of this work is quantitative analysis of acetone-chloroform mixture using model-free and model-based multivariate regression approaches.

2. Experiment

FTIR transmission spectra were measured with Thermo Scientific spectrometer Nicolet 6700 with a spectral resolution of 4 cm−1. Optical path length of the quartz cell was 1 mm. The heating of the sample almost did not occur during the measurements due to small value of absorption coefficient at excitation frequency. The temperature of liquid samples was 25 ± 0.2°C. The chloroform and acetone with purity 99.9% were used in this research. The concentration of components was changed from 0% to 100% (in volume %) with step 10%. Spectra recording was repeated 5 times for every sample. Thereafter the average spectra were calculated for every concentration and used in further analysis.

3. Theory

3.1. Multivariate Curve Resolution

Resolution methods decompose mathematically a global mixed instrumental response into the pure contributions due to each component in the system [9]. This mixed signal is organized in the matrix D containing raw information about all the components present in the data set. Resolution methods allow for the decomposition of the initial mixture data matrix D into the product of two data matrices C and ST, each of them including the pure response profiles of the n mixture or process components associated with the row and the column direction of the initial data matrix, respectively. In matrix notation, the expression valid for all resolution methods is
()
where D(r  ×  c) is the original data matrix, C(r  ×  n) and ST(n   ×   c) are the matrices containing the pure response profiles related to the data variation in the row direction and in the column direction, respectively, and E(r  ×  c) is the error matrix, that is, the residual variation of the data set that is not related to any chemical contribution. Parameters r and c are the number of rows and the number of columns of the original data matrix, respectively, and n is the number of chemical components in the mixture or process. C and ST often refer to concentration profiles and spectra (hence their names).
With the measurement matrix D, the problem in multivariate curve resolution is to estimate the pure variables, C and S, in terms of the bilinear model and some generic knowledge about the pure variables. Accordingly, the basic principle of curve resolution is to seek for a bilinear model that gives best fit, in the sense of least squares or weighted least squares, to the two-way data D. That is to say, one is seeking for the estimates of pure variables, C and S, which minimize the norm
()
The mathematical decomposition of a single data matrix D or, in other words, the norm minimization problem (2) is known to be subject to ambiguities [10]. This means that many sets of paired C- and ST-type matrices can reproduce the original data set with the same fit quality. But some of the obtained solutions do not have any physical meaning. In plain words, the correct reproduction of the original data matrix can be achieved by using response profiles differing in shape (rotational ambiguity) or in magnitude (intensity ambiguity) from the sought (true) ones [11]. Mathematically it can be written as follows:
()
where T(n  ×  n) is invertible matrix. If T is orthogonal matrix ambiguity is rotational. The intensity ambiguity is not a serious problem in qualitative analysis (spectral identification), but it is a serious problem in quantitative analysis. The most important is the rotational ambiguity which always occurs when there are several overlapped profiles of components. The presence of this ambiguity means that estimated spectrum for any of component will be unknown linear combination of true components spectra.

There are many methods of decomposition experimental matrix D [12]. The one of most popular techniques is Multivariate Curve Resolution-Alternating Least Squares (MCR-ALS) [9]. MCR-ALS solves iteratively (2) by an alternating least squares algorithm which calculates concentration C and pure spectra ST matrices optimally fitting the experimental data matrix D. The algorithm comprises an iterative solving of two alternating least squares problems, that is, minimization of (2) over C for fixed S as well as minimization of (2) over S for fixed C. This optimization is carried out for a proposed number of components and using initial estimates of either C or ST.

3.2. Estimation of Band Boundaries of Feasible MCR Solutions

Complete resolution of a two-way data set without ambiguities is only possible in some favorable cases where selectivity [11] or local rank conditions [13] are present. When these resolution conditions are not present in the system, resolution without ambiguities is not possible even if constraints such as nonnegativity, unimodality, or closure are applied [14]. In these cases, instead of unique profiles, a range or band of feasible profiles fitting equally well the experimental data and fulfilling the physical and chemical constraints of the system has to be considered.

Boundaries of feasible solutions are related to rotational matrices Tmin⁡,k and Tmax⁡,k for each species k. Maximum and minimum band boundaries for concentration and spectral profiles may be defined by the following equation:
()
The goal is calculation of matrices Tmin⁡,k and Tmax⁡,k for finding band boundaries. The problem is considered in frame of a constrained nonlinear optimization problem. It is described mathematically using the equation [15]
()
where f(T) is an objective function; gineq is vector of inequality constraints (such as nonnegativity, selectivity, and unimodality); ge is vector of equality constraints (mass balance, known values of concentration, etc.). Gemperline [16] and Tauler [15] have shown that the calculation of the band boundaries of feasible solutions for every species is possible when an objective optimization function is defined in terms of the ratio of the signal contribution of that species to the whole signal contribution for the mixture of all species. For example, Tauler proposed to define objective function as
()
where ck and sk are concentration and spectral profiles (column-vectors) of species k in mixture.

The method needs firstly the estimation of one of the feasible solutions within the range of all possible solutions, for instance, using alternating least squares with constraints [9]. Secondly, once this feasible solution is available, a nonlinear constrained optimization is initiated looking for the boundaries of the whole set of feasible solutions. For each component k we must solve problem (5). When the optimization is implemented as a minimization of the objective function as in (4), we will find the minimum band boundaries, whereas if the optimization is implemented as a maximization of the objective function with changed sign, we will find the maximum band boundaries functions. Implementation prior information about investigated system in form of equality and inequality constraints decreases the range of feasible solutions [15].

3.3. Model-Based Approach to Decomposition of Spectra

As it was mentioned above, multivariate curve resolution is model-free analysis and its solutions are not unique. Unlike this, model-based analysis gives unique solution and basic parameter of the process, that is, the rate constant and the equilibrium constant in equilibrium investigations [17]. Model-based approaches of fitting multivariate spectral data are based on mathematical relationships, which describe the measurements quantitatively. In chemical kinetics, the analysis is based on the kinetic model or reaction mechanism, which quantitatively describes the reactions and all concentrations in the solution under investigation. For equilibrium studies the analysis is based on the law of mass action [18].

We can use the structural model of mixture for equilibrium studies. It is well known that the dissolution of one substance in another is accompanied by the formation of molecular complexes arising due to the intermolecular interaction [19]. In the frame of the posed problem, we now consider a mixture of two molecular substances A and B in the liquid state. These components are not necessarily monomolecular. In many cases the structural forms of liquid state are dimers, trimmers, and so forth. The interaction between molecules leads to formation of complex AB (it is considered as an effective type of complex). In what follows, we will consider only the “formation-decay” reactions:
()
For the formation of the species AB, according to (7), we can write equilibrium constant Kc as follows:
()
where square brackets denote the molar concentration of species (mol/L).

If we know structural model of mixture and values of components concentrations before mixing, we can estimate the matrix of concentrations. We could get elements of matrix C by solving (8) at fixed value of Kc.

Hence, we can find the matrix of spectral profiles S:
()
Using (1) and (9), matrix of residuals can be transformed:
()
Firstly, we need to find Kc to calculate concentration profiles. Therefore, the next optimization problem should be solved:
()

4. Results and Discussion

4.1. IR Measurements

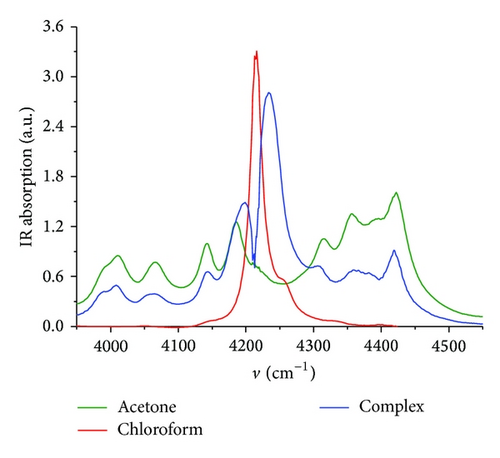
FTIR transmission spectra (Figure 1) were detected in spectral range 3950–4550 cm−1. This spectral range was chosen due to the weak absorption of overtones and composite frequencies in Near-IR region. Weak absorption value allows using the liquid cell with a relatively large value of the optical beam path (1 mm). Measurements in Mid-IR region require to use the optical beam path around 10–25 μm. Therefore, this range is not preferred for the quantitative analysis. However, the Near-IR range allows carrying out reproducible concentration analysis with relative accuracy of at least 1%.

Details are in the caption following the image
Figure 1
Open in figure viewerPowerPoint
IR absorbance spectra of acetone-chloroform mixtures with different component ratios.

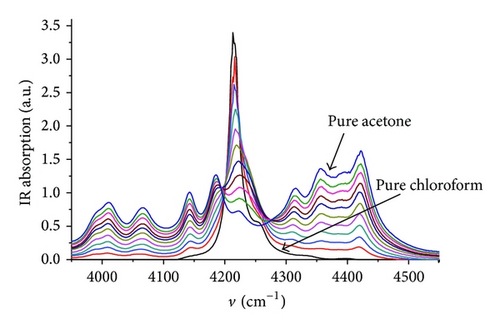
4.2. MCR-ALS Analysis

Our approach is based on a three-component MCR-ALS analysis of the FTIR spectra of water-methanol solutions. During ALS optimization nonnegativity, unimodality, and closure constraints were applied. We found that three components are required to obtain a good fit to the data (accuracy better than 1%). The “pure” components were identified as “free acetone (C3H6O)” and “free chloroform (CHCl3),” and the third component as “acetone-chloroform complex.” The graphical user interface (GUI) in the MATLAB environment developed by Jaumot et al. [20] was used for determination of concentration and spectral matrixes.

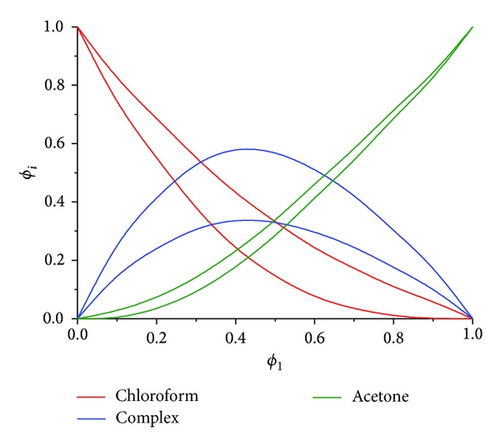
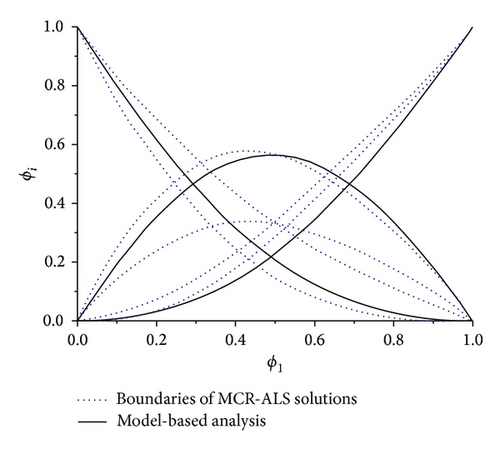
We used MCR-BANDS GUI [16] to decrease rotational ambiguity of obtained solutions; in other words it was used to solve nonlinear constrained optimization problem (5). MCR-ALS solutions were used as initial estimation and nonnegativity, unimodality, and closure constraints were also applied. The results on the resolved FTIR spectra (ST) and the concentrations (C) (band boundaries of feasible solutions) are shown in Figure 2. ϕ1 is volume fraction of acetone before mixing; ϕi,    i = A, B, and  AB, is volume fraction of species in the mixture.

Details are in the caption following the image
Figure 2 (a)
Open in figure viewerPowerPoint
Boundaries of concentration (a) and spectral profiles (b) of “pure” components obtained by MCR-BANDS analysis (ϕ1, ϕi,  i = A, B, AB: volume fraction of acetone before mixing and volume fraction of species in mixture).
Details are in the caption following the image
Figure 2 (b)
Open in figure viewerPowerPoint
Boundaries of concentration (a) and spectral profiles (b) of “pure” components obtained by MCR-BANDS analysis (ϕ1, ϕi,  i = A, B, AB: volume fraction of acetone before mixing and volume fraction of species in mixture).

4.3. Model-Based Analysis

It is possible to consider acetone-chloroform mixture as ternary. There is no doubt as to formation of equimolar complex AB [1]. The formation of AB complex explains qualitatively the negative values of the excess thermodynamic functions [2]. But there are evidences of existence of AB2 complex [3–6]. In our investigation we neglected the presence of AB2 complex due its small amount. The self-association into dimers of pure acetone and pure chloroform was taken into account. Thus, the “formation-decay” reactions become:
()
The equilibrium constant Kc is defined by the equation
()
We hold total volume of components before mixing constant:
()
where are amounts of acetone and chloroform before mixing (in mol); are molar volumes of acetone and chloroform, respectively. Change in volume after mixing is small; its maximum value is about 0.25% of molar volume of mixture [2]. So we neglected this change and considered volume of mixture as constant. Thus we can express equilibrium constant in terms of volume fractions of component:
()
where , is volume fraction of species in mixture; are amount of species and its molar volume, respectively. So in (1) matrix C consists of volume fractions of component. The relationship between fractions before and after mixing is as follows:
()
Substituting ϕA,B in (15) by (16), we obtain
()

We can obtain volume fraction of AB complex by solving (17) with known values of K  and  ϕ1, and thus we can obtain volume fraction of species A and B using (16). Matrix C can be obtained by changing values of ϕ1.

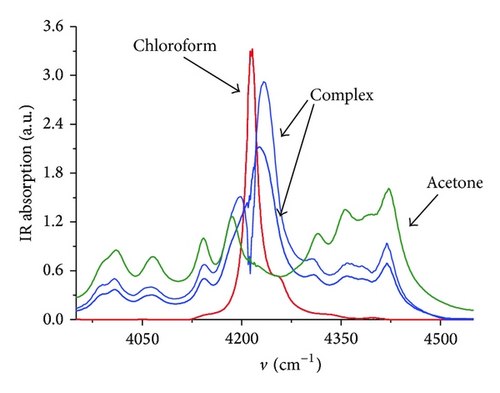
We solved (11) numerically with optimization parameter K. The optimal value is K = 6.76. In Figure 3 concentration and spectral profiles at this value of equilibrium constant are shown.

Details are in the caption following the image
Figure 3 (a)
Open in figure viewerPowerPoint
Concentration (a) and spectral profiles (b) of “pure” components obtained by model-based analysis (ϕ1, ϕi,  i = A, B, AB: volume fraction of acetone before mixing and volume fraction of species in mixture).
Details are in the caption following the image
Figure 3 (b)
Open in figure viewerPowerPoint
Concentration (a) and spectral profiles (b) of “pure” components obtained by model-based analysis (ϕ1, ϕi,  i = A, B, AB: volume fraction of acetone before mixing and volume fraction of species in mixture).

4.4. Comparison

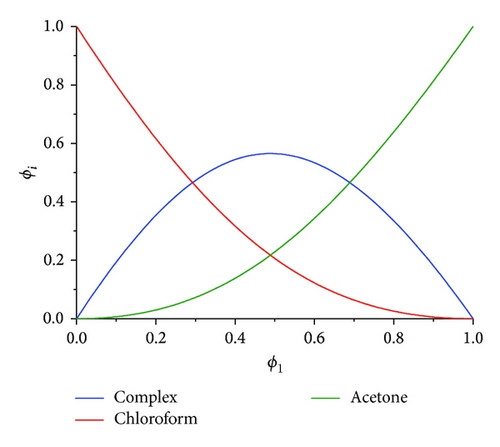
We compared the resolved results by model-based analysis concentration profiles with those obtained by MCR-ALS. The result of comparison is shown in Figure 4. The results of both approaches are in good agreement within the range of measuring error. The concentration profile of complex obtained by MCR-ALS is skew. It may be explained by existence of small amount of AB2 complex at low concentration of acetone. Because MCR-ALS analysis is model-free we do not know what type (or types) of complex forms this concentration profile. Thus complex profile in model-free analysis may be considered as integral profile of all complexes which are existent in mixture.

Details are in the caption following the image
Figure 4
Open in figure viewerPowerPoint
The result of comparison of resolved concentration profiles using model of mixture (solid curves) and boundaries of MCR solutions (dotted curves).

5. Conclusions

The analysis of FTIR spectra at different acetone concentrations in acetone-chloroform system using MCR-ALS method was carried out. It can give very necessary information about complex formation in this mixture. Three-component model of the mixture was chosen for the analysis. MCR-BANDS technique was used to obtain the band boundaries of MCR-ALS solutions.

The most difficult aspect of model-based approach is the determination of correct model. The process of fitting several models and comparing the results can be tedious. Three-component model of the mixture was used successfully for model-based approach to decomposition of spectra. Despite simplifying model usage, the concentration profiles obtained by model-free and model-based approaches are in good agreement within the range of measuring error. AB2 complex forming will be subject of our further investigation.

Both approaches should be used in decomposition liquid mixture vibrational spectra. The model-free analysis can be invaluable in supporting the model choice.

Conflict of Interests

The authors declare that there is no conflict of interests.

    The full text of this article hosted at iucr.org is unavailable due to technical difficulties.