A Driver Modeling Based on the Preview-Follower Theory and the Jerky Dynamics

1. Introduction

Although the chassis control systems of a vehicle can improve vehicle dynamics performances, enhance active safety, and reduce driver load, they bring more challenges for the evaluation of vehicle performance, especially for the evaluation of handling and stability in terms of subjective sense [1, 2]. Previous studies [3, 4] reveal that the driver-vehicle-road closed-loop system works effectively when investigating the performances of vehicle handling and stability. In order to evaluate the handling quality of a vehicle and avoid potential risk in actual tests, the study on driver modeling is essential. This research field has drawn significant attention and several typical models have been carried out by many researchers in an early time. In 1953, Kondo [5] started with driver modeling in Japan. His research is based on the 2-wheel vehicle model on a straight line, running at a constant speed with side wind disturbances. In addition, McRuer and Jex [6] extended pilot models to road driver models by considering the factors of reaction time and inertial delay and a compensation driver model was presented. However, the preview characteristics of the driver were not taken into consideration in the studies. Macadam [7] established a driver model by using optimal preview closed-loop control in 1980. Moreover, the Preview-Follower theory [8] was proposed for the purpose of modeling the driver’s path-following behaviors. The driver’s behaviors were assumed based on the path-following theory in which the driver’s operation always aims at minimizing the errors between the desired and actual vehicle trajectory [9]. With the development of intelligence technology, several artificial neural network driver models were proposed in order to accurately imitate human driving behaviors. For instance, Fujioka et al. [10] presented a NN driver model, in which the steering angle was mapped as a function of lateral deviation and heading angle. The model was trained by a human driver in a simulator environment. Neusser et al. [11] also proposed a neurocontroller for lateral vehicle guidance. This driver model was trained with measured human-driving data. In addition, Macadam and Johnson [12] constructed a two-layer neural network to represent driver steering behaviors. Sampled data collected by the sensors of an on-road car was employed to train the network. Guo et al. [13] proposed a preview optimal artificial neural network (ANN) driver model, whose training sample was the ideal following path instead of experimental data. The global optimization of the closed-loop system was carried out in the training process of the network through the Genetic Algorithm. Further research showed that the weight factors of this artificial neural network could be calculated analytically through the Error Elimination Algorithm [14]. For the sake of simulating driver behaviors under some severe or critical scenarios, Edelmann et al. [15] presented a driver model for higher lateral accelerations. The driver model was able to perform a good tracking behavior even at higher lateral accelerations. Tracking accuracy was further enhanced by incorporating information on the change of curvature and the local curvature of vehicle motion in the prediction of anticipated vehicle positions. The above-mentioned models were established based on the driver’s visual sensory inputs; kinesthetic (steering torque) or vestibular (lateral acceleration, yaw rate, and slip angle) sensory was not taken into account. Recently, some driver models were proposed in [16–18]; those models integrate both anticipatory and compensatory visual strategies and take into account both visual perception and kinesthetic perception. Little amount of the literature gives information on how vestibular information is used.

Many driver models have been established based on many kinds of modern control theories and methods. Unlike acceleration, velocity, and displacement of vehicle, the time derivative of acceleration (TDoA) of vehicle motion, which is used to show the vestibular information, has not been extensively studied in those studies. The TDoA, also referred to in the literature as jerk, is one of the parameters considered in vibration control [19] and comfort evaluation [20, 21]. It is a physical property that is felt by humans when a sudden change of motion occurs. Consequently, it is closely monitored for discomfort caused to a passenger in a vehicle. As a sudden change of motion occurs, the vehicle might drop into the boundary area of stability, and the tire forces are prone to sudden change. The driver response can be made according to the steering torque feedback and the jerk dynamics on the vehicle response to lateral force change. Thus, the optimal preview control driver model cannot achieve accurate vehicle performance, especially when the tires are in the sudden change conditions.

Hence, it is essential to consider the TDoA of vehicle motion in the preview-follower driver model. Based on the preview-follower driver modeling approach and ANN, a modified driver model considering the jerky dynamics is investigated. The drivers’ behaviors are described with the parameters of preview and jerk characteristic. The steering angle is obtained according to the error between the real track and the planned path and modified by the jerky dynamics under lateral force mutation. This paper is organized as follows. A modified driver model is presented in Section 1. Internal vehicle model is built and simplified in Section 2. The parameters of driver and vehicle characteristics are analyzed and calculated according to the driving conditions in Section 3, where road tests are used to verify vehicle model and calculate the closed-loop system parameters. Numerical simulations are employed to verify the proposed driver model in Section 4. Conclusions are given in Section 7.

2. Modeling of Driver-Vehicle System

Many driver models have been established to simulate the characteristics of driving behaviors on the desired trajectory. On the basis of the previous researches, the paper explores the driver model based on the combination of the preview-follower theory and the jerky dynamics.

2.1. Preview-Follower Theory

Preview-Follower theory describes the following properties in accordance with the future input information. The theory can be demonstrated generally with the following points.

• (1)

  Since the drivers operation is a low frequency process under usual driving, the transfer function of the closed-loop system should always be 1 at low frequency range. That is, P(s) · F(s) ≈ 1. The theory is realized by a cascade system, which is composed of a preview and a follower. P(s) and F(s) denote the preview and follower transfer functions, respectively.

• (2)

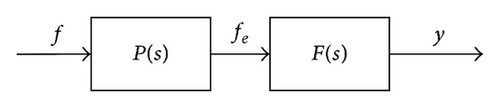
  Figure 1 shows the diagram of the preview-follower’s structure, where y denotes the vehicle’s actual lateral position and f and f_e denote the vehicle lateral position on the absolute and vehicle coordinate system, respectively [8].

2.2. Preview Optimal Simple Artificial Neural Network Driver Model

Generally, the behaviors of a qualified and excellent driver fit with the Preview-Follower theory. According to this knowledge, the preview optimal simple artificial neural network (POSANN) driver model is built in Figure 2.

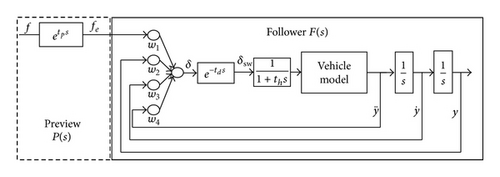
In the preview module P(s), the driver can acquire the effective road information f_e from target course f through preview process, whose transfer function is $$, in which t_p indicates the driver preview time for path following. The input f represents the function of the lateral displacement of the target course, and the output f_e indicates the lateral displacement of the target course at look-ahead point.

In the follower module F(s), the driver uses the motion information of the vehicle to decide on the optimal steering wheel angle δ. However, since there are response delays of both human and vehicle, the real steering wheel angle of vehicle should be δ_sw. w₁ ~ w₄ are the ANN weight coefficients of f_e, lateral displacement y, lateral speed $$, and lateral acceleration $$, respectively. Here, human factors are taken into account, which are expressed by the reaction delay of the driver with the transfer function $$. In this transfer function, t_d is the lag of the driver’s neural reaction system. 1/(1 + t_hs) reflects the inertial delay of the steering system.

2.3. A Modified ANN Driver Model with Jerky Dynamics

An unequivocal definition of the jerk as “the derivative of acceleration with respect to time” was given by Melchior who justifies the use of the term by referring to the physiological sensation experienced by large changes in acceleration [22]. Jerk has been used by many researchers to quantify aggressive driving behavior [23]. Based on Newton’s second law

$$ (1)

both sides of (1) with respect to time are differentiated; it can be seen that

$$ (2)

Thus, if the net external force is not constant, a system of constant mass will move with a jerk. That jerk is directly proportional to the time rate of change of the force and inversely proportional to the mass. Hence, the driver’s sense of discomfort may rise rapidly whenever there is the unpredictable lateral acceleration. Considering the motion parallel to the y-axis, let j, a_y, v_y, and y be the y-components of the jerk, acceleration, velocity, and position, respectively. According to the expression,

$$ (3)

Equation (3) was rewritten, letting a₁ = a_y0 (the acceleration at t = 0, so t₁ = 0) and a₂ = a_y (the acceleration at a time t, so t₂ = t). The average jerk equals the instantaneous jerk when the jerk is constant. So, (3) becomes

$$ (4)

so that

$$ (5)

The similarities between (5) and (6) are obvious

$$ (6)

Consider the method(s) it uses to obtain

$$ (7)

It can use the same methods (integration, area under a curve, or whatever) to derive

$$ (8)

It can be seen that it can move from a constant acceleration relationship to a constant jerk equation by replacing y by v_y, v_y by a_y, and a_y by j. With calculus and v_y = dy/dt, it is easy to obtain

$$ (9)

For the lateral motion of the vehicle, (9) was rewritten, letting y = y(t + T) (the new position of vehicle, T is a period of look-ahead time), y₀ = y(t) (the current lateral position of vehicle), v_y = y^′(t) (the current lateral speed of vehicle), a_y = y^′′(t) (the current lateral acceleration of vehicle), and j = y^′′′(t) (the jerk motion of the vehicle). Equation (9) becomes

$$ (10)

So, it is feasible to eliminate the error of trajectory caused by the variations of driving condition through compensation control of jerk characteristic between acceleration of present moment and previous moment. Based on the preview-follower driver modeling approach and ANN, this paper establishes the preview-compensation ANN (PCANN) driver model, which is shown in Figure 3. In this figure, P(s), F(s), and C(s) are the transfer functions of the preview, follower, and jerk character, respectively.

The compensator C(s) is introduced in order to simulate driver behaviors under lateral force disturbances. C(s) contains compensation gain and internal model. It is noted that C(s) will not be necessary unless there is transient and unpredictable vehicle motion. The relationship between the steering wheel change and the lateral acceleration change can be expressed as follows:

$$ (11)

In Figure 3, Δδ is the change of steering wheel. $$ is the steering wheel angle. a_yi is the lateral acceleration of the previous moment. a_ym is the lateral acceleration $$ of the present moment, which is the real response of vehicle under various operating conditions. Δα is the lateral acceleration change. K is the compensation gain. The internal model is the driver’s recognition and understanding of the vehicle, which can be obtained through vehicle model linearization under the steady-state condition of the previous moment. It means that internal model can produce the same outputs for the same inputs with vehicle under the steady-state condition. To be specific, a_yi and a_ym cancel out each other, Δα = 0 leads to Δδ = 0 under the steady-state condition. In this case, it is unnecessary for the driver to compensate control since the vehicle is at lateral steady-state. When there are variations of the driving condition or the vehicle dynamic characteristics, the performances of vehicle and internal model cannot stay the same, indicating that the internal model cannot produce the same outputs for the same inputs with vehicle under lateral force disturbances. In this condition, a_yi is different from a_ym, Δα ≠ 0, and Δδ ≠ 0. The driver may have a feeling of discomfort and then C(s) will be activated to make the necessary corrections for the steering wheel. The corrected steering wheel angle δ_sw is defined as follows:

$$ (12)

If there are more differences between a_yi and a_ym that the driver can feel, more corrections of the steering wheel angle will be made.

3. Internal Vehicle Model

Different vehicles lead to different second order systems. Based on step test data, the parameters (T₁, T₂, T_y1, and T_y2) of the second order system were identified by LSM (Least-Square Method) in this paper.

4. Parameters of Closed-Loop System

In this section, the parameters of closed-loop system are calculated with regard to the test data and road condition. Those parameters represent common behaviors of the driver and vehicle, including the preview time t_p, neural reaction time t_d, and inertial delay t_h of steering system. In a real world application, most of those parameters are uncertain factors. The H∞ control and robust control have been also paid considerable attention to eliminate the impact of uncertainty [26–28], According to some particular parameters values, we can obtain the weighting parameters of the driver model by the Error Elimination Algorithm. The meaning and features of each parameter will be described in detail in the following part.

4.1. Preview Time t_p

Preview time t_p can be considered mathematically as a negative delay time, which can compensate the delay characteristics of the driver and vehicle, and is one of the key parameters to express the characters of drivers. It relates not only to the driver’s characteristic but also to the driving condition. The computational method of preview time was not given in the optimal preview control driver model under complicated operation conditions [29]. The preview time is set by a time constant, and the range of values selected for the general driver model is 0.5 to 2.0 s. The fixed preview time driver models have a good tracking reference trajectory when the speed of the vehicle is low and lateral motion is not in the nonlinear area. Under high speed, complex trajectory, and bounded constraint conditions, it is difficult to complete the driving tasks for the fixed preview time driver models. When the vehicle runs from a small curvature path into a big curvature path or the vehicle speed becomes faster, the driver may reduce the preview time instinctively. Hence, t_p is related to the curvature and vehicle speed. In the big curvature path and high speed, t_p is small, and vice versa. Define that the curvature of the follow path y = f(x) is ρ and the speed is v_x. The preview time can be expressed as t_p = f(v_x, ρ). The calculation schematic diagram of preview time is shown in Figure 4. In Figure 4, OXY and O^′X^′Y^′ are the global coordinate system and vehicle coordinate system, respectively. The trajectory y = f(x) in OXY can be transformed into y^′ = g(x^′) in O^′X^′Y^′. Whether the vehicle is safe within the range of preview or deviates from the planned trajectories is an important criterion for a driver after preview time t_p. The offset τ between the vehicle driving prediction route and the center of the path can be determined by the driver’s characteristic, which is acceptance of course error for a driver. We can define the point of the maximum offset in the range of vision as the preview point of driver. When the offset reaches maximum value, which is constant for one driver, the driver will operate the steering wheel to reduce the offset and make vehicle run into a safe area. The preview distance L is defined from driver position to preview point. In Figure 4, $$ and $$. Since the radius of the desired path R = 1/ρ is much larger than that of τ, AB ≈ R + τ. Because ABO^′ is a right-angled triangle, we can obtain that

$$ (14)

According to the previous equation, the preview time can be expressed as

$$ (15)

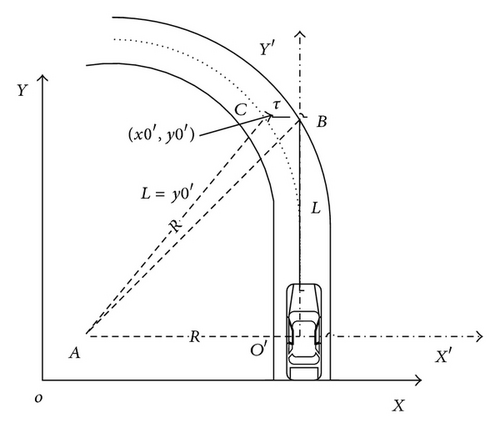
Through the above analysis, it has been seen that τ has an influence on the key parameter t_p. The value of τ can be measured through the road test as shown in Figure 4. t_p can be estimated based on (15).

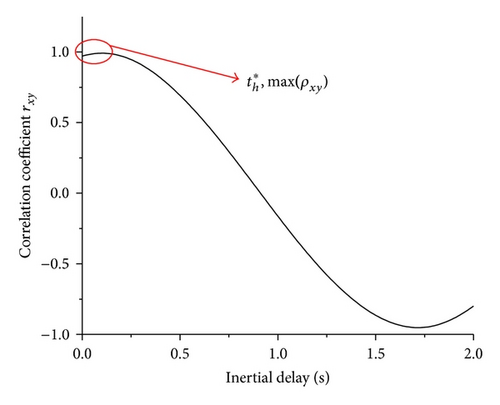
4.3. Inertial Delay t_h

This paper proposes the cross-correlation method to calculate the inertial delay t_h which is an important parameter between steering wheel and vehicle response. Generally, for single-input-single-output system, the signals of input and output are utilized to find out the largest cross-correlation and consequently calculate the time delay between input and output. In this paper, the cross-correlation R_xy between the steering wheel angle x(t) and yaw rate y(t + t_h) is achieved to calculate the inertial delay t_h, as shown in (18). The values of x(t) and y(t + t_h) are measured by the road tests, as shown in Figure 5. Consider the following:

$$ (18)

In (19), the cross-correlation coefficient can be expressed as a function of t_h as follows:

$$ (19)

where μ_x, μ_y are the arithmetic means of x(t) and y(t + t_h), respectively. σ_x, σ_y are the variances of x(t) and y(t + t_h), respectively. The curve of ρ_xy(t_h) is shown in Figure 6. When ρ_xy(t_h) reaches its largest value, t_h is equal to the steering system delay time $$, as follows:

$$ (20)

5. Test Identification and Model Verification

In order to obtain the model parameters, a lot of experiments have been carried out using a small car as test vehicle. Furthermore, the vehicle model will be verified to ensure the effectiveness of vehicle model in simulations.

5.1. Vehicle Model Verification

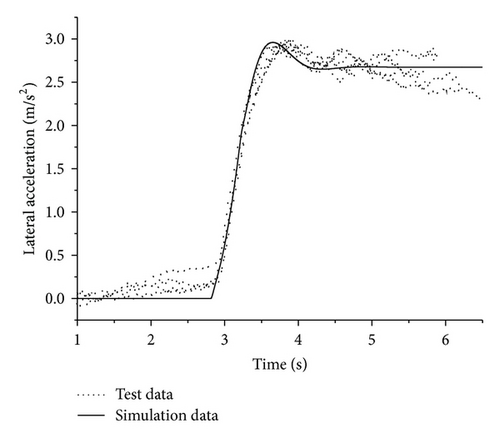
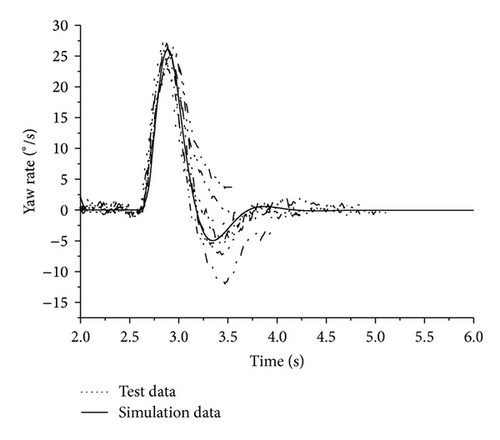
The simulations are carried out in CarSim, in which complex vehicle model can be built up to operate in nonlinear region. The vehicle model is verified by comparing the simulations and test results. Two typical tests including step input and pulse input of steering wheel angle are presented and shown in Figures 7 and 8, respectively. From the figures it can be seen that the simulation results fit the test results well, indicating that the vehicle model can be used in simulation with sufficient accuracy.

5.2. Calculation of Model Parameters

(1) The Offset τ. Based on Section 4.1, the road tests are carried out to calculate the offset τ. Typical driver A is selected for road tests. Driver A is skilled and professional with high driving proficiency. In the tests, the initial positions of the steering wheel change and speed had been recorded when the driver saw the first bend and intended to enter the bend. The offset τ was calculated and the average of results is 0.843 m.

(2) Simple Reaction Time T. In order to get actual simple reaction time T of drivers, the tests are carried out in a proving ground, in which the environmental distraction can be eliminated. The test method is to record the procedure of simple stimuli-human reaction-execution behavior using a high-speed digital camera. The test system is composed of a test car, a camera, a signal lamp, and a data collector, as shown in Figure 9. The camera is Redlake Y3 high-speed digital camera, which can provide very high sample frequency up to 2000 fps. Eight men and one woman are selected to complete this test. During the test, each subject sits in the stationary vehicle and observes the signal light. Once the signal lamp is lighted, the subject should turn the steering wheel immediately. Meanwhile, the camera records the whole process of the steering wheel operation. The time difference from the time when the signal lamp is lighted to the time when the subject starts to turn the steering wheel is the simple reaction time T. Each subject should complete the test 10 times, and the average value of these data is taken as the final result. All test results are presented in Table 1.

Table 1. Simple reaction time T of nine subjects (unit: ms).

Test number	Subjects
	1	2	3	4	5	6	7	8	9
1	257	439	279	247	280	450	408	267	244
2	256	466	271	255	271	269	—	245	237
3	—	293	249	242	265	239	284	225	293
4	263	257	242	260	263	258	381	219	332
5	273	281	253	279	338	240	341	211	268
6	314	266	295	276	277	273	—	280	273
7	267	315	241	253	338	236	373	260	265
8	284	313	293	228	377	245	306	198	260
9	—	248	285	281	256	234	296	186	280
10	314	244	266	274	286	241	353	290	258
Average T	276	302	267	261	290	250	341	238	271

(3) Inertial Delay t_h. According to Figure 5, (19), and (20), the delay time of the steering system is determined by the maximum value of ρ_xy. When the value of the correlation coefficient becomes the max value, ρ_xy = 0.98727, the value of the corresponding horizontal axis is inertial delay, t_h =  0.12 s.

6. Simulation Results and Analysis

In order to examine the influence of driver model with the jerky dynamics, the comparisons are made in several cases by simulations for the driver models with/without the compensator using the identified vehicle parameter. Here, taking the skilled driver A as an example, simulation tests are conducted in CarSim. Two emergency cases and results are described as follows.

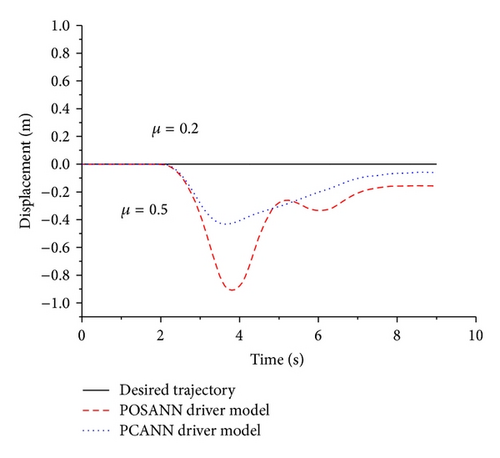
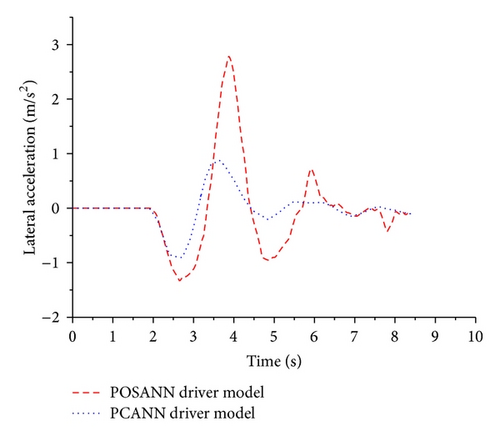
Case 1. The vehicle runs at the speed of 40 km/h on a μ-split road without ABS, which has two different friction coefficients on the left/right sides of the road center line, that is, 0.2 and 0.5. After 2 s, braking is exerted till the vehicle stops completely. The lateral displacement and acceleration of vehicle are shown in Figures 10 and 11, respectively. POSANN driver model cannot achieve accurate path following, while the PCANN driver model produces better path-following performance, considering the y-coordinate error and the lateral acceleration error. The maximum position error is 0.936 m with the POSANN driver model. Meanwhile, the maximum error obtained with the PCANN driver model is 0.435 m, which is 46.5% of that of POSANN driver model. The maximum lateral acceleration error with the POSANN driver model is 2.83 m/s². Meanwhile, the corresponding error, 32.4% of that of the POASNN driver model, is 0.918 m/s² with the POSANN driver model. Obviously, it can be seen that the PCANN driver model of the driver A can reduce vehicle lateral responses effectively and make the vehicle recovering to the stable condition much more quickly than POSANN driver model.

Case 2. In order to simulate extreme working conditions, the double-lane change is carried out in CarSim, supposing that the vehicle runs at the speed of 80 km/h into the slippery road of μ = 0.2, and the other conditions are under ideal conditions. The responses of lateral displacement and acceleration are shown in Figures 12 and 13, respectively. From these two figures, it can be obtained that the vehicle with the PCANN driver model has better performance of the lateral acceleration and the lateral displacement than that the POSANN driver model. The sway of the vehicle with the PCANN driver model is smaller than that the POSANN driver model. It is obvious that the PCANN driver model of driver A can adapt to environmental changes more rapidly.

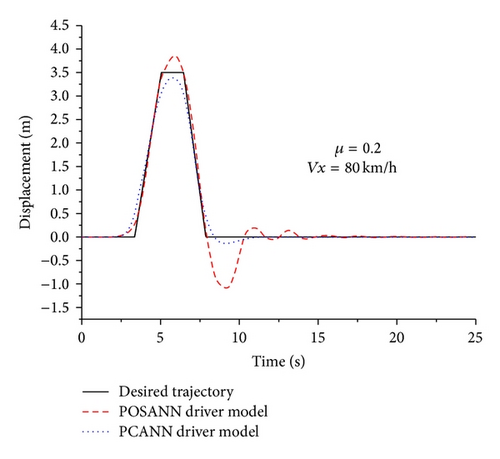
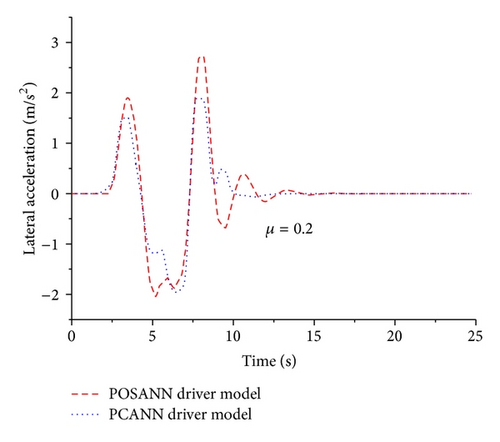
The above results in two emergency cases show that compared with the POSANN driver model, the proposed PCANN driver model can adapt to the changes of road condition more quickly, implying that the driving compensation is very necessary especially in emergency cases for the driver. The compensator will exhibit more potential benefits when the road is worse.

7. Conclusion

A new POSANN-based driver model with compensator controller using the jerky dynamics is investigated. The compensator controller is built using linearized models of the nonlinear vehicle dynamics and vehicle current states to generate a steering corrected value for the POSANN driver model. The key model parameters reflecting the driving behaviors, such as preview time and reaction time, are calculated according to the test data which can vary with changes under operating conditions. The inertial delay of the steering system is obtained by the cross-correlation method, which is applied to eliminate random fluctuation of experimental data. Simulation results demonstrated that the proposed driver model can achieve better path-following performance than the POSANN driver model under critical maneuvering conditions. Furthermore, the driver model can be used effectively for representing driver steering control behaviors to some extent. Consequently, the proposed driver model presented in this study can be used in a closed-loop simulation and in the development of the vehicle’s intelligent safety system.