Let K be a nonempty compact convex subset of a topological vector space. In this paper-sufficient conditions are given for the existence of x ∈ K such that F(T)∩VEP(F) ≠ ∅, where F(T) is the set of all fixed points of the multivalued mapping T and VEP(F) is the set of all solutions for vector equilibrium problem of the vector-valued mapping F. This leads us to generalize and improve some existence results in the recent references.

1. Introduction

Let X be a Hausdorff topological vector space, a fixed point of such a multi-valued mapping T : X → 2^X, where 2^X denotes, the family of subsets of X means a point p in X such that p ∈ T(p) and the set of all fixed points of T is denoted by F(T). The study of fixed point theorems of multi-valued mappings started from von Neumann [1] in case of continuous mappings to multi-valued mappings. Since then, various notions of the fixed point theorems for the multi-valued mappings have been studied in [2–4]. Recently, the fixed point theorems for multi-valued mapping were generalized and improved by many authors: see, for example, [5–10].

On the other hand, the equilibrium problems were introduced by Blum and Oettli [11] and by Noor and Oettli [12] in 1994 as generalizations of variational inequalities and optimization problems. The equilibrium problem theory provides a novel and united treatment of a wide class of problems which arise in economics, finance, image reconstruction, ecology, transportation, network, elasticity, and optimization. This theory has had a great impact and influence in the development of several branches of pure and applied sciences. Classical examples of equilibrium problems are variational inequalities, optimization problems, and complementarity problems. Presently, many results on the existence of solutions for vector variational inequalities (in short, VVI) and vector equilibrium problems (in short, VEP) have been established (see, e.g., [13–20]). For the more generalized from of (VEP) and (VVI) as special case, we assume that X and Y are Hausdorff topological vector spaces, K is a nonempty convex subset of X, and C is a pointed closed convex cone in Y with int C ≠ ∅. Let T : K → 2^K be a set-valued mapping and for a given vector valued mapping F : K × K → Y such that F(x, x) = 0 for each x ∈ K, the vector quasi-equilibrium problem (VQEP) and the vector quasi-variational inequality (VQVI), respectively: find x ∈ K such that

()

where A : K → L(X, Y), and L(X, Y) is denoted by the space of all continuous linear operators for X to Y: see, for example, [21–26] and references therein.

From our mentions on the importance of the fixed point theorems and the equilibrium problems, we have an inspired question to find when the set of the solution of both problems will have a joint solution, not an empty set.

To answer the question, we assume that T : K → 2^K is a set-valued mapping and for a given vector-valued mapping F : K × K → Y such that F(x, x) = 0 for each x ∈ K, let us present the fixed point problem of multi-valued mapping together with the vector equilibrium problem; in particular, it is to find x ∈ K such that

()

This problem shows the relationship in sense of intersection between fixed points of the multi-valued mapping and the vector equilibrium problem so the set of all solutions of the problem (2) is denoted by F(T)∩VEP(F). This problem includes vector quasi-equilibrium problems (in short, VQEP) and vector quasi-variational inequalities (in short, VQVI) as special cases.

The main purpose of this paper, we provide sufficient conditions and prove the existence solutions of intersection between the set of all fixed points of the multi-valued mapping and the set of all solutions for vector equilibrium problem by using the generalization of the Fan-Browder fixed point theorem. We also study the existence solutions of intersection between the set of all fixed points of the multi-valued mapping and the set of all solutions for vector variational inequality. Consequently, our results extend the existence theorems of vector quasi-equilibrium problems and vector quasi-variational inequalities.

2. Preliminaries

Throughout this paper, unless otherwise specified, we assume that X, and Y are Hausdorff topological vector spaces, K is a nonempty convex subset of X and C is a pointed closed convex cone in Y with int C ≠ ∅. From problem (2), some special cases are as follows.

(I) If T(x) ≡ K for all x ∈ K, then problem (2) reduces to the vector equilibrium problem (in short, VEP): find x ∈ K such that

()

The set of all solutions for vector equilibrium problem is denoted by VEP(F).

Moreover, if we set Y = ℝ and C = [0, ∞), then VEP reduces to the equilibrium problem that the set of all solutions is denoted by EP (F): find x ∈ K such that

()

(II) If Y = ℝ and C = [0, ∞), then problem (2) reduces to the problem: find x ∈ K such that

()

Moreover, this problem includes the quasi-equilibrium problems (in short, QEPs) considered and studied by Lin and Park [27] which is to find x ∈ K such that

()

(III) If F(x, y) = 〈Ax, y − x〉 for all x, y ∈ K, problem (3) reduces to the vector variational inequality (in short, VVI): find x ∈ K such that

()

The solution sets of problem (7) is denoted by VVI(K, A), where A : K → L(X, Y), and L(X, Y) is denoted by the space of all continuous linear operators for X to Y.

Furthermore, if Y = ℝ and C = [0, ∞), then VVI reduces to the variational inequality that the set of all solutions is denoted by VI (K, A): find x ∈ K such that

()

(IV) If F(x, y) = 〈Ax, y − x〉 for all x, y ∈ K, then problem (2) reduces to the following problems that is to find x ∈ K such that

()

This problem shows the relationship in sense of intersection between fixed points of the multi-valued mapping and the vector variational inequality so the set of all solutions of the problem (9) is denoted by F(T)∩VVI(K, A).

Let us recall some concepts and properties that are needed in this sequel. Given the multi-valued mappping T : X → 2^Y, the inverse T⁻¹ of T is the multi-valued map from ℛ(T), the range of T, to X defined by

()

The mapping f : X → Y is continuous at some point x ∈ X if and only if for any neighborhood V of f(x), there is a neighborhood U of x such that f(U)⊆V.

Definition 1 (see [28].)Let X and Y be topological vector spaces. Let K be a nonempty subset of X and C be a point closed convex cone in Y with int C ≠ ∅, where int C denotes the topological interior of C. A bifunction F : K × K → Y is said to be C-strongly pseudomonotone if, for any x, y ∈ K,

()

A mapping f : K → Y is said to be C-convex if for all x, y ∈ K and for all λ ∈ [0,1],

()

And the mapping f is said to be hemicontinuous if, for all x, y ∈ K and for all λ ∈ [0,1],

()

Remark 2. If Y = ℝ and C = [0, ∞), then

(1)
the C-strongly pseudomonotonicity of F : K × K → Y reduces to the monotonicity of F : K × K → ℝ (i.e., F(x, y) + F(y, x) ≤ 0 for all x, y ∈ K). In fact, F(x, y)∉−C∖{0}⇔F(x, y) ≥ 0, this implies that −F(y, x) ≥ 0 and it is equivalence to F(y, x)∈−C;
(2)
the C-convexity of f : K → Y reduces to the convexity of f : K → ℝ (i.e., f(λx + (1 − λ)y) ≤ λf(x)+(1 − λ)f(y)).

Definition 3 (see [29].)Let X be a topological space and let Y be a set. A map T : X → 2^Y is said to have the local intersection property if for each x ∈ X with T(x) ≠ ∅ there exists an open neighborhood V(x) of x such that ⋂_z∈V(x) T(z) ≠ ∅.

The following lemma is useful in what follows and can be found in [30].

Lemma 4. Let X be a topological space and let Y be a set. Let T : X → 2^Y be a map with nonempty values. Then, the following are equivalent.

(i)
T has the local intersection property.
(ii)
There exists a map F : X → 2^Y s.t. F(x) ⊂ T(x) for each x ∈ X, F⁻¹(y) is open for each y ∈ Y and X = ⋃_y∈Y F⁻¹(y).

Subsequently, Browder [2] obtained in 1986 the following fixed point theorem.

Theorem 5 (Fan-Browder fixed point theorem). Let X be a nonempty compact convex subset of a Hausdorff topological vector space and T : X → 2^X be a map with nonempty convex values and open fibers (i.e., for y ∈ Y, T⁻¹(y) is called the fiber of T on y). Then T has a fixed point.

The generalization of the Fan-Browder fixed point theorem was obtained by Balaj and Muresan [31] in 2005 as follows.

Theorem 6. Let X be a compact convex subset of a t.v.s and T : X → 2^X be a map with nonempty convex values having the local intersection property. Then T has a fixed point.

3. Main Theorem

In this section, the existence solutions of the fixed point for multi-valued mappings and the vector equilibrium problems will be presented. To do this, the following lemma is necessary.

Lemma 7. Let K be a nonempty and convex subset of X. Let T : K → 2^K be a set-valued mapping such that for any x ∈ K, T(x) is nonempty convex subset of K. Assume that F : K × K → Y be a hemicontinuous in the first argument, C-convex in the second argument, and C-strong pseudomonotone. Then the following statements are equivalent.

(i)
Find x ∈ K such that x ∈ T(x) and F(x, y) ∉ −C∖{0} ∀ y ∈ K.
(ii)
Find x ∈ K such that x ∈ T(x) and F(y, x) ∈ −C ∀ y ∈ K.

Proof. (i)→(ii) It is clear by the C-strong pseudomonotone.

(ii)→(i) Let x ∈ K such that

()

For any y ∈ K and α ∈ (0,1), we set z_α = αy + (1 − α)x and so we have z_α ∈ K because K is convex. By the assumption, we conclude that

()

Since F is C-convex in the second argument and by (15), we get

()

This implies that αF(z_α, y) ∈ C and since C is a convex cone then we have F(z_α, y) ∈ C. Since F is a hemicontinuous in the first argument and z_α → x as α → 0⁺, we have F(x, y) ∈ C for all y ∈ K. Therefore we obtain that

()

This completes the proof.

Theorem 8. Let K be a nonempty compact convex subset of X and let F : K × K → Y be a C-strong pseudomonotone, hemicontinuous in the first argument and C-convex, l.s.c. in the second argument such that 0 = F(x, x) for all x ∈ K. Let T : K → 2^K be a set-valued mapping such that for any x ∈ K, T(x) is nonempty convex subset of K and for any y ∈ K, T⁻¹(y) is open in K. Assume the set P : = {x ∈ X∣x ∈ T(x)} is open in K and for any x ∈ K, T(x)∩{y ∈ K | F(y, x)∉−C} ≠ ∅. Then F(T)∩ VEP (F) ≠ ∅.

Proof. For any x ∈ K, we define the set-valued mapping A, B : K → 2^K by

()

Also, we define the set-valued mapping H : K → 2^K by

()

Then we have H(x) is convex. Indeed, let y₁, y₂ ∈ B(x) and α ∈ (0,1). Since F is C-convex in the second argument, we have

()

Then αy₁ + (1 − α)y₂ ∈ B(x) and hence B(x) is convex. Since T(x) is convex, then H(x) is also convex.

By the defining of H, we see that H has no fixed point Indeed, suppose that there is x ∈ K such that x ∈ H(x). It is impossible for x ∈ K∖P, then x ∈ P and so x ∈ B(x). Thus F(x, x)∈−C∖{0}, a contradiction with 0 = F(x, x). Using the contrapositive of Theorem 6, we obtain that H has no local intersection property. Define the set-valued mapping G : K → 2^K by

()

From the C-strong pseudmonotonicity of F, we have G(x)⊆H(x) for any x ∈ K. Next, we will show that for each y ∈ K, G⁻¹(y) is open in K. For any y ∈ K, we denote the complement of A⁻¹(y) by [A⁻¹(y)] ^C = {x ∈ K∣F(y, x)∈−C}. Since C is closed and F is l.s.c. in the second argument, we have [A⁻¹(y)] ^C is closed in K and so A⁻¹(y) is open in K. We note that

()

Since for any y ∈ K, T⁻¹(y), A⁻¹(y), and P are open, we have G⁻¹(y) is open in K. Thus, by the contrapositive of Lemma 4, we have

()

Hence, there exists

such that

for all y ∈ K. That is

. If

then A(x)∩T(x) = ∅, which contradicts with the assumption. Therefore,

and A(x) = ∅. This implies that

and F(y, x)∈−C for all y ∈ K. This completes the proof by Lemma 7.

The following example guarantees the assumption that the set T(x)∩A(x) ≠ ∅, where A(x) = {y ∈ KF(y, x) ∉ −C}.

Example 9. Let X, Y = ℝ, K = [−1,1], and C = [0, ∞). For any x, y ∈ K, we define two mappings F : K × K → 2^Y and T : K → 2^K by

()

Clearly, T(x) is nonempty convex subset of K and T⁻¹(y) is open in K. If F(x, y) ∉ −C∖{0} for all x, y ∈ K, then x ≥ y and it implies that for x ≥ y, F(x, y)∈−C. This shows that F is C-strong pseudomonotone. Let x, y₁, y₂ ∈ K and α ∈ [0,1] and since 0 ∈ K, we obtain that

()

Then F is C-convex in the second argument and it is easy to see that F is a hemicontinuous in the first argument and l.s.c. in the second argument.

Note that

()

If −1 ≤ x ≤ 0, then T(x) = (−1 − x, 1] which includes (0,1]. Also (0,1] is contained A(x) for all −1 ≤ x ≤ 0. Otherwise, (x, 1]⊆(x − 1,1] for any 0 ≤ x < 1. This is to confirm the set T(x)∩A(x) ≠ ∅ for each x ∈ K (see Figure 1). Moreover, this example asserts that the set P = {x ∈ X∣x ∈ T(x)} is open in K because it is equal to the set (−0.5,1] which is open in K.

Description unavailable — **Figure 1**
Open in figure viewer PowerPoint

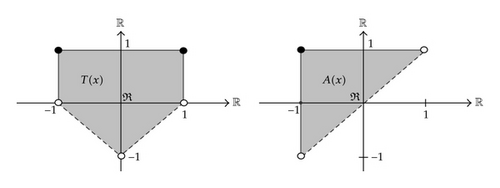
Taking T(x) ≡ K for all x ∈ K in Theorem 8, we have the following results.

Corollary 10. Let K be a nonempty compact convex subset of X and F : K × K → Y be a C-strong pseudomonotone, hemicontinuous in the first argument and C-convex, l.s.c. in the second argument such that 0 = F(x, x) for all x ∈ K. Then, VEP has a solution.

If we set the vector-valued mapping F ≡ 0, then Theorem 8 reduces to the following corollary introduced by Browder (see [2, Theorem 1]).

Corollary 11. Let K be a nonempty compact convex subset of X. Let T : K → 2^K be a set-valued mapping such that for any x ∈ K, T(x) is a nonempty convex subset of K and for any y ∈ K, T⁻¹(y) is open in K. Then there exists in K such that .

If we set Y = ℝ and C = [0, ∞) in Theorem 8 together with Remark 2, we have the following result.

Corollary 12. Let K be a nonempty compact convex subset of X and let F : K × K → ℝ be a monotone, hemicontinuous in the first argument and convex, l.s.c. in the second argument such that 0 = F(x, x) for all x ∈ K. Let T : K → 2^K be a set-valued mapping such that for any x ∈ K, T(x) is a nonempty convex subset of K and for any y ∈ K, T⁻¹(y) is open in K. Assume the set P : = {x ∈ X∣x ∈ T(x)} is open in K and for any x ∈ K, T(x)∩{y ∈ K∣F(y, x) > 0} ≠ ∅. Then F(T)∩EP (F) ≠ ∅.

Let L(X, Y) be a space of all linear continuous operators from X to Y. A mapping A : K → L(X, Y) is said to be C-strong pseudomonotone if it satisfies

()

and it is called hemicontinuous if, for all x, y ∈ K and for all λ ∈ [0,1], the mapping λ ↦ 〈T(x + λ(y − x), z)〉 is continuous at 0⁺.

As a direct consequence of Theorem 8, we obtain the following result.

Theorem 13. Let K be a nonempty compact convex subset of X and let A : K → L(X, Y) be a C-strong pseudomonotone and hemicontinuous. Let T : K → 2^K be a set-valued mapping such that for any x ∈ K, T(x) is nonempty convex subset of K and for any y ∈ K, T⁻¹(y) is open in K. Assume the set P : = {x ∈ X | x ∈ T(x)} is open in K and for any x ∈ K, T(x)∩{y ∈ K | 〈A(y), x − y〉∉−C} ≠ ∅. Then there exists such that

()

Proof. We define the vector value mapping F : K × K → Y by

()

We will show that F satisfies all conditions in Theorem 8. Clearly F(x, x) = 0 and by the assumptions of A, we have F is C-strong pseudomonotone and hemicontinuous in the first argument. Let x ∈ K be fixed. For any y, z ∈ K and θ ∈ [0,1], we obtain that

()

Then F is C-convex in the second argument.

Next, we will show that F is l.s.c. in the second argument. Let x ∈ K be fixed. Let y₀ ∈ K and N be a neighborhood of F(x, y₀). Since the linear operator Ax is continuous, there exists an open neighborhood M of y₀ such that for all y ∈ M, 〈Ax, y − x〉 ∈ N because N is a neighborhood of 〈Ax, y₀ − x〉. Thus for all y ∈ M, F(x, y) ∈ N. Hence, F is continuous in the second argument and so it is l.s.c. in the second argument. Then all hypotheses of the Theorem 8 hold and hence, there exists such that

()

This completes the proof.

If we take T(x) ≡ K for all x ∈ K in Theorem 13, we have the following corollary.

Corollary 14. Let K be a nonempty compact convex subset of X and let A : K → L(X, Y) be a C-strong pseudomonotone and hemicontinuous. Then, VVI has a solution.

If we set Y = ℝ and C = [0, ∞) in Theorem 13, we have the following result.

Corollary 15. Let K be a nonempty compact convex subset of X and let A : K → L(X, ℝ) be a monotone and hemicontinuous in the first argument. Let T : K → 2^K be a set-valued mapping such that for any x ∈ K, T(x) is a nonempty convex subset of K and for any y ∈ K, T⁻¹(y) is open in K. Assume the set P : = {x ∈ X∣x ∈ T(x)} is open in K and for any x ∈ K, T(x)∩{y ∈ K∣〈A(y), x − y〉>0} ≠ ∅. Then F(T)∩VI (K, A) ≠ ∅.

Remark 16. (1) Theorems 8 and 13 are the extensions of vector quasi-equilibrium problems and vector quasi-variational inequalities, respectively.

(2) If X is a real Banach space, then Corollary 10 comes to be Theorem 2.3 in [28].

Acknowledgment

The first author would like to thank the Office of the Higher Education Commission, Thailand for supporting by a grant fund under the program Strategic Scholarships for the Join Ph.D. Program Thai Doctoral degree for this research under Grant CHE-Ph.D.-SW-RG/41/2550, Thailand.

References

1 von Neumann J., Über ein ökonomisches Gleichungssystem und eine Verallgemeinerung des Brouwerschen Fixpunktsatzes, Ergebnisse eines Mathematischen Kolloquiums. (1937) 8, 73–83.
Google Scholar
2 Browder F. E., The fixed point theory of multi-valued mappings in topological vector spaces, Mathematische Annalen. (1968) 177, 283–301, MR0229101, https://doi.org/10.1007/BF01350721, ZBL0176.45204.
10.1007/BF01350721
Web of Science® Google Scholar
3 Fan K., Fixed-point and minimax theorems in locally convex topological linear spaces, Proceedings of the National Academy of Sciences of the United States of America. (1952) 38, 121–126, MR0047317, https://doi.org/10.1073/pnas.38.2.121, ZBL0047.35103.
10.1073/pnas.38.2.121
CAS PubMed Web of Science® Google Scholar
4 Kakutani S., A generalization of Brouwer′s fixed point theorem, Duke Mathematical Journal. (1941) 8, 457–459, MR0004776, https://doi.org/10.1215/S0012-7094-41-00838-4, ZBL0061.40304.
10.1215/S0012-7094-41-00838-4
Google Scholar
5 Du W. S., New cone fixed point theorems for nonlinear multi-valued maps with their applications, Applied Mathematics Letters. (2011) 24, no. 2, 172–178, https://doi.org/10.1016/j.aml.2010.08.040, MR2735136, ZBL1218.54037.
10.1016/j.aml.2010.08.040
Web of Science® Google Scholar
6 Hussain N. and Khamsi M. A., On asymptotic pointwise contractions in metric spaces, Nonlinear Analysis: Theory, Methods & Applications. (2009) 71, no. 10, 4423–4429, https://doi.org/10.1016/j.na.2009.02.126, MR2548672, ZBL1176.54031.
10.1016/j.na.2009.02.126
Web of Science® Google Scholar
7 Klim D. and Wardowski D., Fixed point theorems for set-valued contractions in complete metric spaces, Journal of Mathematical Analysis and Applications. (2007) 334, no. 1, 132–139, https://doi.org/10.1016/j.jmaa.2006.12.012, MR2332544, ZBL1133.54025.
10.1016/j.jmaa.2006.12.012
Web of Science® Google Scholar
8 Latif A. and Abdou A. A. N., Fixed points of generalized contractive maps, Fixed Point Theory and Applications. (2009) 2009, 9, 487161, MR2486343, ZBL1168.54020.
10.1155/2009/487161
Google Scholar
9 Lim T.-C., A fixed point theorem for weakly inward multivalued contractions, Journal of Mathematical Analysis and Applications. (2000) 247, no. 1, 323–327, https://doi.org/10.1006/jmaa.2000.6866, MR1766943, ZBL0957.47040.
10.1006/jmaa.2000.6866
Web of Science® Google Scholar
10 Ume J. S., Lee B. S., and Cho S. J., Some results on fixed point theorems for multivalued mappings in complete metric spaces, International Journal of Mathematics and Mathematical Sciences. (2002) 30, no. 6, 319–325, https://doi.org/10.1155/S0161171202110350, MR1904672, ZBL1020.47048.
10.1155/S0161171202110350
Google Scholar
11 Blum E. and Oettli W., From optimization and variational inequalities to equilibrium problems, The Mathematics Student. (1994) 63, no. 1–4, 123–145, MR1292380, ZBL0888.49007.
Google Scholar
12 Noor M. A. and Oettli W., On general nonlinear complementarity problems and quasi-equilibria, Le Matematiche. (1994) 49, no. 2, 313–331, MR1397309, ZBL0839.90124.
Google Scholar
13 Ansari Q. H., Al-Homidan S., and Yao J.-C., Equilibrium problems and fixed point theory, Fixed Point Theory and Applications. (2012) 2012, article 25, https://doi.org/10.1186/1687-1812-2012-25, MR2899786.
10.1186/1687-1812-2012-25
Google Scholar
14 Fang Y. P. and Huang N. J., Strong vector variational inequalities in Banach spaces, Applied Mathematics Letters. (2006) 19, no. 4, 362–368, https://doi.org/10.1016/j.aml.2005.06.008, MR2206227, ZBL1138.49300.
10.1016/j.aml.2005.06.008
Web of Science® Google Scholar
15 Giannessi F., Vector Variational Inequalities and Vector Equilibria, 2000, Kluwer Academic Publishers, Dodrecht, The Netherlands, Mathematical Theories, https://doi.org/10.1007/978-1-4613-0299-5, MR1789109.
10.1007/978-1-4613-0299-5
Google Scholar
16 Gong X. H., Strong vector equilibrium problems, Journal of Global Optimization. (2006) 36, no. 3, 339–349, https://doi.org/10.1007/s10898-006-9012-5, MR2263170, ZBL1120.90055.
10.1007/s10898-006-9012-5
Web of Science® Google Scholar
17 Lee G. M., Kim D. S., and Kuk H., Existence of solutions for vector optimization problems, Journal of Mathematical Analysis and Applications. (1998) 220, no. 1, 90–98, https://doi.org/10.1006/jmaa.1997.5821, MR1612075, ZBL0911.90290.
10.1006/jmaa.1997.5821
Web of Science® Google Scholar
18 Long X. J., Huang N. J., and Teo K. L., Existence and stability of solutions for generalized strong vector quasi-equilibrium problem, Mathematical and Computer Modelling. (2008) 47, no. 3-4, 445–451, https://doi.org/10.1016/j.mcm.2007.04.013, MR2378849, ZBL1171.90521.
10.1016/j.mcm.2007.04.013
Google Scholar
19 Plubtieng S. and Sitthithakerngkiet K., Existence result of generalized vector quasiequilibrium problems in locally G-convex spaces, Fixed Point Theory and Applications. (2011) 2011, 13, 967515, MR2780830.
10.1155/2011/967515
Google Scholar
20 Wan A. H., Fu J. Y., and Mao W. H., On generalized vector equilibrium problems, Acta Mathematicae Applicatae Sinica. (2006) 22, no. 1, 21–26, https://doi.org/10.1007/s10255-005-0280-5, MR2191312, ZBL1114.49014.
10.1007/s10255-005-0280-5
Google Scholar
21 Ansari Q. H. and Flores-Bazán F., Generalized vector quasi-equilibrium problems with applications, Journal of Mathematical Analysis and Applications. (2003) 277, no. 1, 246–256, https://doi.org/10.1016/S0022-247X(02)00535-8, MR1954474, ZBL1022.90023.
10.1016/S0022-247X(02)00535-8
Web of Science® Google Scholar
22 Ansari Q. H. and Yao J. C., A. Maugeri and F. Giannessi, On vector quasi-equilibrium problems, Variational Problems and Equilibria, 2003, Kluwer Academic Publishers, Dodrecht, The Netherlands, https://doi.org/10.1007/978-1-4613-0239-1_1, MR2042583, ZBL1069.49003.
10.1007/978-1-4613-0239-1_1
Google Scholar
23 Fu J. Y., Stampacchia generalized vector quasiequilibrium problems and vector saddle points, Journal of Optimization Theory and Applications. (2006) 128, no. 3, 605–619, https://doi.org/10.1007/s10957-006-9034-7, MR2268020, ZBL1103.49010.
10.1007/s10957-006-9034-7
Web of Science® Google Scholar
24 Hou S. H., Yu H., and Chen G. Y., On vector quasi-equilibrium problems with set-valued maps, Journal of Optimization Theory and Applications. (2003) 119, no. 3, 485–498, https://doi.org/10.1023/B:JOTA.0000006686.19635.ad, MR2026460, ZBL1061.90099.
10.1023/B:JOTA.0000006686.19635.ad
Web of Science® Google Scholar
25 Lee G. M., Lee B. S., and Chang S. S., On vector quasivariational inequalities, Journal of Mathematical Analysis and Applications. (1996) 203, no. 3, 626–638, https://doi.org/10.1006/jmaa.1996.0401, MR1417119, ZBL0866.49016.
10.1006/jmaa.1996.0401
Web of Science® Google Scholar
26 Wang S. H., Xiong J. H., and Fu J. Y., Stampacchia generalized vector quasi-equilibriums with monotonicity, Journal of Nanchang University. (2006) 30, 114–117.
Google Scholar
27 Lin L.-J. and Park S., On some generalized quasi-equilibrium problems, Journal of Mathematical Analysis and Applications. (1998) 224, no. 2, 167–181, https://doi.org/10.1006/jmaa.1998.5964, MR1637437, ZBL0924.49008.
10.1006/jmaa.1998.5964
Web of Science® Google Scholar
28 Kazmi K. R. and Khan S. A., Existence of solutions to a generalized system, Journal of Optimization Theory and Applications. (2009) 142, no. 2, 355–361, https://doi.org/10.1007/s10957-009-9530-7, MR2525795, ZBL1178.49009.
10.1007/s10957-009-9530-7
Web of Science® Google Scholar
29 Wu X. and Shen S., A further generalization of Yannelis-Prabhakar′s continuous selection theorem and its applications, Journal of Mathematical Analysis and Applications. (1996) 197, no. 1, 61–74, https://doi.org/10.1006/jmaa.1996.0007, MR1371276, ZBL0852.54019.
10.1006/jmaa.1996.0007
Web of Science® Google Scholar
30 Ding X. P., A coincidence theorem involving contractible spaces, Applied Mathematics Letters. (1997) 10, no. 3, 53–56, https://doi.org/10.1016/S0893-9659(97)00034-7, MR1457639, ZBL0879.54055.
10.1016/S0893-9659(97)00034-7
Web of Science® Google Scholar
31 Balaj M. and Muresan S., Generalizations of the Fan-Browder fixed point theorem and minimax inequalities, Archivum Mathematicum. (2005) 41, no. 4, 399–407, MR2195493, ZBL1111.54032.
Google Scholar

All articles

Existence Solutions of Vector Equilibrium Problems and Fixed Point of Multivalued Mappings

Abstract

1. Introduction

2. Preliminaries

3. Main Theorem

Acknowledgment

References

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Existence Solutions of Vector Equilibrium Problems and Fixed Point of Multivalued Mappings

Abstract

1. Introduction

2. Preliminaries

3. Main Theorem

Acknowledgment

References

Figures

References

Related

Information