Volume 2013, Issue 1 937274

Research Article

Open Access

Model Predictive Control of Piecewise Affine System with Constrained Input and Time Delay

Zhilin Liu,

Zhilin Liu

College of Automation, Harbin Engineering University, Harbin, Heilongjiang 150001, China hrbeu.edu.cn

Search for more papers by this author

Lutao Liu,

Corresponding Author

Lutao Liu

[email protected]

College of Information and Telecommunication, Harbin Engineering University, Harbin, Heilongjiang 150001, China hrbeu.edu.cn

Search for more papers by this author

Jun Zhang,

Jun Zhang

School of Electrical and Information Engineering, Jiangsu University, Zhenjiang, Jiangsu 212013, China ujs.edu.cn

Search for more papers by this author

Xin Yuan,

Xin Yuan

College of Automation, Harbin Engineering University, Harbin, Heilongjiang 150001, China hrbeu.edu.cn

Search for more papers by this author

Zhilin Liu,

Zhilin Liu

College of Automation, Harbin Engineering University, Harbin, Heilongjiang 150001, China hrbeu.edu.cn

Search for more papers by this author

Lutao Liu,

Corresponding Author

Lutao Liu

[email protected]

College of Information and Telecommunication, Harbin Engineering University, Harbin, Heilongjiang 150001, China hrbeu.edu.cn

Search for more papers by this author

Jun Zhang,

Jun Zhang

School of Electrical and Information Engineering, Jiangsu University, Zhenjiang, Jiangsu 212013, China ujs.edu.cn

Search for more papers by this author

Xin Yuan,

Xin Yuan

College of Automation, Harbin Engineering University, Harbin, Heilongjiang 150001, China hrbeu.edu.cn

Search for more papers by this author

First published: 21 December 2013

https://doi.org/10.1155/2013/937274

Citations: 2

Academic Editor: Shen Yin

Share a link

Email
Wechat
Bluesky

Abstract

A model predictive control (MPC) is proposed for the piecewise affine (PWA) systems with constrained input and time delay. The corresponding operating region of the considered systems in state space is described as ellipsoid which can be characterized by a set of vector inequalities. And the constrained control input of the considered systems is solved in terms of linear matrix inequalities (LMIs). An MPC controller is designed that will move the PWA system with time delay from the current operating point to the desired one. Multiple objective functions are used to relax the monotonically decreasing condition of the Lyapunov function when the control algorithm switches from a quasi-infinite horizon to an infinite horizon strategy. The simulation results verify the effectiveness of the proposed method. It is shown that, based on LMI constraints, it is easy to get the MPC for the PWA systems with time delay. Moreover, it is suitable for practical application.

1. Introduction

In engineering practice, there are many hybrid systems described by piecewise affine systems (PWA) which are composed of linear subsystems and convex polytopic regions. Hybrid systems are composed of discrete event dynamic systems and continuous time dynamic systems or discrete time dynamic systems, which interact with each other [1]. The hybrid system theory, which is proposed for the demand of the economic development, is the result of the development of computer science and control theory. Piecewise affine system is one of the most important branches of hybrid system [2]. It consists of some subsystems that integrate the logical and continuous dynamics by switching. Theoretically, any nonlinear system can be approximated as piecewise affine system [3, 4]. In [5], the PWA system is described as ellipsoid which can be characterized by a set of vector inequalities. In [6], the constraint of linear matrix inequalities (LMIs) is released. In terms of LMIs, the PWA system can be stabilized in Lyapunov theory.

Model predictive control (MPC), also known as receding horizon control, is a popular technique for the control of dynamical systems, such as those encountered in chemical process control in the petrochemical, pulp and paper industries, and in industrial hot strip mill [7]. MPC is also a popular technique for the control of dynamical system subject to input and state constraints. At any time instant, MPC requires the online solution of an optimization problem to compute-optimal control inputs over a fixed number of future time instants, known as the finite horizon or quasi-infinite horizon. Using MPC, it is possible to handle inequality constraints on the manipulated and controlled variables in a systematic manner during the design and implementation of the controller [8, 9]. MPC has become the control strategy of choice in industrial applications that typically involve linear systems subject to linear inequality constraints. However, industrial processes are in general inherently nonlinear and operated over a wide range of operating conditions [10, 11]. The use of multiple model/controllers is a common strategy in dealing with the complex of nonlinear systems and has led to the development of various multiple model/controller approaches. Considerable research has been focused on the development and utilization of multiple model/controller banks within the MPC framework [12–14] in order to cope with nonlinear systems. The basis of these approaches is the decomposition of the systems full range of operation into a number of operating regimes in which a simpler local model and/or controller is applied. The local models and controllers are then incorporated to give a global model and/or controller.

Closed-loop stability in multiple model/control approaches has also been studied [15] since designing local controllers that stabilize each individual model may not result in a stable global closed-loop system. In general, the use of piecewise models in a control structure necessitates a means of switching among the available models to the one that best describes the current process dynamics. The switching from one model/controller to another based on a logical argument (supervisory scheme) results in a hybrid system. A closely related work is the stability analysis of piecewise linear systems by [16] in which piecewise quadratic Lyapunov functions were constructed using convex optimization in terms of linear matrix inequalities (LMIs) as an alternative to a globally quadratic Lyapunov function.

Time delay systems are very common in industry. However, few works on control algorithms development for time delay PWA system have been reported [17, 18]. Based on this concept, we propose a MPC control algorithms for the discrete polytopic time-delay PWA systems. The MPC controller of the considered systems is solved in terms of LMIs. The sufficient conditions of stability are derived for time-delay systems. The feedback control law is obtained by convex optimization involving LMIs. The simulation results verify the effectiveness of the proposed method.

Notation. The symbol * will be used in some matrix expressions to induce a symmetric structure. I denotes identity matrix. For example, when H and R are symmetric matrices, then

()

2. Problem Formulation

Consider a discrete time-delay PWA systems with input constraints:

()

where x(k) ∈ Rⁿ is the state of the plant, u(k) ∈ R^m is the control input, and d is fixed time-delay constant. And b_i is constant affine vector of the ith subsystem. i represents the switching rule, which makes value from finite set

, and

. A_i, A_di, B_i, and b_i are sets of known real constant matrices with appropriate dimensions of the ith subsystem separately. The feedback control law is

()

Substituting (3) into inequality (2), we can get

()

where

. Denote X_i as the state region where subsystem i is active at moment k, and there is no switch that occurred at moment k + 1 (see [5]), which is

()

Commonly, X_i is ellipsoid set. The dimension of X_i is less than the dimension of state. To stabilize the PWA system (2), a state feedback control law is solved by defining a quadratic Lyapunov-Krasovskii function:

()

By solving the following two problems, the feedback control law is obtained.

Problem 1. Find a piecewise affine state feedback controller that exponentially stabilizes the PWA system when x(k) ∈ X_i, x(k + 1) ∈ X_i.

Problem 2. It is the same as Problem 1 at the switching moment when x(k) ∈ X_i, x(k + 1) ∈ X_i+1.

Lemma 3. The state region X_i can be described as same ellipsoids X_i⊆ɛ_i, where ɛ_i = {x∣∥E_ix + e_i∥ ≤ 1}. Denote the ellipsoid X_i as the quadratic inequalities (see [5]):

()

More precisely, if

, then the degenerate ellipsoid is described by

()

Finally, it is assumed that the control objective is to stabilize the system to a given point x_cl. With the change of coordinates z = x − x_cl, the problem is transformed to the stabilization of the origin. Accordingly, the ellipsoid changes into

()

where

Assumption 4. In application of this formulation to multiple regions, we assume that we know the order of regions that the states will go through starting from the current region of the system to the terminal region.

Assumption 5. We also assume that we know the number of moves that the system has to take to go from one region to another adjacent operating region.

3. Main Result

Model predictive control, also known as moving horizon control or receding horizon control, has become very successful in process industries, especially in the control of processes that are constrained, multivariable and uncertain. In general, MPC solves online an open-loop optimal control problem subject to system dynamics and constraints at each time instant and implements only the first element of the control profile. At each sampling time k, plant measurements are obtained and a model of the process is used to predict future outputs of the system. Using these predictions, m control moves u(k + m∣k), are computed by minimizing a nominal J_∞(k) over a prediction horizon as follows:

()

where Q_I > 0, R > 0 are symmetric weighting matrices, n is control horizon, x(k + m∣k) is state at time k + m predicted based on the measurements of system (2) at time k. u(k + m∣k) is control move at time k + m computed by solving the optimization problem (10) at time k, u(k + m∣k) is implemented to the system at time k, and then in time k + 1, the maximization problem is solved by deriving an upper bound on the objective function J_∞(k) based on the measurements of new states of system. The control law is obtained by convex optimization based on MPC involving LMIs and ellipsoids constraints (7), which is suitable to practical application.

In this section, the problem formulation for MPC using piecewise linear models of the form (2) is discussed. The aim is to find a sequence of control input signals u(k + n∣k) that will move the system from the current operating point to the desired one. The authors of [19] presented an MPC design technique (min-max MPC) in which the minimization of the nominal objective function was modified to a minimization of the worst case objective function. In this work, we extend this formulation using piecewise affine model with time delay.

Theorem 6. Consider a time-delay PWA system (2) with several operating points, where i denotes the active PWA model and X_i+1 shows the corresponding operating region which if described by |E_i+1x + e_i+1| ≤ 1 with x ∈ X_i+1. u(k∣k) ⋯ u(k + n∣k) are sequences of control inputs to the PWA system. The states of PWA system (2) are steered from X_i to X_(i+1) in n steps, where n is control horizon constant. If there exist Y_i+1 = K_i+1Q, Q ≥ 0, W > 0, γ > 0, ξ > 0, and a sequence of u(k∣k) ⋯ u(k + n∣k) satisfy the following LMI (12)–(16), the sequence of control input signals will move the system from the current operating region to the desired one, until to the origin of the system.

The modified MPC law is given by

()

where x(k + 1∣k) ⋯ x(k + n + 1∣k) are computed iteratively by (2) as follows:

()

and Σ = A_i+1Q + B_i+1Y_i+1,

Proof (1) Upper Bound on the Objective Function. The objective function can be split into two parts:

()

where

()

It is also assumed that the number of moves n required for the system to transition from one part X_i to the next desired part X_(i+1) is prespecified. Using quadratic Lyapunov-Krasovskii function, the upper bound on the objective function

is given as

()

Suppose V(x(k)) satisfies the following inequality:

()

with the conditions V(x(∞∣k)) = 0 and x(∞∣k) = 0. Summing (21) from m = n + 1 to m = ∞ gives

()

Then, the minimization of the upper bound on the objective function

is derived as

()

where P = γQ⁻¹ > 0 and W = γS⁻¹ > 0. Using the S-procedure [6], we get (15).

(2) The Stability of Inequality with Ellipsoids Constraints. In this section, the aim is to design an MPC controller in which the minimization of the nominal objective function was modified to a minimization of the worst case objective function. A thorough discussion of the previous problems can be found in [19]. The objective function of MPC in [19] is

()

where

()

In this section, the objective function min J_∞(k) is replaced by

()

In this section, the MPC formulation given in [19] is extended to PWA system with form (2) that has polytopic and ellipsoid approximations for the operating region X_i. The previous inequalities (27) are the stability constraints for subsystem i + 1. Inequalities (27) can guarantee the PWA system to be steered from X_i to X_i+1 in n steps. The control inputs u(k + mk), m = 0,1 … n are a sequence of free variables, based on the input constraints. If X_i+1 is not the terminal operating ellipsoid region, we apply u(k + m∣k), m = 0 … n to PWA. Once X_i+1 is the terminal operating ellipsoid region, the feedback control law u(k) = K_i+1x(k) is running to reduce the calculation. The quadratic ellipsoid inequality (10) is equivalent to

()

where

Substituting (20) into (21) gives

()

where

()

Using the S-procedure [6] into (28) and (29), we get λ > 0,

()

where

()

By Schur complements, this is equivalent to

()

Substituting P = γQ⁻¹ and pre- and postmultiplying by

gives

()

where

. Pre- and postmultiplying by diag [Q I I I] gives

()

where

()

This is equivalent to

()

Substituting W = γS⁻¹ > 0, ξ = γλ⁻¹, pre- and postmultiplying by

()

we get the inequality (16) by multiple Schur complements.

(3) Input Constraints. It is also possible to incorporate input constraints. We consider bounds on input at time k such as

()

Inputs can be split into sequences:

()

where u(k∣k),u(k + 1∣k) ⋯ u(k + n∣k) are free variables and U_t are future control moves in the terminal region given by the state feedback law.

(1) If PWA does not switches to the terminal operating ellipsoid region, the sequences u(k + m∣k), m = 0 … n are free variables satisfying |u(k + m)| ≤ u_max, m = 0 … n.

(2) If PWA switch to the terminal operating ellipsoid region,

()

where K_i+1 is state feedback matrix, which is equal to LMI (13).

Using the previous techniques, the problem of minimizing an upper bound on the worst-case objective function, subject to input and terminal operating ellipsoid constraints, is reduced to a convex optimization of {u(k∣k), u(k + 1∣k) ⋯ u(k + n∣k), U_t} in terms of LMIs (12)–(16).

Remark 7. Although derived for a time-delay PWA system with ellipsoidal partitions, the optimization problem LMI (16) gives a feasible solution only when , which means the ellipsoidal region X_i does not contain origin [5]. When the ellipsoidal region contains origin, it is assumed that b_i = 0. For convenient notion, we get LMI (16) as follows:

()

Remark 8. If the ellipsoidal region X_i contains origin, it is necessary to substitute (42) into (16) to get a feasible solution.

4. Simulation Result

4.1. Example for Autonomous Land Vehicle

We use the ALV (autonomous land vehicle) model formulated by [20] in this simulation. The objective is to design a controller that forces a cart on the x − y plane to follow the straight line y = 0 with a constant velocity u₀ = 1 m/s (see Figure 1). We assume that a controller has already been designed to maintain a constant forward velocity. The carts path is then controlled by the torque T about z-axis according to the following dynamics:

()

where ψ is the heading angle with time derivative ω, I = 1 kgm² is the moment of inertia of the cart with respect to the center of mass, k = 0.01 Nms is the damping coefficient, and T is the control torque. Due to the limitation of power of the drive motor, the maximum control torque T is roughly 8 Nm. Approximately the control constraint is |T| ≤ T_max = 8. The states of the system are (x₁, x₂, x₃) = (φ, ω, y). We assume that the trajectories can start from any possible initial angle in the range φ₀ ∈ [−3π/5,3π/5] and any initial distance from the line. The function sin(ψ) is approximated by a piecewise affine function yielding a piecewise affine system with 5 regions as follows:

()

To illustrate the proposed results on the time-delay systems, we assume that the system x₂(t) is perturbed by time delay and the delay model is given as

()

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Underactuated surface vessel.

The constant α is the retarded coefficient [21], which satisfies the conditions: α ∈ [0,1]. The limits 1 and 0 correspond to no delay term and to a completed delay term, respectively. In this example, we assume α = 0.7. We construct the following time-delay PWA system:

()

where

, B_1,2,3,4,5 = [0 1 0] ^T,

, b₁ = [0 0 −0.757] ^T, b₂ = [0 0 −0.216] ^T, b₃ = [0 0 0] ^T, b₄ = [0 0 0.216] ^T, b₅ = [0 0 0.757] ^T, u_max = 8.

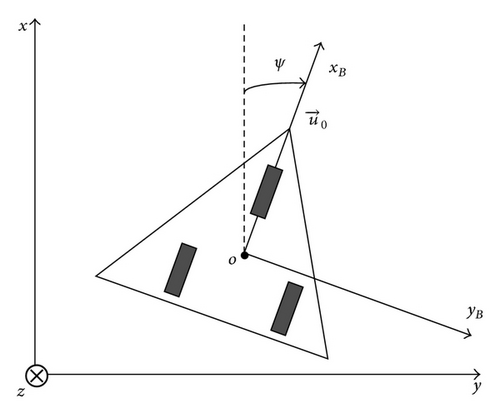
τ = 2 is the time-delay constant. We construct the discrete system by sampling T = 0.02 s, and initial state x(0) = x(−1) = x(−2) = [π/2,0, 3] ^T. By applying Theorem 6, we get the simulation results.

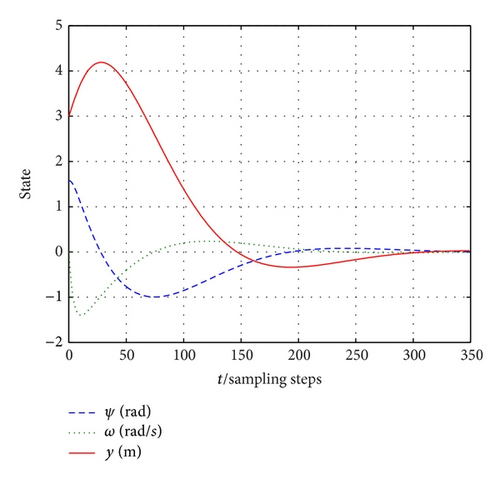
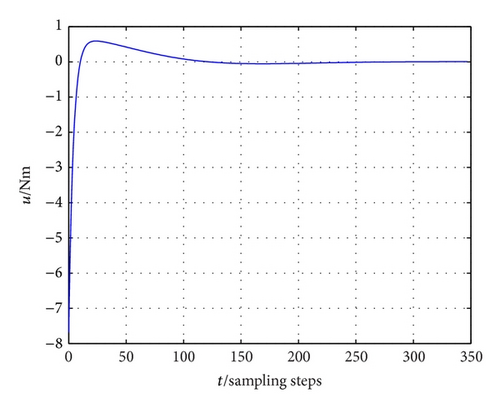
Figures 2 and 3 are the simulation results. Figure 2 shows the state response of the PWA system with time delay. Obviously, all of the states are stable. Figure 3 shows control input action. Physical limitations in ALV impose hard constraints on the torque input. The simulation result in Figure 3 shows that state feedback control strategy can stabilize the PWA system with time-delay subject to input constraints. In this section, the simulation shows the specified constraints on the torque input variable are satisfied.

4.2. Example for Nonlinear Circuit

This example considers a circuit with a nonlinear resistor taken from [5] and shown in Figure 4 with time in 10⁻¹⁰ seconds, the inductor current in mA, and the capacitor voltage in Volts, and the dynamics are

()

Following [5], the characteristic of the nonlinear resistor is described as g(x₂), which is defined to be the piecewise-affine function shown in Figure 5. The corresponding polytopic regions are generated as follows:

()

where L = 100. X_1,2,3 are described as ellipsoids in (10) with the following parameters: E₁ = E₃ = [0,0.01], E₂ = [0,5], e₁ = 1.0044, e₂ = 1.2145, and e₃ = 0.9996.

By using Lemma 3 and the characteristic of the nonlinear resistor, the dynamics (47) is transformed to the PWA system as follows:

()

Respectively, the open-loop equilibrium points of X₁, X₂, and X₃ are

, and

. The objective is to design a piecewise-affine state feedback controller to steer the original state x(0) to close-loop equilibrium

; at the same time the control input constraints |u| ≤ 1(V) must be satisfied.

Using forward differential

, we get the following PWA with time delay, where T = 0.002 s, and initial state is selected as x(0) = x(−1) = x(−2) = [0.5; 0.1] ∈ X₁. To illustrate the proposed results on the time-delay system, we assume that the system x₂(t) is perturbed by time delay and the delay model is given as

()

The constant α is the retarded coefficient [21]. In this example, we assume α = 0.7. τ = 2 is the time-delay constant, where

, B_1,2,3 = [20 0] ^T, b₁ = [0 −0.1422] ^T, b₂ = [0 0.0129] ^T, and b₃ = [0 0] ^T. By applying Theorem 6, we get the following simulation results.

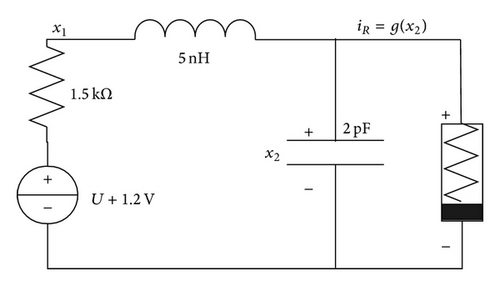
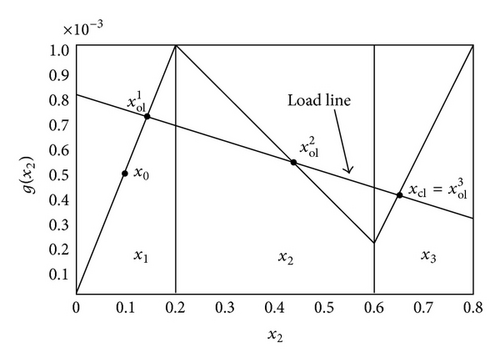
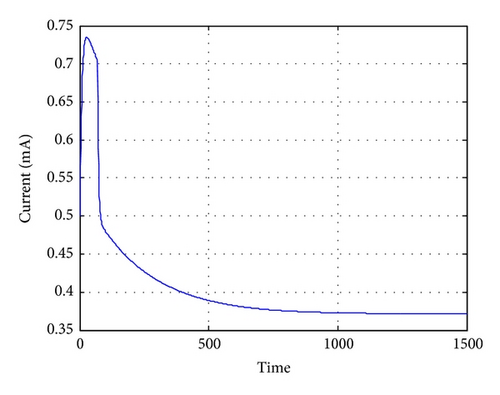
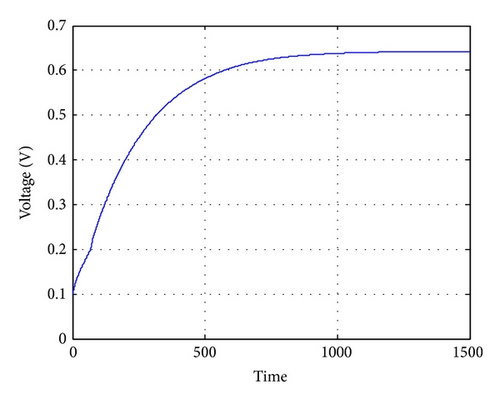
Figures 6 and 7 show the state response of the PWA system with time delay. Trajectory of the current and voltage shows that the original states are steered from X₁ to close-loop equilibrium in X₃. Obviously, all of the states are stable. Figure 8 shows the control input action. The simulation result shows that state feedback control strategy can stabilize the PWA system with time delay subject to ellipsoid constraints. Moreover, the constraint on the control input is satisfied.

5. Conclusion

This work presented a stabilizing multimodel predictive control algorithm which has a contractive constraint to guarantee closed-loop stability. Moreover, the stability of the closed-loop is analyzed by employing the Lyapunov functions approach. Depending on the system state (in the terminal region or outside) the corresponding Lyapunov functions are assigned. The use of multiple objective functions has enabled us to relax the monotonically decreasing condition of the Lyapunov function when the control algorithm switches from a quasi-infinite horizon to an infinite horizon strategy. We have developed a new controller design technique for MPC of piecewise affine systems with time-delay and input constraints. The two simulation examples proposed in Section 4 show that the driving moment (in example 1) and control voltage (in example 2) are limited in amplitude, which makes MPC approach a natural choice for the design of the controller with hard constraints. The technique in this paper leads to convex LMIs based online optimization problem when the local operating regions of the piecewise linear model family are described by ellipsoids. Perhaps the principal shortcoming of MPC proposed is their inability to explicitly incorporate plant model uncertainty. MPC involving data-driven technique is suitable to overcome the previous problem [7, 10, 11, 22, 23]. And it should also be noted that the controller proposed in this paper is developed with known order of regions. In the future work, efforts will be made to design the data-driven MPC controller with uncertain model parameters and switching order.

Acknowledgments

The authors are grateful to the reviewers for their valuable comments. This work is partially supported by National Natural Science Foundation of China (51379044, 61304060, 61201410, and 61104037), Fundamental Research Funds for the Central Universities (HEUCF130804), and Heilongjiang Province Natural Science Foundation Projects (F200916).

References

1 Ferrari-Trecate G., Cuzzola F. A., Mignone D., and Morari M., Analysis of discrete-time piecewise affine and hybrid systems, Automatica. (2002) 38, no. 12, 2139–2146, 2-s2.0-0036888056, https://doi.org/10.1016/S0005-1098(02)00142-5, MR2134879.
10.1016/S0005-1098(02)00142-5
Web of Science® Google Scholar
2 Cuzza F. A. and Morari M., M. D. Di Benedetto and A. S. Vincentelli, A generalized approach for analysis and control of discrete-time piecewise affine and hybrid system, Hybrid System: Computation and Control, 2001, 2034, Springer, Berlin, Germany, 189–203, Lecture Notes in Computer Science, https://doi.org/10.1007/3-540-45351-2_18.
10.1007/3-540-45351-2_18
Google Scholar
3 Kevenaar T. A. M. and Leenaerts D. M. W., Comparison of piecewise-linear model descriptions, IEEE Transactions on Circuits and Systems I. (1992) 39, no. 12, 996–1004, https://doi.org/10.1109/81.207720.
10.1109/81.207720
Web of Science® Google Scholar
4 Johansson M. and Rantzer A., Computation of piecewise quadratic Lyapunov functions for hybrid systems, IEEE Transactions on Automatic Control. (1998) 43, no. 4, 555–559, 2-s2.0-0032045898, https://doi.org/10.1109/9.664157, MR1617547.
10.1109/9.664157
Web of Science® Google Scholar
5 Rodrigues L. and Boyd S., Piecewise-affine state feedback for piecewise-affine slab systems using convex optimization, Systems & Control Letters. (2005) 54, no. 9, 835–853, https://doi.org/10.1016/j.sysconle.2005.01.002, MR2152862.
10.1016/j.sysconle.2005.01.002
Web of Science® Google Scholar
6 Boyd S., El Ghaoui L., Feron E., and Balakrishnan V., Linear Matrix Inequalities in System and Control Theory, 1994, 15, SIAM, Philadelphia, Pa, USA, SIAM Studies in Applied Mathematics, https://doi.org/10.1137/1.9781611970777, MR1284712, MR1284712.
10.1137/1.9781611970777
Google Scholar
7 Ding S., Yin S., Peng K., Hao H., and Shen B., A novel scheme for key performance indicator prediction and diagnosis with application to an industrial hot strip mill, IEEE Transactions on Industrial Informatics. (2012) 9, no. 4, 2239–2247.
10.1109/TII.2012.2214394
Web of Science® Google Scholar
8 Vesely V., Rosinova D., and Quang T. N., Networked output feedback robust predictive controller design, International Journal of Innovative Computing, Information and Control. (2013) 9, no. 10, 3941–3953.
Google Scholar
9 Bououden S., Chadli M., Allouani F., and Filali S., A new approach for fuzzy predictive adaptive controller design using particle swarm optimization algorithm, International Journal of Innovative Computing, Information and Control. (2013) 9, no. 9, 3741–3758.
Google Scholar
10 Yin S., Ding S., and Luo H., Real-time implementation of fault tolerant control system with performance optimization, IEEE Transactions on Industrial Electronics. (2013) 61, no. 5, 2402–2411, https://doi.org/10.1109/TIE.2013.2273477.
10.1109/TIE.2013.2273477
Web of Science® Google Scholar
11 Yin S., Ding S., Haghani A., Hao H., and Zhang P., A comparison study of basic data-driven fault diagnosis and process monitoring methods on the benchmark Tennessee Eastman process, Journal of Process Control. (2012) 22, no. 9, 1567–1581, https://doi.org/10.1016/j.jprocont.2012.06.009.
10.1016/j.jprocont.2012.06.009
CAS Web of Science® Google Scholar
12 Bruno C. and Olivie D., LMI-based multi-model predictive control of an industrial C₃/C₄ splitter, Journal of Control, Automation and Electrical Systems. (2013) 24, no. 4, 420–429, https://doi.org/10.1007/s40313-013-0050-1.
10.1007/s40313-013-0050-1
Google Scholar
13 Dougherty D. and Cooper D., A practical multiple model adaptive strategy for multivariable model predictive control, Control Engineering Practice. (2003) 11, no. 6, 649–664, 2-s2.0-0038537450, https://doi.org/10.1016/S0967-0661(02)00170-3.
10.1016/S0967-0661(02)00170-3
Web of Science® Google Scholar
14 Falugi P., Olaru S., and Dumur D., Multi-model predictive control based on LMI: from the adaptation of the state-space model to the analytic description of the control law, International Journal of Control. (2010) 83, no. 8, 1548–1563, 2-s2.0-77954920584, https://doi.org/10.1080/00207171003736329, MR2729736.
10.1080/00207171003736329
Web of Science® Google Scholar
15 Tian Z. and Hoo K. A., Transition control using a state-shared model approach, Computers and Chemical Engineering. (2003) 27, no. 11, 1641–1656, 2-s2.0-0142107010, https://doi.org/10.1016/S0098-1354(03)00131-5.
10.1016/S0098-1354(03)00131-5
CAS Web of Science® Google Scholar
16 Johansson M. and Rantzer A., Computation of piecewise quadratic Lyapunov functions for hybrid systems, IEEE Transactions on Automatic Control. (1998) 43, no. 4, 555–559, 2-s2.0-0032045898, https://doi.org/10.1109/9.664157, MR1617547.
10.1109/9.664157
Web of Science® Google Scholar
17 Ferrari-Trecate G., Cuzzola F. A., Mignone D., and Morari M., Analysis of discrete-time piecewise affine and hybrid systems, Automatica. (2002) 38, no. 12, 2139–2146, 2-s2.0-0036888056, https://doi.org/10.1016/S0005-1098(02)00142-5, MR2134879.
10.1016/S0005-1098(02)00142-5
Web of Science® Google Scholar
18 Xinping G., Zhiyun L., and Guangren D., Observer-based robust control for uncertain linear systems with time-delay, Control and Decision. (1999) 14, no. 6, 716–720.
Google Scholar
19 Kothare M. V., Balakrishnan V., and Morari M., Robust constrained model predictive control using linear matrix inequalities, Automatica. (1996) 32, no. 10, 1361–1379, 2-s2.0-0030260606, https://doi.org/10.1016/0005-1098(96)00063-5, MR1420038.
10.1016/0005-1098(96)00063-5
Web of Science® Google Scholar
20 Rodrigues L., Dynamic output feedback controller synthesis for piecewise-affine systems [Ph.D. thesis], 2002, Stanford University, Palo Alto, Calif, USA.
Google Scholar
21 Cao Y. and Frank P. M., Stability analysis and synthesis of nonlinear time-delay systems via linear Takagi-Sugeno fuzzy models, Fuzzy Sets and Systems. (2001) 124, no. 2, 213–229, 2-s2.0-0035546633, https://doi.org/10.1016/S0165-0114(00)00120-2, MR1862869.
10.1016/S0165-0114(00)00120-2
Web of Science® Google Scholar
22 Yin S., Ding S., Haghani A., and Hao H., Data-driven monitoring for stochastic systems and its application on batch process, International Journal of Systems Science. (2013) 44, no. 7, 1366–1376, https://doi.org/10.1080/00207721.2012.659708, MR3050076.
10.1080/00207721.2012.659708
Web of Science® Google Scholar
23 Yin S., Yang X., and Karimi H., Data-driven adaptive observer for fault diagnosis, Mathematical Problems in Engineering. (2012) 2012, 21, 832836, https://doi.org/10.1155/2012/832836, MR2992452.
10.1155/2012/832836
Web of Science® Google Scholar

All articles

Model Predictive Control of Piecewise Affine System with Constrained Input and Time Delay

Abstract

1. Introduction

2. Problem Formulation

3. Main Result

4. Simulation Result

4.1. Example for Autonomous Land Vehicle

4.2. Example for Nonlinear Circuit

5. Conclusion

Acknowledgments

References

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Model Predictive Control of Piecewise Affine System with Constrained Input and Time Delay

Abstract

1. Introduction

2. Problem Formulation

3. Main Result

4. Simulation Result

4.1. Example for Autonomous Land Vehicle

4.2. Example for Nonlinear Circuit

5. Conclusion

Acknowledgments

References

Figures

References

Related

Information