Abstract and Applied Analysis
Volume 2013, Issue 1 932085
Research Article
Open Access

The Solution to the BCS Gap Equation for Superconductivity and Its Temperature Dependence

Shuji Watanabe, 

Corresponding Author

Shuji Watanabe

Division of Mathematical Sciences, Graduate School of Engineering, Gunma University, 4-2 Aramaki-machi, Maebashi 371-8510, Japan gunma-u.ac.jp

Search for more papers by this author
First published: 10 September 2013
https://doi.org/10.1155/2013/932085
Citations: 4
Academic Editor: Santanu Saha Ray

Abstract

From the viewpoint of operator theory, we deal with the temperature dependence of the solution to the BCS gap equation for superconductivity. When the potential is a positive constant, the BCS gap equation reduces to the simple gap equation. We first show that there is a unique nonnegative solution to the simple gap equation, that it is continuous and strictly decreasing, and that it is of class C2 with respect to the temperature. We next deal with the case where the potential is not a constant but a function. When the potential is not a constant, we give another proof of the existence and uniqueness of the solution to the BCS gap equation, and show how the solution varies with the temperature. We finally show that the solution to the BCS gap equation is indeed continuous with respect to both the temperature and the energy under a certain condition when the potential is not a constant.

1. Introduction

We use the unit kB = 1, where kB stands for the Boltzmann constant. Let ωD > 0 and k ∈ ℝ3 stand for the Debye frequency and the wave vector of an electron, respectively. Let h > 0 be Planck’s constant, and set ℏ = h/(2π). Let m > 0 and μ > 0 stand for the electron mass and the chemical potential, respectively. We denote by T(≥0) the absolute temperature, and by x the kinetic energy of an electron minus the chemical potential; that is, x = ℏ2 | k|2/(2m) − μ. Note that 0 < ℏωD ≪ μ.

In the BCS model [1, 2] of superconductivity, the solution to the BCS gap equation (1) is called the gap function. The gap function corresponds to the energy gap between the superconducting ground state and the superconducting first excited state. Accordingly, the value of the gap function (the solution) is nonnegative. We regard the gap function as a function of both T and x and denote it by u; that is, u : (T, x) ↦ u(T, x) (≥0). The BCS gap equation is the following nonlinear integral equation (0 < ɛ ≤ x ≤ ℏωD):
()
where U(·, ·) > 0 is the potential multiplied by the density of states per unit energy at the Fermi surface and is a function of x and ξ. In (1) we introduce ɛ > 0, which is small enough and fixed (0 < ɛ ≪ ℏωD). In the original BCS model, the integration interval is [0, ℏωD]; it is not [ɛ, ℏωD]. However, we introduce very small ɛ > 0 for the following mathematical reasons. In order to show the continuity of the solution to the BCS gap equation with respect to the temperature and in order to show that the transition to a superconducting state is a second-order phase transition, we make the form of the BCS gap equation somewhat easier to handle. So we choose the closed interval [ɛ, ℏωD] as the integration interval in (1).

The integral with respect to ξ in (1) is sometimes replaced by the integral over ℝ3 with respect to the wave vector k. Odeh [3] and Billard and Fano [4] established the existence and uniqueness of the positive solution to the BCS gap equation in the case T = 0. For T ≥ 0, Vansevenant [5] determined the transition temperature (the critical temperature) and showed that there is a unique positive solution to the BCS gap equation. Recently, Frank et al. [6] gave a rigorous analysis of the asymptotic behavior of the transition temperature at weak coupling. Hainzl et al. [7] proved that the existence of a positive solution to the BCS gap equation is equivalent to the existence of a negative eigenvalue of a certain linear operator to show the existence of a transition temperature. Moreover, Hainzl and Seiringer [8] derived upper and lower bounds on the transition temperature and the energy gap for the BCS gap equation.

Since the existence and uniqueness of the solution were established for each fixed T in the previous literature, the temperature dependence of the solution is not covered. It is well known that studying the temperature dependence of the solution to the BCS gap equation is very important in condensed matter physics. This is because, by dealing with the thermodynamical potential, this study leads to a mathematical proof of the statement that the transition to a superconducting state is a second-order phase transition. So, in condensed matter physics, it is highly desirable to study the temperature dependence of the solution to the BCS gap equation.

When the potential U(·, ·) in (1) is a positive constant, the BCS gap equation reduces to the simple gap equation (3). In this case, one assumes in the BCS model that there is a unique nonnegative solution to the simple gap equation (3) and that the solution is of class C2 with respect to the temperature T (see e.g., [1] and [9, (11.45), page 392]). In this paper, applying the implicit function theorem, we first show that this assumption of the BCS model indeed holds true; we show that there is a unique nonnegative solution to the simple gap equation (3) and that the solution is of class C2 with respect to the temperature T. We next deal with the case where the potential is not a constant but a function. In order to show how the solution varies with the temperature, we then give another proof of the existence and uniqueness of the solution to the BCS gap equation (1) when the potential is not a constant. More precisely, we show that the solution belongs to the subset VT (see (12)). Note that the subset VT depends on T. We finally show that the solution to the BCS gap equation (1) is indeed continuous with respect to both T and x when T satisfies (20) when the potential is not a constant.

Let
()
where U1 > 0 is a constant. Then the gap function depends on the temperature T only. So we denote the gap function by Δ1 in this case; that is, Δ1 : T ↦ Δ1(T). Then (1) leads to the simple gap equation
()
The following is the definition of the temperature τ1 > 0.

Definition 1 (see [1].)Consider

()

2. The Simple Gap Equation

Set
()

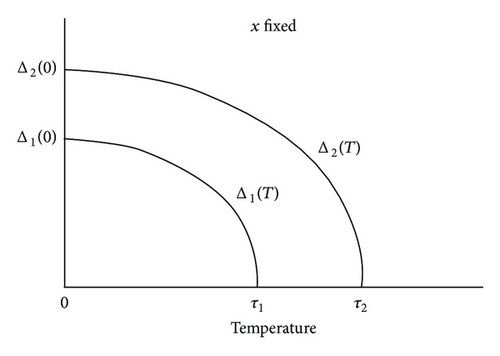
Proposition 2 (see [10], Proposition 2.2.)Let Δ be as in (5). Then there is a unique nonnegative solution Δ1 : [0, τ1]→[0, ∞) to the simple gap equation (3) such that the solution Δ1 is continuous and strictly decreasing on the closed interval [0, τ1]:

()
Moreover, the solution Δ1 is of class C2 on the interval [0, τ1) and satisfies
()

Proof. Setting Y = Δ1(T) 2 turns (3) into

()
Note that the right side is a function of the two variables T and Y. We see that there is a unique function T ↦ Y defined by (8) implicitly, that the function T ↦ Y is continuous and strictly decreasing on [0, τ1], and that Y = 0 at T = τ1. We moreover see that the function T ↦ Y is of class C2 on the closed interval [0, τ1].

Remark 3. We set Δ1(T) = 0 for T > τ1.

Remark 4. In Proposition 2, Δ1(T) is nothing but in [10, Proposition 2.2].

We introduce another positive constant U2 > 0. Let 0 < U1 < U2. We assume the following condition on U(·, ·):
()
When U(x, ξ) = U2 at all (x, ξ)∈[ɛ, ℏωD] 2, an argument similar to that in Proposition 2 gives that there is a unique nonnegative solution Δ2 : [0, τ2]→[0, ∞) to the simple gap equation
()
Here, τ2 > 0 is defined by
()
We again set Δ2(T) = 0 for T > τ2. A straightforward calculation gives the following.

Lemma 5 ([11, Lemma 1.5]). (a) The inequality τ1 < τ2 holds. (b) If  0 ≤ T < τ2, then Δ1(T) < Δ2(T). If T ≥ τ2, then Δ1(T) = Δ2(T) = 0.

Note that Proposition 2 and Lemma 5 point out how Δ1 and Δ2 depend on the temperature and how Δ1 and Δ2 vary with the temperature; see Figure 1.

Details are in the caption following the image
Figure 1
Open in figure viewerPowerPoint
The graphs of the functions Δ1 and Δ2.

Remark 6. On the basis of Proposition 2, the present author [10, Theorem 2.3] proved that the transition to a superconducting state is a second-order phase transition under the restriction (2).

3. The BCS Gap Equation

Let 0 ≤ T ≤ τ2 and fix T, where τ2 is that in (11). We consider the Banach space C[ɛ, ℏωD] consisting of continuous functions of x only and deal with the following subset VT:
()

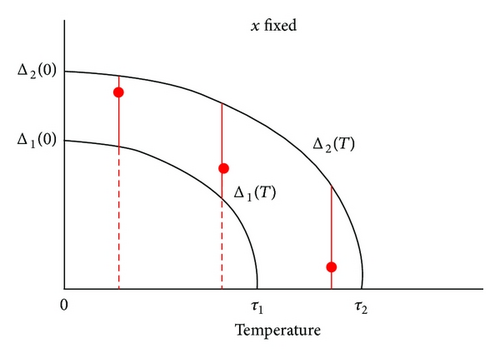
Remark 7. The subset VT depends on T. So we denote each element of VT by u(T, ·); see Figure 1.

As it is mentioned in the introduction, the existence and uniqueness of the solution to the BCS gap equation were established for each fixed T in the previous literature, and the temperature dependence of the solution is not covered. We therefore give another proof of the existence and uniqueness of the solution to the BCS gap equation (1) so as to show how the solution varies with the temperature. More precisely, we show that the solution belongs to VT.

Theorem 8 (see [11], Theorem 2.2.)Assume condition (9) on U(·, ·). Let T ∈ [0, τ2] be fixed. Then there is a unique nonnegative solution u0(T, ·) ∈ VT to the BCS gap equation (1) (x ∈ [ɛ, ℏωD]):

()
Consequently, the solution is continuous with respect to x and varies with the temperature as follows:
()

Proof. We define a nonlinear integral operator A on VT by

()
where u(T, ·) ∈ VT. Clearly, VT is a bounded, closed, and convex subset of the Banach space C[ɛ, ℏωD]. A straightforward calculation gives that the operator A : VT → VT is compact. Therefore, the Schauder fixed point theorem applies, and hence the operator A : VT → VT has at least one fixed point u0(T, ·) ∈ VT. Moreover, we can show the uniqueness of the fixed point; see Figure 2.

Details are in the caption following the image
Figure 2
Open in figure viewerPowerPoint
For each T, the solution u0(T, x) lies between Δ1(T) and Δ2(T).

The existence of the transition temperature Tc is pointed out in the previous papers [5–8]. In our case, it is defined as follows.

Definition 9. Let u0(T, ·) ∈ VT be as in Theorem 8. The transition temperature Tc stemming from the BCS gap equation (1) is defined by

()

Remark 10. Combining Definition 9 with Theorem 8 implies that τ1 ≤ Tc ≤ τ2. For T > Tc, we set u0(T, x) = 0 at all x ∈ [ɛ, ℏωD].

4. Continuity of the Solution with respect to the Temperature

Let U0 > 0 be a constant satisfying U0 < U1 < U2. An argument similar to that in Proposition 2 gives that there is a unique nonnegative solution Δ0 : [0, τ0]→[0, ∞) to the simple gap equation
()
Here, τ0 > 0 is defined by
()
We set Δ0(T) = 0 for T > τ0. A straightforward calculation gives the following.

Lemma 11. (a)  τ0 < τ1 < τ2.

(b) If 0 ≤ T < τ0, then 0 < Δ0(T) < Δ1(T) < Δ2(T).

(c) If τ0 ≤ T < τ1, then 0 = Δ0(T) < Δ1(T) < Δ2(T).

(d) If τ1 ≤ T < τ2, then 0 = Δ0(T) = Δ1(T) < Δ2(T).

(e) If τ2 ≤ T, then 0 = Δ0(T) = Δ1(T) = Δ2(T).

Remark 12. Let the functions Δk  (k = 0, 1, 2) be as above. For each Δk, there is the inverse . Here,

()
and Δ0(0) < Δ1(0) < Δ2(0).

We introduce another temperature. Let T1 satisfy and
()

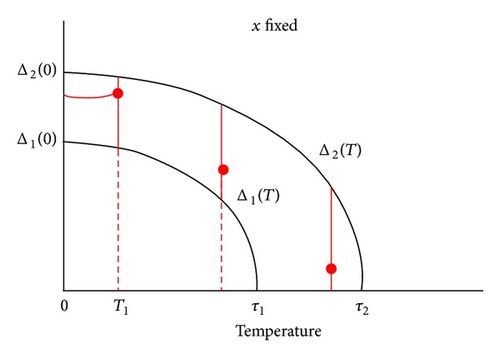
Remark 13. Numerically, the temperature T1 is very small.

Consider the following subset V of the Banach space C([0, T1]×[ɛ, ℏωD]) consisting of continuous functions of both the temperature T and the energy x:
()

Theorem 14 (see [12], Theorem 1.2.)Assume (9). Let u0 be as in Theorem 8 and V as in (21). Then u0 ∈ V. Consequently, the gap function u0 is continuous on [0, T1]×[ɛ, ℏωD].

Proof. We define a nonlinear integral operator B on V by

()
where u ∈ V.

Clearly, V is a closed subset of the Banach space C([0, T1]×[ɛ, ℏωD]). A straightforward calculation gives that the operator B : V → V is contractive as long as (20) holds true. Therefore, the Banach fixed-point theorem applies, and hence the operator B : V → V has a unique fixed point u0 ∈ V. The solution u0 ∈ V to the BCS gap equation is thus continuous both with respect to the temperature and with respect to the energy x; see Figure 3.

Details are in the caption following the image
Figure 3
Open in figure viewerPowerPoint
The solution u0 is continuous on [0, T1]×[ɛ, ℏωD].

Acknowledgment

Shuji Watanabe is supported in part by the JSPS Grant-in-Aid for Scientific Research (C) 24540112.

      The full text of this article hosted at iucr.org is unavailable due to technical difficulties.