Abstract and Applied Analysis
Volume 2013, Issue 1 890126
Research Article
Open Access

Nonexistence Results for the Schrödinger-Poisson Equations with Spherical and Cylindrical Potentials in ℝ3

Yongsheng Jiang, 

Yongsheng Jiang

School of Statistics & Mathematics, Zhongnan University of Economics & Law, Wuhan 430073, China znufe.edu.cn

Search for more papers by this author
Yanli Zhou, 

Yanli Zhou

School of Statistics & Mathematics, Zhongnan University of Economics & Law, Wuhan 430073, China znufe.edu.cn

Department of Mathematics & Statistics, Curtin University, Perth, WA 6845, Australia curtin.edu.au

Search for more papers by this author
B. Wiwatanapataphee, 

Corresponding Author

B. Wiwatanapataphee

Department of Mathematics, Faculty of Science, Mahidol University, Bangkok 10400, Thailand mahidol.ac.th

Search for more papers by this author
Xiangyu Ge, 

Corresponding Author

Xiangyu Ge

School of Statistics & Mathematics, Zhongnan University of Economics & Law, Wuhan 430073, China znufe.edu.cn

Search for more papers by this author
First published: 10 September 2013
https://doi.org/10.1155/2013/890126
Academic Editor: Yonghong Wu

Abstract

We study the following Schrödinger-Poisson system: −Δu + V(x)u + ϕu = |u|p−1u, −Δϕ = u2, lim|x|→+∞ϕ(x) = 0, where u, ϕ : ℝ3 → ℝ are positive radial functions, p ∈ (1, +∞), x = (x1, x2, x3) ∈ ℝ3, and V(x) is allowed to take two different forms including and with α > 0. Two theorems for nonexistence of nontrivial solutions are established, giving two regions on the α − p plane where the system has no nontrivial solutions.

1. Introduction

Schrödinger-Poisson systems arise in quantum mechanics and have been studied by many researchers in the recent years. A number of researches have been focused on quantum transport in semiconductor devices using both mathematical analysis and numerical analysis. Mathematical analysis plays a very crucial role in any investigation. In this paper, we study the nonexistence of nontrivial solutions for the following system in ℝ3:
()
where u, ϕ : ℝ3 → ℝ are positive radial functions, x = (x1, x2, x3) ∈ ℝ3, p ∈ (1, +∞), and V(x) is allowed to have two different forms including and with α > 0.

The above system was introduced in [1] in the study of an N-body quantum problem, that is, the Hartree-Fock system, Kohn-Sham system and, so forth [1–4]. For V(x) in the form of a constant potential, the nonexistence of nontrivial solutions of (1) for p ∉ (1,5) was proved in [5] by using a Pohožaev-type identity. For V(x) in the form of the singular potentials as considered in this work, existence of positive solutions has been established under certain assumption [6]. However, the conditions under which nontrivial solutions do not exist have not yet been full established. Hence, in this paper, we study the nonexistence of solutions to the problem (1) with singular potential.

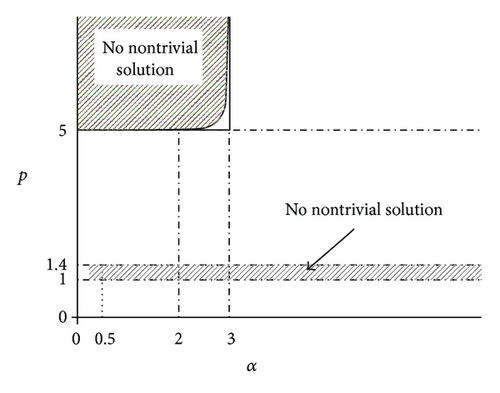
The main contribution of this work is the development of analytical results giving two regions on the α − p plane where the system (1) has no nontrivial solutions. The two α − p regions are shown in Figure 1. The rest of the paper is organized as follows. In Section 2, we first give some basic definitions and concepts and then, based on the method in Badiale et al. [7], establish a Pohožaev-type identity. In Section 3, we give two theorems summarizing the nonexistence results we obtained and then prove the theorems.

Details are in the caption following the image
Figure 1
Open in figure viewerPowerPoint
Diagram showing the two regions on the α − p plane where system (1) has no nontrivial solution.

2. Preliminaries and a Pohožaev-Type Identity

Firstly, we briefly introduce some notation and definitions and recall some properties and known results of the second equations (Poisson equation) in (1). Throughout the paper, we let x = (x1, x2, x3) ∈ ℝ3, D1,2(ℝ3) = {u(x) ∈ L6(ℝ3) : |∇u| ∈ L2(ℝ3)}, , and , and for α > 0 we define
()
By Lemma 2.1 of [2], we know that −Δϕ(x) = u2 has a unique solution in D1,2(ℝ3) with the form of
()
for any u ∈ L12/5(ℝ3), and
()
By the Hardy-Littlewood-Sobolev inequality, we know that is well defined for any u, v ∈ L2∩E. So we can make the following definition.

Definition 1. For i = 1 or 2, if (u, ϕ) ∈ L2∩Lp+1∩Ei∩C2(ℝ3∖{ri = 0}) × D1,2∩C2(ℝ3∖{ri = 0}) satisfies

()
for all v ∈ L2∩Lp+1∩E, we say that (u, ϕ) is a solution of (1).

Now we establish a Pohožaev-type identity based on the work by Badiale et al. [7]. For any u ∈ C2(ℝ3∖{ri = 0}), x ∈ ℝ3∖{ri = 0}, where i = 1, 2, by a simple calculation, we have
()
For any open subset Ω ⊂ ℝ3∖{ri = 0}, by using the divergence theorem and (6), we get
()
So, by multiplying (1) by (x · ∇u) and using (7), we get
()

3. Nonexistence Results for the System of Pohožaev-Type Identity Equations

The nonexistence results we obtained for system (1) are summarized in the following two theorems.

Theorem 2. For x = (x1, x2, x3) ∈ ℝ3 and , if α ∈ (0,3) and p ∈ (1, min {7/5, (3 + α)/(3 − α)})∪[max {5, (3 + α)/(3 − α)}, +∞), or α ∈ [3, ∞) and p ∈ (1,7/5], any solution (u, ϕ) of problem (1) is trivial.

Proof of Theorem 2. Let ∞ > R2 > R1 > 0, BR = {x ∈ ℝ3, |x| < R}, , and ; we then have . Since u ∈ E1∩Lp+1, ϕ ∈ D1,2, we have

()
So, (9) shows that there exist sequences and such that
()
On we have ν(x) = −x/R1,n. By using Cauchy inequality and (10), we get
()
Similarly, we have
()
Hence in (8), by setting , as n → ∞, from (11) and (12), we have
()
By the second equation of (1), we have
()
From (13) and (14), we get
()
On the other hand, multiplying (1) by u and integrating the result over Ω, where Ω ⊂ ℝ3∖{0}, we have
()
Using the divergence theorem to the first term of (16) yields that
()
while the Hölder inequality gives
()
Setting , we have
()
From (16)-(17) and (19), we have
()
By combining (15) and (20), we have
()
For 1 < p ⩽ min {(3 + α)/(3 − α), 7/5} or p⩾max {5, (3 + α)/(3 − α)}, we have
()
Then (21) gives that the solution (u, ϕ) ∈ Lp+1(ℝ3)∩E1(ℝ3)∩C2(ℝ3∖{0}) × D1,2∩C2(ℝ3) must be trivial.

Let . Similar to Theorem 2, we get another nonexistence result to the system (1) with potential function .

Theorem 3. For x = (x1, x2, x3) ∈ ℝ3 and , if α ∈ (0,3) and p ∈ (1, min {7/5, (3 + α)/(3 − α)})∪[max {5, (3 + α)/(3 − α)}, +∞), or α ∈ [3, ∞) and p ∈ (1,7/5], any solution (u, ϕ) of problem (1) with is trivial.

Proof of Theorem 3. For any R2 > R1 > 0, setting , then , where and ν(x) = (−x1/R1, −x2/R1, 0) on . Note that

()
Let
()
Then
()
So we must have such that
()
By using Cauchy inequality and (24)–(26), we have
()
It is easy to see that and . Let in (18) by using the definition of and (27), we get
()
Similar to (12), we have such that
()
As n → +∞, (28)–(29) imply that
()
Since , we have
()
On the other hand, we have
()
So if we multiply (1) by u and then integrate over the domain and let n → +∞, we have
()
As for (20), we have
()
From (31) and (34), we have
()
For 1 < p ⩽ min {(3 + α)/(3 − α), 7/5} or p⩾max {5, (3 + α)/(3 − α)}, (35) implies that the solution of problem (1) with i = 2, (u, ϕ) ∈ Lp+1(ℝ3)∩E2(ℝ3)∩C2(ℝ3∖{0}) × D1,2∩C2(ℝ3), which satisfies , must be trivial.

4. Conclusion

We mainly study the nonexistence of nontrivial solutions to system (1) in this paper, giving two regions on the α − p plane where the system (1) has no nontrivial solutions; see Figure 1. In another paper, we will study the existence of nontrivial solutions to system (1).

Acknowledgments

This research was supported by the National Science Foundation of China (NSFC)(11201486), the Chinese National Social Science Foundation (10BJY104) and the Fundamental Research Funds for Central Universities (31541311208). B. Wiwatanapataphee gratefully acknowledges the support of the Faculty of Science, Mahidol University.

      The full text of this article hosted at iucr.org is unavailable due to technical difficulties.