On the Stability of a Compressible Axial Flow with an Axial Magnetic Field
Abstract
We consider the stability problem of inviscid compressible axial flows with axial magnetic fields following the work of Dandapat and Gupta (Quarterly of Applied Mathematics, 1975). A numerical study of the stability of some basic flows has been carried out and it is found that an increase in the magnetic field strength has a stabilizing effect on subsonic flows and a destabilizing effect on supersonic flows. An analytical study of the stability problem has also been done in the present paper, but this analytical study is restricted by the approximation M ≪ 1 and ci ≪ 1, where M is the Mach number and ci is the imaginary part of the complex phase velocity c. A semicircular region depending on the magnetic field parameter and the Mach number is found for subsonic disturbances and as a consequence it is found that sufficiently strong magnetic field stabilizes all subsonic disturbances. Under a weak magnetic field, it is shown that short subsonic disturbances are stable.
1. Introduction
The stability of inviscid shear flows of a compressible fluid was studied in Blumen [1]. In order to simplify the stability problem, Blumen [1] focused attention on the stability of basic parallel shear flow of a perfect gas whose thermodynamic state is constant. From the equations of motion, the pressure of the shear flow is a constant only and if the basic flow temperature is also a constant, it follows that the basic flow density is also a constant. In the context of magnetogasdynamics, Dandapat and Gupta [2] studied the stability of a parallel flow of an inviscid perfectly conducting gas in the presence of a uniform magnetic field. Following Blumen [1], Dandapat and Gupta [2] also considered the case of a constant basic thermodynamic state. In Dandapat and Gupta [3] the stability of a nondissipative axial flow of a compressible conducting fluid between two concentric cylinders in the presence of a uniform axial field was studied. In cylindrical polar coordinates (r, θ, z) they considered the basic flow with velocity (0,0, W(r)), magnetic field (0,0, H0), where H0 is a constant, P0(r) is the pressure, and ρ0(r) is the density. In the absence of the swirl component of the velocity in the basic flow it follows from the equations of magnetohydrodynamics that P0 is a constant. In their stability analysis, Dandapat and Gupta [3] noticed that the equation involving the density perturbation ρ0 is not needed in deriving the stability equation. Dandapat and Gupta [3] explained this by observing that there is no basic swirl velocity and therefore the mechanism of the centrifugal acceleration playing the role of a radial effective gravity is absent in this stability analysis. Consequently we consider the stability of a basic flow of a compressible fluid, whose thermodynamic state is constant.
The instability of an incompressible MHD basic flow with an axial velocity profile with a constant shear has been studied numerically in Shumlak and Roderick [4]. Four simulations were performed with varying values of peak velocity. Since Shumlak and Roderick [4] have considered basic flows with linear basic velocity profiles and variable density basic profiles, their numerical results show that increasing the value of the peak velocity reduces the Rayleigh-Taylor instability due to density variations. It may be noted here that Shumlak and Roderick [4] have also done an analytical study of the stability problem but in slab geometry and not in cylindrical geometry as in the case with their numerical study. However it has been observed in Zhang and Ding [5] that the incompressibility condition makes the effects of the plasma compressibility and magnetic field undetectable. But in the early stage of implosion, due to the relatively low plasma temperature, the effect of the compressibility becomes important. Consequently, the impact of compressibility on the stability in Z-pinch implosions in which equilibrium axial flows are included has been studied in Zhang and Ding [5]. However Zhang and Ding [5] have considered only the slab geometry and not cylindrical annular geometry. The basic axial velocity profile is a linear profile as in Shumlak and Roderick [4]. It is found from the study of Zhang and Ding [5] that the effect of plasma compressibility is to reduce the growth rate of unstable modes. It is observed in Zhang and Ding [5] that the incompressible approximation neglects the effects of compressibility and magnetic field, which will become important when the plasma temperature is relatively low. Therefore in the early stage of implosion, the compressibility model is much more suitable than the incompressible one. With the cooperation of sheared axial flow and magnetic field, it is found that plasma compressibility improves the stability of the basic flow significantly.
In their work, Dandapat and Gupta [3] have discussed the axisymmetric stability of a pure axial flow with velocity (0,0, W(r)) of a compressible perfectly conducting fluid between two concentric cylinders permeated by a uniform axial magnetic field. They have shown that the complex wave speed c ( = cr + ici, ci > 0) for any unstable wave lies in a semicircle in the upper half plane, having the range of the axial velocity as the diameter. In the incompressible case the same problem has been studied earlier in Howard and Gupta [6] and it is shown that the instability region is given by a semicircle of radius , where a = min W(r), b = max W(r), and VA is the Alfven velocity. It is seen that the instability region depends on the magnetic field and one can conclude from this that a sufficient condition for stability to axisymmetric perturbations of axial flow of an incompressible fluid with uniform axial magnetic field is that the Alfven speed of the axial field should exceed half the maximum velocity difference.
A natural question that arises here is whether we can get a semicircle theorem for compressible flows where the radius depends on the magnetic field and consequently we can get a sufficient condition for stability as the magnetic field to be sufficiently strong. In this paper we find an answer to this question by obtaining such a semicircle for a special class of basic flows and for a special class of disturbances. We consider a basic flow with velocity field (0,0, W(r)) and we denote the Mach number by M. The special class of basic flows considered in the analysis satisfies the conditions M ≪ 1 and ci ≪ 1 so that their product can be ignored in comparison to unity. The special class of disturbances considered in the analysis is the subsonic ones which satisfy the condition 1 − M2(W − cr) 2 > 0. Since a sufficiently strong magnetic field stabilizes the axial flow we study the problem under the weak magnetic field approximation and show that short waves are stable.
Then we make a numerical study of the same problem for a family of symmetric velocity profiles but without making any approximations and without any restrictions on the disturbances. The growth rate αci versus the wave number α and the neutral curves in the α − M plane are plotted for various values of the Mach number M and the magnetic field parameter S. It is found that an increase in the magnetic field strength has a stabilizing effect on subsonic flows and a destabilizing effect on supersonic flows. Furthermore it is found that all unstable modes are Holmboe modes, that is, propagating modes, and that they are long wave modes.
2. Formulation of the Problem
Consider nondissipative axial flow of a compressible conducting fluid between two concentric cylinders at r = R1, R2 in the presence of a uniform axial magnetic field. Thus, in cylindrical coordinates (r, θ, z) the basic velocity and magnetic fields are given by (0,0, W(r)) and (0,0, H0), respectively, and the pressure and density are constants P0 and ρ0, respectively.
Here M = V/a0 is the Mach number which is a measure of the compressibility of the fluid and is the magnetic field parameter which is a measure of the strength of the basic magnetic field. We have chosen to denote the magnetic field parameter by S following the works of S. C. Agrawal and G. S. Agrawal [7] and Rathy and Kishan [8]. Here D = d/dr and D* = D + 1/r.
3. Analytical Results
The disturbances are classified (under Shivamoggi’s approximation) as subsonic, sonic, or supersonic according to 1 − M2(W − cr) 2 > , = , <0. Sonic disturbances satisfy the condition 1 − M2(W − cr) 2 = 0 and their existence is possible only when W is a constant. From the semicircle theorem of Dandapat and Gupta [3] it follows that such a basic flow is stable and the neutral modes move with speed cr = W ± 1/M. For subsonic modes the wave velocity cr of any disturbance satisfies the inequalities Wmin − 1/M < cr < Wmax + 1/M and this means that the wave velocity of subsonic modes is bounded. For supersonic modes the wave velocity cr satisfies the inequalities cr ≤ Wmin − 1/M or cr ≥ Wmax + 1/M and this means that the wave velocity of supersonic modes needs not to be bounded. Thus the classification of the disturbances is based on the speed of propagation of the disturbances. Here it may be recalled that the basic flow (i) is a subsonic flow if M < 1, (ii) a sonic flow if M = 1, and (iii) a supersonic flow if M > 1. Hence our classification of the disturbances as subsonic, sonic, and supersonic is different from the classification of the basic flows.
For an incompressible flow M = 0, this reduces to the semicircle theorem of Howard and Gupta [6].
Thus we see that a sufficiently strong axial magnetic field stabilizes an axial flow (under the restrictions mentioned earlier). This result reduces to the sufficient conditions of Howard and Gupta [6] for incompressible flows.
For an unstable mode ci > 0 and the transformation G = (W−c)1/2F is well defined.
4. Numerical Results
Here the value of the parameter λ3 does not affect the stability of the flow, but we choose a suitable value of λ3 for making W(r) zero on the boundaries.
In Figure 1 we have plotted a family of velocity profiles corresponding to different values of λ1 in (21) and a fixed value of λ2. All velocity profiles are symmetric profiles about r = (R1 + R2)/2. An increase in λ1 corresponds to an increase in (Wmax − Wmin ).
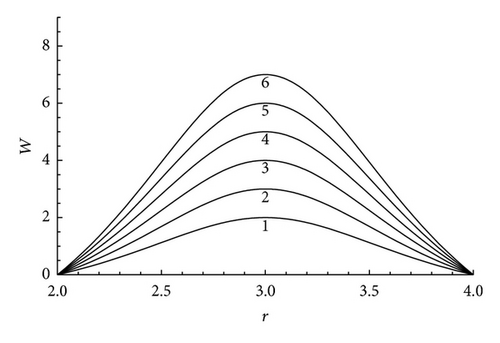
From Figure 2 it is seen that that an increase in λ1 corresponds to an increase in the range of unstable wave numbers and consequently we can conclude that an increase in the value of (Wmax − Wmin ) corresponds to an increase in instability. However we should observe from Figure 2 that the maximum growth rate of unstable modes does not always increase with an increase in the values of λ1. It is seen that the maximum growth rate increases with an increase in λ1 up to a certain value of λ1 and when λ1 increase beyond that value the maximum growth rate is found to be decreasing. Hence the conclusion we can make from Figure 2 is that the enhancement of instability due to an increase in λ1 is by the increase in the spectral range of instability and not by an increase in the maximum growth rate of unstable modes.
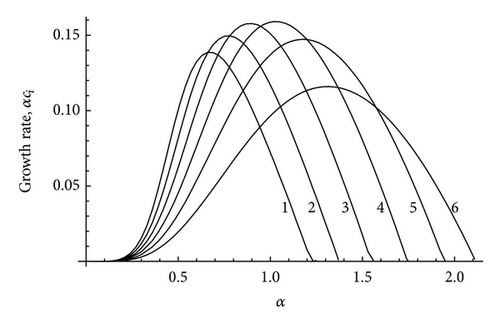
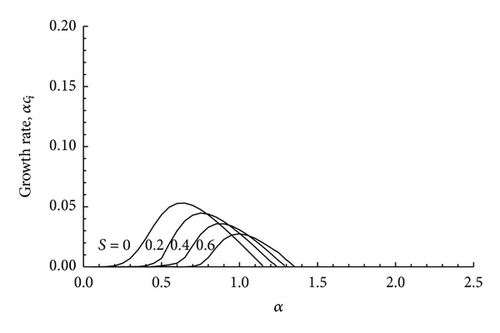
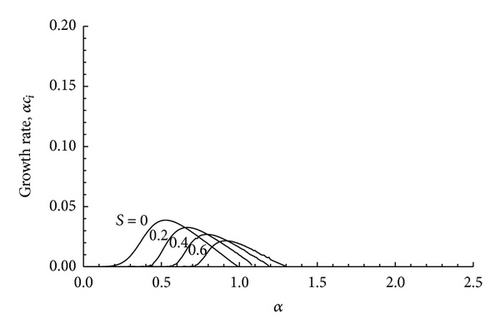
In Figure 3 we have plotted some velocity profiles corresponding to different values of λ1 and λ2. All these velocity profiles have the same value at the end points and the same value of Wmax . From Figure 4 it is seen that when S = 0 and M = 0.5, the spectral range is small for the outer profile and the spectral range is increased for the inner profiles. This may be because increases as we move from the outer profile to the inner profile. It is also seen that the growth rate curves for S = 0, M = 0.5 case are always below the growth rate curves for the purely hydrodynamic case of S = 0 and M = 0. Thus compressibility is seen to have a stabilizing effect on all the velocity profiles.

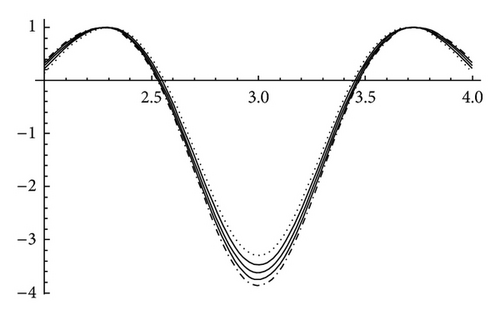
In Figure 5 we have plotted the classifier expression 1 − M2(W − cr) 2 between the radial region from r = 2 to 4 for the eigenvalue cr obtained in each case for the axial velocity profile number 2. Mach number M is taken as 1.0 and magnetic field strength parameter S is increased from 0 through 0.2, 0.4, 0.6, and 0.8 and the corresponding five plots are shown above. Here we observe that the disturbance mode satisfies the condition of being subsonic, sonic, and supersonic modes. The supersonic condition is satisfied in the central region of the flow profile. The dot-dashed curve corresponds to S = 0.8 and the dotted one corresponds to S = 0. From the above plots we can infer that an increase in axial magnetic field strength enhances the speed of supersonic disturbances slightly. The axial velocity profile and other parameters used here are the same which we have used in Figure 5. There we have seen that, beyond the magnetic field strength of 0.9, the flow becomes stabilized. In the above figure, the value of (b−a)2/4(1 − M2(b − a) 2) is −0.333333 for all the five curves and is less than S in each case. The sufficient condition for stabilization of subsonic flows with strong magnetic field, which we have obtained in the analytical Section 3, that is S ≥ (b−a)2/4(1 − M2(b − a) 2), the subsonic disturbances are stabilized as per the above condition and since the flow is still unstable as seen from the growth rate plots of Figure 9, it is the supersonic disturbances that cause the flow instability. But further increase in the value of S (beyond 0.9) ensures complete stability. So we may infer from the above discussions that the subsonic disturbances get stabilized earlier than the supersonic disturbances as we increase the magnetic field strength parameter S. In other words, the magnetic field strength required for stabilization of supersonic disturbances has to be more than that needed for the stabilization of subsonic disturbances.
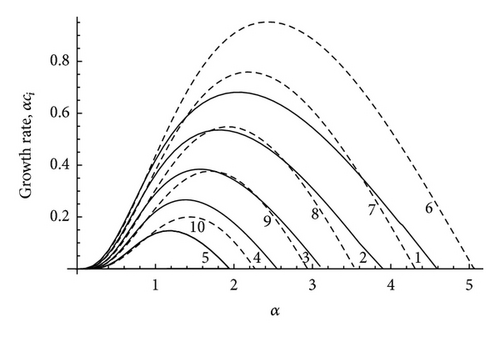
In Figures 6, 7, 8, 9, 10, and 11 we have plotted the growth rate αci versus the wave number α for various values of S and by choosing particular value for the Mach number M. We have considered three subsonic basic flows with M = 0.25, M = 0.5, and M = 0.75, a sonic basic flow for which M = 1, and two supersonic basic flows with M = 1.25 and M = 1.5. It is seen that the spectral range (the range of α for which the instability occurs) in the magnetic case (i.e., S ≠ 0) lies within the spectral range for the nonmagnetic range (S = 0) only for the subsonic flows, while the spectral range gets shifted to the right for the sonic and supersonic flows with an increase in the magnetic field parameter S. This means that the stabilizing role of compressibility is reduced by an increase in the magnetic field strength. This is also seen from the neutral curves.
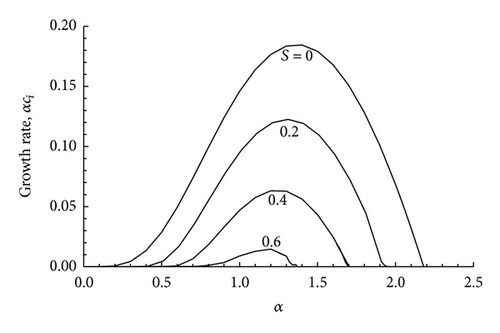
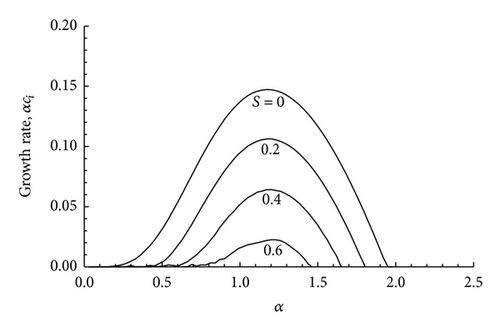
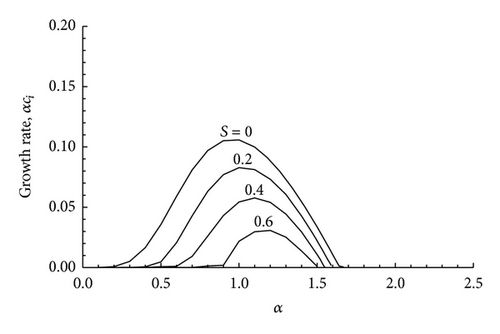
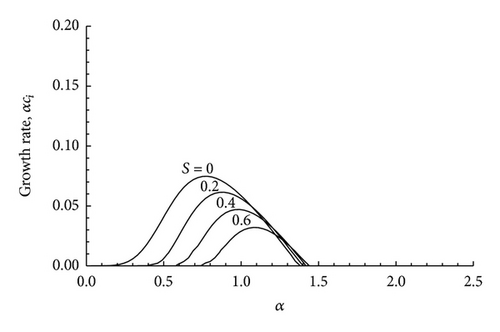
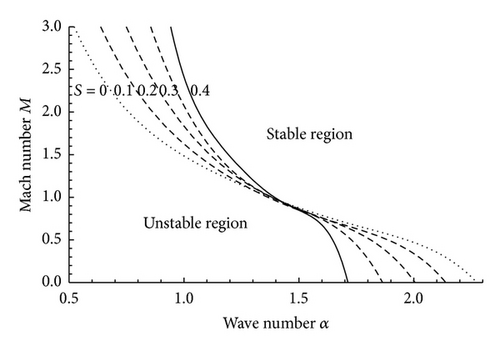
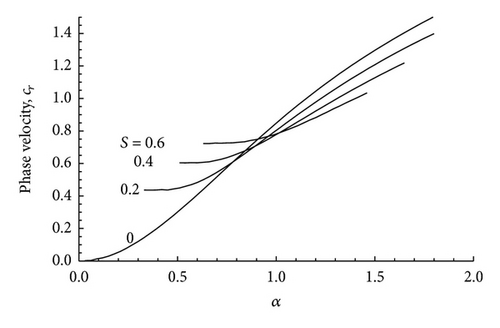
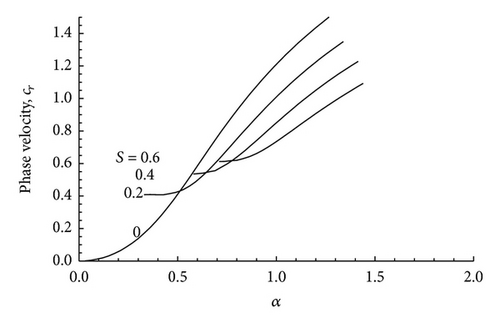
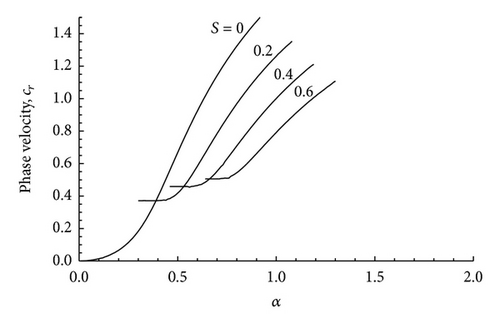
In Figure 12 we have plotted the neutral curves, that is, curves in which ci = 0, in the α − M plane for various values of S. All these neutral curves intersect at a particular point. In comparison to the neutral curve for S = 0 (i.e., the nonmagnetic case) the other neutral curves lie below the S = 0 curve in the right side of the intersection point, while the neutral curves for S ≠ 0 lie above the neutral curves for S = 0 to the left of the intersection point. It is seen from Figure 12 that the magnetic field has a stabilizing effect on the subsonic flows (M < 1) and a destabilizing effect on supersonic ones (M > 1). In Figures 13, 14, and 15 we have plotted the phase velocity cr versus the wave number for different values of the Mach number M. In all the cases it is found that cr ≠ 0. This means that the unstable modes are Holmboe mode (i.e., propagating modes).
5. Discussion and Concluding Remarks
Dandapat and Gupta [2] have discussed the physical interpretation of the stabilizing effect of the compressibility of the fluid and that of the magnetic field. Compressibility is stabilizing because certain amount of the basic flow energy must be used to do work against the force due to the elasticity of the medium before it becomes available to cause instability, while the stabilizing effect of the magnetic field is due to the restoring force offered by the tension along the magnetic lines. In the context of the stability of axial flows of a compressible fluid in the presence of an uniform axial magnetic field, Dandapat and Gupta [3] have obtained a semicircle theorem for the axisymmetric unstable modes. In the present paper we have considered this problem under the approximation M ≪ 1 and ci ≪ 1 (cf. Shivamoggi [9]) and have found an improved instability region which includes the magnetic field parameter S and the compressibility parameter M in the radius of the semicircle. The stabilizing effect of a strong magnetic field follows from this result. Consequently we have studied the problem under the weak magnetic field approximation and we have found that short waves are stable. From this it follows that a weak magnetic field is also stabilizing the disturbances.
Because of the complexity of the mathematical problem, analytical study of the stability of axial flows of a compressible fluid in the presence of a uniform magnetic field is limited. Consequently we have made a numerical study of this stability problem in the present work. Here it may be emphasized that in the numerical study of the problem, the approximation made in the analytical study presented in Section 3 of the present paper is not made and also that the disturbances are not restricted to be of any particular type. We have chosen a family of symmetric velocity profiles and the numerical study of their stability consists of finding the growth rate of the unstable modes and also their propagation speed. The growth rate αci versus the wave number α and the neutral curves in the α − M plane are plotted for various values of the Mach number M and the magnetic field parameter S. It is found that an increase in the magnetic field strength has a stabilizing effect on subsonic flows and a destabilizing effect on supersonic flows. Another conclusion of our numerical study is that the unstable disturbances are all Holmboe modes, that is, propagating modes, and that they are all long wave modes.
| Profile number | λ1 | λ2 | λ3 |
|---|---|---|---|
| 1 | 3.0183 | 3.50 | 0.33736 |
| 2 | 4.5274 | 3.50 | 0.33736 |
| 3 | 6.0365 | 3.50 | 0.33736 |
| 4 | 7.5456 | 3.50 | 0.33736 |
| 5 | 9.0547 | 3.50 | 0.33736 |
| 6 | 10.5638 | 3.50 | 0.33736 |
| 7 | 3.193 | 7.00 | 0.0603 |
| 8 | 3.331 | 6.00 | 0.0993 |
| 9 | 3.584 | 5.00 | 0.1631 |
| 10 | 3.924 | 4.25 | 0.2355 |
| 11 | 4.528 | 3.50 | 0.3374 |
Acknowledgments
The authors are thankful to the referee for his constructive comments that helped them to improve their paper. The second author is grateful to Professor B. Veenadhari, Area Chairperson, Observatory and Data Analysis Division, and the Director, Indian Institute of Geomagnetism, Panvel, Mumbai, India for giving encouragement to do this research work.




