Volume 2013, Issue 1 868035

Research Article

Open Access

A Finite Element Method for the Multiterm Time-Space Riesz Fractional Advection-Diffusion Equations in Finite Domain

Jingjun Zhao,

Jingjun Zhao

Department of Mathematics, Harbin Institute of Technology, Harbin, Heilongjiang 150001, China hit.edu.cn

Search for more papers by this author

Jingyu Xiao,

Jingyu Xiao

Department of Mathematics, Harbin Institute of Technology, Harbin, Heilongjiang 150001, China hit.edu.cn

Search for more papers by this author

Yang Xu,

Corresponding Author

Yang Xu

[email protected]

orcid.org/0000-0001-6543-5935

Department of Mathematics, Harbin Institute of Technology, Harbin, Heilongjiang 150001, China hit.edu.cn

Search for more papers by this author

Jingjun Zhao,

Jingjun Zhao

Department of Mathematics, Harbin Institute of Technology, Harbin, Heilongjiang 150001, China hit.edu.cn

Search for more papers by this author

Jingyu Xiao,

Jingyu Xiao

Department of Mathematics, Harbin Institute of Technology, Harbin, Heilongjiang 150001, China hit.edu.cn

Search for more papers by this author

Yang Xu,

Corresponding Author

Yang Xu

[email protected]

orcid.org/0000-0001-6543-5935

Department of Mathematics, Harbin Institute of Technology, Harbin, Heilongjiang 150001, China hit.edu.cn

Search for more papers by this author

First published: 15 April 2013

https://doi.org/10.1155/2013/868035

Citations: 7

Academic Editor: Xinan Hao

Share a link

Email
Wechat
Bluesky

Abstract

We present an effective finite element method (FEM) for the multiterm time-space Riesz fractional advection-diffusion equations (MT-TS-RFADEs). We obtain the weak formulation of MT-TS-RFADEs and prove the existence and uniqueness of weak solution by the Lax-Milgram theorem. For multiterm time discretization, we use the Diethelm fractional backward finite difference method based on quadrature. For spatial discretization, we show the details of an FEM for such MT-TS-RFADEs. Then, stability and convergence of such numerical method are proved, and some numerical examples are given to match well with the main conclusions.

1. Introduction

Fractional differential equations are different from integer ones, in which the nature of the fractional derivative introduces the memory effect, thus increasing its modeling ability. Recently, many mathematical models with fractional derivatives have been successfully applied in biology, physics, chemistry, and biochemistry, hydrology, and finance [1–3]. The multiterm fractional differential equations have been widely studied in rheology, and, in many cases, the exact solutions are known [4, 5]. Summary of the fractional differential equations can be found in monographs [6–9]. As one of the main branch, fractional partial differential equations have attracted great attention. Therefore, the numerical treatment and supporting analysis of fractional order partial differential equations have become an important research topic that offers great potential.

The FEM is one of the effective numerical methods for solving traditional partial differential equations. For fractional partial differential equations, FEM also can be a useful and effective numerical method. In recent years, some valuable papers are concerned with the FEM for fractional differential equations. Adolfsson et al. [10, 11] considered an efficient numerical method to integrate the constitutive response of fractional order, viscoelasticity based on the FEM. Roop and Ervin [12–15] investigated the theoretical framework for the Galerkin finite element approximation to some kinds of fractional partial differential equations. Li et al. [16] considered numerical approximation of fractional differential equations with subdiffusion and superdiffusion by using difference method and finite element method. Li and Xu [17, 18] proposed a time-space spectral method for time and time-space fractional partial differential equation based on a weak formulation, and a detailed error analysis was carried out. Jiang and Ma [19] considered a high-order FEM for time fractional partial differential equations and proved the optimal order error estimates. Ford et al. [20] studied an FEM for time fractional partial differential equations.

Fractional advection-diffusion equations especially are important in describing and understanding the dispersion phenomena. Analytical solutions of such equations in finite domain have been obtained by Park in [21]. Also, the Riesz fractional advection-diffusion equations (RFADEs) with a symmetric fractional derivative (the Riesz fractional derivative) were derived from the kinetics of chaotic dynamics by [22] and summarized by [23]. Ciesielski and Leszczynski [24] presented a numerical solution for such equations based on the finite difference method.

One often sees RFADEs defined in terms of the fractional Laplacian as follows:

()

for example, where u is a solute concentration, k_α and k_β represent the dispersion coefficient and the average fluid velocity. Here, the fractional Laplacian operator −(−Δ) ^α/2 uses the Fourier transformation on an infinite domain, with a natural extension to include finite domains when the function u(t, x) is subject to the zero Dirichlet boundary conditions (see [9]). Due to Lemma 1 in [25], the fractional Laplacian operator −(−Δ) ^α/2 on an infinite domain x ∈ (−∞, ∞) is equivalent to the Riesz fractional derivative operator

. In particular, the Riesz fractional derivatives include both the left and the right Riemann-Liouville derivatives that allow the modeling of flow regime impacts from either side of the domain. Yang et al. [25] investigated the numerical treatment for the RFADE with the Riesz space fractional derivative as

()

where

is the Riesz space fractional operator defined in Section 2.

To increase the modeling ability, some authors considered the equations with the fractional order in both time and spatial variables in RFADEs, which include more information and hence are more interesting. For the time-space fractional advection-dispersion equations, Shen et al. [26] presented the fundamental solution and numerical solution of the Riesz fractional advection-dispersion equation with initial and boundary conditions on a bounded domain, and derived the stability and convergence of their proposed numerical methods. Then, for fractional advection-diffusion equations, Shen et al. [27] presented an explicit difference approximation and an implicit difference approximation for the time-space Riesz-Caputo fractional advection-diffusion equations with initial and boundary conditions on a finite domain.

All of the above papers only considered single-term fractional equations in time variable, where only one fractional differential operator appeared. In this paper, we consider the multiterm fractional differential equation, which includes more than one fractional derivative. For example, the so-called Bagley-Torvik equation [28] is

()

where A, B, and C are certain constants and f is a given function. The Basset equation is, in [6],

()

where 0 < α < 1, b, and c are positive real numbers. This equation describes the forces that occur when a spherical object sinks in an incompressible viscous fluid.

Recently, some authors considered the applications of multiterm fractional differential equations [29] and the numerical methods for such equations [30–32]. At the same time, the multiterm fractional partial differential equations have been proposed in [33, 34]. The analytical solution and the numerical methods for multiterm time fractional wave-diffusion equations have been investigated in [35, 36]. This motivates us to consider the effective numerical solution for such multiterm fractional partial differential equations.

In this paper, we consider MT-TS-RFADEs in finite domain with the zero Dirichlet boundary conditions. The analytical solution of such MT-TS-RFADEs has been investigated by Jiang et al. in [37]. Here, we present an FEM for a simplified MT-TS-RFADEs and obtain the optimal order error estimates both in semidiscrete and fully discrete cases and derive the stability of such FEM. As far as we are aware, there are few research papers in the published literature written on this topic.

This paper is organized as follows. In Section 2, the preliminaries of the fractional calculation are shown. Then, we give the weak formulation of MT-TS-RFADEs and prove the existence and uniqueness of this problems by the well-known Lax-Milgram theorem. In Section 3, we present the convergence rate of Diethelm’s fractional backward difference method (see [38, 39]) for time discretization. In Section 4, we propose a finite element method based on the weak formulations and carry out the error analysis. In Section 5, we prove the stability of such FEM for MT-TS-RFADEs. Finally, some numerical examples are considered in Section 6.

2. Existence and Uniqueness

We consider the MT-TS-RFADEs with multiterm time fractional derivatives and the Riesz space fractional derivatives in the following form:

()

where 0 < β < 1, 1 < γ < 2, x ∈ [0, X], and t ∈ [0, T] are respectively the space and time variables and k_β, k_γ are positive constants. We consider this problem with the zero Dirichlet boundary value conditions and the initial value condition defined as follows:

()

For nonzero boundary value conditions, we need to transform the problem into one with zero boundary value conditions before using the method in this paper.

Here, we consider the multiterm time fractional differential operator which has the subdiffusion process (see [16]). It is different from (2), which only has one integer order differential operator in time.

Note that the analytical solutions for MT-TS-RFADEs have been studied in [37], in which this problem is well defined. For this problem, some new techniques have been used, such as a spectral representation of the fractional Laplacian operator and the equivalent relationship between the fractional Laplacian operator and the Riesz fractional derivative.

For convenience, we introduce the following definitions and properties. The space derivatives and are the Riesz space fractional derivatives of order β and γ, respectively. The definitions of them can be found in [40].

Let Γ(·) denote the gamma function. For any positive integer n and real number θ (n − 1 < θ < n), there are different definitions of fractional derivatives with order θ in [8]. During this paper, we consider the left, (right) Caputo derivative and left (right) Riemann-Liouville derivative defined as follows:

(i)
the left Caputo derivative:
()
(ii)
the right Caputo derivative:
()
(iii)
the left Riemann-Liouville derivative:
()
(iv)
the right Riemann-Liouville derivative:
()

The Riesz fractional operators and in (5) can be defined by the left and the right Riemann-Liouville fractional derivatives.

Definition 1 (see [40].)The Riesz fractional derivatives of order θ for n ∈ N, n − 1 < θ < n, on a finite interval 0 ≤ x ≤ X is defined as

()

where C_θ = 1/(2cos (πθ/2)).

The multiterm fractional operator P(₀D_t) in (5) is

()

where 0 < α_s < α_s−1 < ⋯<α₁ < α < 1 or 1 < α_s < α_s−1 < ⋯<α₁ < α < 2 or

, and a_i ∈ R, i = 1, …, s, s ∈ N. Here,

and

denote the left Caputo fractional derivatives with respect to the time variable t of order 0 < α < 1 and 0 < α_s < ⋯<α₁ < 1. There are three cases for multiterm time-space fractional derivatives.

Case 1. If 0 < α_s < ⋯<α₁ < α < 1, (5) is a generalized MT-TS-RFADE with multiterm time fractional diffusion terms with initial conditions given as (6). And especially, if α_i = 0, i = 1, …, s and α = 1, then (5) becomes a space fractional advection-diffusion equation with the Riesz space fractional derivatives, which was discussed by Yang et al. [25].

Case 2. If 1 < α_s < ⋯<α₁ < α < 2, (5) is a generalized MT-TS-RFADE with multiterm time fractional wave terms. In this case, the initial conditions are given as follows:

()

Case 3. If , (5) becomes a generalized MT-TS-RFADE, which we refer to as a multiterm time-space fractional mixed wave-diffusion equation. In this case, the initial conditions are also given by (13).

In this paper, we just consider Case 1 of (5) with 0 < α_s < ⋯<α₁ < α < 1. Another two cases with 1 < α_s < ⋯<α₁ < α < 2 and will be studied in our following work.

In order to establish the weak formulation of the problem (5), we need some preparatory work. We use definitions of functional spaces and derive some properties related to these spaces. Let C^∞(0, T) denote the space of infinitely differentiable functions on (0, T), and let

denote the space of infinitely differentiable functions with compact support in (0, T). Let L₂(𝒬) be the space of measurable functions whose square is the Lebesgue integrable in 𝒬, which may denote a domain 𝒬 = I or Ω or I × Ω, where I = [0, T] denotes the time domain and Ω = [0, X] denotes the space domain. The inner product and norm of L₂(𝒬) are defined by

()

For any real σ > 0, we define the spaces

and

to be the closure of

with respect to the norms

and

, respectively, where

()

In the usual Sobolev space

, we also have the definition

()

From [18], for σ > 0, σ ≠ n − 1/2, the spaces

, and

are equal, and their seminorms are all equivalent to

We now give some results for fractional operators on these spaces.

Lemma 2 (see [8], [18].)(1) For real 0 < θ < 1, 0 < δ < 1, if v(0) = 0, x ∈ (0, X), then

()

(2) Let 0 < θ < 1. Then, one has

()

Lemma 3 (see [18].)Let 0 < θ < 2, θ ≠ 1. Then, for any , then

()

Following from the definitions and lemmas above, we define the space

()

when 0 < α_s < ⋯<α₁ < α < 1, 0 < β < 1 and 1 < γ < 2.

Then, one obtains

()

Here, B^α/2,γ/2(I × Ω) is a Banach space with respect to the following norm:

()

where

()

endowed with the norm

()

For obtaining a suitable weak solution for problem (5) with the Caputo time fractional derivation, we consider the connection between the Caputo and the Riemann-Liouville fractional definition. Based on the definitions of the Caputo and the Riemann-Liouville fractional differential operators, we have an immediate consequence, for any real order θ > 0, in [38],

()

where T_n−1[f; 0](t) denotes the Taylor polynomial for f of order n − 1, centered at 0,

()

where f(t) ∈ Cⁿ⁻¹[0, T].

Based on (25), we make

()

Therefore, that led to the following weak formulation of (5). Let B^α/2,γ/2(I×Ω)^′ be the dual space of B^α/2,γ/2(I × Ω). For

, we find u(t, x) ∈ B^α/2,γ/2(I × Ω) such that

()

where the bilinear form 𝒜(·, ·) is, based on Lemmas 2 and 3,

()

and the functional ℱ(·) is given by

()

Lemma 4 (see [17].)For real θ > 0, , then

()

Based on Lemma 4, we can prove the following existence and uniqueness theorem. During this paper, we use the expression A≲B (A ≳ B) to mean that there exists a positive real number c such that A ≤ cB (A ≥ cB). At the same time, we denote A≅B to mean that A≲B≲A, which means there exist positive real numbers c₁, c₂ such that A ≤ c₁B and B ≤ c₂A (i.e., (1/c₁)A ≤ B ≤ c₂A).

Theorem 5. Assume that 0 < α₁ < ⋯<α_s < α < 1, 0 < β < 1, 1 < γ < 2 and f ∈ B^α/2,γ/2(I×Ω)^′. Then, system (28) has a unique solution in B^α/2,γ/2(I × Ω). Furthermore,

()

Proof. The existence and uniqueness of the solution is guaranteed by the well-known Lax-Milgram theorem. First, from the equivalence of , , and , for all u, v ∈ B^α/2,γ/2(I × Ω), it follows that

()

This implies the continuity of the bilinear form 𝒜(·, ·) and the right-hand side function ℱ(v).

We next prove the coercivity of the bilinear operator 𝒜(·, ·). Note that

()

for all

, where

is the extension of φ by zero outside of (0, T). Thus, we find that

is nonnegative for v ∈ H^α/2(0, T), 0 < α < 1 since cos (πα/2) is nonnegative for 0 < α < 1. That is the same for fractional operators with α_i, i = 1, …, s.

From the above analysis, we have

()

By using the well-known Lax-Milgram theorem, there exists a unique solution u ∈ B^α/2,γ/2(I × Ω) such that (28) holds.

To prove the stability estimate (32), by using (34) and (36), we take v = u in (28) and obtain

()

which implies that

3. Time Discretization

In this section, we consider the Diethelm fractional backward difference method based on quadrature, which was independently introduced by [39], for ordinary fractional differential equations. Here, we consider this method for the time discretization of (5) and derive the convergence rate for the time-discretization of MT-TS-RFADEs.

Lemma 6 (see [25].)For n − 1 < θ < n (n = 1,2, …) and a function u(x) defined on an unbounded domain (−∞ < x < ∞), the following equality holds:

()

where Δ is the Laplacian.

Definition 7 (see [26].)Suppose the Laplacian has a complete set of orthonormal eigenfunctions ϕ_n corresponding to eigenvalues on a bounded region 𝒬, that is, on a bounded region 𝒬; B(ϕ) = 0 on ∂𝒬 is one of the standard three homogeneous boundary conditions. Let

()

then for any f ∈ F, (−Δ) ^θ/2 is defined by

()

Here, for any t ∈ I, we make a continuous prolongation in space for function u(t, x) as follows:

()

Let u(t) denote the one-variable function of

, and let f(t) and u(0) denote the one-variable functions as f(t, ·) and

, respectively. By the definition (12) of P(₀D_t) and Lemma 6, (5) is equivalent to

()

Let A = −Δ,

. Then, the system (5) and the initial condition (6) can be rewritten in the abstract form, for 0 ≤ t ≤ T,

()

Based on (25), (43) can be rewritten as

()

where 0 < t < T, 0 < α_s < ⋯<α₁ < α < 1.

Let 0 = t₀ < t₁ < ⋯<t_N = T be a partition of [0, T]. Without loss of generality, for 0 < α < 1 and fix t_n,n = 1,2, …, N, we have

()

where g(θ) = u(t_j − t_jθ) − ϕ₀. Here, the integral is a Hadamard finite-part integral, in [38, 39].

Now, for every n, we replace the integral by a first-degree compound quadrature formula with equispaced nodes 0,1/n, 2/n, …, 1 and obtain

()

where the weights

are

()

and the remainder term

satisfies

()

where γ_α > 0 is a constant.

Thus, we have

()

where

Let t = t_n, we can write (45) as

()

for n = 1,2, 3, …, where

Denote Uⁿ as the approximation of u(t_n). We can define the following time stepping method:

()

where f_n = f(t_n).

Lemma 8 (see [38].)For 0 < α < 1, let the sequence {d_j} j = 1,2, … be given by d₁ = 1 and . Then, 1 ≤ d_j ≤ (sin(πα))/(πα(1 − α))j^α, j = 1,2, 3, ….

Let eⁿ = Uⁿ − u(t_n) denote the error in t_n. Let ∥·∥ be any given norm. Then, we have the following error estimate.

Theorem 9. Let u(t_n) and Uⁿ be the solutions of (43) and (52), respectively, and Δt is the time step size. Then, one has

()

Proof. Subtracting (52) from (51), we obtain the error equation

()

Note that e⁰ = ϕ₀ − U⁰ = 0 and denote

()

Thus, we have

()

From Definition 7, note that A is a positive definite elliptic operator with all of eigenvalues λ > 0. Since and Γ(−α) < 0 when 0 < α < 1, we have

()

Hence,

()

Note that e⁰ = ϕ₀ − U⁰ = 0. Denote d₁ = 1 and

()

Then, by induction and Lemma 8, we have

()

4. Space Discretization

In this section, we consider the space discretization of (5) with homogeneous boundary condition. Using the FEM, we obtain the numerical approximation solution in a finite domain. Then, we prove the convergence rate of this method. Let Ω = [0, X] be an interval in one-dimensional space. All of the results in this section can be generalized into the cases of high dimension.

Based on the time discretization in Section 3 and (25), we need to find

such that

()

Let h denote the maximal length of intervals in Ω, and let r be any nonnegative integer. We denote the norm in H^r(Ω) by

. Let

be a family of finite element space with the accuracy of order r ≥ 2; that is, S_h consists of continuous functions on the closure

of Ω which are polynomials of degree at most r − 1 in each interval and which vanish outside Ω_h such that for small h,

()

The semidiscrete problem of (5) is to find the approximate solution u_h(t) = u_h(t, ·) ∈ S_h for each t such that

()

Let R_h : H^γ/2(Ω) → S_h be the elliptic projection defined by

()

Lemma 10. Assume that (62) holds. Then, for R_h defined by (64) and any , one has

()

Proof. Let I_h be the projection operator from to S_h. From the definition of L₂-norm, we obtain

()

Let χ = R_hv − I_hv ∈ S_h. From (64), we obtain

()

Note that

()

Thus, combining (67) and (68), we obtain

()

By (62), we see that

()

By interpolation properties, we obtain

()

Similarly, we have

()

Combining (71) and (72), we can obtain (65).

Theorem 11. For 0 < α_s < ⋯<α₁ < α < 1, let u_h and u be the solutions of (63) and (61), respectively. Then, it holds

()

Proof. We write

()

where ϑ = u_h − R_hu, ρ = R_hu − u. The second term is easily bounded by Lemma 10 and has the obvious estimate

()

In order to estimate ϑ, for all χ ∈ S_h, we get

()

Choosing χ = ϑ(t) and integrating on both sides with respect to t on [0, T], we obtain

()

By Lemmas 2–4, for any small ϵ > 0, we have

()

where C_ϵ is a constant respect to ϵ, A_α = cos (πα/2) and

For sufficiently small ϵ > 0, by (75), we obtain

()

Combining (75) with (79), we obtain that

()

For the reason that the time and space fractional derivatives, we introduce the complete form of this FEM. In view of space discretization, we first pose the finite-dimensional problem to find u_h(t, ·) ∈ S_h such that (63) holds.

In terms of the basis

, write

, and insert it into (63). After the time discretization on t_n, in Section 3, we get

()

To obtain the value of

, Let

. From (81), we obtain a vector equation

()

where

is the mass matrix;

and

are stiffness matrices with θ = β/2, γ/2, as follows:

()

and

is a vector valued function. Then, from (82), we can obtain the solution U_n.

5. Stability of the Numerical Method

In this section, we analyze the stability of the FEM for MT-TS-RFADEs (5). Now, we do some preparation before proof. Based on the definition of coefficients in Section 3, we can obtain the following lemma easily.

Lemma 12. For 0 < α < 1, the coefficients , (k = 1, …, n) satisfy the following properties:

(i)
and for k = 1,2, …, n,
(ii)
.

Now, we report the stability theorem of this FEM for MT-TS-RFADEs as follows.

Theorem 13. The FEM defined in (81) is unconditionally stable.

Proof. Let Uⁿ denote the approximation to u_h at t = t_n and χ(·) = Uⁿ(·) and the right-hand side . From (63), we have

()

Using the Cauchy-Schwarz inequality,

for k = 0,1, 2, …, n, by Definition 1 and Lemma 12, we obtain

()

We prove the stability of (63) by induction. From the beginning, we have

()

The induction basis

is presupposed. For the induction step, we have

. Then, using this result, by Lemma 12, we obtain

()

Here, 0 < 1 − α < 1 and 0 < 1 − α_i < 1 for i = 1, …, s. After squaring at both sides of the above inequality, we obtain

6. Numerical Tests

Based on the above analysis, we present three numerical examples for MT-TS-RFADEs to demonstrate the efficiency of our theoretical analysis. The main purpose is to check the convergence behavior of numerical solutions with respect to time step size Δt and space step size Δx, which have been shown in Theorems 9 and 11.

Example 1. Consider MT-TS-RFADE, in t ∈ [0,0.5], x ∈ [0,1],

()

The exact solution of (88) is u(t, x) = (2t − 1) ²x²(1 − x) ². From the definition of the Riemann-Liouville differential operator, it holds

()

where a is a positive constant. From (89), we can choose right-hand side function f(t, x) to satisfy (88).

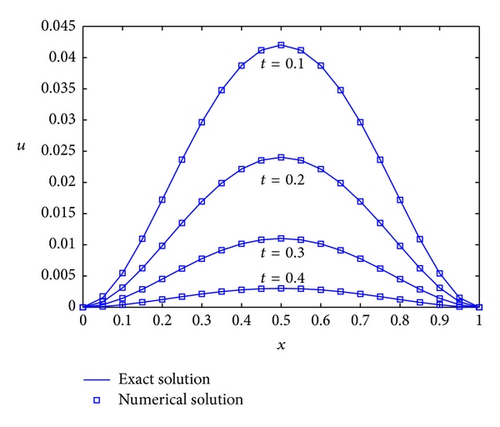
Choosing α = 0.9 and α₁ = 0.2 in time fractional operators and β = 0.4γ = 1.6 in the space Riesz fractional operators, we can obtain the numerical approximation to the exact solution of (88) on finite domain [0,0.5]×[0,1], with space step size Δx = 0.05 and time step size Δt = 0.01. In Figure 1, one can see that the numerical solution matches well with the exact solution.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Numerical solution and exact solution for Example 1.

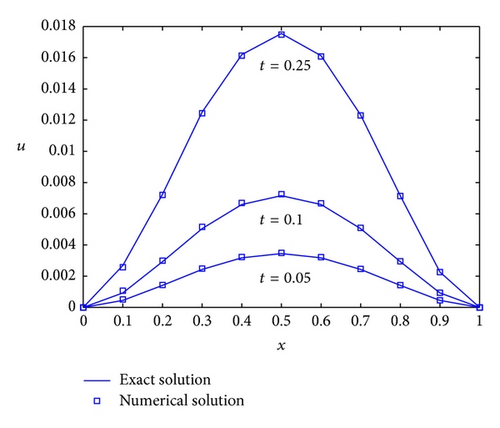
Example 2. Consider MT-TS-RFADE (88) with conditions as follows:

()

Let the exact solution is u(t, x) = t^0.9x²(1 − x) ². We choose α₁ = 0.3, α = 0.4, β = 0.4, γ = 1.7 and obtain the numerical solution and exact solution when t = 0.05,0.1,0.25. The results have been shown in Figure 2, where the exact solution is noted by lines and numerical solution is noted by squares. Here, space step size is Δx = 0.1; time step size is Δt = 0.01.

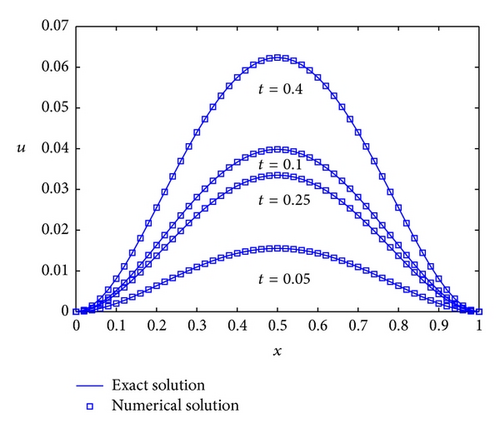
Example 3. Consider MT-TS-RFADE (88) with the zero Dirichlet boundary conditions, for t ∈ [0,1], x ∈ [0,1]. We require that the exact solution is u(t, x) = sin(2πt)x²(1 − x) ².

For this example, in the first test, we obtain the numerical solution and exact solution when t = 0.05, 0.1, 0.25, 0.4 in Figure 3, where we choose time step size Δt = 0.01 and space step size Δx = 0.01 with α₁ = 0.3, α = 0.5, and β = 0.9, γ = 1.9.

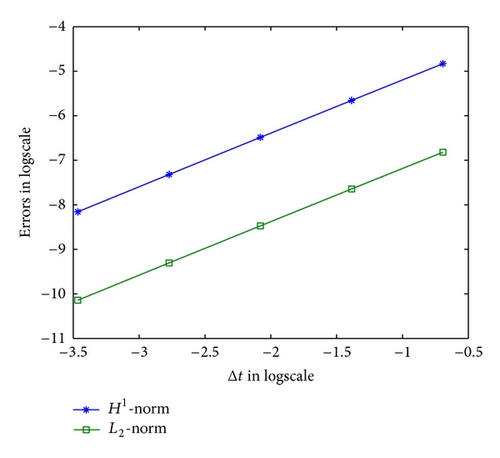
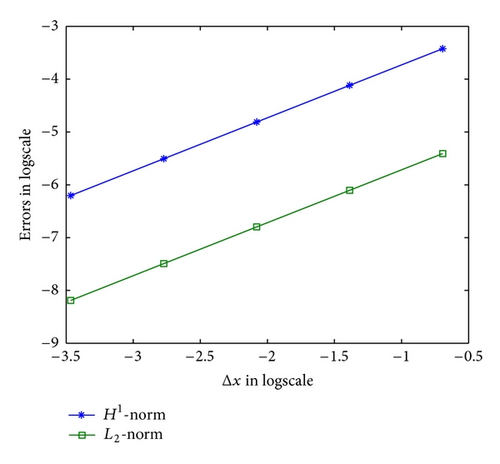
In the second test, we check the convergence rates of numerical solutions with respect to the fractional orders α₁, α, β, and γ. We fix α₁ = 0.2, α = 0.8, β = 0.8, and γ = 1.8 and choose Δx = 0.001 which is small enough such that the space discretization errors are negligible as compared with the time errors. Choosing step size Δt = 1/2ⁱ (i = 1, …, 5), we present Table 1 with the convergence rate which is equal to 1.2, as Theorem 9 predicted. Table 2 shows the spatial approximate convergence rate, by fixing Δt = 0.001 and choosing Δx = 1/2ⁱ (i = 1, …, 5). From Theorem 11, the convergence rate should be equal to or less than 1.1 (i.e., η − γ/2 for η = 2 and γ = 1.8). In Table 2, the numerical results match well with such conclusion. Here, we also report both the L₂-norm and H¹-norm of errors in Figure 4.

Table 1. Convergence rate in time for Example 3.

Δx	Δt	H¹-norm	L₂-norm	cvge. rate
0.001	1/2	7.9601 × 10⁻³	1.0925 × 10⁻³
0.001	1/4	3.4906 × 10⁻³	4.7906 × 10⁻⁴	1.1893
0.001	1/8	1.5238 × 10⁻³	2.0914 × 10⁻⁴	1.1957
0.001	1/16	6.6273 × 10⁻⁴	9.0956 × 10⁻⁵	1.2012
0.001	1/32	2.8667 × 10⁻⁴	3.9343 × 10⁻⁵	1.2090

Table 2. Convergence rate in space for Example 3.

Δt	Δx	H¹-norm	L₂-norm	cvge. rate
0.001	1/2	3.2591 × 10⁻²	4.4731 × 10⁻³
0.001	1/4	1.6288 × 10⁻²	2.2356 × 10⁻³	1.0006
0.001	1/8	8.1364 × 10⁻³	1.1167 × 10⁻³	1.0014
0.001	1/16	4.0602 × 10⁻³	5.5723 × 10⁻⁴	1.0029
0.001	1/32	2.0220 × 10⁻³	2.7751 × 10⁻⁴	1.0057

Acknowledgments

The authors are grateful to the referees for their valuable comments. This work is supported by the National Natural Science Foundation of China (11101109 and 11271102), the Natural Science Foundation of Hei-long-jiang Province of China (A201107), and SRF for ROCS, SEM.

References

1 Metzler R. and Klafter J., The random walk′s guide to anomalous diffusion: a fractional dynamics approach, Physics Reports. (2000) 339, no. 1, 1–77, https://doi.org/10.1016/S0370-1573(00)00070-3, MR1809268, ZBL0984.82032.
10.1016/S0370-1573(00)00070-3
CAS Web of Science® Google Scholar
2 Zaslavsky G. M., Chaos, fractional kinetics, and anomalous transport, Physics Reports. (2002) 371, no. 6, 461–580, https://doi.org/10.1016/S0370-1573(02)00331-9, MR1937584, ZBL0999.82053.
10.1016/S0370-1573(02)00331-9
Web of Science® Google Scholar
3 Metzler R. and Klafter J., The restaurant at the end of the random walk: recent developments in the description of anomalous transport by fractional dynamics, Journal of Physics A. (2004) 37, no. 31, R161–R208, https://doi.org/10.1088/0305-4470/37/31/R01, MR2090004, ZBL1075.82018.
10.1088/0305-4470/37/31/R01
Web of Science® Google Scholar
4 Gloeckle W. G. and Nonnenmacher T. F., Fractional integral operators and Fox functions in the theory of viscoelasticity, Macromolecules. (1991) 24, no. 24, 6426–6434.
10.1021/ma00024a009
CAS Web of Science® Google Scholar
5 Schiessel H., Metzler R., Blumen A., and Nonnenmacher T. F., Generalized vis- coelastic models: their fractional equations with solutions, Journal of Physics A. (1995) 28, no. 23, 6567–6584.
10.1088/0305-4470/28/23/012
CAS Web of Science® Google Scholar
6 Diethelm K., The Analysis of Fractional Differential Equations, 2004, Springer, Berlin, Germany.
Google Scholar
7 Hilfer E., Applications of Fractional Calculus in Physics, 2000, World Scientific Publishing, New York, NY, USA, https://doi.org/10.1142/9789812817747, MR1890104.
10.1142/3779
Google Scholar
8 Podlubny I., Fractional Differential Equations, 1999, Academic Press, San Diego, Calif, USA, MR1658022.
Web of Science® Google Scholar
9 Samko S. G., Kilbas A. A., and Marichev O. I., Fractional Integrals and Derivatives: Theory and Applications, 1993, Gordon and Breach Science Publishers, Philadelphia, Pa, USA, MR1347689.
Google Scholar
10 Adolfsson K., Enelund M., and Larsson S., Adaptive discretization of an integro-differential equation with a weakly singular convolution kernel, Computer Methods in Applied Mechanics and Engineering. (2003) 192, no. 51-52, 5285–5304, https://doi.org/10.1016/j.cma.2003.09.001, MR2023899, ZBL1042.65103.
10.1016/j.cma.2003.09.001
Web of Science® Google Scholar
11 Adolfsson K., Enelund M., and Larsson S., Adaptive discretization of fractional order viscoelasticity using sparse time history, Computer Methods in Applied Mechanics and Engineering. (2004) 193, no. 42–44, 4567–4590, https://doi.org/10.1016/j.cma.2004.03.006, MR2091119, ZBL1112.74495.
10.1016/j.cma.2004.03.006
Web of Science® Google Scholar
12 Roop J. P., Computational aspects of FEM approximation of fractional advection dispersion equations on bounded domains in R², Journal of Computational and Applied Mathematics. (2006) 193, no. 1, 243–268, https://doi.org/10.1016/j.cam.2005.06.005, MR2228717, ZBL1092.65122.
10.1016/j.cam.2005.06.005
Web of Science® Google Scholar
13 Ervin V. J. and Roop J. P., Variational formulation for the stationary fractional advection dispersion equation, Numerical Methods for Partial Differential Equations. (2006) 22, no. 3, 558–576, https://doi.org/10.1002/num.20112, MR2212226, ZBL1095.65118.
10.1002/num.20112
Web of Science® Google Scholar
14 Ervin V. J. and Roop J. P., Variational solution of fractional advection dispersion equations on bounded domains in R^d, Numerical Methods for Partial Differential Equations. (2007) 23, no. 2, 256–281, https://doi.org/10.1002/num.20169, MR2289452, ZBL1117.65169.
10.1002/num.20169
Web of Science® Google Scholar
15 Ervin V. J., Heuer N., and Roop J. P., Numerical approximation of a time dependent, nonlinear, space-fractional diffusion equation, SIAM Journal on Numerical Analysis. (2007) 45, no. 2, 572–591, https://doi.org/10.1137/050642757, MR2300288, ZBL1141.65089.
10.1137/050642757
Web of Science® Google Scholar
16 Li C., Zhao Z., and Chen Y., Numerical approximation of nonlinear fractional differential equations with subdiffusion and superdiffusion, Computers & Mathematics with Applications. (2011) 62, no. 3, 855–875, https://doi.org/10.1016/j.camwa.2011.02.045, MR2824676, ZBL1228.65190.
10.1016/j.camwa.2011.02.045
Web of Science® Google Scholar
17 Li X. J. and Xu C. J., A space-time spectral method for the time fractional diffusion equation, SIAM Journal on Numerical Analysis. (2009) 47, no. 3, 2108–2131, https://doi.org/10.1137/080718942, MR2519596, ZBL1193.35243.
10.1137/080718942
Web of Science® Google Scholar
18 Li X. J. and Xu C. J., Existence and uniqueness of the weak solution of the space-time fractional diffusion equation and a spectral method approximation, Communications in Computational Physics. (2010) 8, no. 5, 1016–1051, https://doi.org/10.4208/cicp.020709.221209a, MR2674276.
10.4208/cicp.020709.221209a
Web of Science® Google Scholar
19 Jiang Y. and Ma J., High-order finite element methods for time-fractional partial differential equations, Journal of Computational and Applied Mathematics. (2011) 235, no. 11, 3285–3290, https://doi.org/10.1016/j.cam.2011.01.011, MR2784043, ZBL1216.65130.
10.1016/j.cam.2011.01.011
Web of Science® Google Scholar
20 Ford N. J., Xiao J., and Yan Y., A finite element method for time fractional partial differential equations, Fractional Calculus and Applied Analysis. (2011) 14, no. 3, 454–474, https://doi.org/10.2478/s13540-011-0028-2, MR2837641.
10.2478/s13540-011-0028-2
Web of Science® Google Scholar
21 Park Y. S. and Baik J. J., Analytical solution of the advection-diffusion equation for a ground-level finite area source, Atmospheric Environment. (2008) 42, no. 40, 9063–9069.
10.1016/j.atmosenv.2008.09.019
CAS Web of Science® Google Scholar
22 Saichev A. I. and Zaslavsky G. M., Fractional kinetic equations: solutions and applications, Chaos. (1997) 7, no. 4, 753–764, https://doi.org/10.1063/1.166272, MR1604710, ZBL0933.37029.
10.1063/1.166272
CAS PubMed Web of Science® Google Scholar
23 Zaslavsky G. M., Chaos, fractional kinetics, and anomalous transport, Physics Reports. (2002) 371, no. 6, 461–580, https://doi.org/10.1016/S0370-1573(02)00331-9, MR1937584, ZBL0999.82053.
10.1016/S0370-1573(02)00331-9
Web of Science® Google Scholar
24 Ciesielski M. and Leszczynski J., Numerical solutions of a boundary value problem for the anomalous diffusion equation with the Riesz fractional derivative, Proceedings of the 16th International Conference on Computer Methods in Mechanics, 2005, 21–24.
Google Scholar
25 Yang Q., Liu F., and Turner I., Numerical methods for fractional partial differential equations with Riesz space fractional derivatives, Applied Mathematical Modelling. (2010) 34, no. 1, 200–218, https://doi.org/10.1016/j.apm.2009.04.006, MR2566688, ZBL1185.65200.
10.1016/j.apm.2009.04.006
Web of Science® Google Scholar
26 Shen S., Liu F., Anh V., and Turner I., The fundamental solution and numerical solution of the Riesz fractional advection-dispersion equation, IMA Journal of Applied Mathematics. (2008) 73, no. 6, 850–872, https://doi.org/10.1093/imamat/hxn033, MR2461708, ZBL1179.37073.
10.1093/imamat/hxn033
Web of Science® Google Scholar
27 Shen S., Liu F., and Anh V., Numerical approximations and solution techniques for the space-time Riesz-Caputo fractional advection-diffusion equation, Numerical Algorithms. (2011) 56, no. 3, 383–403, https://doi.org/10.1007/s11075-010-9393-x, MR2774121, ZBL1214.65046.
10.1007/s11075-010-9393-x
Web of Science® Google Scholar
28 Diethelm K. and Ford N. J., Numerical solution of the Bagley-Torvik equation, BIT Numerical Mathematics. (2002) 42, no. 3, 490–507, MR1931882, ZBL1035.65067.
10.1023/A:1021973025166
Web of Science® Google Scholar
29 Erturk V. S., Momani S., and Odibat Z., Application of generalized differential transform method to multi-order fractional differential equations, Communications in Nonlinear Science and Numerical Simulation. (2008) 13, no. 8, 1642–1654, https://doi.org/10.1016/j.cnsns.2007.02.006, MR2398696, ZBL1221.34022.
10.1016/j.cnsns.2007.02.006
Web of Science® Google Scholar
30 Diethelm K. and Ford N. J., Multi-order fractional differential equations and their numerical solution, Applied Mathematics and Computation. (2004) 154, no. 3, 621–640, https://doi.org/10.1016/S0096-3003(03)00739-2, MR2072809, ZBL1060.65070.
10.1016/S0096-3003(03)00739-2
Web of Science® Google Scholar
31 Doha E. H., Bhrawy A. H., and Ezz-Eldien S. S., Efficient Chebyshev spectral methods for solving multi-term fractional orders differential equations, Applied Mathematical Modelling. (2011) 35, no. 12, 5662–5672, https://doi.org/10.1016/j.apm.2011.05.011, MR2820942, ZBL1228.65126.
10.1016/j.apm.2011.05.011
Web of Science® Google Scholar
32 Momani S., A numerical scheme for the solution of multi-order fractional differential equations, Applied Mathematics and Computation. (2006) 182, no. 1, 761–770, https://doi.org/10.1016/j.amc.2006.04.037, MR2292084, ZBL1107.65119.
10.1016/j.amc.2006.04.037
Web of Science® Google Scholar
33 Daftardar-Gejji V. and Bhalekar S., Boundary value problems for multi-term fractional differential equations, Journal of Mathematical Analysis and Applications. (2008) 345, no. 2, 754–765, https://doi.org/10.1016/j.jmaa.2008.04.065, MR2429175, ZBL1151.26004.
10.1016/j.jmaa.2008.04.065
Web of Science® Google Scholar
34 Golbabai A. and Sayevand K., Analytical modelling of fractional advection-dispersion equation defined in a bounded space domain, Mathematical and Computer Modelling. (2011) 53, no. 9-10, 1708–1718, https://doi.org/10.1016/j.mcm.2010.12.046, MR2782857, ZBL1219.76035.
10.1016/j.mcm.2010.12.046
Web of Science® Google Scholar
35 Jiang H., Liu F., Turner I., and Burrage K., Analytical solutions for the multi-term time-fractional diffusion-wave/diffusion equations in a finite domain, Computers & Mathematics with Applications. (2012) 64, no. 10, 3377–3388, https://doi.org/10.1016/j.camwa.2012.02.042, MR2989366.
10.1016/j.camwa.2012.02.042
Web of Science® Google Scholar
36 Liu F., Meerschaert M. M., McGough R. J., Zhuang P., and Liu Q., Numerical methods for solving the multi-term time-fractional wave-diffusion equation, Fractional Calculus and Applied Analysis. (2013) 16, no. 1, 9–25, https://doi.org/10.2478/s13540-013-0002-2, MR3016639.
10.2478/s13540-013-0002-2
CAS PubMed Web of Science® Google Scholar
37 Jiang H., Liu F., Turner I., and Burrage K., Analytical solutions for the multi-term time-space Caputo-Riesz fractional advection-diffusion equations on a finite domain, Journal of Mathematical Analysis and Applications. (2012) 389, no. 2, 1117–1127, https://doi.org/10.1016/j.jmaa.2011.12.055, MR2879284, ZBL1234.35300.
10.1016/j.jmaa.2011.12.055
Web of Science® Google Scholar
38 Diethelm K., Generalized compound quadrature formulae for finite-part integrals, IMA Journal of Numerical Analysis. (1997) 17, no. 3, 479–493, https://doi.org/10.1093/imanum/17.3.479, MR1459334, ZBL0871.41021.
10.1093/imanum/17.3.479
Web of Science® Google Scholar
39 Diethelm K., An algorithm for the numerical solution of differential equations of fractional order, Electronic Transactions on Numerical Analysis. (1997) 5, no. 1, 1–6, MR1447831, ZBL0890.65071.
Google Scholar
40 Gorenflo R. and Mainardi F., Random walk models for space-fractional diffusion processes, Fractional Calculus & Applied Analysis. (1998) 1, no. 2, 167–191, MR1656314, ZBL0946.60039.
Google Scholar

Citing Literature

All articles

A Finite Element Method for the Multiterm Time-Space Riesz Fractional Advection-Diffusion Equations in Finite Domain

Abstract

1. Introduction

2. Existence and Uniqueness

3. Time Discretization

4. Space Discretization

5. Stability of the Numerical Method

6. Numerical Tests

Acknowledgments

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

A Finite Element Method for the Multiterm Time-Space Riesz Fractional Advection-Diffusion Equations in Finite Domain

Abstract

1. Introduction

2. Existence and Uniqueness

3. Time Discretization

4. Space Discretization

5. Stability of the Numerical Method

6. Numerical Tests

Acknowledgments

References

Citing Literature

Figures

References

Related

Information