The integral representations of the solution around the vertices of the interior reentered angles (on the “singular” parts) are approximated by the composite midpoint rule when the boundary functions are from C^4,λ, 0 < λ < 1. These approximations are connected with the 9-point approximation of Laplace′s equation on each rectangular grid on the “nonsingular” part of the polygon by the fourth-order gluing operator. It is proved that the uniform error is of order O(h⁴ + ε), where ε > 0 and h is the mesh step. For the p-order derivatives (p = 0,1, …) of the difference between the approximate and the exact solutions, in each “ singular” part order is obtained; here r_j is the distance from the current point to the vertex in question and α_jπ is the value of the interior angle of the jth vertex. Numerical results are given in the last section to support the theoretical results.

1. Introduction

In the last two decades, among different approaches to solve the elliptic boundary value problems with singularities, a special emphasis has been placed on the construction of combined methods, in which differential properties of the solution in different parts of the domain are used (see [1, 2], and references therein).

In [2–7], a new combined difference-analytical method, called the block-grid method (BGM), is proposed for the solution of the Laplace equation on polygons, when the boundary functions on the sides causing the singular vertices are given as algebraic polynomials of the arc length. In the BGM, the given polygon is covered by a finite number of overlapping sectors around the singular vertices (“singular” parts) and rectangles for the part of the polygon which lies at a positive distance from these vertices (“nonsingular” part). The special integral representation in each “singular” part is approximated, and they are connected by the appropriate order gluing operator with the finite difference equations used in the “nonsingular” part of the polygon.

In [8, 9], the restriction on the boundary functions to be algebraic polynomials on the sides of the polygon causing the singular vertices in the BGM was removed. It was assumed that the boundary function on each side of the polygon is given from the Hölder classes C^k,λ, 0 < λ < 1, and on the “nonsingular” part the 5-point scheme is used when k = 2 [8] and the 9-point scheme is used when k = 6 [9]. For the 5-point scheme a simple linear interpolation with 4 points is used. For the 9-point scheme an interpolation with 31 points is used to construct a gluing operator connecting the subsystems. Moreover, to connect the quadrature nodes which are at a distance of less than 4h from boundary of the polygon, a special representation of the harmonic function through the integrals of Poisson type for a half plane is used (see [9]).

In this paper the BGM is developed for the Dirichlet problem when the boundary function on each side of the polygon is from C^4,λ, by using the 9-point scheme on the “nonsingular” part with 16-point gluing operator for all quadrature nodes, including those near the boundary. The paper is organized as follows: in Section 2, the boundary value problem and the integral representations of the exact solution in each “singular” part are given. In Section 3, to support the aim of the paper, a Dirichlet problem on the rectangle for the known exact solution from C^k,λ, k = 3,4, is solved using the 9-point scheme and the numerical results are illustrated. In Section 4, the system of block-grid equations and the convergence theorems are given. In Section 5 a highly accurate approximation of the coefficient of the leading singular term of the exact solution (stress intensity factor) is given. In Section 6 the method is illustrated for solving the problem in L-shaped polygon with the corner singularity. The conclusions are summarized in Section 7.

2. Dirichlet Problem on a Staircase Polygon

Let G be an open simply connected polygon, γ_j, j = 1,2, …, N, its sides, including the ends, enumerated counterclockwise, γ = γ₁ ∪ ⋯∪γ_N the boundary of G, and α_jπ, (α_j = 1/2, 1, 3/2, 2), the interior angle formed by the sides γ_j−1 and γ_j, (γ₀ = γ_N). Denote by A_j = γ_j−1∩γ_j the vertex of the jth angle and by r_j, θ_j a polar system of coordinates with a pole in A_j, where the angle θ_j is taken counterclockwise from the side γ_j.

We consider the boundary value problem

()

where Δ ≡ ∂²/∂x² + ∂²/∂y², φ_j is a given function on γ_j of the arc length s taken along γ, and φ_j ∈ C^4,λ(γ_j), 0 < λ < 1; that is, φ_j has the fourth-order derivative on γ_j, which satisfies a Hölder condition with exponent λ.

At some vertices A_j, (s = s_j) for α_j = 1/2 the conjugation conditions

()

are fulfilled. For the remaining vertices A_j, the values of φ_j−1 and φ_j at A_j might be different. Let E be the set of all j, (1 ≤ j ≤ N) for which α_j ≠ 1/2 or α_j = 1/2, but (2) is not fulfilled. In the neighborhood of A_j, j ∈ E, we construct two fixed block sectors , where 0 < r_j2 < r_j1 < min {s_j+1 − s_j, s_j − s_j−1}, T_j(r) = {(r_j, θ_j) : 0 < r_j < r, 0 < θ_j < α_jπ}.

Let (see [10])

()

where

()

The function Q_j(r_j, θ_j) is harmonic on and satisfies the boundary conditions in (1) on and , j ∈ E, except for the point A_j when φ_j−1(s_j) ≠ φ_j(s_j).

We formally set the value of Q_j(r_j, θ_j) and the solution u of the problem (1) at the vertex A_j equal to (φ_j−1(s_j) + φ_j(s_j))/2, j ∈ E.

Let

()

where

()

is the kernel of the Poisson integral for a unit circle.

Lemma 1 (see [10].)The solution u of the boundary value problem (1) can be represented on , in the form

()

where V_j is the curvilinear part of the boundary of , and Q_j(r_j, θ_j) is the function defined by (4).

3. 9-Point Solution on Rectangles

Let Π = {(x, y) : 0 < x < a, 0 < y < b} be a rectangle, with a/b being rational, γ_j, j = 1,2, 3,4 the sides, including the ends, enumerated counterclockwise, starting from the left side (γ₀ ≡ γ₄, γ₅ ≡ γ₁), and the boundary of Π.

We consider the boundary value problem

()

where φ_j is the given function on γ_j.

Definition 2. One says that the solution u of the problem (9) belongs to if

()

and at the vertices A_j = γ_j−1∩γ_j the conjugation conditions

()

are satisfied.

Remark 3. From Theorem 3.1 in [11] it follows that the class of functions is wider than .

Let h > 0, with a/h ≥ 2, b/h≥2 integers. We assign to Π^h a square net on Π, with step h, obtained with the lines ,y = 0, h, 2h, …. Let

be a set of nodes on the interior of γ_j and let

()

We consider the system of finite difference equations

()

where

()

On the basis of the maximum principle the unique solvability of the system of finite difference equations (13) follows (see [12, Chapter 4]).

Everywhere below we will denote constants which are independent of h and of the cofactors on their right by c, c₀, c₁, …, generally using the same notation for different constants for simplicity.

Theorem 4. Let u be the solution of problem (9). If , then

()

where u_h is the solution of the system (13).

Proof. For the proof of this theorem see [13].

Let Π^′ = {(x, y):−0.25 < x < 0.25, 0 < y < 1} and let γ^′ be the boundary of Π^′. We consider the Dirichlet problem

()

where , is the exact solution of this problem, which is from .

We solve the problem (16) by approximating 9-point scheme when k = 3,4 for the different values of λ.

In Figure 1, the order of numerical convergence

()

of the 9-point solution u_h, for different h = 2^−ϱ and ϱ = 4,5, 6,7, is demonstrated. These results show that the order of numerical convergence, when the exact solution

, depends on k and λ and is O(h⁴) when k = 4, which supports estimation (15). Moreover, this dependence also requires the use of fourth-order gluing operator for all quadrature nodes in the construction of the system of block-grid equations, when the given boundary functions are from the Hölder classes C^4,λ.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Dependence of the approximate solutions for the boundary functions from C^k,λ.

4. System of Block-Grid Equations

In addition to the sectors and (see Section 2) in the neighborhood of each vertex A_j, j ∈ E of the polygon G, we construct two more sectors and , where 0 < r_j4 < r_j3 < r_j2, r_j3 = (r_j2 + r_j4)/2 and , k ≠ l, k, l ∈ E, and let .

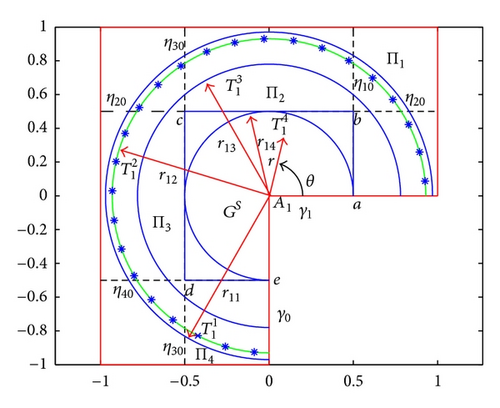
We cover the given solution domain (a staircase polygon) by the finite number of sectors , and rectangles Π_k ⊂ G_T, k = 1,2, …, M, as is shown in Figure 2, for the case of L-shaped polygon, where j = 1, M = 4 (see also [2]). It is assumed that for the sides a_1k and a_2k of Π_k the quotient a_1k/a_2k is rational and . Let η_k be the boundary of the rectangle Π_k, let V_j be the curvilinear part of the boundary of the sector , and let . We choose a natural number n and define the quantities n(j) = max {4, [α_jn]}, β_j = α_jπ/n(j), and . On the arc V_j we take the points , and denote the set of these points by . We introduce the parameter h ∈ (0, ϰ₀/4], where ϰ₀ is a gluing depth of the rectangles Π_k, k = 1,2, …, M, and define a square grid on Π_k, k = 1,2, …, M, with maximal possible step h_k ≤ min {h, min {a_1k, a_2k}/6} such that the boundary η_k lies entirely on the grid lines. Let be the set of grid nodes on Π_k, let be the set of nodes on η_k, and let . We denote the set of nodes on the closure of η_k∩G_T by , the set of nodes on t_kj by , and the set of remaining nodes on η_k by .

Let

()

Let

, where φ_j ∈ C^4,λ(γ_j), 0 < λ < 1, is the given function in (1). We use the matching operator S⁴ at the points of the set ω^h,n constructed in [14]. The value of S⁴(u_h, φ) at the point P ∈ ω^h,n is expressed linearly in terms of the values of u_h at the points P_k of the grid constructed on Π_k(P), (P ∈ Π_k(P)) some part of whose boundary located in G is the maximum distance away from P, and in terms of the boundary values of φ^(m), m = 0,1, 2,3 at a fixed number of points. Moreover S⁴(u_h, 0) has the representation

()

where u_h,k = u_h(P_k),

()

Let

be the set of such points P ∈ ω^h,n, for which all points P_l in expression (19) are in

. If some points P_l in (19) emerge through the side γ_m, then the set of such points P is denoted by

. According to the construction of S⁴ in [14], the expression S⁴(u_h, φ) at each point

can be expressed as follows:

()

where

()

and s_P corresponds to such a point Q ∈ γ_m for which the line PQ is perpendicular to γ_m.

Let

()

The quantities in (24) are given by (4) and (5), which contain integrals that have not been computed exactly in the general case. Assume that approximate values

and

of the quantities in (24) are known with accuracy ε > 0; that is,

()

where j ∈ E, 1 ≤ q ≤ n(j), and c₁, c₂ are constants independent of ε.

Consider the system of linear algebraic equations

()

where 1 ≤ k ≤ M, 1 ≤ m ≤ N, and j ∈ E.

Let

be the sector, where

, and let

, 1 ≤ q ≤ n(j), j ∈ E, be the solution values of the system (26) on

(at the quadrature nodes). The function

()

defined on

, is called an approximate solution of the problem (1) on the closed block

, j ∈ E.

Definition 5. The system (26) and (27) is called the system of block-grid equations.

Theorem 6. There is a natural number n₀, such that for all n ≥ n₀ and for any ε > 0 the system (26) has a unique solution.

Proof. From the estimation (2.29) in [15] follows the existence of the positive constants n₀ and σ, such that for all n ≥ n₀

()

The proof is obtained on the basis of principle of maximum by taking into account (14), (19), (20), and (28).

Theorem 7. There exists a natural number n₀, such that for all

()

where ϰ > 0 is a fixed number, and for any ε > 0 the following inequalities are valid:

()

for integer 1/α_j when p ≥ 1/α_j,

()

for any 1/α_j, if 0 ≤ p < 1/α_j,

()

for noninteger 1/α_j, when p > 1/α_j. Everywhere 0 ≤ q ≤ p, u is the exact solution of the problem (1) and

is defined by formula (27).

Proof. Let

()

where

is a solution of system (26) and u is the trace on

of the solution of (1). On the basis of (1), (26), and (34) the error

satisfies the system of difference equations

()

where 1 ≤ k ≤ M, j ∈ E,

()

On the basis of estimations (15), (21), (25), and Lemma 1 by analogy to the proof of Theorem 4.3 in [9] the proof of inequality (30) follows.

The function given by formula (27), defined on the closed sector , where , and the integral representation (8) of the exact solution of the problem (1) is given on , j ∈ E, and then the difference function is defined on , j ∈ E and

()

On the basis of Lemma 6.11 from [16], (25), and (28), for n ≥ max {n₀, [ln ^1+ϰh⁻¹] + 1}, ϰ > 0 is a fixed number, and we obtain

()

Furthermore, the function

continuous on

is a solution of the following Dirichlet problem:

()

Since

, on the basis of (39) and (40), from Lemma 6.12 in [16], inequalities (31)–(33) of Theorem 7 follow.

5. Stress Intensity Factor

Let, in the condition φ_j ∈ C^4,λ(γ_j), the exponent λ be such that

()

where {·} is the symbol of fractional part. These conditions for the given α_j can be fulfilled by decreasing λ.

On the basis of Section 2 of [11], a solution of the problem (1) can be represented in

, as follows:

()

where

, [·] is the integer part, z = x_j + iy_j,

and

are some numbers, and

is the harmonic on

. By taking θ_j = α_jπ/2, from the formula (43), it follows that the coefficient

which is called the stress intensity factor can be represented as

()

From formula (44) it follows that

can be approximated by

()

Using formula (3), (4), and (27) from (45) for the stress intensity factor (see [17]), we obtain the next formula:

()

This formula is obtained for the second-order BGM in [8].

6. Numerical Results

Let G be L-shaped and defined as follows:

()

where Ω = {(x, y) : 0 ≤ x ≤ 1, − 1 ≤ y ≤ 0} and γ is the boundary of G.

We consider the following problem:

()

where

()

is the exact solution of this problem.

We choose a “singular” part of G as

()

where Ω₁ = {(x, y) : 0 ≤ x ≤ 0.5, − 0.5 ≤ y ≤ 0}. Then G^NS = G∖G^S is a “nonsingular” part of G.

The given domain G is covered by four overlapping rectangles Π_k, k = 1, …, 4, and by the block sector

(see Figure 2). For the boundary of G^S on G is the polygonal line t₁ = abcde. The radius r₁₂ of sector

is taken as 0.93. According to (49), the function Q(r, θ) in (4) is

()

where and . Since we have only one singular point, we omit subindices in (51). We calculate the values Q^ε(r₁₂, θ^q) and Q^ε(r, θ) on the grids , with an accuracy of ε using the quadrature formulae proposed in [10].

On the basis of (46) and (51), for the stress intensity factor, we have

()

Taking the zero approximation

, the results of realization of the Schwarz iteration (see [2]) for the solution of the problem (48) are given in Tables 1, 2, 3, and 4. Tables 1 and 2 represent the order of convergence. Table 6 shows a highly accurate approximation of the stress intensity factor by the proposed fourth order BGM

()

in the “nonsingular” and the order of convergence

()

Table 1. The order of convergence in the “nonsingular” part when h = 2^−ϱ and ε = 5 × 10⁻¹³.

(2^−ϱ, n)
(2⁻⁴, 60)	1.609 × 10⁻⁸	15.577
(2⁻⁵, 170)	1.033 × 10⁻⁹

(2⁻⁵, 130)	1.191 × 10⁻⁹	16.690
(2⁻⁶, 150)	7.136 × 10⁻¹¹

(2⁻⁵, 140)	1.136 × 10⁻⁹	16.259
(2⁻⁶, 170)	6.991 × 10⁻¹¹

(2⁻⁶, 100)	2.169 × 10⁻¹⁰	17.096
(2⁻⁷, 130)	1.269 × 10⁻¹¹

Table 2. The order of convergence in the “singular” part when h = 2^−ϱ and ε = 5 × 10⁻¹³.

(2^−ϱ, n)
(2⁻⁴, 100)	1.931 × 10⁻⁸	16.078
(2⁻⁵, 150)	1.182 × 10⁻⁹

(2⁻⁵, 130)	1.294 × 10⁻⁹	16.789
(2⁻⁶, 150)	7.708 × 10⁻¹¹

(2⁻⁵, 140)	1.312 × 10⁻⁹	17.967
(2⁻⁶, 170)	7.304 × 10⁻¹¹

(2⁻⁶, 100)	2.389 × 10⁻¹⁰	18.164
(2⁻⁷, 130)	1.315 × 10⁻¹¹

Table 3. The minimum errors of the solution over the pairs (h⁻¹, n) in maximum norm when ε = 5 × 10⁻¹³.

(h⁻¹, n)			Iteration
(16,70)	1.139 × 10⁻⁸	1.572 × 10⁻⁸	22
(32,170)	1.033 × 10⁻⁹	1.184 × 10⁻⁹	23
(64,170)	6.990 × 10⁻¹¹	7.304 × 10⁻¹¹	24
(128,200)	8.628 × 10⁻¹²	8.833 × 10⁻¹²	25

Table 4. In G^S∩r ≥ 0.2, the minimum errors of the derivatives over the pairs (h⁻¹, n) in maximum norm when ε = 5 × 10⁻¹³.

(h⁻¹, n)
(16,70)	3.895 × 10⁻⁷	3.895 × 10⁻⁷
(32,170)	4.627 × 10⁻⁸	4.627 × 10⁻⁸
(64,170)	1.124 × 10⁻⁹	3.125 × 10⁻⁹
(128,200)	2.214 × 10⁻¹⁰	2.233 × 10⁻¹⁰

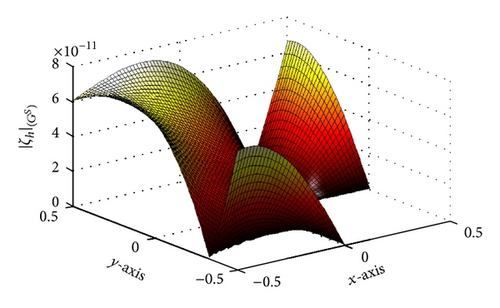
in the “singular” parts of G, respectively, for ε = 5 × 10⁻¹³, where ϱ is a positive integer. In Table 3, the minimal values over the pairs (h⁻¹, n) of the errors in maximum norm, of the approximate solution when ε = 5 × 10⁻¹³, are presented. The similar values of errors for the first-order derivatives are presented in Table 4, when ∂Q/∂x and ∂Q/∂y are approximated by fourth-order central difference formula on G^S for r ≥ 0.2. For r < 0.2, the order of errors decreases down to 10⁻⁶, which are presented in Table 5. This happens because the integrands in (51) are not sufficiently smooth for fourth-order differentiation formula. The order of accuracy of the derivatives for r < 0.2 can be increased if we use similar quadrature rules, which we used for the integrals in (51) for the derivatives of integrands also.

Table 5. In G^S, the minimum errors of the derivatives over the pairs (h⁻¹, n) in maximum norm when ε = 5 × 10⁻¹³.

(h⁻¹, n)
(16,70)	9.663 × 10⁻⁶	9.663 × 10⁻⁶
(32,170)	9.653 × 10⁻⁶	9.653 × 10⁻⁶
(64,170)	9.649 × 10⁻⁶	9.649 × 10⁻⁶
(128,200)	9.648 × 10⁻⁶	9.648 × 10⁻⁶

Table 6. The stress intensity factor

for n = 70, 170, 200 when ε = 5 × 10⁻¹³.

h⁻¹
16	1.000000014856688	1.000000017180415	1.000000017197438
32	1.000000005800844	1.000000001230267	1.000000001236709
64	1.000000004138169	1.000000000073107	1.000000000079938
128	1.000000004053153	1.000000000003531	1.000000000003267

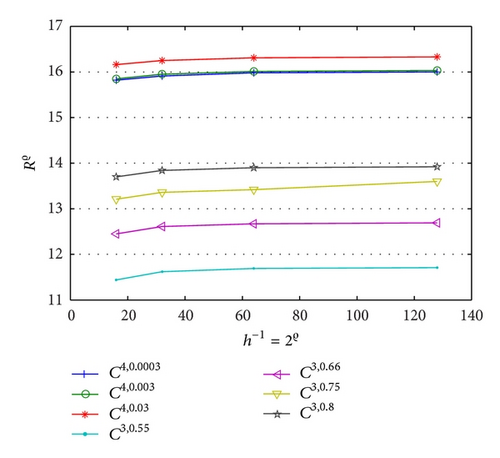
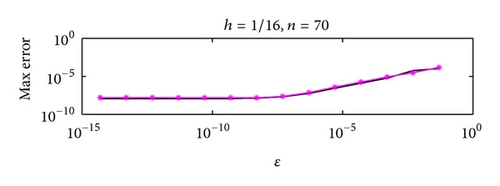
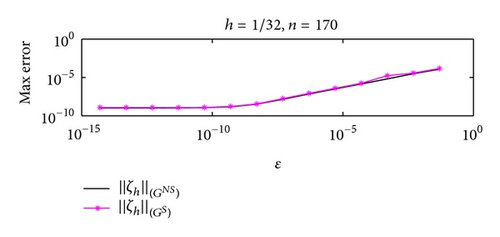
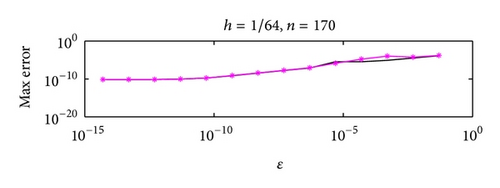
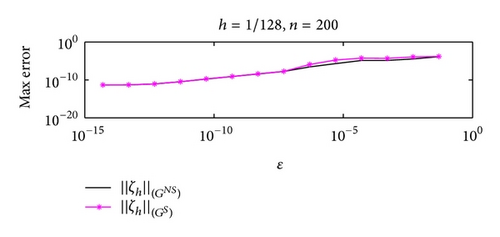
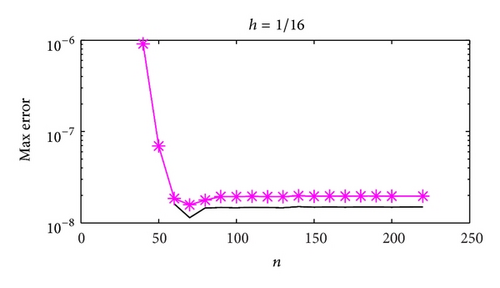
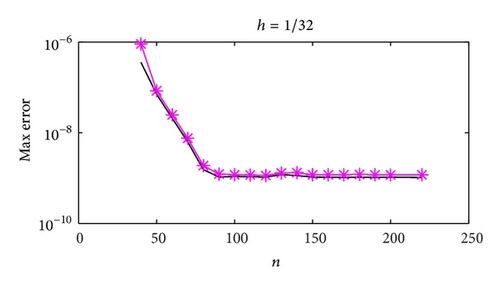
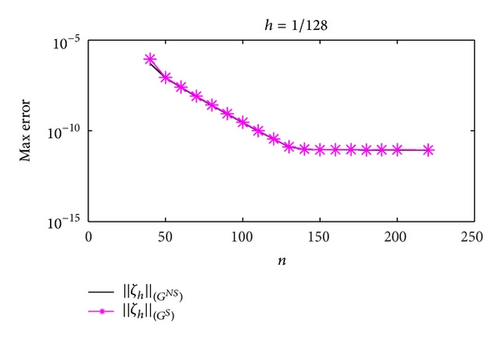
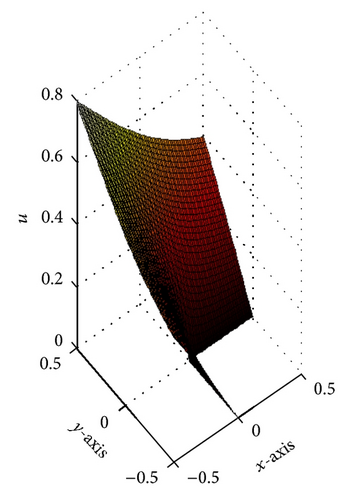
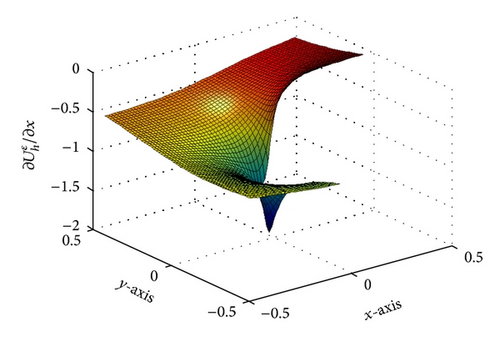
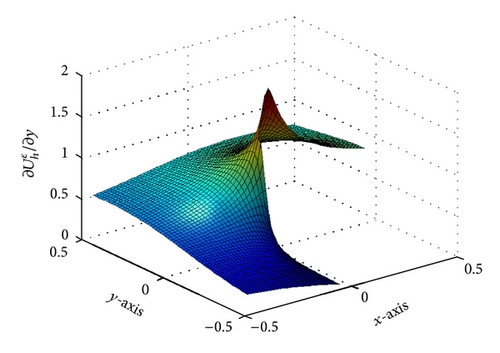
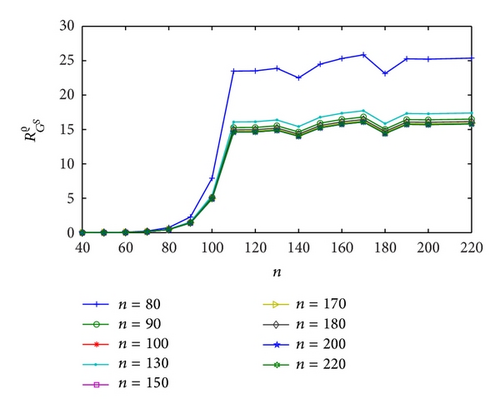
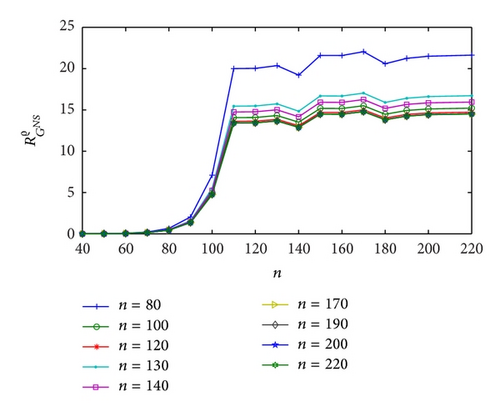
Figures 3 and 4 show the dependence on ε for different mesh steps h. Figure 5 demonstrates the convergence of the BGM with respect to the number of quadrature nodes for different mesh steps h. The approximate solution and the exact solution in the “singular” part are given in Figure 6, to illustrate the accuracy of the BGM. The error of the block-grid solution, when the function Q(r, θ) in (51) is calculated with an accuracy of ε = 5 × 10⁻¹³, is presented in Figure 7. Figures 8 and 9 show the singular behaviour of the first-order partial derivatives in the “singular” part. The ratios and , when ϱ = 5 with respect to different n values for h⁻¹ = 64 and for a fixed value of n of h⁻¹ = 32, are illustrated in Figures 10 and 11, respectively. These ratios show that the order of the convergence in both the “singular” and the “nonsingular” parts is asymptotically equal to 16 when n is kept fixed for h⁻¹ = 32, and it is selected as large as possible (n > 100) for h⁻¹ = 64.

7. Conclusions

In the block-grid method (BGM) for solving Laplace′s equation, the restriction on the boundary functions to be algebraic polynomials on the sides of the polygon causing the singular vertices is removed. This condition is replaced by the functions from the Hölder classes C^4,λ, 0 < λ < 1. In the integral representations around singular vertices (on the “singular” part), which are combined with the 9-point finite difference equations on the “nonsingular” part of the polygon, the boundary conditions are taken into account with the help of integrals of Poisson type for a half-plane. To connect the subsystems, a homogeneous fourth-order gluing operator is used. It is proved that the final uniform error is of order O(h⁴ + ε), where ε is the error of the approximation of the mentioned integrals and h is the mesh step. For the p-order derivatives (p = 0,1, …) of the difference between the approximate and the exact solutions, in each “singular” part order is obtained. The method is illustrated in solving the problem in L-shaped polygon with the corner singularity. Dependence of the approximate solution and its errors on ε, h and the number of quadrature nodes n are demonstrated. Furthermore, by the constructed approximate solution on the “singular” part of the polygon, a highly accurate formula for the stress intensity factor is given.

From the error estimation formula (33) of Theorem 7 it follows that the error of the approximate solution on the block sectors decreases as , which gives an additional accuracy of the BGM near the singular points.

The method and results of this paper are valid for multiply connected polygons.

References

1 Li Z. C., Combined Methods for Elliptic Problems with Singularities, Interfaces and Infinities, 1998, Kluwer Academic Publishers, Dordrecht, The Netherlands.
10.1007/978-1-4613-3338-8
Google Scholar
2 Dosiyev A. A., The high accurate block-grid method for solving Laplace′s boundary value problem with singularities, SIAM Journal on Numerical Analysis. (2004) 42, no. 1, 153–178, https://doi.org/10.1137/S0036142900382715, MR2051061, ZBL1080.65103.
10.1137/S0036142900382715
Web of Science® Google Scholar
3 Dosiyev A. A., A block-grid method for increasing accuracy in the solution of the Laplace equa-tion on polygons, Russian Academy of Sciences. (1992) 45, no. 2, 396–399.
Google Scholar
4 Dosiyev A. A., A block-grid method of increased accuracy for solving Dirichlet′s problem forLaplace′s equation on polygons, Computational Mathematics and Mathematical Physics. (1994) 34, no. 5, 591–604.
Web of Science® Google Scholar
5 Dosiyev A. A. and Cival S., A difference-analytical method for solving Laplace′s boundary valueproblem with singularities, Proceedings of Conference Dynamical Systems and Applications, July 2004, Antalya, Turkey, 339–360.
Google Scholar
6 Dosiyev A. A. and Cival S., A combined method for solving Laplace′s boundary value problem with singularities, International Journal of Pure and Applied Mathematics. (2005) 21, no. 3, 353–367, MR2153291, ZBL1080.65104.
Google Scholar
7 Dosiyev A. A. and Buranay S. C., K. Tas, J. A. T. Machado, and D. Baleanu, A fourth order accurate difference-analytical method for solving Laplace′s boundary value problem with singularities, Mathematical Methods in Engineers, 2007, Springer, 167–176.
10.1007/978-1-4020-5678-9_13
Google Scholar
8 Dosiyev A. A., Cival Buranay S., and Subasi D., The block-grid method for solving Laplace′s equation on polygons with nonanalytic boundary conditions, Boundary Value Problems. (2010) 22, 468594, MR2671639, ZBL1214.65054.
Google Scholar
9 Dosiyev A. A., Buranay S. C., and Subasi D., The highly accurate block-grid method in solving Laplace′s equation for nonanalytic boundary condition with corner singularity, Computers & Mathematics with Applications. (2012) 64, no. 4, 616–632, https://doi.org/10.1016/j.camwa.2011.12.068, MR2948608, ZBL1252.65204.
10.1016/j.camwa.2011.12.068
Web of Science® Google Scholar
10 Volkov E. A., Approximate solution of Laplace′s equation by the block method on polygons undernonanalytic boundary conditions, Proceedings of the Steklov Institute of Mathematics. (1993) no. 4, 65–90.
Google Scholar
11 Volkov E. A., Differentiability properties of solutions of boundary value problems for the Laplaceand Poisson equations on a rectangle, Proceedings of the Steklov Institute of Mathematics. (1965) 77, 101–126.
Google Scholar
12 Samarskii A. A., The Theory of Difference Schemes, 2001, 240, Marcel Dekker, New York, NY, USA, Monographs and Textbooks in Pure and Applied Mathematics, https://doi.org/10.1201/9780203908518, MR1818323.
10.1201/9780203908518
Google Scholar
13 Dosiyev A. A., On the maximum error in the solution of Laplace equation by finite difference method, International Journal of Pure and Applied Mathematics. (2003) 7, no. 2, 229–241, MR1987130, ZBL1057.65075.
Google Scholar
14 Dosiyev A. A., A fourth order accurate composite grids method for solving Laplace′s boundary value problems with singularities, Computational Mathematics and Mathematical Physics. (2002) 42, no. 6, 867–884, MR1932812.
Google Scholar
15 Volkov E. A., An exponentially converging method for solving Laplace′s equation on polygons, Mathematics of the USSR-Sbornik. (1980) 37, no. 3, 295–325.
10.1070/SM1980v037n03ABEH001954
Web of Science® Google Scholar
16 Volkov E. A., Block Method for Solving the Laplace Equation and for Constructing Conformal Mappings, 1994, CRC Press, Boca Raton, Fla, USA, MR1412578.
Google Scholar
17 Fix G. J., Gulati S., and Wakoff G. I., On the use of singular functions with finite element approximations, Journal of Computational Physics. (1973) 13, 209–228, MR0356540, https://doi.org/10.1016/0021-9991(73)90023-5, ZBL0273.35004.
10.1016/0021-9991(73)90023-5
Web of Science® Google Scholar

All articles

A Fourth-Order Block-Grid Method for Solving Laplace′s Equation on a Staircase Polygon with Boundary Functions in C^k,λ

Abstract

1. Introduction

2. Dirichlet Problem on a Staircase Polygon

3. 9-Point Solution on Rectangles

4. System of Block-Grid Equations

5. Stress Intensity Factor

6. Numerical Results

7. Conclusions

References

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

A Fourth-Order Block-Grid Method for Solving Laplace′s Equation on a Staircase Polygon with Boundary Functions in Ck,λ

Abstract

1. Introduction

2. Dirichlet Problem on a Staircase Polygon

3. 9-Point Solution on Rectangles

4. System of Block-Grid Equations

5. Stress Intensity Factor

6. Numerical Results

7. Conclusions

References

Figures

References

Related

Information

A Fourth-Order Block-Grid Method for Solving Laplace′s Equation on a Staircase Polygon with Boundary Functions in C^k,λ