In view of the state-driven switching method, the sufficient stability conditions with delay independence will be derived for the switched large-scale time-delay systems. A new stability criterion of switched large-scale time-delay systems is deduced by Lyapunov stability theorem. The method can be applied to cases when all individual switched systems are unstable. Finally, one example is exploited to illustrate the proposed schemes.

1. Introduction

Switched systems form an important class of hybrid systems. Such systems can be described by a family of continuous-time subsystems (or discrete-time subsystems) and a rule that orchestrates the switching among them. It is well known that a wide class of physical systems in power systems, chemical procedure control systems, navigation systems, automobile speed change systems, and so forth may be appropriately described by the switched model [1–10]. In the study of switched systems, most works have been centered on the problem of stability. In the last two decades, there have been increasing interests in the stability analysis for such switched systems; see, for example, [11] and the references cited therein.

Two important methods are used to construct the switching law for the stability analysis of the switched systems. One is the state-driven switching strategy; the other is the time-driven switching strategy. The time-driven switching method is formed based on the main concept of a dwell time. If at least one stable subsystem exits, then the switched system is stable with a proper dwell time switching law. However, in reality, it is not unusual to encounter cases in which all subsystems are unstable. Therefore, [6] proposed that all subsystem can be unstable for time-driven switching method. We would have to turn to the state-driven switching strategy, from which many choices of switching laws ensuring stability exist, even if all the subsystems are unstable. Reference [5] proposed quadratic stabilizability via state feedback for both continuous-time and discrete-time switched linear systems that are composed of polytopic uncertain subsystems. For continuous-time switched linear systems, if there exists a common positive definite matrix for stability of all convex combinations of the extreme points which belong to different subsystem matrices, then the switched system is quadratically stabilizable via state feedback. The switching rules can be obtained by using the obtained common positive definite matrix.

Furthermore, the time-delay phenomenon is also unavoidable in practical systems, for instance, chemical process, long distance transmission line, hybrid procedure, electron network, and so forth. Time delays may cause instability and poor performance for practical systems [12]. In view of the aforementioned facts, the stability of switched systems with time delay is very worthy of research [13, 14]. Reference [13] studied stability and L₂ gain properties for a class of switched systems which are composed of a finite number of linear time-invariant symmetric systems with time delay and showed that, when all subsystems are in sense of satisfying an LMI, the switched system is asymptotically stable under arbitrary switching. Reference [14] proposed a delay-dependent robust H_∞ controller design method for the uncertain linear switched systems with time delay. Reference [15] investigated the problem of robust L_∞ reliable control for uncertain switched nonlinear systems with time delay and actuator failures. References [16, 17] concerned with the problem of delay-dependent stability analysis for a class of two-dimensional discrete switched systems described by the Roesser model with state delays. Besides, a large-scale system is often considered as a set of interconnected subsystems. The advantage of this aspect in stability analysis is to reduce complexity [18, 19]. Recently, many approaches have been used to investigate the stability and stabilization of large-scale time-delay systems [20, 21]. Therefore, the stability analysis of switched large-scale time-delay systems is very worthy to be researched.

Basically, current efforts to achieve stability in time-delay systems can be divided into two categories, namely, delay-independent criteria and delay-dependent criteria. For the delay-dependent criteria, the Lyapunov-Krasovskii functional technique is most suitable for application; the proposed criterion adopting this technique performs much better than several existing criteria [22–24]. In this paper, the delay-independent stability of switched large-scale time-delay system is considered. In view of the state-driven switching method, a new stability criterion of switched large-scale time-delay system is deduced by Lyapunov stability theorem [25]. This method can be applied to cases when all individual switched systems are unstable.

The following notations will be used throughout the paper: λ(A) stands for the eigenvalues of matrix A, λ_max(A) means the maximum eigenvalue in matrix A; that is, λ_max(A) = Max [λ(A)], ∥A∥ denotes the norm of matrix A; that is, ∥A∥ = Max [λ(A^TA)] ^1/2, and A^T is the transpose of matrix A.

2. System Description and Problem Statement

Consider the switched time-delay large-scale systems

()

where are the state vectors of the ith subsystem, i = 1, 2, …, N,, and B_{σ(x)_ij} are some constant matrices of compatible dimensions, , and σ(x(t)) : Rⁿ → {1, 2, …, r} is a piecewise constant function of time, called a switch signal; that is, the matrix A_{σ(x)_ii} switches between matrices A_{1_ii}, A_{2_ii}, …, A_{r_ii} belonging to the set A ≡ {A_{1_11}, A_{2_ii}, …, A_{r_ii}} and A_{l_ii} l ∈ {1, 2, …, r}. The matrix B_{σ(x)_ij} switches between matrices B_{1_ij}, B_{2_ij}, …, B_{r_ij} belonging to the set B ≡ {B_{1_ij}, B_{2_ij}, …, B_{r_ij}} and B_{l_ij}, i, j ∈ {1, 2, …, N}. A_{σ(x)_ii}, A_{σ(x)_ij}, and B_{σ(x)_ij} are matrices of compatible dimensions. τ > 0 is the time-delay duration. ψ_i(t) is a vector-valued initial continuous function defined on the interval [−τ, 0], and finally ψ_i(t), defined on −τ ≤ t ≤ 0, is the initial condition of the state, N is the number of interconnected subsystems, n is the whole systems dimension, and r is the number of individual systems.

As we have indicated, very few research articles have ever discussed the stability of the switched time-delay large-scale system (1a) and (1b). To facilitate our analysis later, some helpful lemmas are given below first.

First, we consider the normal time-delay system

()

where x ∈ Rⁿ, A and B are matrices in proper dimensions, and τ is the delay duration.

Lemma 1 (see [26].)The stability with delay independence of system (2) implies the stability with delay independence for the following systems:

()

and vice versa.

Lemma 2. There exists a switching law for the switched system (1a) and (1b) such that the system is asymptotically stable if there exist positive constants α_i (1 ≤ i ≤ N) satisfying such that the convex combination of the whole switched time-delay system

()

is an asymptotically stable system.

Proof. Since there exist positive numbers α_i (1 ≤ i ≤ N) such that is asymptotically stable, there exists a Lyapunov function V(x) such that

()

It follows that, for any t, there exists an i ∈ {1, 2, …, N} such that

()

From (6), it implies that a convex combination of the corresponding Lyapunov function is negative along the trajectory and from, at least one must be negative. Thus, switched time-delay system (1a) and (1b) is asymptotically stable.

Remark 3. Condition (6) will be used to design switching laws. The technique is that the switching is forced so that the active system is always in the region corresponding to the Lyapunov function with negative derivative.

Lemma 4. In view of Lemma 1, the stability with delay independence of implies the stability with delay independence for the following systems:

()

and vice versa.

Thus, the system (7) is an asymptotically stable system; then, the system (4) is stable. That is, the switched time-delay system (1a) and (1b) is also stable.

A sufficient condition for stability of the switched time-delay large-scale system (1a) and (1b) is established in the following theorem by using the state-switched method.

3. Stabilization Analysis of Switched Large-Scale Time-Delay System

The system (1a) and (1b) can be rewritten as the following:

()

where

()

First, we consider the switched large-scale time-delay system (1a) and (1b) with r = N = 2:

()

that is,

()

In the light of Lemma 2, it is obvious that the stability of the switched time-delay system ((10a), (10b), and (10c)) is equivalent to that of the system

()

that is,

()

To investigate the stability of system (11a) and (11b), we choose the Lyapunov function candidate as

()

where P = diag [P₁, P₂] is a unique real symmetric positive-definite matrix satisfying the Lyapunov equations:

()

It will be convenient throughout this section to use the following notations:

()

Theorem 5. Suppose the switched large-scale time-delay system (1a) and (1b) with r = N = 2. There exists a switching law such that the switched large-scale time-delay system (1a) and (1b) is asymptotically stable of delay independence, if constant and there matrices P₁, P₂ > 0 satisfying

()

Proof. The Lyapunov function for the overall system is

()

The differential of the Lyapunov function (17) is as follows:

()

By using Razumikhin theorem [27], we assume that there exists a real υ > 1 such that

()

then,

()

By continuity, there exists a υ = 1 + δ with δ > 0 sufficiently small such that

for all i. Therefore,

()

Furthermore, let α₁ = α, α₂ = 1 − α; therefore,

()

If inequalities ((16a), (16b) and, (16c)) are satisfied and constant , then . Hence, there exists a switching law such that system (1a) and (1b) is asymptotically stable.

Switching Law. Switched large-scale time-delay system ((1a), (1b)) with r = N = 2 is switched to or stay at mode i at time t if inequality (23) is satisfied at time t:

()

Furthermore, we can extend to the case of r = N switched systems. In the light of Lemma 2, it is obvious that the stability of the switched large-scale time-delay system (1a) and (1b) is equivalent to that of the system

()

To investigate the stability of system (24), we choose the Lyapunov function candidate as

()

where P = diag (P₁, P₂, …, P_N) are unique real symmetric positive-definite matrices satisfying the Lyapunov equations

()

Without loss of generality, A_{i_ii} are Hurwitz matrices.

Now, another sufficient condition for the stabilization of switched large-scale time-delay system (1a) and (1b) with r = N switched subsystems is addressed as the following theorem.

Theorem 6. Suppose the switched large-scale time-delay system (1a) and (1b) with N switched subsystems, and then there exists a switching law such that switched large-scale time-delay system (1a) and (1b) is asymptotically stable of delay independence if constants α_l satisfy

()

Proof. With the same as proof of Theorem 5, Theorem 6 can be proved.

Switching Law. The switched time-delay system (1a) and (1b) is switched to or stay at mode i at time t if inequality (28) is satisfied at time t:

()

Corollary 7. The nominal large-scale switched systems (1a) and (1b) without time-delay, that is, B_{l_ij} = 0, and then there exists a switching law such that switched large-scale system is asymptotically stable if constants α_l satisfy

()

Furthermore, we can develop another method to investigate the stability of switched large-scale time-delay systems (1a) and (1b).

In the light of Lemma 1, it is obvious that the stability of the switched time-delay system (1a) and (1b) is equivalent to that of the switched large-scale system

()

where

and

In the light of Lemma 4, a convex combination of switched large-scale systems (31) can be written as follows:

()

First, we consider the switched system (1a) and (1b) with r = N = 2. In the light of Lemma 4, it is obvious that the stability of the switched time-delay system is equivalent to that of the system

()

where 0 ≤ α ≤ 1.

To investigate the stability of system (33), we choose the Lyapunov function candidate as

()

where

and P = diag [P₁, P₂] are unique real symmetric positive-definite matrices satisfying the Lyapunov equations (14).

It will be convenient throughout the remainder of this section to use the following notations:

()

Now, another sufficient condition for the stabilization of switched large-scale time-delay system (1a) and (1b) with r = N = 2 is addressed as the following theorem.

Theorem 8. Suppose the switched time-delay system (1a) and (1b) with r = N = 2. These exists a switching law such that the switched time-delay system (1a) and (1b) is asymptotically stable of delay independence if constant and there matrices P₁, P₂ > 0 satisfying

()

Proof. The Lyapunov function for the overall system is

()

The differential of the Lyapunov function (37) is as follows

()

If inequalities ((36a), (36b), and (36c)) are satisfying and constant , then . Hence, there exists a switching law such that system (1a) and (1b) is asymptotically stable.

Switching Law. Switched time-delay system (1a) and (1b) with r = N = 2 is switched to or stay at mode i at time t if inequality (39) is satisfied at time t:

()

Now, a sufficient condition for the stabilization of switched large-scale time-delay system (1a) and (1b) with r = N switched systems is addressed as the following theorem.

Theorem 9. Suppose the switched large-scale time-delay system (1a) and (1b) with arbitrary N switched systems, and then there exists a switching law such that switched large-scale time-delay system (1a) and (1b) is asymptotically stable of delay independence if constants α_l satisfy

()

where f_{l_li} = ∥A_{l_li}∥ + ∥B_{l_li}∥, f_{j_li} = ∥A_{j_li}∥ + ∥B_{j_li}∥, f_{j_il} = ∥A_{j_il}∥ + ∥B_{j_il}∥, f_{j_lj} = ∥A_{j_lj}∥ + ∥B_{j_lj}∥, f_{l_il} = ∥A_{l_il}∥ + ∥B_{l_il}∥, and λ_max(P_i) = P_λi , i = 1, 2, …, N.

Proof. With the same as proof of Theorem 8, Theorem 9 can be proved.

Corollary 10. The nominal switched large-scale systems (1a) and (1b) without time-delay, that is, B_{l_ij} = 0, and then there exists a switching law such that switched large-scale system is asymptotically stable if constants α_l satisfy

()

Remark 11. The main contribution of the results is that this method can be applied to cases when all individual switched systems are unstable in this paper.

4. Numerical Example

Example 12. Consider a switched time-delay system composed of three individual switched systems given as follow.

Switched System 1:

()

Switched System 2:

()

Switched System 3:

()

Via normal tests of stability for the large-scale time-delay system, three individual switched systems ((42a), (42b), and (42c)) are all unstable. Furthermore, according to Lyapunov equation (26), the P_i (i = 1, 2, 3) can be obtained as the following:

()

In view of the stability conditions of Theorem 6, the conditions (27a) and (27b) can be written as follows:

()

Furthermore, let α₃ = 1 − α₁ − α₂; the above conditions ((44a), (44b), and (44c)) can be integrated as

()

Therefore, α₁ and α₂ are selected inside the admissible region of the triangle as shown in Figure 1, and the switched time-delay system ((42a), (42b), and (42c)) is asymptotically stable by the following switching law:

()

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

The admissible region α₁ and α₂ (x_label: α₁, y_label: α₂ and α₁ + α₂ + α₃ = 1).

In view of the stability conditions of Theorem 9, in addition, the conditions (40a) and (40b) can be written as follows:

()

Furthermore, let α₃ = 1 − α₁ − α₂; the above conditions ((47a), (47b), and (47c)) can be integrated as

()

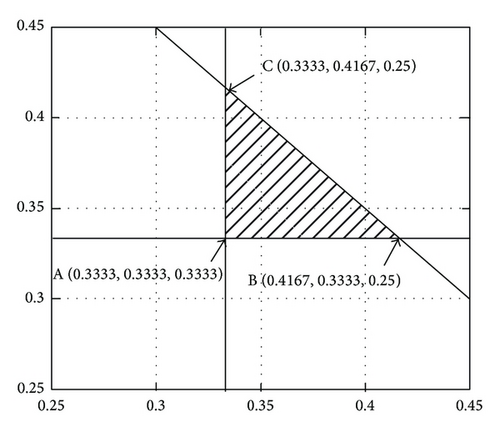
Therefore, α₁ and α₂ are selected inside the admissible region of the triangle as shown in Figure 2.

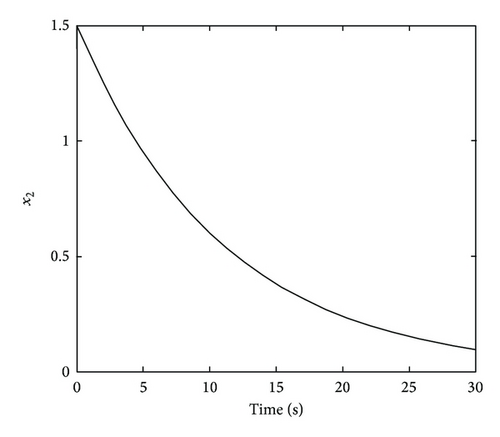
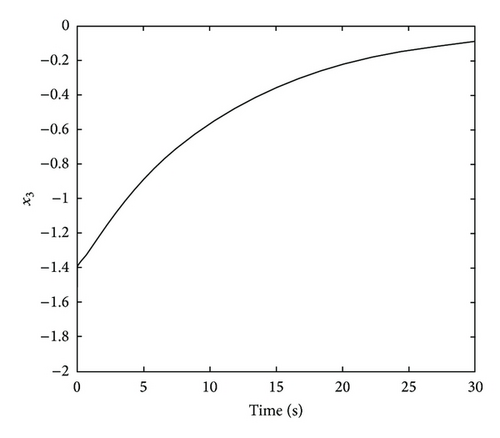
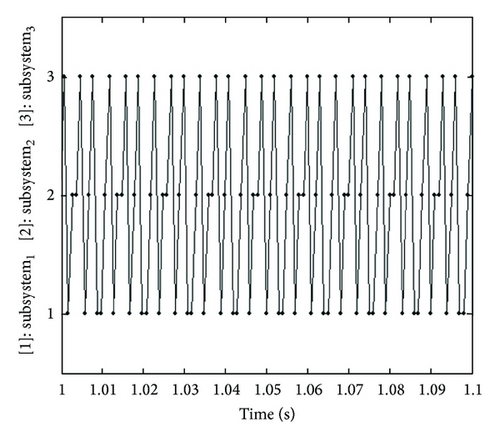
The trajectories of the switched large-scale time-delay system ((42a), (42b), and (42c)) and the switching during period [0.5, 0.6] sec are shown in Figure 3 with initial value and τ = 0.5 sec.

5. Conclusion

We have shown that the Lyapunov stability theorem can deal with the stabilization of switched large-scale time-delay systems. In addition, it is shown that the main advantages of our approach are that it can be applied to cases when all individual switched systems are unstable, quantify the region of stability, extend to arbitrary subsystems of switched large-scale time-delay systems, and develop the simple switching rule to stabilize the switched large-scale time-delay systems. For future research, we are interested in topics such as the stability problems of designing the switched laws with time dependency for the switched large-scale time-delay systems?

Acknowledgment

This work is supported by the National Science Council, Taiwan, under Grand nos. NSC 102-2221-E-218 -017 and NSC100-2632-E-218-001-MY3.

References

1 Morse A. S., Supervisory control of families of linear set-point controllers—part I: exact matching, IEEE Transactions on Automatic Control. (1996) 41, no. 10, 1413–1431, https://doi.org/10.1109/9.539424, MR1413375, ZBL0872.93009.
10.1109/9.539424
Web of Science® Google Scholar
2 Liberzon D. and Morse A. S., Basic problems in stability and design of switched systems, IEEE Control Systems Magazine. (1999) 19, no. 5, 59–70, 2-s2.0-0033311181, https://doi.org/10.1109/37.793443.
10.1109/37.793443
Web of Science® Google Scholar
3 Sun H. and Hou L., Composite disturbance observer-based control and H_∞ output tracking control for discrete-time switched systems with time-varying delay, Mathematical Problems in Engineering. (2013) 2013, 12, 698935, MR3049790.
Web of Science® Google Scholar
4 Hespanha J. P. and Morse A. S., Stability of switched systems with average dwell-time, Proceedings of the 38th IEEE Conference on Decision and Control (CDC ′99), December 1999, 2655–2660, 2-s2.0-0033314314.
Google Scholar
5 Zhai G., Lin H., and Antsaklis P. J., Quadratic stabilizability of switched linear systems with polytopic uncertainties, International Journal of Control. (2003) 76, no. 7, 747–753, https://doi.org/10.1080/0020717031000114968, MR1979895, ZBL1034.93055.
10.1080/0020717031000114968
Web of Science® Google Scholar
6 Li Z., Soh Y., and Wen C., Switched and Impulsive Systems: Analysis, Design and Application, 2005, Springer, Berlin, Germany, MR2129876.
10.1007/b100366
Google Scholar
7 Bu X., Yu F., Fu Z., and Wang F., Stability analysis of high-order iterative learning control for a class of nonlinear switched systems, Abstract and Applied Analysis. (2013) 2013, 13, 684642, MR3081572.
10.1155/2013/684642
Google Scholar
8 Huang S., Xiang Z., and Karimi H. R., Stabilization and controller design of 2D discrete switched systems with state delays under asynchronous switching, Abstract and Applied Analysis. (2013) 2013, 12, 961870, MR3055965, ZBL1271.93131.
10.1155/2013/961870
Google Scholar
9 Dombovari Z., Barton D. A. W., Eddie Wilson R., and Stepan G., On the global dynamics of chatter in the orthogonal cuttingmodel, International Journal of Non-Linear Mechanics. (2011) 46, no. 1, 330–338, 2-s2.0-78649634551, https://doi.org/10.1016/j.ijnonlinmec.2010.09.016.
10.1016/j.ijnonlinmec.2010.09.016
Web of Science® Google Scholar
10 Szalai R., Stepan G., and Hogan S. J., Global dynamics of low immersion high-speed milling, Chaos. (2004) 14, no. 4, 1069–1077, 2-s2.0-15044361103, https://doi.org/10.1063/1.1807395.
10.1063/1.1807395
PubMed Web of Science® Google Scholar
11 Wei J., Shi P., Karimi H. R., and Wang B., BIBO stability analysis for delay switched systems with nonlinear perturbation, Abstract and Applied Analysis. (2013) 2013, 8, 738653, MR3055935, ZBL1271.93134.
10.1155/2013/738653
Google Scholar
12 Zhang Y., Zhang Y., Li J., and Zhu B., Dissipative output tracking control of linear systems with time delay, Abstract and Applied Analysis. (2013) 2013, 8, 324741, MR3064404.
10.1155/2013/324741
Google Scholar
13 Zhai G., Sun Y., Chen X., and Michel A. N., Stability and L₂ gain analysis for switched symmetric systems with time delay, Proceedings of the American Control Conference, June 2003, Denver, Colo, USA, 2682–2687, 2-s2.0-0142246210.
Google Scholar
14 Shi J., Wu T., and Du S., Delay-dependent robust H_∞ control for switched systems with parameter uncertainties and time delay, Proceedings of the 5th World Congress on Intelligent Control and Automation, June 2004, Hangzhou, China, 951–955, 2-s2.0-4444275781.
Google Scholar
15 Huang S. and Xiang Z., Robust L_∞ reliable control for uncertain switched nonlinear systems with time delay under asynchronous switching, Applied Mathematics and Computation. (2013) 222, 658–670, https://doi.org/10.1016/j.amc.2013.07.084, MR3115902.
10.1016/j.amc.2013.07.084
Web of Science® Google Scholar
16 Huang S. and Xiang Z., Delay-dependent stability for discrete 2D switched systems with state delays in the roesser model, Circuits, Systems, and Signal Processing. (2013) 32, no. 6, 2821–2837, https://doi.org/10.1007/s00034-013-9600-9, MR3122256.
10.1007/s00034-013-9600-9
Web of Science® Google Scholar
17 Xiang Z. and Huang S., Stability analysis and stabilization of discrete-time 2D switched systems, Circuits, Systems, and Signal Processing. (2013) 32, no. 1, 401–414, https://doi.org/10.1007/s00034-012-9464-4, MR3018783.
10.1007/s00034-012-9464-4
Web of Science® Google Scholar
18 Yu G., Niu S., Ma J., and Song Y., An adaptive prediction-correction method for solving large-scale nonlinear systems of monotone equations with applications, Abstract and Applied Analysis. (2013) 2013, 13, 619123, MR3055929, ZBL1275.65029.
10.1155/2013/619123
Google Scholar
19 Farid M., Leong W. J., Malekmohammadi N., and Mamat M., Scaled diagonal gradient-type method with extra update for large-scale unconstrained optimization, Abstract and Applied Analysis. (2013) 2013, 5, 532041, MR3039128, ZBL06209339.
10.1155/2013/532041
Google Scholar
20 Wang C.-J. and Chiou J.-S., A stability condition with delay-dependence for a class of switched large-scale time-delay systems, Journal of Applied Mathematics. (2013) 2013, 7, 360170, MR3045422, ZBL1266.93130.
10.1155/2013/360170
Google Scholar
21 Wang C.-J. and Chiou J.-S., Stabilization analysis for the switched large-scale discrete-time systems via the state-driven switching, Discrete Dynamics in Nature and Society. (2013) 2013, 5, 630545, MR3053693, ZBL1264.93190.
10.1155/2013/630545
Web of Science® Google Scholar
22 Wu H., Li N., Wang K., Xu G., and Guo Q., Global robust stability of switched interval neural networks with discrete and distributed time-varying delays of neural type, Mathematical Problems in Engineering. (2012) 2012, 18, 361871, https://doi.org/10.1155/2012/361871, MR2837461, ZBL1264.34145.
10.1155/2012/361871
Web of Science® Google Scholar
23 Zhang G., Li T., and Fei S., Further stability criterion on delayed recurrent neural networks based on reciprocal convex technique, Mathematical Problems in Engineering. (2012) 2012, 14, 829037, https://doi.org/10.1155/2012/829037, MR2837456, ZBL1264.93193.
10.1155/2012/829037
Web of Science® Google Scholar
24 Dong Y., Mei S., and Wang X., Novel stability criteria of nonlinear uncertain systems with time-varying delay, Abstract and Applied Analysis. (2011) 2011, 16, 969674, https://doi.org/10.1155/2011/969674, MR2817275, ZBL1217.93154.
10.1155/2011/969674
Google Scholar
25 Banakar A., Lyapunov stability analysis of gradient descent-learning algorithm in network training, ISRN Applied Mathematics. (2011) 2011, 12, 145801, MR2880759, ZBL1238.93069.
10.5402/2011/145801
Google Scholar
26 Hmamed A., Further results on the robust stability of uncertain time-delay systems, International Journal of Systems Science. (1991) 22, no. 3, 605–614, https://doi.org/10.1080/00207729108910637, MR1092842, ZBL0734.93067.
10.1080/00207729108910637
Web of Science® Google Scholar
27 Hale J., Theory of Functional Differential Equations, 1977, Springer, New York, NY, USA, MR0508721.
10.1007/978-1-4612-9892-2
Web of Science® Google Scholar

Citing Literature

All articles

On Delay Independent Stabilization Analysis for a Class of Switched Large-Scale Time-Delay Systems

Abstract

1. Introduction

2. System Description and Problem Statement

3. Stabilization Analysis of Switched Large-Scale Time-Delay System

4. Numerical Example

5. Conclusion

Acknowledgment

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

On Delay Independent Stabilization Analysis for a Class of Switched Large-Scale Time-Delay Systems

Abstract

1. Introduction

2. System Description and Problem Statement

3. Stabilization Analysis of Switched Large-Scale Time-Delay System

4. Numerical Example

5. Conclusion

Acknowledgment

References

Citing Literature

Figures

References

Related

Information