Volume 2013, Issue 1 825307

Research Article

Open Access

Distributed Impulsive Consensus of the Multiagent System without Velocity Measurement

Zhi-Wei Liu,

Corresponding Author

Zhi-Wei Liu

[email protected]

School of Power and Mechanical Engineering, Wuhan University, Wuhan 430072, China whu.edu.cn

Search for more papers by this author

Hong Zhou,

Hong Zhou

School of Power and Mechanical Engineering, Wuhan University, Wuhan 430072, China whu.edu.cn

Search for more papers by this author

Zhi-Hong Guan,

Zhi-Hong Guan

College of Automation, Huazhong University of Science and Technology, Wuhan 430074, China hust.edu.cn

Search for more papers by this author

Wen-Shan Hu,

Wen-Shan Hu

School of Power and Mechanical Engineering, Wuhan University, Wuhan 430072, China whu.edu.cn

Search for more papers by this author

Li Ding,

Li Ding

School of Power and Mechanical Engineering, Wuhan University, Wuhan 430072, China whu.edu.cn

Search for more papers by this author

Wei Wang,

Wei Wang

School of Power and Mechanical Engineering, Wuhan University, Wuhan 430072, China whu.edu.cn

Search for more papers by this author

Zhi-Wei Liu,

Corresponding Author

Zhi-Wei Liu

[email protected]

School of Power and Mechanical Engineering, Wuhan University, Wuhan 430072, China whu.edu.cn

Search for more papers by this author

Hong Zhou,

Hong Zhou

School of Power and Mechanical Engineering, Wuhan University, Wuhan 430072, China whu.edu.cn

Search for more papers by this author

Zhi-Hong Guan,

Zhi-Hong Guan

College of Automation, Huazhong University of Science and Technology, Wuhan 430074, China hust.edu.cn

Search for more papers by this author

Wen-Shan Hu,

Wen-Shan Hu

School of Power and Mechanical Engineering, Wuhan University, Wuhan 430072, China whu.edu.cn

Search for more papers by this author

Li Ding,

Li Ding

School of Power and Mechanical Engineering, Wuhan University, Wuhan 430072, China whu.edu.cn

Search for more papers by this author

Wei Wang,

Wei Wang

School of Power and Mechanical Engineering, Wuhan University, Wuhan 430072, China whu.edu.cn

Search for more papers by this author

First published: 12 August 2013

https://doi.org/10.1155/2013/825307

Citations: 3

Academic Editor: Zidong Wang

Share a link

Email
Wechat
Bluesky

Abstract

This paper deals with the distributed consensus of the multiagent system. In particular, we consider the case where the velocity (second state) is unmeasurable and the communication among agents occurs at sampling instants. Based on the impulsive control theory, we propose an impulsive consensus algorithm that extends some of our previous work to account for the lack of velocity measurement. By using the stability theory of the impulsive system, some necessary and sufficient conditions are obtained to ensure the consensus of the controlled multiagent system. It is shown that the control gains, the sampled period and the eigenvalues of Laplacian matrix of communication graph play key roles in achieving consensus. Finally, a numerical simulation is provided to illustrate the effectiveness of the proposed algorithm.

1. Introduction

Recently, distributed consensus has received great interest in the control community, due to broad applications in formation [1], flocking [2, 3], synchronization in complex network [4, 5], distributed filtering [6], distributed optimization [7], and so forth. The main idea of distributed consensus is that each agent only communicates with its neighbors while the whole system of agents can converge to a common value, which by nature is a local distributed algorithm. Vicsek et al. [8] studied a simple discrete-time model of agents moving in the plane with the same speed but with different headings via simulations. The corresponding theoretical analysis was provided in [9]. Olfati-Saber and Murray presented the framework of the distributed consensus in [10], where the distributed consensus was studied in the multiagent system with fixed/switching topology and with/without delays. From then on, much progress has been made in the studies of the distributed consensus of the multiagent system in recent years [11–14]. There is a growing interest focusing on the consensus algorithms of the second-order multiagent system. Lin and Jia [15] studied the consensus problem of the multiagent system with nonuniform timedelays and dynamically changing topologies. In [16, 17], Su et al. investigated second-order consensus of the multiagent system with nonlinear dynamics and a virtual leader in a dynamic proximity network.

Due to the application of communication, the distributed consensus with sampled communication has received much attention in recent years. Many valuable algorithms have been proposed to deal with sampled communication [18–25], where distributed algorithms regulate the velocity of each agent continuously in the sampling period. On the other hand, most consensus algorithms for the multiagent system rely on the availability of the full state, only limited works [26–29] have been done when velocity information is unmeasurable.

The main contribution of this paper is to propose an impulsive consensus algorithm for the multiagent system without velocity measurements in the presence of sampled communication. The impulsive control strategy is effective when the state can be regulated instantaneously. This kind of algorithms are reasonable for many network systems. For example, in multi vrobot systems, the velocity of each robot can be changed very quickly, and the operating time of the actuator is much smaller than the sampling time. Impulsive control strategies for the multiagent system with nonlinear (linear) dynamics were considered in [30–32], where the impulsive controllers regulate all states of each agent in the system. We introduced impulsive algorithms for the multiagent system in [33–35], where only the velocity of each agent is regulated by the algorithms. In [33], some necessary and sufficient conditions are obtained for consensus/static consensus of the multiagent system. The consensus means that all the agents asymptotically tend to the zero-relative position (the agents may still change their positions) with a common velocity. The static consensus can ensure that all the agents tend to a common position. The leader-following case was studied in [35]. In [34], we proposed an impulsive consensus algorithm without velocity measurement for static consensus of multiagent system. How to achieve consensus without velocity measurement is still an open problem, which is the motivation of the study presented in this paper.

This paper is organized as follows. In Section 2, some necessary mathematical preliminaries are given, and the impulsive algorithm without using velocity information is also introduced. The main results of this paper, that is, the convergence of the proposed algorithm, are presented in Section 3. In Section 4, an illustrative numerical example is given. The concluding remarks are finally stated in Section 5.

Notation. Let ℕ and ℝ denote the natural numbers and the set of real numbers, respectively. I_n and 0_n×m are the identity matrixes of order n (or simply I if no confusion arises) and the n × m matrix with all elements equal to zero (or simply 0 if no confusion arises), respectively. ρ(A) denotes the spectral radius of squares matrix A. For γ ∈ ℂ, Re(γ) and Im (γ) are the real part and the imaginary part of γ.

2. Preliminary and Problem Formulation

The communication structure of the multiagent system is described by an undirected graph 𝒢 = (𝒱, ℰ) with a set of agents 𝒱 = {1,2, …, N} and a set of edges ℰ⊆𝒱 × 𝒱 (𝒢 has no self-loops or repeated edges). An edge {i, j} in 𝒢 means that node i can receive information from node j. 𝒩_i denotes the set of neighbors of agents i, that is, 𝒩_i = {j ∈ 𝒱∣(i, j) ∈ ℰ}. The Laplacian matrix ℒ of the graph 𝒢 is defined as

()

A directed path in a digraph 𝒢 is an ordered sequence v₁, v₂, …, v_k of agents such that any ordered pair of vertices appearing consecutively in the sequence is an edge of the digraph, that is, (v_i, v_i+1) ∈ ℰ, for any i = 1,2, …, k − 1. A directed tree is a digraph, where there exists an agent, called the root, such that any other agent of the digraph can be reached by one and only one path starting at the root. 𝒯_𝒢 = {𝒱_𝒯, ℰ_𝒯} is a directed spanning tree of 𝒢, if 𝒯_𝒢 is a directed tree and 𝒱_𝒯 = 𝒱.

We consider a multiagent system with N identical agents:

()

where i ∈ 𝒩, p_i ∈ ℝ and v_i ∈ ℝ are the position and velocity of agent i, respectively, u_i ∈ ℝ is a control input. All results in this paper still hold for p_i, v_i, u_i ∈ ℝⁿ by using the Kronecker product operations.

Definition 1. Consensus in the multiagent system (2) is said to be achieved, if, for any initial state, lim _t→∞∥p_i(t) − p_j(t)∥ = 0 and lim _t→∞∥v_i(t) − v_j(t)∥ = 0, where i, j ∈ 𝒱.

In this paper, we assume that both the absolute and relative velocities are unmeasurable, and the communication among agents occurs at sampling instants. The sampled sequence is given by , which satisfies 0 < t₁ < t₂ < ⋯ < t_k < ⋯, lim _k→∞t_k = ∞, and t_k+1 − t_k = h, where sampling period h is positive constant. The following impulsive algorithm without using any velocity information is proposed and described by the following impulsive differential equations:

()

where

, i ∈ 𝒱. We assumed that v_i(t) is left-hand continuous at t = t_k, k ∈ ℕ, and v(t) is continuous at t₀ = 0.

Remark 2. The proposed algorithm only uses sampled information of relative position (i.e. x_i(t) − x_j(t)) which is different from [26–29], where the continuous position information is required. It is also different from our previous work [34] which requires the sampled information of relative position to itself in previous sampling instant (i.e., x_i(t_k) − x_i(t_k−1)).

The following lemmas are needed in the proof of the theorem.

Lemma 3 (see [36].)Zero is a simple eigenvalue of ℒ, and all the other eigenvalues have positive real parts if and only if 𝒢 contains a spanning tree.

Define

()

From [4, 37], we can get the following lemma.

Lemma 4. Let ℒ be the Laplacian matrix of the graph 𝒢. Then the (N − 1)×(N − 1) matrix defined by satisfies . Furthermore,

()

Lemma 5 (see [29].)The complex polynomial R(z) = z² + az + b, where α ∈ ℂ and β ∈ ℂ, is Hurwitz stable if and only if Re(a) > 0 and Re(a)Im (a)Im (b) + Re²(a)Re(b) − Im ²(b) > 0.

3. Consensus in Multi-Agent System

Denote the eigenvalues of L, respectively, by λ₁, λ₂, …, λ_r, where λ₁ = 0. According to Lemma 3, λ₁ = 0 is a simple eigenvalue if 𝒢 contains a spanning tree. Note that when 𝒢 is a directed graph, λ_i, for i = 1,2, …, r, may be complex numbers.

Theorem 6. The controlled multiagent system (3) can achieve consensus if and only if the graph G contains a spanning tree and ρ(M_l) < 1, where λ_l are the nonzero eigenvalues of ℒ, l = 2, …, r,

()

Proof. Note that p_i(t) is continuous at t = t_k. From (3), one has

()

Then, one has

()

Let and ; then,

()

where A = I_N ⊗ B − ℒ ⊗ C. Let X(k + 1) = (M ⊗ I₃)Y(k + 1), where M is defined in (4). From (10), one has

()

where

is defined in (6). Then,

()

Note that

()

where b = (l₁₂, l₁₃, …, l_1N) and

()

is an invertible matrix. According to Lemma 3, λ₁ = 0 is a simple eigenvalue of ℒ if the 𝒢 contains a spanning tree (it is well known that 𝒢 contains a spanning tree which is a necessary condition for consensus). Then, do not have zero eigenvalue. This implies that the eigenvalues of are λ₂, λ₃, …, λ_r. Then, there exists a nonsingular matrix P ∈ ℝ^{(n−1)×(n−1)}, such that

()

where J = diag (J₂, J₃, …, J_r),

()

N_l is multiplicity of eigenvalue λ_l and N₂ + ⋯+N_r = N − 1.

Let , where . Then, from (12),

()

where J = diag {J₂, J₃, …, J_r}.

is asymptotically stable if and only if

. Similar to analysis in [24, 29],

is asymptotically stable if and only if z(k + 1) = (B − λ_l)z(k) is stable. Note that M_l = (B − λ_l) which immediately leads to the conclusion.

Theorem 7. The controlled multiagent system (3) achieves consensus asymptotically if and only if the communication graph 𝒢 contains a spanning tree and

()

where l = 2,3, …, r,

()

Proof. Let μ be an eigenvalue of matrix M_l. Then,

()

Let

()

It is easy to know that polynomials P_l(μ), for l = 2,3, …, r, are Schur stable if and only if ρ(M_l) < 1.

()

If β₁ − λ_iαβ₂ = 0, 1 is a root of P_l(μ) = 1. Therefore, λ_ih(β₁ − λ_iαβ₂) ≠ 0, if the consensus can be achieved. Then, the consensus can be achieved if and only if the polynomials , for l = 2, …, r, are Hurwitz stable, where

()

It is easy to check

()

if and only if (18) holds. By Lemma 5, the polynomials

, for i = 1,2, …, N, are Hurwitz stable if and only if (18) and (19) hold. The proof is thus completed.

Remark 8. According to the previous discussion, both the real and imaginary parts of the eigenvalues of the Laplacian matrix play key roles in achieving consensus. The necessary and sufficient conditions in Theorems 6 and 7 are too complicated to directly display the relationship among consensus, control gains, and sampled period.

When it comes to undirected graph, the results will be more simple.

Corollary 9. The controlled multiagent system (3) achieves consensus asymptotically if and only if the undirected communication graph 𝒢 is connected and

()

where i = 2,3, …, N.

Proof. It is well known that ℒ contains N − 1 positive real eigenvalues if 𝒢 is a connected undirected graph. Then, one has b = 0 and d = 0. From Theorem 7, (18) and (19) hold if and only if (26) is satisfied. The proof is thus completed.

Remark 10. Equation (26) is nonempty, when

()

which implies that

()

So, we can choose the control gains α and β₂ from (28) and choose β₁ from (26). Therefore, it is quite easy to find suitable control gains for any connected graph 𝒢 and sampled period h.

The following corollary will show, when the control gains are given, how to determine suitable control gains h.

Corollary 11. The controlled multiagent system (3) can achieve consensus if and only if the undirected communication graph G is connected,

()

where λ_max = max {λ₂, λ₃, …, λ_N}.

Remark 12. When β₁ > λ_iαβ₂ is not satisfied, the consensus will fail. The upper bound of sampled period increases as λ_max, α, β₁, and β₂ decrease. The sampled period h does not have the lower bound, which is different from [34].

4. Illustrative Examples

In this section, an illustrative example is given to demonstrate the correctness of the theoretical analysis. We consider the controlled multiagent system (3) with 8 agents. The communication graph is shown in Figure 1. The Laplacian matrix is

()

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Communication graph.

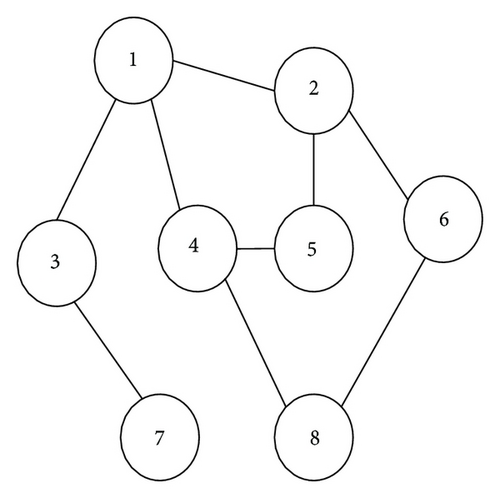
By calculation, one has λ₁ = 0, λ₂ = 0.4965, λ₃ = 1.7356, λ₄ = λ₅ = 2, λ₆ = 3.5767, λ₇ = 4, and λ₈ = 5.1912.

When the sampled period h = 1 is given, from (28), choose α = 1 and β₂ = 0.05 which satisfy

()

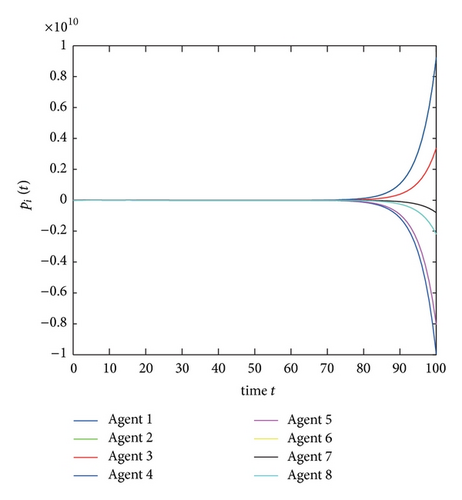
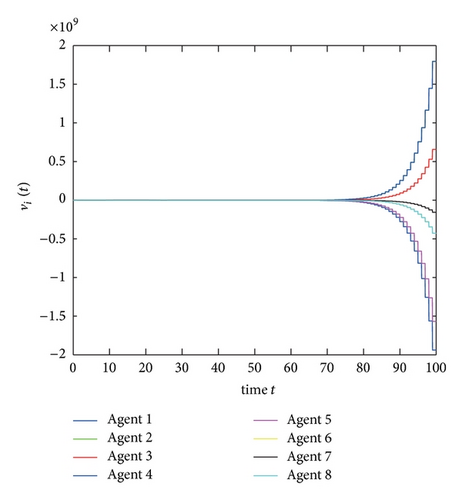
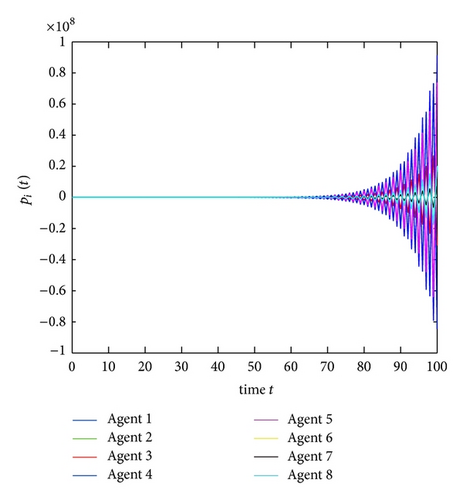
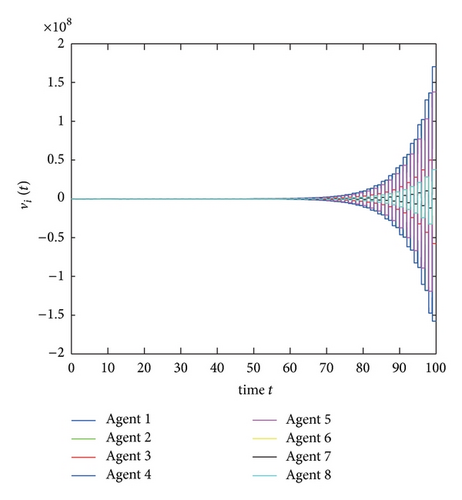
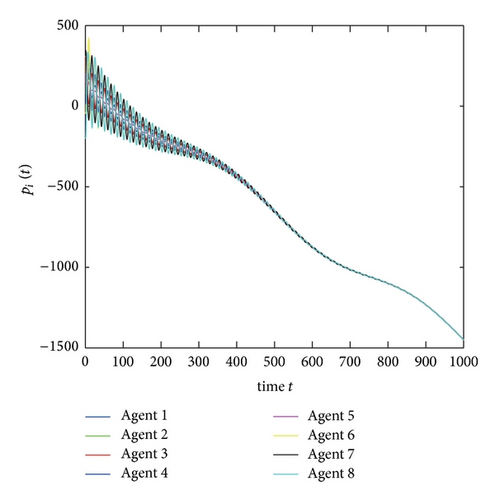
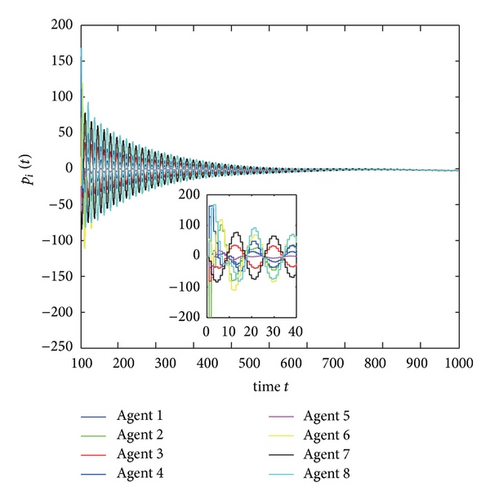
From Corollary 9, the consensus can be achieved if and only if 0.2596 < β₁ < 0.5110. Figures 2 and 3 show that consensus cannot be reached when β₁ = 0.2 and β₁ = 0.55 but can be achieved when β₁ = 0.3 (shown in Figure 4).

5. Conclusions

In this paper, the distributed consensus problem has been considered for the continuous-time multiagent system under intermittent communication. Motivated by impulsive control strategy, an impulsive consensus algorithm has been proposed, where the local algorithm of each agent is only based on the position information. Based on the stability theory of impulsive systems and the property of graph Laplacian matrix, some necessary and sufficient conditions for consensus have been obtained. From the results, we can easily find out suitable control gains for consensus. Finally, a numerical example is given to verify the theoretical analysis. It would be interesting to further investigate the multiagent system with switching topology via impulsive control to realize consensus.

Acknowledgments

This work was supported in part by the China Postdoctoral Science Foundation funded project 2012M511258 and the National Natural Science Foundation of China under Grants 61073026, 61170031, 61272069, and 61004030.

References

1 Xiao F., Wang L., Chen J., and Gao Y., Finite-time formation control for multi-agent systems, Automatica. (2009) 45, no. 11, 2605–2611, https://doi.org/10.1016/j.automatica.2009.07.012, MR2889319, ZBL1180.93006.
10.1016/j.automatica.2009.07.012
Web of Science® Google Scholar
2 Tanner H. G., Jadbabaie A., and Pappas G. J., Flocking in fixed and switching networks, IEEE Transactions on Automatic Control. (2007) 52, no. 5, 863–868, https://doi.org/10.1109/TAC.2007.895948, MR2324246.
10.1109/TAC.2007.895948
Web of Science® Google Scholar
3 Su H., Wang X., and Lin Z., Flocking of multi-agents with a virtual leader, IEEE Transactions on Automatic Control. (2009) 54, no. 2, 293–307, https://doi.org/10.1109/TAC.2008.2010897, MR2491958.
10.1109/TAC.2008.2010897
Web of Science® Google Scholar
4 Guan Z.-H., Liu Z.-W., Feng G., and Wang Y.-W., Synchronization of complex dynamical networks with time-varying delays via impulsive distributed control, IEEE Transactions on Circuits and Systems I. (2010) 57, no. 8, 2182–2195, https://doi.org/10.1109/TCSI.2009.2037848, MR2760812.
10.1109/TCSI.2009.2037848
Web of Science® Google Scholar
5 Wang Z., Wang Y., and Liu Y., Global synchronization for discrete-time stochastic complex networks with randomly occurred nonlinearities and mixed time delays, IEEE Transactions on Neural Networks. (2010) 21, no. 1, 11–25, 2-s2.0-73949136715, https://doi.org/10.1109/TNN.2009.2033599.
10.1109/TNN.2009.2033599
PubMed Web of Science® Google Scholar
6 Shen B., Wang Z., and Hung Y., Distributed H_∞-consensus filtering in sensor networks with multiple missing measurements: the finite-horizon case, Automatica. (2010) 46, no. 10, 1682–1688, https://doi.org/10.1016/j.automatica.2010.06.025, MR2877323.
10.1016/j.automatica.2010.06.025
Web of Science® Google Scholar
7 Yuan D., Xu S., and Zhao H., Distributed primal-dual subgradient method for multiagent optimization via consensus algorithms, IEEE Transactions on Systems, Man, and Cybernetics B. (2011) 41, no. 6, 1715–1724, 2-s2.0-81955161155, https://doi.org/10.1109/TSMCB.2011.2160394.
10.1109/TSMCB.2011.2160394
PubMed Web of Science® Google Scholar
8 Vicsek T., Czirók A., Ben-Jacob E., Cohen I., and Shochet O., Novel type of phase transition in a system of self-driven particles, Physical Review Letters. (1995) 75, no. 6, 1226–1229, 2-s2.0-0001730998, https://doi.org/10.1103/PhysRevLett.75.1226.
10.1103/PhysRevLett.75.1226
CAS PubMed Web of Science® Google Scholar
9 Jadbabaie A., Lin J., and Morse A. S., Coordination of groups of mobile autonomous agents using nearest neighbor rules, IEEE Transactions on Automatic Control. (2003) 48, no. 6, 988–1001, https://doi.org/10.1109/TAC.2003.812781, MR1986266.
10.1109/TAC.2003.812781
Web of Science® Google Scholar
10 Olfati-Saber R. and Murray R. M., Consensus problems in networks of agents with switching topology and time-delays, IEEE Transactions on Automatic Control. (2004) 49, no. 9, 1520–1533, https://doi.org/10.1109/TAC.2004.834113, MR2086916.
10.1109/TAC.2004.834113
Web of Science® Google Scholar
11 Cao Y., Yu W., Ren W., and Chen G., An overview of recent progress in the study of distributed multi-agent coordination, IEEE Transactions on Industrial Informatics. (2013) 9, no. 1, 427–438, https://doi.org/10.1109/TII.2012.2219061.
10.1109/TII.2012.2219061
Web of Science® Google Scholar
12 Liu Y., Ho D. W. C., and Wang Z., A new framework for consensus for discrete-time directed networks of multi-agents with distributed delays, International Journal of Control. (2012) 85, no. 11, 1755–1765, https://doi.org/10.1080/00207179.2012.703331, MR2980250, ZBL1253.93081.
10.1080/00207179.2012.703331
Web of Science® Google Scholar
13 Liu Z.-W., Guan Z.-H., Li T., Zhang X.-H., and Xiao J.-W., Quantized consensus of multi-agent systems via broadcast gossip algorithms, Asian Journal of Control. (2012) 14, no. 6, 1634–1642, https://doi.org/10.1002/asjc.525, MR3005389.
10.1002/asjc.525
Web of Science® Google Scholar
14 Olfati-Saber R., Fax J., and Murray R., Consensus and cooperation in networked multi-agent systems, Proceedings of the IEEE. (2007) 95, no. 1, 215–233, 2-s2.0-64149119332, https://doi.org/10.1109/JPROC.2006.887293.
10.1109/JPROC.2006.887293
Web of Science® Google Scholar
15 Lin P. and Jia Y., Consensus of second-order discrete-time multi-agent systems with nonuniform time-delays and dynamically changing topologies, Automatica. (2009) 45, no. 9, 2154–2158, https://doi.org/10.1016/j.automatica.2009.05.002, MR2889282, ZBL1175.93078.
10.1016/j.automatica.2009.05.002
Web of Science® Google Scholar
16 Hu Y., Su H., and Lam J., Adaptive consensus with a virtual leader of multiple agents governed by locally Lipschitz nonlinearity, International Journal of Robust and Nonlinear Control. (2013) 23, no. 9, 978–990, 2-s2.0-84859765828, https://doi.org/10.1002/rnc.2811.
10.1002/rnc.2811
Web of Science® Google Scholar
17 Su H., Chen G., Wang X., and Lin Z., Adaptive second-order consensus of networked mobile agents with nonlinear dynamics, Automatica. (2011) 47, no. 2, 368–375, https://doi.org/10.1016/j.automatica.2010.10.050, MR2878286, ZBL1207.93006.
10.1016/j.automatica.2010.10.050
Web of Science® Google Scholar
18 Gao Y. and Wang L., Sampled-data based consensus of continuous-time multi-agent systems with time-varying topology, IEEE Transactions on Automatic Control. (2011) 56, no. 5, 1226–1231, https://doi.org/10.1109/TAC.2011.2112472, MR2815935.
10.1109/TAC.2011.2112472
Web of Science® Google Scholar
19 Li T. and Zhang J., Sampled-data based average consensus with measurement noises: convergence analysis and uncertainty principle, Science in China F. (2009) 52, no. 11, 2089–2103, https://doi.org/10.1007/s11432-009-0177-7, MR2566634.
10.1007/s11432-009-0177-7
Google Scholar
20 Liu H., Xie G., and Wang L., Necessary and sufficient conditions for solving consensus problems of double-integrator dynamics via sampled control, International Journal of Robust and Nonlinear Control. (2010) 20, no. 15, 1706–1722, https://doi.org/10.1002/rnc.1543, MR2741978, ZBL1204.93080.
10.1002/rnc.1543
Web of Science® Google Scholar
21 Qin J. and Gao H., A sufficient condition for convergence of sampled-data consensus for double-integrator dynamics with nonuniform and time-varying communication delays, IEEE Transactions on Automatic Control. (2012) 57, no. 9, 2417–2422, https://doi.org/10.1109/TAC.2012.2188425, MR2968802.
10.1109/TAC.2012.2188425
Web of Science® Google Scholar
22 Qin J., Zheng W., and Gao H., Convergence analysis for multiple agents with double-integrator dynamics in a sampled-data setting, IET Control Theory & Applications. (2011) 5, no. 18, 2089–2097, https://doi.org/10.1049/iet-cta.2010.0397, MR2907774.
10.1049/iet-cta.2010.0397
Web of Science® Google Scholar
23 Qin J., Zheng W. X., and Gao H., Sampled-data consensus for multiple agents with discrete second-order dynamics, Proceedings of the 49th IEEE Conference on Decision and Control (CDC ′10), December 2010, IEEE, 1391–1396, 2-s2.0-79953133280, https://doi.org/10.1109/CDC.2010.5717420.
10.1109/CDC.2010.5717420
Google Scholar
24 Yu W., Zhou L., Yu X., Lu J., and Lu R., Consensus in multi-agent systems with second-order dynamics and sampled data, IEEE Transactions on Industrial Informatics. (2012) https://doi.org/10.1109/TII.2012.2235074.
10.1109/TII.2012.2235074
PubMed Web of Science® Google Scholar
25 Zhang Y. and Tian Y.-P., Consensus of data-sampled multi-agent systems with random communication delay and packet loss, IEEE Transactions on Automatic Control. (2010) 55, no. 4, 939–943, https://doi.org/10.1109/TAC.2010.2041612, MR2654433.
10.1109/TAC.2010.2041612
Web of Science® Google Scholar
26 Abdessameud A. and Tayebi A., On consensus algorithms for double-integrator dynamics without velocity measurements and with input constraints, Systems & Control Letters. (2010) 59, no. 12, 812–821, https://doi.org/10.1016/j.sysconle.2010.06.019, MR2779794, ZBL1217.93009.
10.1016/j.sysconle.2010.06.019
Web of Science® Google Scholar
27 Cao Y. and Ren W., Distributed coordinated tracking with reduced interaction via a variable structure approach, IEEE Transactions on Automatic Control. (2012) 57, no. 1, 33–48, https://doi.org/10.1109/TAC.2011.2146830, MR2917646.
10.1109/TAC.2011.2146830
Web of Science® Google Scholar
28 Hong Y., Hu J., and Gao L., Tracking control for multi-agent consensus with an active leader and variable topology, Automatica. (2006) 42, no. 7, 1177–1182, https://doi.org/10.1016/j.automatica.2006.02.013, MR2230987, ZBL1117.93300.
10.1016/j.automatica.2006.02.013
Web of Science® Google Scholar
29 Yu W., Zheng W. X., Chen G., Ren W., and Cao J., Second-order consensus in multi-agent dynamical systems with sampled position data, Automatica. (2011) 47, no. 7, 1496–1503, https://doi.org/10.1016/j.automatica.2011.02.027, MR2889249, ZBL1220.93005.
10.1016/j.automatica.2011.02.027
Web of Science® Google Scholar
30 Jiang H., Bi Q., and Zheng S., Impulsive consensus in directed networks of identical nonlinear oscillators with switching topologies, Communications in Nonlinear Science and Numerical Simulation. (2012) 17, no. 1, 378–387, https://doi.org/10.1016/j.cnsns.2011.04.030, MR2826016, ZBL1239.93004.
10.1016/j.cnsns.2011.04.030
Web of Science® Google Scholar
31 Liu B. and Hill D. J., Impulsive consensus for complex dynamical networks with nonidentical nodes and coupling time-delays, SIAM Journal on Control and Optimization. (2011) 49, no. 2, 315–338, https://doi.org/10.1137/080722060, MR2784690, ZBL1217.93078.
10.1137/080722060
CAS Web of Science® Google Scholar
32 Wu Q., Zhou J., and Xiang L., Impulsive consensus seeking in directed networks of multi-agent systems with communication time delays, International Journal of Systems Science. (2012) 43, no. 8, 1479–1491, https://doi.org/10.1080/00207721.2010.547630, MR2946983.
10.1080/00207721.2010.547630
Web of Science® Google Scholar
33 Guan Z.-H., Liu Z.-W., Feng G., and Jian M., Impulsive consensus algorithms for second-order multi-agent networks with sampled information, Automatica. (2012) 48, no. 7, 1397–1404, https://doi.org/10.1016/j.automatica.2012.05.005, MR2942329, ZBL1246.93007.
10.1016/j.automatica.2012.05.005
Web of Science® Google Scholar
34 Liu Z.-W., Guan Z.-H., Shen X., and Feng G., Consensus of multi-agent networks with aperiodic sampled communication via impulsive algorithms using position-only measurements, IEEE Transactions on Automatic Control. (2012) 57, no. 10, 2639–2643, https://doi.org/10.1109/TAC.2012.2214451, MR2991667.
10.1109/TAC.2012.2214451
Web of Science® Google Scholar
35 Liu Z.-W., Guan Z.-H., and Zhou H., Impulsive consensus for leader-following multiagent systems with fixed and switching topology, Mathematical Problems in Engineering. (2013) 2013, 10, https://doi.org/10.1155/2013/762861, 762861.
10.1155/2013/762861
Web of Science® Google Scholar
36 Bullo F., Cortés J., and Martinez S., Distributed Control of Robotic Networks: A Mathematical Approach to Motion Coordination Algorithms, 2009, Princeton University Press, MR2524493.
10.1515/9781400831470
Google Scholar
37 Wu C. W. and Chua L. O., Synchronization in an array of linearly coupled dynamical systems, IEEE Transactions on Circuits and Systems I. (1995) 42, no. 8, 430–447, https://doi.org/10.1109/81.404047, MR1351879, ZBL0867.93042.
10.1109/81.404047
Web of Science® Google Scholar

Citing Literature

All articles

Distributed Impulsive Consensus of the Multiagent System without Velocity Measurement

Abstract

1. Introduction

2. Preliminary and Problem Formulation

3. Consensus in Multi-Agent System

4. Illustrative Examples

5. Conclusions

Acknowledgments

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Distributed Impulsive Consensus of the Multiagent System without Velocity Measurement

Abstract

1. Introduction

2. Preliminary and Problem Formulation

3. Consensus in Multi-Agent System

4. Illustrative Examples

5. Conclusions

Acknowledgments

References

Citing Literature

Figures

References

Related

Information