Robust Synchronization Criterion for Coupled Stochastic Discrete-Time Neural Networks with Interval Time-Varying Delays, Leakage Delay, and Parameter Uncertainties
Abstract
The purpose of this paper is to investigate a delay-dependent robust synchronization analysis for coupled stochastic discrete-time neural networks with interval time-varying delays in networks coupling, a time delay in leakage term, and parameter uncertainties. Based on the Lyapunov method, a new delay-dependent criterion for the synchronization of the networks is derived in terms of linear matrix inequalities (LMIs) by constructing a suitable Lyapunov-Krasovskii’s functional and utilizing Finsler’s lemma without free-weighting matrices. Two numerical examples are given to illustrate the effectiveness of the proposed methods.
1. Introduction
In recent years, the problem of synchronization of coupled neural networks which is one of hot research fields of complex networks has been a challenging issue due to its potential applications such as physics, information sciences, biological systems, and so on. Here, complex networks, which are a set of interconnected nodes with specific dynamics, have been studied from various fields of science and engineering such as the World Wide Web, social networks, electrical power grids, global economic markets, and so on. Many mathematical models were proposed to describe various complex networks [1, 2]. Also, in the real applications of systems, there exists naturally time delay due to the finite information processing speed and the finite switching speed of amplifiers. It is well known that time delay often causes undesirable dynamic behaviors such as performance degradation and instability of the systems. So, some sufficient conditions for synchronization of coupled neural networks with time delay have been proposed in [3–5]. Moreover, the synchronization of delayed systems was applied in practical systems such as secure communication [6]. Furthermore, these days, most systems use digital computers (usually microprocessor or microcontrollers) with the necessary input/output hardware to implement the systems. The fundamental character of the digital computer is that it takes compute answers at discrete steps. Therefore, discrete-time modeling with time delay plays an important role in many fields of science and engineering applications. In this regard, various approaches to synchronization stability criterion for discrete-time complex networks with time delay have been investigated in the literature [7–9].
On the other hand, in implementation of many practical systems such as aircraft, chemical and biological systems, and electric circuits, there exist occasionally stochastic perturbations. It is not less important than the time delay as a considerable factor affecting dynamics in the fields of science and engineering applications. Therefore, the study on the problems for various forms of stochastic systems with time-delay has been addressed. For more details, see the literature [10–13] and references therein. Furthermore, on the problem of synchronization of coupled stochastic neural networks with time delay, various researches have been conducted [14–17]. Li and Yue [14] studied the synchronization stability problem for a class of complex networks with Markovian jumping parameters and mixed time delays. The model considered in [14] has stochastic coupling terms and stochastic disturbances to reflect more realistic dynamical behaviors of the complex networks that are affected by noisy environment. In [15], by utilizing novel Lyapunov-Krasovskii′s functional with both lower and upper delay bounds, the synchronization criteria for coupled stochastic discrete-time neural networks with mixed delays were presented. Tang and Fang [16] derived several sufficient conditions for the synchronization of delayed stochastically coupled fuzzy cellular neural networks with mixed delays and uncertain hybrid coupling based on adaptive control technique and some stochastic analysis methods. In [17], by using Kronecker product as an effective tool, robust synchronization problem of coupled stochastic discrete-time neural networks with time-varying delay was investigated. Moreover, Song [18–20] addressed synchronization problem for the array of asymmetric, chaotic, and coupled connected neural networks with time-varying delay or nonlinear coupling. Also, in [21], robust exponential stability analysis of uncertain delayed neural networks with stochastic perturbation and impulse effects was investigated.
Very recently, a time delay in leakage term of the systems is being put to use in the problem of stability for neural networks as a considerable factor affecting dynamics for the worse in the systems [22, 23]. Li et al. [22] studied the existence and uniqueness of the equilibrium point of recurrent neural networks with time delays in the leakage term. By use of the topological degree theory, delay-dependent stability conditions of neural networks of neutral type with time delays in the leakage term were proposed in [23]. Unfortunately, to the best of authors’ knowledge, delay-dependent synchronization analysis of coupled stochastic discrete-time neural networks with time-varying delay in network coupling and leakage delay has not been investigated yet. Thus, by attempting the synchronization analysis for the model of coupled stochastic discrete-time neural networks with time delay in the leakage term, the model for coupled neural networks and its applications are closed to the practical networks. Here, delay-dependent analysis has been paid more attention than delay-independent one because the sufficient conditions for delay-dependent analysis make use of the information on the size of time delay [24]. That is, the former is generally less conservative than the latter.
Motivated by the above discussions, the problem of a new delay-dependent robust synchronization criterion for coupled stochastic discrete-time neural networks with interval time-varying delays in network coupling, the time delay in leakage term, and parameter uncertainties is considered for the first time. The coupled stochastic discrete-time neural networks are represented as a simple mathematical model by the use of Kronecker product technique. Then, by construction of a suitable Lyapunov-Krasovskii′s functional and utilization of Finsler’s lemma without free-weighting matrices, a new synchronization criterion is derived in terms of LMIs. The LMIs can be formulated as convex optimization algorithms which are amenable to computer solution [25]. In order to utilize Finsler’s lemma as a tool of getting less conservative synchronization criteria on the number of decision variables, it should be noted that a new zero equality from the constructed mathematical model is devised. The concept of scaling transformation matrix will be utilized in deriving zero equality of the method. In [26], the effectiveness of Finsler’s lemma was illustrated by the improved passivity criteria of uncertain neural networks with time-varying delays. Finally, two numerical examples are included to show the effectiveness of the proposed method.
Notation. ℝn is the n-dimensional Euclidean space, and ℝm×n denotes the set of all m × n real matrices. For symmetric matrices X and Y, X > Y (resp., X ≥ Y) means that the matrix X − Y is positive definite (resp., nonnegative). X⊥ denotes a basis for the null-space of X. In and 0n and 0m×n denote n × n identity matrix and n × n and m × n zero matrices, respectively. ∥·∥ refers to the Euclidean vector norm or the induced matrix norm. λmax (·) means the maximum eigenvalue of a given square matrix. diag {⋯} denotes the block diagonal matrix. ⋆ represents the elements below the main diagonal of a symmetric matrix. Let (Ω, ℱ, {Ft} t≥0, 𝒫) be complete probability space with a filtration {Ft} t≥0 satisfying the usual conditions (i.e., it is right continuous and ℱ0 contains all 𝒫-pull sets). 𝔼{·} stands for the mathematical expectation operator with respect to the given probability measure 𝒫.
2. Problem Statements
Remark 1. According to the graph theory [27], the outer-coupling matrix G is called the negative Laplacian matrix of undirected graph. A physical meaning of the matrix G is the bilateral connection between node i and j. If the matrix G cannot satisfy symmetric, the unidirectional connection between nodes i and j is expressed. At this time, the matrix G is called the negative Laplacian matrix of directed graph. Therefore, new numerical model and strong sufficient condition guaranteed to the stability for networks are needed. Moreover, in order to analyze the consensus problem for multiagent systems, the Laplacian matrix of directed graph was used [28].
For the convenience of stability analysis for the network (8), the following Kronecker product and its properties are used.
Lemma 2 (see [29].)Let ⊗ denote the notation of Kronecker product. Then, the following properties of Kronecker product are easily established:
- (i)
(αA) ⊗ B = A ⊗ (αB),
- (ii)
(A + B) ⊗ C = A ⊗ C + B ⊗ C,
- (iii)
(A ⊗ B)(C ⊗ D) = (AC)⊗(BD),
- (iv)
(A ⊗ B) T = AT ⊗ BT.
The aim of this paper is to investigate the delay-dependent synchronization stability analysis of the network (14) with interval time-varying delays in network coupling, leakage delay, and parameter uncertainties. In order to do this, the following definition and lemmas are needed.
Definition 3 (see [7].)The network (8) is said to be asymptotically synchronized if the following condition holds:
Lemma 4 (see [3].)Let U = [uij] N×N, P ∈ ℝn×n, xT = [x1, x2, …, xn] T, and yT = [y1, y2, …, yn] T. If U = UT and each row sum of U is zero, then
Lemma 5 (see [30].)For any constant matrix 0 < M = MT ∈ ℝn×n, integers hm and hM satisfying 1 ≤ hm ≤ hM, and vector function x(k) ∈ ℝn, the following inequality holds:
Lemma 6 (see [31] Finsler′s lemma.)Let ζ ∈ ℝn, Φ = ΦT ∈ ℝn×n, and Υ ∈ ℝm×n such that rank(Υ) < n. The following statements are equivalent:
- (i)
ζTΦζ < 0, ∀Υζ = 0, ζ ≠ 0,
- (ii)
.
3. Main Results
Then, the main result of this paper is presented as follows.
Theorem 7. For given positive integers hm, hM and τ, diagonal matrices and , the network (14) is asymptotically synchronized for hm ≤ h(k) ≤ hM, if there exist positive scalars ρ, ϵ, positive definite matrices P, Q1, Q2, R1, R2, S1, S2, positive diagonal matrices D1, D2, and any matrix T satisfying the following LMIs for 1 ≤ i < j ≤ N:
Proof. Define a matrix U as
Also, by Theorem 7 in [32], the following inequality for any matrix T holds
Remark 8. In order to induce a new zero equality (40), the matrix Λ in (41) was defined. It is inspired by the concept of scaling transformation matrix. To reduce the decision variable, Finsler’s lemma (ii) without free-weighting matrices was used. At this time, a zero equality is required. If the matrix Λ is not considered, then the following description (see only (43) as an example)
Remark 9. In this paper, the problem of new delay-dependent synchronization for coupled stochastic discrete-time neural networks with leakage delay and parameter uncertainties is considered. By using Finsler′s lemma without free-weighting matrices, the proposed robust synchronization criterion for the network is established in terms of LMIs. Here, as mentioned in the Introduction, the leakage delay is the time delay in leakage or forgetting term of the systems and a considerable factor affecting dynamics for the worse in the network. The effect of the leakage delay which cannot be negligible is shown in Figure 2. Also, the stochastic discrete-time systems with parameter uncertainties do not formulate like as the network (14) in any other literature. To do this, the vector (η(k) − x(k)) is added in the augmented vector ζ(k). It is just like as in continuous-time systems. This form for the systems may give more less conservative results for stability analysis. As a case of stochastic continuous-time systems with parameter uncertainties, Kwon [13] derived the delay-dependent stability criteria for uncertain stochastic dynamic systems with time-varying delays via the Lyapunov-Krasovskii′s functional approach with two delay fraction numbers.
4. Numerical Examples
In this section, we provide two numerical examples to illustrate the effectiveness of the proposed synchronization criterion in this paper.
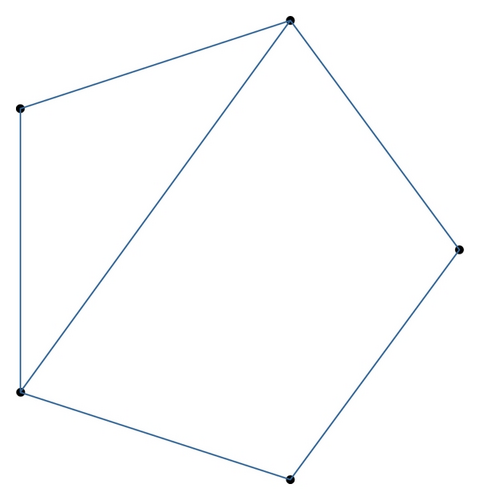
Example 10. Consider the following coupled neural networks by complex model in Figure 1:
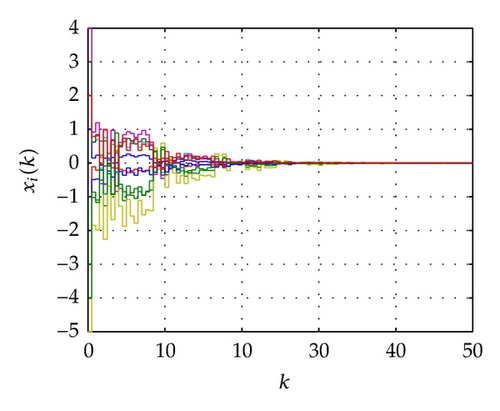
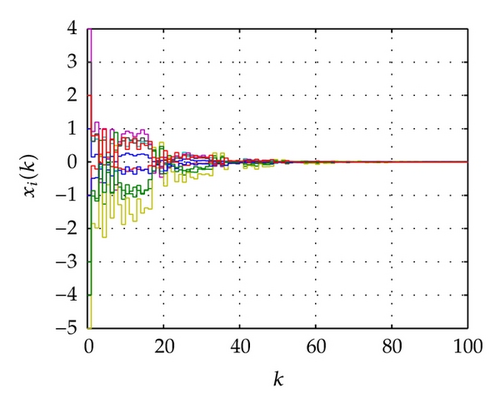
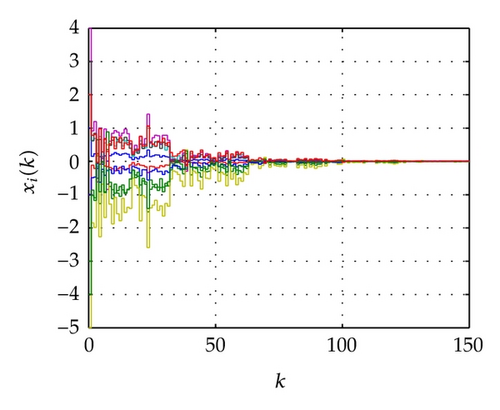
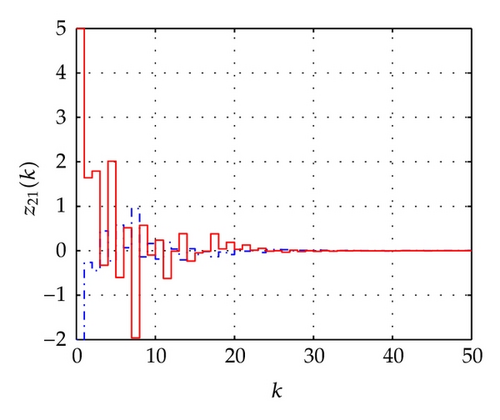
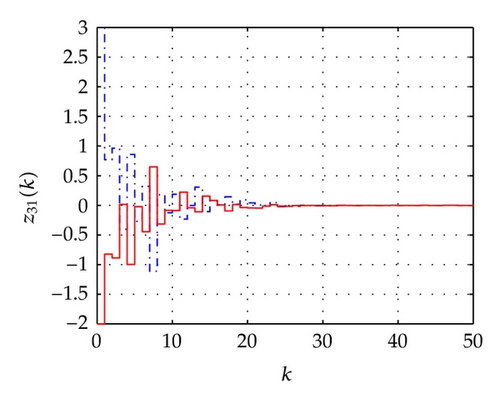
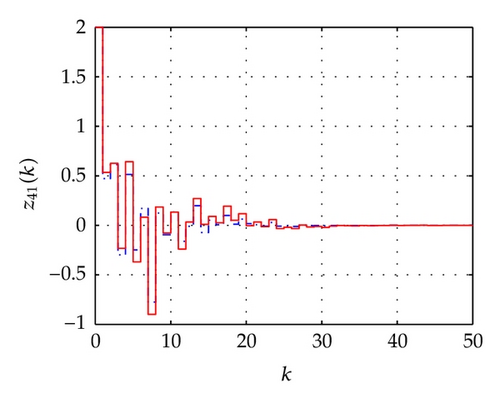
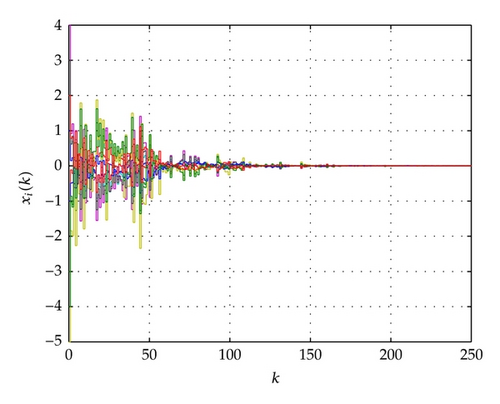
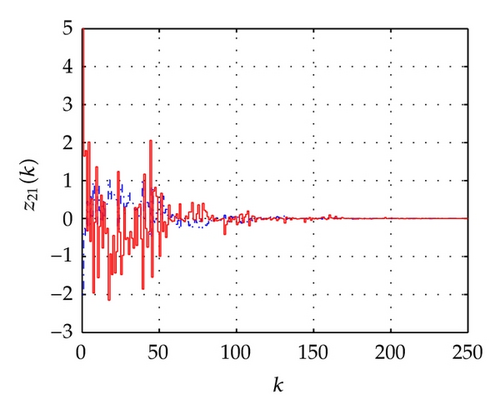
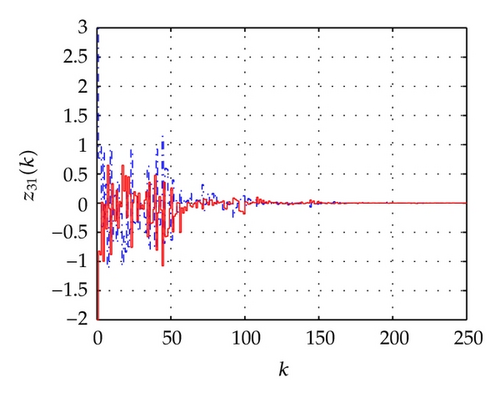
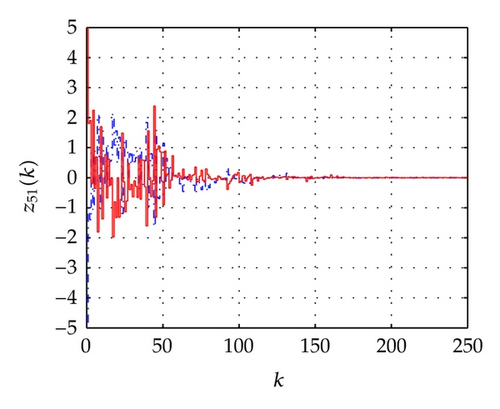
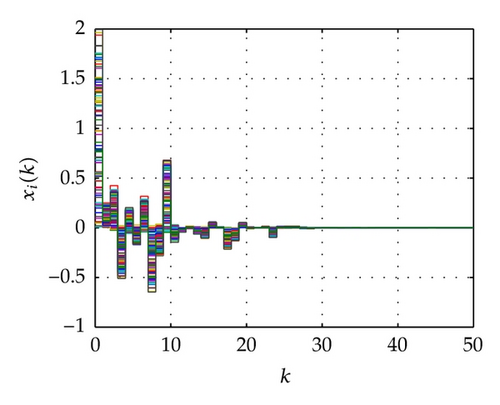
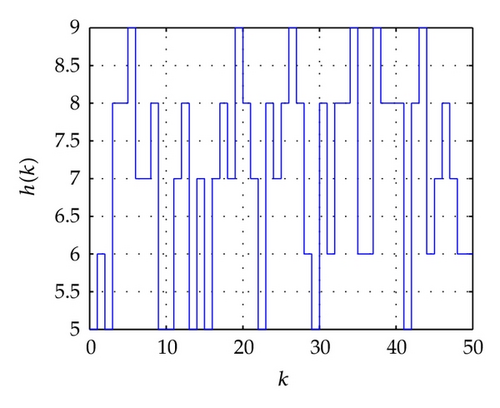
For the network above, the maximum allowable delay bounds with different hm and fixed τ = 3 by Theorem 7 are listed in Table 1. In order to confirm the obtained results with the conditions of the time delays as listed in Table 2, the simulation results for the trajectories of state responses, xi(k) (i = 2,3, 4,5), and synchronization errors, zi1(k) = xi(k) − x1(k), of the network (54) are shown in Figures 2, 3, 4, and 5. These figures show that the network with the errors converge to zero for given initial values of the state by , , , , and . Specially, the simulation results in Figure 2 show state response trajectories for the values of leakage delay, τ, by 3, 15, and 30 with fixed values hm = 5 and hM = 7. It is easy to illustrate that the larger value of leakage delay gives the worse dynamic behaviors of the network (54).
| hm | 1 | 5 | 10 | 50 | 100 |
|---|---|---|---|---|---|
| hM | 3 | 7 | 12 | 52 | 102 |
| Number | τ | hm | hM | h(k) |
|---|---|---|---|---|
| 3 | ||||
| C1-1 | 15 | 5 | 7 | sin (kπ/2) + 6 |
| 30 | ||||
| C1-2 | 3 | 50 | 52 | sin (kπ/2) + 51 |


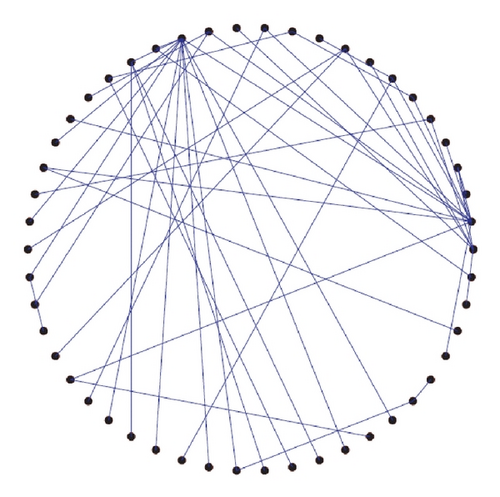
Example 11. Consider the following coupled neural networks by BA scale-free model [33] in Figure 6:
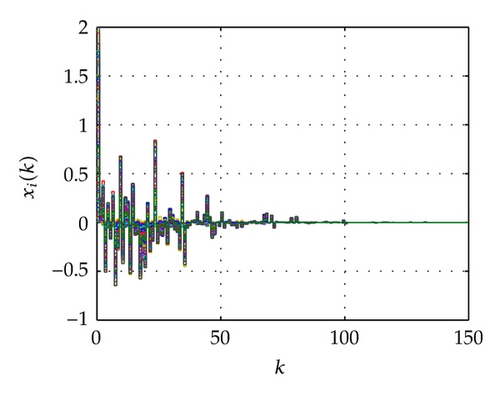
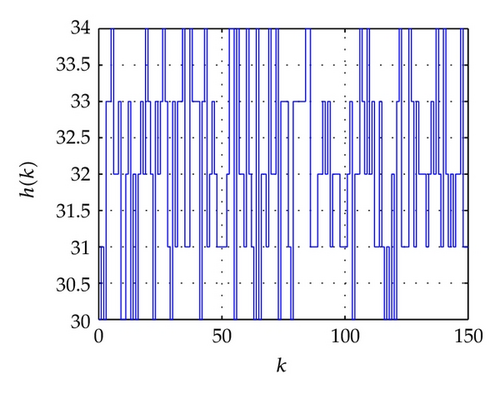
The results of maximum allowable delay bounds with different hm and fixed τ = 3 by Theorem 7 are listed in Table 3. For lack of space, the outer-coupling matrix G is omitted. It is easy that the matrix G was expressed from Figure 6. Figures 7 and 8 show the state response trajectories, xi(t) (i = 1, …, 50), of the network (56) with the condition of the time delays as listed in Table 4 for random initial values of the state. These figures show that the network (56) with the state responses converge to zero. This means the synchronization stability of the network (56).
| hm | 1 | 5 | 10 | 25 | 30 |
|---|---|---|---|---|---|
| hM | 5 | 9 | 14 | 29 | 34 |
| Number | hm | hM | h(k) |
|---|---|---|---|
| C2-1 | 5 | 9 | Random integer variable with 5 ≤ h(k) ≤ 9 |
| C2-2 | 30 | 34 | Random integer variable with 30 ≤ h(k) ≤ 34 |
5. Conclusions
In this paper, the delay-dependent robust synchronization criterion for the coupled stochastic discrete-time neural networks with interval time-varying delays in network coupling, leakage delay, and parameter uncertainties has been proposed. To do this, the suitable Lyapunov-Krasovskii’s functional was used to investigate the feasible region of stability criterion. By utilization of Finsler’s lemma with a new zero equality, a sufficient condition for guaranteeing asymptotic synchronization for the concerned networks has been derived in terms of LMIs. Two numerical examples have been given to show the effectiveness and usefulness of the presented criterion.
Acknowledgments
This research was supported by Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Education, Science and Technology (2012-0000479) and by a Grant of the Korea Healthcare Technology R & D Project, Ministry of Health & Welfare, Republic of Korea (A100054).




