A mathematical model of modified enzyme-membrane electrode for steady-state condition is discussed. This model contains a nonlinear term related to enzyme kinetics reaction mechanism. The thickness dependence of an amperometric biosensor is presented both analytically and numerically where the biological layer is immobilized between a solid substrate and permeable electrode. The analytical expressions pertaining to the concentration of species and normalized current are obtained using the Adomian decomposition method (ADM). Simple and approximate polynomial expressions of concentrations of an oxidized mediator, substrate, and reduced mediator are derived for all possible values of parameters (Thiele modulus), B_O (normalized surface concentration of oxidized mediator), and B_S (normalized surface concentration of substrate). A comparison of the analytical approximation and numerical simulation is also presented. A good agreement between theoretical predictions and numerical results is observed.

1. Introduction

In recent years, polymer membranes are widely used as carriers for immobilization of enzymes [1]. They have been utilized in biomaterials, bioseparators, and biosensors [2]. The membranes provide an ideal support for the immobilization of the biocatalyst. Substrate partition at the membrane/fluid interphase can be used to improve the selectivity of the catalytic reaction towards the desired products [3]. Recently a new method for enzyme immobilization [4], based on a molecular recognition process, has been successfully used for the building of enzymatic biosensors and also of a chemically active membrane [5]. In the recent three decades, much effort has been devoted to the development of various biosensors involving biologically sensitive component and transformers—devices with many fields of applications [6]. Changes in membrane chemistry have been demonstrated by Robeson [7]. The better way of changing the membrane geometry aims to increase the membrane area per volume, thereby speeding the separation. This increased surface area has recently been identified as a high priority research need for membranes [8].

A two-substrate model for enzyme electrode has been devised experimentally [10, 11] where the nonlinear enzyme reaction was taken into account. This model was employed to describe the behaviour of a glucose oxidize (GOx) electrode [12, 13]. It has been found that the mediators could not totally replace the natural cosubstrate when both were present in the assay solution so that here a three-substrate model would be required. In these cases, a complex calibration curve of the enzyme electrode was observed [14, 15].

Inspite of extensive experimental investigations for the design of bio-sensor, only a few studies concerned the modeling or theoretical design of such system. Recently Loghambal and Rajendran [16] have described the theoretical model in an amperometric oxidase enzyme-membrane electrode. Numerical solutions [9, 17, 18] were reported to a novel enzyme electrode. In those papers the enzyme electrode was modeled numerically using shooting method [9, 18] and Runge-Kutta method [17]. But, in this paper, the same system is modeled analytically. However, to the best of our knowledge, till date no general analytical results for the concentration of oxidized mediator, substrate, and reduced mediator for all values of the parameters , B_O, and B_S have been reported [9]. The purpose of this communication is to derive the closed-form of analytical expressions [19, 20] of concentrations of substrate and oxidized and reduced mediator by solving the system of nonlinear reaction-diffusion equations using the Adomian decomposition method (ADM) [21]. The theoretical models of enzyme electrodes give information about the mechanism and kinetics operating in the biosensor. Thus, the information gained from this modeling can be useful in sensor design, optimization, and prediction of the electrode’s response.

2. Mathematical Formulation and Analysis of the Problems

2.1. Mathematical Formulation

Building upon earlier work for these mechanisms, Gooding and Hall [9] presented a concise discussion and derivation of the dimensionless nonlinear mass transport equation for this model, which is summarized briefly for completeness. In the enzyme-membrane geometry, the biological layer is located between a solid substrate and an outer permeable electrode in contact with the sample. In this model the substrate and cosubstrate penetrate through a permeable electrode to the enzyme layer and then reduce to the form of cosubstrate which diffuses back to the electrode. The general reaction scheme for an immobilized oxidase in the presence of two oxidants can be written as follows [9]:

()

where k_m is the rate constant for the forward direction of the mth reaction and k₋₁ is the rate constant for the backward direction. If [E_T] is the total enzyme concentration in the matrix, then at all times

()

where [E_OX], [ES], and [E_red] are the oxidized mediator, enzyme-substrate complex, and reduced mediator enzyme concentrations, respectively. At steady state, the diffusion of a substrate into the enzyme layer is equal to the reaction rate of the substrate within the matrix. We examine a planar matrix of thickness y = d, where diffusion is considered in the y-direction only (edge effects are neglected) (Figure 1). The corresponding governing equations in Cartesian coordinates, for the planar diffusion and reaction in the enzyme electrode, are [9]

()

where D_M is the diffusion coefficient of the oxidized and reduced forms of the mediator (assumed to be equal) and D_S is the diffusion coefficient of substrate within the enzyme layer. [Med_OX], [Med_red], and [S] are the concentration of oxidized mediator, reduced mediator, and substrate at any position in the enzyme layer. β_S and β_O are the dimensionless rate constants (β_S = (k₋₁ + k₂)/k₁ and β_O = k₂/k₄). Equations (5a)–(5c) are solved for the following boundary conditions.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Schematic representation of a typical enzyme-membrane electrode geometry [9].

At the far wall, y = 0

()

and, at the electrode, y = d

()

The first boundary condition states that there is no flux of reactants and products at the far wall of the sensor. The second condition states that the substrates in the matrix are in equilibrium with the surrounding fluid at the surface of the electrode and all the hydrogen peroxide which reaches the electrode surface is oxidized. [Med_OX] _b and [S] _b are the concentration of oxidized mediator and substrate at the enzyme layer|electrode boundary, and [Med_OX] _∞ and [S] _∞ are the bulk solution concentrations. K_O and K_S are the equilibrium partition coefficients for oxidized mediator and the substrate, respectively.

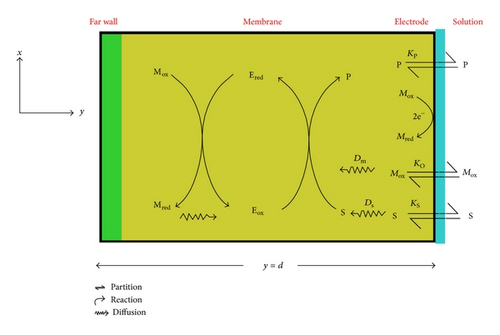
2.2. Normalized Form

We make the nonlinear differential Equations (5a)–(5c) to dimensionless form by defining the following dimensionless variables:

()

where F_O, F_S, and F_R are the normalized concentration of oxidized mediator, substrate, and reduced mediator in the matrix, respectively, and χ is the normalized distance. B_O and B_S are the normalized surface concentration of oxidized mediator and substrate.

is the Thiele modulus for the oxidized mediator which governs reaction/diffusion.

The resultant expressions for the oxidized mediator, substrate, and reduced mediator in nondimensionalized form become as follows:

()

The consumption of oxidized mediator, the consumption of substrate, and the consumption of reduced mediator are all related processes. So there is only one independent variable for which to solve

()

The normalized boundary conditions are given by

()

From (9d), we get

()

Integrating (11) and (12) twice and applying the appropriate boundary conditions (10), we get

()

Substituting (13) into (9a) and rearranging, we get

()

The normalized current response is given by the following expression:

()

3. Concentrations of Oxidized Mediator, Substrate, and Reduced Mediator under Steady-State Condition

3.1. Analytical Solution Using ADM

In this paper, the Adomian decomposition method (see Appendix A) is used to solve nonlinear differential equations. The ADM [21–25] yields, without linearization, perturbation, or transformation, an analytical solution in terms of a rapidly convergent infinite power series with easily computable terms. The basic principle of this method is described in Appendix A and detailed derivation of dimensionless concentration of oxidized mediator F_O(χ), from the nonlinear equation (15), is described in Appendix B. The analytical expression of concentration (see Appendix B) of the oxidized mediator is as follows:

()

where

Using (17) (or the dimensionless concentration F_O(χ)), we can obtain the concentrations of substrate and reduced mediator from (13) and (14). From (14), (16), and (17) we get the dimensionless current

()

3.2. Numerical Simulation

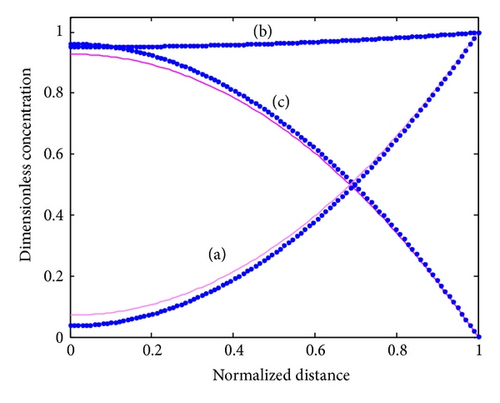
The nonlinear diffusion equations ((9a)–(9c)) for the boundary condition (10) are also solved numerically. We have used the function pdex4 in Scilab/Matlab numerical software to solve numerically the initial-boundary value problems for parabolic-elliptic partial differential equations. This numerical solution is compared with our analytical results in Figures 2 and 3 and Table 1. The average relative error between our analytical result (17) and the numerical result of oxidized mediator concentration F_O is less than 0.3% for various values of . The normalized current I is compared with simulation result in Table 3 for various values of parameters . The average relative error is less than 3%. From the table it is also inferred that the value of the current increases when the thickness of the membrane increases.

Table 1. Comparison of normalized analytical steady-state concentrations of oxidized mediator F_O (17) with the numerical results when B_O = 0.1, B_S = 0.01, and μ_S = 0.05 and for various values of

χ
	(d = 0.7878 μM)			(d = 7.878 μM)			(d = 39.39 μM)			(d = 78.80 μM)			(d = 118.17 μM)
	(17)	Num	Error %	(17)	Num	Error %	(17)	Num	Error %	(17)	Num	Error %	(17)	Num	Error %
0	0.9999	1	0.01	0.9955	0.9955	0.00	0.8889	0.8889	0.00	0.5801	0.5773	0.46	0.1895	0.1908	0.69
0.2	0.9999	1	0.01	0.9957	0.9957	0.00	0.8933	0.8933	0.00	0.5965	0.5939	0.43	0.2197	0.2200	0.14
0.4	0.9999	1	0.01	0.9962	0.9962	0.00	0.9066	0.9066	0.00	0.6462	0.6440	0.34	0.3115	0.3101	0.45
0.6	0.9999	1	0.01	0.9971	0.9971	0.00	0.9288	0.9288	0.00	0.7295	0.7279	0.22	0.4686	0.4664	0.47
0.8	0.9999	1	0.01	0.9984	0.9984	0.00	0.9599	0.9599	0.00	0.9484	0.8471	0.85	0.6962	0.6947	0.21
1	1	1	0.0	1	1	0.00	1	1	0.00	1	1	0.00	1	1	0.00

	Average deviation		0.01	Average deviation		0.00	Average deviation		0.00	Average deviation		0.38	Average deviation		0.33

4. Results and Discussion

Equations (17), (13), and (14) represent the new closed and simple approximate analytical expressions of the normalized concentrations of oxidized mediator F_O, substrate F_S, and reduced mediator F_R, respectively, for all values of parameters , B_O, and B_S. The current response is given in (18). All possible numerical values of the dimensionless parameters used by Gooding and Hall [9] and in this work are given in Table 2.

Table 2. Possible numerical values for dimensionless parameters used by Gooding and Hall [9] and in this work.

Parameters	Numerical values
Parameters	Gooding and Hall [9]	This work
	10–400	0.01–400
B_O = [Med_OX] _b/β_O	0.00195	0-1
B_S = [S] _b/β_S	0.018, 0.035, 0.07, 0.14	0-1
μ_S = D_M[Med_OX] _b/D_S[S] _b	0.94736	0.05, 0.5

Table 3. Comparison of normalized current I (18) with the numerical results when B_O = 0.1, B_S = 0.01, and μ_S = 0.05 and for various values of

	Normalized current I		Error %
	Analytical	Numerical	Error %
1	0.009	0.009	0
25	0.223	0.223	0
50	0.441	0.441	0
75	0.655	0.652	0.5
100	0.864	0.838	3

4.1. Concentration Profiles

The concentration profiles for all the three species are shown in Figure 2. The condition that the oxidized mediator F_O (17) is consumed by the enzyme reaction, as the mediator moves inwards from the electrode interface, is established in Figure 2. We understand that when the substrate concentration F_S (13) is changed slightly across the matrix, the oxidized mediator is limiting the reaction under these conditions rather than the substrate itself. The reduced mediator concentration F_R (14) has the reciprocal variation as expected from (9d). The maximum reduced mediator concentration is noticed at the same position in the enzyme layer, as the oxidized species becomes completely consumed.

4.2. Variations in the Thiele Modulus

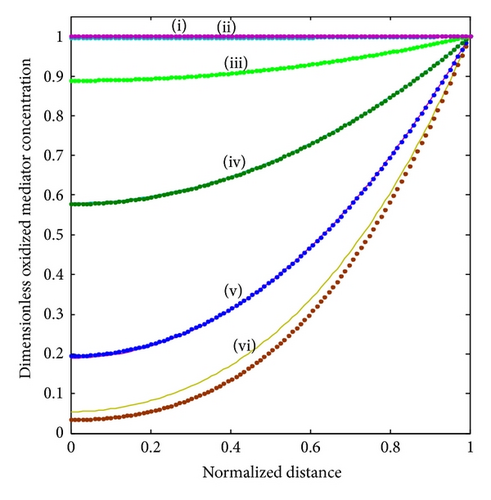
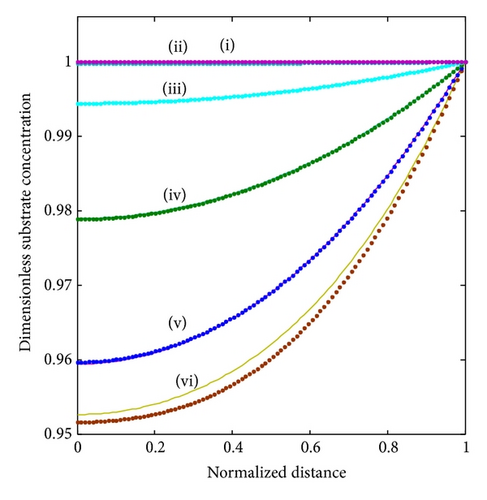
The Thiele modulus essentially compares the reaction and diffusion in the enzyme layer. We examine the rise and downfall of concentration profiles in two cases. (a) When is less than 1, the kinetics dominate and the uptake of oxygen and substrate is kinetically controlled. The overall kinetics are governed by the total amount of active enzyme. (b) The response is under diffusion control, when the Thiele modulus is large , which is observed at high catalytic activity and great membrane thickness or low diffusion coefficient values.

In Figure 3, under the consideration of lower and the sensor under kinetic control, the concentration profile varies slightly from nonenzyme linked oxygen. As increases, the oxidized mediator concentration is consumed in the enzyme reaction. Therefore, the profile deviates more from the linearity. Furthermore, all the oxygen within the polymer matrix is consumed well before reaching the electrode. Thus, the concentration gradient nears the electrode, and hence the flux of oxygen at the electrode surface decreases. We observe that, for a given layer and hence value of , the concentration profiles are also altered according to the bulk concentrations of the substrate and cosubstrate. Thus, with increasing [S] _b the concentration profile deviates from the response where no oxygen is consumed. Thus, an increased substrate concentration F_S causes a decrease in the flux to the electrode. The concentration of the reduced mediator F_R increases in direct proportion to the thickness of the enzyme layer or the amount of enzyme immobilized in the matrix.

In Figure 4, the concentrations of the oxidized mediator, substrate, and reduced mediator are shown for different substrate concentrations in the bulk electrolyte. In the absence of substrate (B_S ≤ 0.001), a straight line is observed for the mediator profile. With increasing substrate concentration in the bulk electrolyte, the profile of reduced mediator bends upward as the generation of reduced mediator by the enzyme reaction increases. The profiles for oxidized mediator and substrate bend downwards.

4.3. Current Response

The parameter of the greatest interest in an amperometric biosensor is the current. For a particular membrane, the variation in can be achieved practically, by varying the thickness of the membrane d or the loading of the enzyme [E_T]. As can be seen in (8), the thickness appears as a squared term and thus small changes will have a much more pronounced effect on the response of the enzyme electrode than the enzyme loading. The variation in current for various values of d and hence is shown in Figure 5. It is evident from the figure that the current I (18) increases when increases. Furthermore, when B_O and B_S are greater than 0.5, all the curves reach the steady-state value. Electroanalytical systems for high spatial resolution scanning and fabrication of micronano sensors need the three-dimensional study of current response.

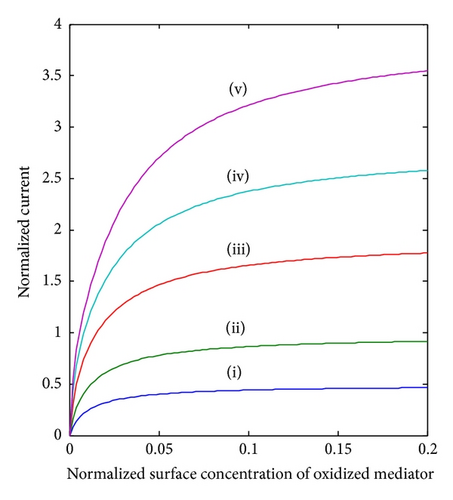
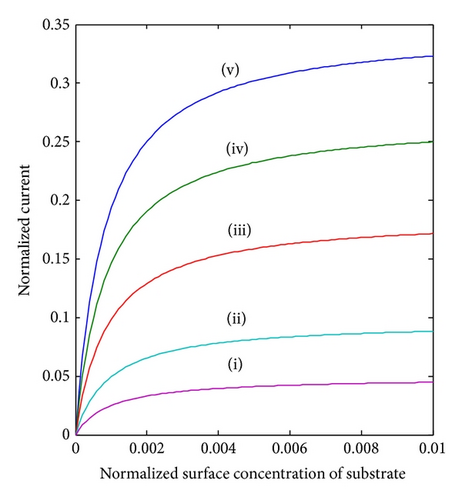
5. Conclusions

This paper presents a theoretical treatment of an oxidized enzyme-membrane electrode in an amperometric biosensor. In this paper, we have solved the nonlinear differential equations both analytically and numerically. The approximate analytical expressions for the steady-state concentrations of oxidised mediator, substrate, and reduced mediator for all values of parameters , B_O, and B_S at the enzyme-membrane electrode geometry are obtained using the Adomian decomposition method. A satisfactory agreement with the numerical result is noted. The analytical results obtained in this paper can be used to analyze the effect of different parameters such as membrane thickness, type of buffer in the external solution and enzyme loading in the membrane. This theoretical result is also useful for the optimization of the biosensor.

Symbols

[E_T]:: Total enzyme concentration (mM)
[E_OX]:: Enzyme concentration of the oxygen (mM)
[ES]:: Enzyme concentration of the substrate (mM)
[E_red]:: Reduced enzyme concentration (mM)
[Med_OX]:: Concentration of oxidized mediator at any position in the enzyme layer (mM)
[Med_red]:: Concentration of reduced mediator at any position in the enzyme layer (mole cm⁻³)
D_M:: Diffusion coefficient of oxidized mediator (cm²s⁻¹)
D_S:: Diffusion coefficient of substrate (cm²s⁻¹)
d:: Thickness of the planar matrix (cm)
[Med_OX] _b:: Oxidized mediator concentration at the enzyme layer ∣electrode boundary (mM)
[Med_OX] _∞:: Oxidized mediator concentration in bulk solution (mM)
[S]:: Concentration of substrate at any position in the enzyme layer (mM)
[S] _b:: Substrate concentration at the enzyme layer|electrode boundary (mM)
[S] _∞:: Substrate concentration in bulk solution (mM)
k₁, k₃, k₄:: Rate constants (M⁻¹s⁻¹)
k₋₁, k₂:: Rate constants (s⁻¹).

Greek Symbols

:: Thiele modulus for the oxidized mediator (none).

Subscripts

OX:: Oxidized
T:: Total
red:: Reduced
O:: Oxygen
S:: Substrate
P:: Product
R:: Reduced
b:: Boundary
∞:: Bulk.

Acknowledgments

This work was supported by the Council of Scientific and Industrial Research (CSIR no.: 01(2442)/10/EMR-II), Government of India. The authors also thank Mr. M. S. Meenakshisundaram, Secretary, The Madura College Board, Dr. R. Murali, the Principal, and Professor S. Thigarajan, HOD, Department of Mathematics, The Madura College, Madurai, Tamil Nadu, India, for their constant encouragement. The author S. Loghambal is very thankful to the Manonmaniam Sundaranar University and V V college of Engineering, Tirunelveli, for allowing the research work.

Appendices

A. Basic Concept of the Adomian Decomposition Method (ADM)

Adomian decomposition method [26–31] depends on decomposing the nonlinear differential equation

()

into the two components

()

where L and N are the linear and the nonlinear parts of F, respectively. The operator L is assumed to be an invertible operator. Solving for L(y(χ)) leads to

()

Applying the inverse operator L on both sides of (A.3) yields

()

where φ(χ) is a function that satisfies the condition L(φ(χ)) = 0. Now assuming that the solution y can be represented as infinite series of the form,

()

where

()

Then equating the terms in the linear system of (A.5) gives the recurrent relation

()

However, in practice all the terms of series in (A.5) cannot be determined, and the solution is approximated by the truncated series

B. Analytical Expression of Concentrations of Oxidized Mediator Using the Adomian Decomposition Method

To solve (15) using the Adomian decomposition method [21–23], we write (15) in the operator form

()

where

()

Applying the inverse operator L⁻¹ on both sides of (B.1) yields

()

According to the ADM, the solution F_O(χ) can be elegantly computed by using the recurrence relation

()

where A_n are the Adomian polynomials of F_O,1, F_O,2, …, F_O,n. We can find the first few Adomian polynomial coefficients A_n using (A.6) as follows:

()

The remaining polynomials A_i(χ) can be generated easily, using (A.6). Apply the following boundary conditions:

()

From (B.4) and using the above conditions we obtain the following results:

()

Adding (B.7)–(B.9), we get the concentration of oxidized mediator (17) in the text. From this solution of the oxidized mediator, the concentration profiles for the substrate and reduced mediator can be obtained using (13) and (14).

C. Scilab/Matlab Program

Scilab/Matlab program for the numerical solution of the systems of nonlinear equations (9a)–(9c) is given below.

function pdex4
m = 0;
x = ;
t = ;
sol = pdepe(m,@pdex4pde,@pdex4ic,@pdex4bc,x,t);
u1 = sol(:,:,1);
u2 = sol(:,:,2);
u3 = sol(:,:,3);
figure
plot(x,u1(end,:))
xlabel(‘Distance x’)
ylabel(‘u1(x,2)’)
figure
plot(x,u2(end,:))
xlabel(‘Distance x’)
ylabel(‘u2(x,2)’)
figure
plot(x,u3(end,:))
xlabel(‘Distance x’)
ylabel(‘u3(x,2)’)
% –––––––––––––––––––––––––––––––
function [c, f, s] = pdex4pde(x,t,u,DuDx)
Bs = 0.01;
Bo = 0.1;
A = 10;
us = 0.05;
up = 1;
c = [1; 1; 1];
f = [1; 1; 1].* DuDx;
F1 =-A ^∧2*(u(1)*u(2)/(u(1)/Bs+u(2)/Bo+(u(1)*u(2))));
F2 =-us*A ^∧2*(u(1)*u(2)/(u(1)/Bs+u(2)/Bo+(u(1)*u(2))));
F3 =up*A ^∧2*(u(1)*u(2)/(u(1)/Bs+u(2)/Bo+(u(1)*u(2))));
s = [F1; F2; F3];
% –––––––––––––––––––––––––––––––
function u0 = pdex4ic(x);
u0 = [1; 0; 1];
% –––––––––––––––––––––––––––––––
function [pl,ql,pr,qr] = pdex4bc(xl,ul,xr,ur,t)
pl = [0; 0; 0];
ql = [1; 1; 1];
pr = [ur(1)-1; ur(2)-1; ur(3)];
qr = [0; 0; 0];

D. Nomenclature

References

1 Simon E., Halliwell C. M., Toh C. S., Cass A. E. G., and Bartlett P. N., Immobilisation of enzymes on poly(aniline)-poly(anion) composite films. Preparation of bioanodes for biofuel cell applications, Bioelectrochemistry. (2002) 55, no. 1-2, 13–15, 2-s2.0-0036148091, https://doi.org/10.1016/S1567-5394(01)00160-8.
Google Scholar
2 Liu Y., Zhang X., Liu H., Yu T., and Deng I., Immobilization of glucose oxidase onto the blend membrane of poly(vinyl alcohol) and regenerated silk fibroin: morphology and application to glucose biosensor, Journal of Biotechnology. (1996) 46, no. 2, 131–138, https://doi.org/10.1016/0168-1656(95)00182-4.
Google Scholar
3 Trevan M. D., Immobilised Enzymes, 1981, 2nd edition, Wiley, New York, NY, USA.
Google Scholar
4 Nguyen Q. T., Ping Z., Nguyen T., and Rigal P., Simple method for immobilization of bio-macromolecules onto membranes of different types, Journal of Membrane Science. (2003) 213, no. 1-2, 85–95, 2-s2.0-0037359867, https://doi.org/10.1016/S0376-7388(02)00515-X.
Google Scholar
5 Bhardwaj A., Jinbo L., Glauner K., Ganapathi S., Bhattacharyya D., and Allan Butterfield D., Biofunctional membranes: an EPR study of active site structure and stability of papain non-covalently immobilized on the surface of modified poly(ether)sulfone membranes through the avidin-biotin linkage, Journal of Membrane Science. (1996) 119, no. 2, 241–252, 2-s2.0-0030269426, https://doi.org/10.1016/0376-7388(96)00124-X.
Google Scholar
6 Guilbault G. G., K. Mosbach, Immobilised enzymes and cells, Methods in Enzymology, 1988, Academic press, New York, NY, USA.
Google Scholar
7 Robeson L. M., Correlation of separation factor versus permeability for polymeric membranes, Journal of Membrane Science. (1991) 62, no. 2, 165–185, https://doi.org/10.1016/0376-7388(91)80060-J.
Google Scholar
8 Gronda A. M., Buechel S., and Cussler E. L., Mass transfer in corrugated membranes, Journal of Membrane Science. (2000) 165, no. 2, 177–187, 2-s2.0-0033982874, https://doi.org/10.1016/S0376-7388(99)00230-6.
Google Scholar
9 Gooding J. J. and Hall E. A. H., Practical and theoretical evaluation of an alternative geometry enzyme electrode, Journal of Electroanalytical Chemistry. (1996) 417, no. 1-2, 25–33, https://doi.org/10.1016/S0022-0728(96)04752-3.
Google Scholar
10 Leypoldt J. K. and Gough D. A., Model of a two-substrate enzyme electrode for glucose, Analytical Chemistry. (1984) 56, no. 14, 2896–2904, 2-s2.0-0021646139.
Google Scholar
11 Gooding J. J. and Hall E. A. H., Parameters in the design of oxygen detecting oxidase enzyme electrodes, Electroanalysis. (1996) 8, no. 5, 407–413, 2-s2.0-0001358471.
Google Scholar
12 Ying L., Kang E. T., and Neoh K. G., Covalent immobilization of glucose oxidase on microporous membranes prepared from poly(vinylidene fluoride) with grafted poly(acrylic acid) side chains, Journal of Membrane Science. (2002) 208, no. 1-2, 361–374, https://doi.org/10.1016/S0376-7388(02)00325-3.
Google Scholar
13 Turmanova S., Trifonov A., Kalaijiev O., and Kostov G., Radiation grafting of acrylic acid onto polytetrafluoroethylene films for glucose oxidase immobilization and its application in membrane biosensor, Journal of Membrane Science. (1997) 127, no. 1, 1–7, 2-s2.0-0030616148, https://doi.org/10.1016/S0376-7388(96)00277-3.
Google Scholar
14 Pallaeschi G. and Turner A. P. F., Amperometric tetrathiafulvalene-mediated lactate electrode using lactate oxidase absorbed on carbon foil, Analytica Chimica Acta. (1990) 234, 459–463, https://doi.org/10.1016/S0003-2670(00)83591-6.
Google Scholar
15 Ohara T. Y., Rajagopalan R., and Hellcr A., Research Article Glucose electrodes based on cross-linked bis(2,2′-bipyridine)chloroosmium(+/2+) complexed poly(1-vinylimidazole) films, Analytical Chemistry. (1993) 65, no. 23, 3512–3517, https://doi.org/10.1021/ac00071a031.
Google Scholar
16 Loghambal S. and Rajendran L., Mathematical modeling in amperometric oxidase enzyme-membrane electrodes, Journal of Membrane Science. (2011) 373, no. 1-2, 20–28, 2-s2.0-79953750253, https://doi.org/10.1016/j.memsci.2011.02.033.
Google Scholar
17 Martens N. and Hall E. A. H., Model for an immobilized oxidase enzyme electrode in the presence of two oxidants, Analytical Chemistry. (1994) 66, no. 17, 2763–2770, https://doi.org/10.1021/ac00089a026.
Google Scholar
18 Gooding J. J., Hämmerle M., and Hall E. A. H., An enzyme electrode with response independent of the thickness of the enzyme layer, Sensors and Actuators B. (1996) 34, no. 1-3, 516–523, 2-s2.0-0042545838.
Google Scholar
19 Adomian G., Convergent series solution of nonlinear equations, Journal of Computational and Applied Mathematics. (1984) 11, no. 2, 225–230, https://doi.org/10.1016/0377-0427(84)90022-0.
Google Scholar
20 Loghambal S. and Rajendran L., Mathematical modeling of a tubular spectrochemical cell using the finite Hankel transformation, Russian Journal of Electrochemistry. (2011) 47, no. 8, 883–889, 2-s2.0-80052684604, https://doi.org/10.1134/S1023193511080088.
Google Scholar
21 Anitha S., Subbiah A., and Rajendran L., Approximate analytical solution of non-linear reaction’s diffusion equation at conducting polymer ultra microelectrodes, ISRN Physical Chemistry. (2012) 12, 1–12.
Google Scholar
22 Adomian G., Journal of computational and applied mathematics, Convergent Series Solution of Nonlinear Equations. (1984) 11, 225–230, https://doi.org/10.1016/0377-0427(84)90022-0.
Google Scholar
23 Patel A. and Serrano S. E., Decomposition solution of multidimensional groundwater equations, Journal of Hydrology. (2011) 397, no. 3-4, 202–209, 2-s2.0-78651362981, https://doi.org/10.1016/j.jhydrol.2010.11.032.
Google Scholar
24 Mohamed M. A., Comparison differential transformation technique with adomian decomposition method for dispersive long-wave equations in (2+1)-dimensions, Applications and Applied Mathematics. (2010) 5, no. 1, 148–166.
Google Scholar
25 Jaradat O. K., Adomian decomposition method for solving abelian differential equations, Journal of Applied Sciences. (2008) 8, no. 10, 1962–1966, https://doi.org/10.3923/jas.2008.1962.1966.
Google Scholar
26 Siddiqui A. M., Hameed M., Siddiqui B. M., and Ghori Q. K., Use of Adomian decomposition method in the study of parallel plate flow of a third grade fluid, Communications in Nonlinear Science and Numerical Simulation. (2010) 15, no. 9, 2388–2399, 2-s2.0-77949489909, https://doi.org/10.1016/j.cnsns.2009.05.073.
Google Scholar
27 Wazwaz A.-M. and Gorguis A., An analytic study of Fisher′s equation by using Adomian decomposition method, Applied Mathematics and Computation. (2004) 154, no. 3, 609–620, 2-s2.0-3042836089, https://doi.org/10.1016/S0096-3003(03)00738-0.
10.1016/S0096-3003(03)00738-0
Google Scholar
28 Biazar J. and Islam R., Solution of wave equation by Adomian decomposition method and the restrictions of the method, Applied Mathematics and Computation. (2004) 149, no. 2, 807–814, https://doi.org/10.1016/S0096-3003(03)00186-3.
10.1016/S0096-3003(03)00186-3
Google Scholar
29 Sweilam N. H. and Khader M. M., Approximate solutions to the nonlinear vibrations of multiwalled carbon nanotubes using Adomian decomposition method, Applied Mathematics and Computation. (2010) 217, 495–505, https://doi.org/10.1016/j.amc.2010.05.082.
Web of Science® Google Scholar
30 Adomian G., Solving the mathematical models of neurosciences and medicine, Mathematics and Computers in Simulation. (1995) 40, no. 1-2, 107–114, https://doi.org/10.1016/0378-4754(95)00021-8.
Google Scholar
31 Adomian G. and Witten M., Computation of solutions to the generalized Michaelis-Menton equation, Applied Mathematics Letters. (1994) 7, 45–48, https://doi.org/10.1016/0893-9659(94)90009-4.
Google Scholar

Citing Literature

All articles

Analytical Expressions for Steady-State Concentrations of Substrate and Oxidized and Reduced Mediator in an Amperometric Biosensor

Abstract

1. Introduction