Describing the Dynamics and Complexity of Matsumoto-Nonaka′s Duopoly Model
Abstract
We study the duopoly model proposed by Matsumoto and Nonaka (2006), in which two firms produce two complementary goods, and there are externalities of different signs. We analyze the topological complexity of the model by computing its topological entropy with prescribed accuracy, and, in addition, we show when such topological complexity is physically observable by characterizing the attractors. Finally, we exploit the fact that reaction maps have negative Schwarzian derivative to show the existence of absolutely continuous (with respect to Lebesgue measure) ergodic measures, and, as an economic application, we compute the average profit for almost all initial conditions.
1. Introduction: The Model and Our Aims
In [1] a two-market model consisting in two firms, which produce differentiated goods is introduced. The first firm produces good x in the first market, and the second one produces good y in the second market. It is assumed that externalities of different signs exist. An externality occurs when the actions of firms directly affect the production capabilities of other firms other than through the price mechanism of the market. In this case, the positive externality comes from the market demand; that is, the sales possibilities of one firm are positively influenced by the production of the other firm. The negative externality is due to the cost functions of each firm, since the cost depends not only on its own production but also on the other firm’s production.
Our aims are, on one hand, to give an analytical proof of the existence of chaos in the model. This proof will be given by computations of topological entropy of the system with prescribed accuracy. As positive topological entropy will imply the existence of chaos in the sense of Li and Yorke, we will be able to give a proof of existence of chaos for a wide range of parameter values. On the other hand, we will be able to describe the nature of attractors of the system, and we will go beyond to the seminal work [1] proving the existence of absolutely continuous ergodic measures. The existence of such measures will allow us to obtain some consequences from both dynamic and economic points of view. Finally, we must emphasize that our approach is somewhat different from that made in [2]. Moreover, our scheme can be adapted to analyze the dynamics of models given by maps with the form of Rα,β.
The paper is organized as follows. In Section 2 we study the complexity of the model. For that, we compute the topological entropy using different algorithms depending on the number of pieces of monotonicity of the functions involved in the model. As an approach to the attractors, their number is studied in Section 3. On one hand, the fact that the Schwarzian derivative of the function is negative allows us to know the possibilities of the metric attractors that can appear. On the other hand, a real computation of the attractors allows us to realize that topological chaos need not be physically observed, with the Lyapunov exponents being the key for analyzing these phenomena. The Lyapunov exponent gives us the key to study that situation. Invariant measures and average profits are considered in Section 4. Finally, Section 5 is devoted to conclusions.
2. Computing Topological Entropy
The goal of this section is to compute the topological entropy of the system. Topological entropy was introduced in [3] by Adler, Konheim, and McAndrew. When f is a continuous piecewise monotone function, the Misiurewicz-Szlenk′s theorem, [4], gives us the following characterization of the topological entropy h(f).
Theorem 1. Let f: [0,1] → [0,1] be a piecewise continuous monotone functions and c(f) the number of pieces of monotonicity. Then,
Next, we must recognize that Misiurewicz-Szlenk formula is not useful for computing topological entropy of our model, so we are forced to use numerical algorithms which are based on the number of monotone pieces of Fα,β and Gα,β. Therefore, we will make a precise description of monotonicity regions for these maps.
2.1. Monotonicity Regions of Fα,β and Gα,β
We study the shape of the composition map, where shape means in this case the number of pieces of monotonicity that each map has depending on the values of the parameters α and β. This will be used in the next section to compute the topological entropy.
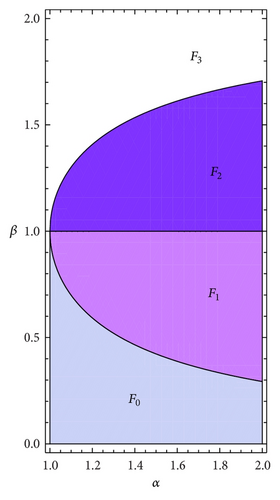
- (i)
Fα,β is a monotone decreasing map if (α, β) ∈ F0, where
() -
see example for α = 1.5 and β = 0.3 in Figure 2(a).
- (ii)
Fα,β is a unimodal map with a minimum for if (α, β) ∈ F1, where
() -
see example for α = 1.5 and β = 0.8 in Figure 2(b).
- (iii)
Fα,β is a bimodal map with a minimum for and a maximum for x = 1/β if (α, β) ∈ F2, where
() -
see example for α = 1.5 and β = 1.2 in Figure 2(c).
- (iv)
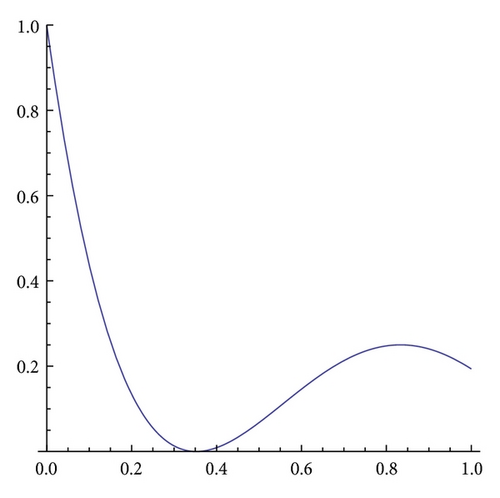
Fα,β is a trimodal map with two minima (for and ) and a maximum for x = 1/β if (α, β) ∈ F3, where
() -
see example for α = 1.5 and β = 1.8 in Figure 2(d).
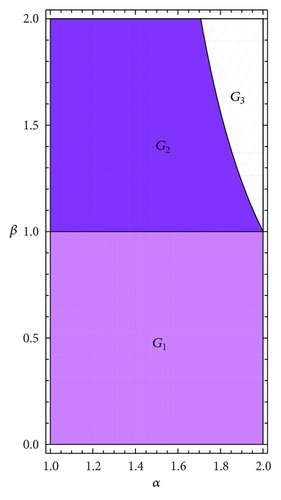

- (i)
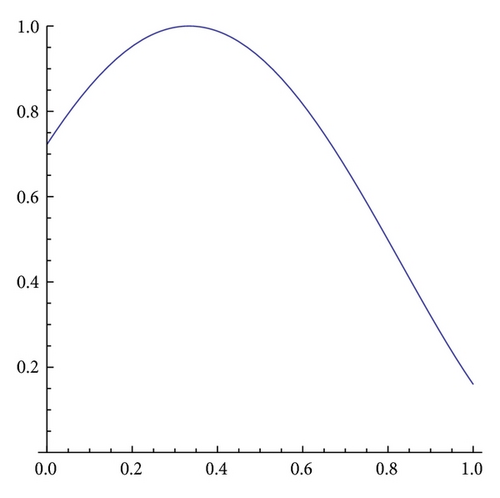
Gα,β is a unimodal map with a maximum (for x = 1 − 1/α) if (α, β) ∈ G1, where
() -
see example for α = 1.5 and β = 0.6 in Figure 3(a).
- (ii)
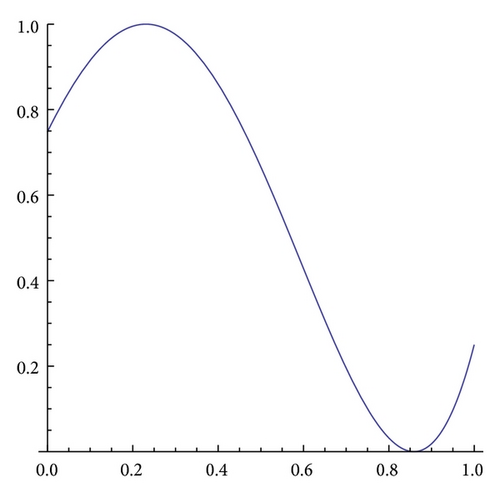
Gα,β is a bimodal map with a maximum for x = 1 − 1/α and a minimum for if (α, β) ∈ G2, where
() -
see example for α = 1.3 and β = 1.5 in Figure 3(b).
- (iii)
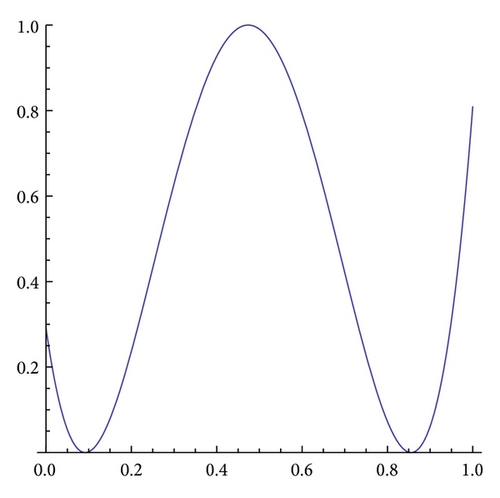
Gα,β is a trimodal map with a maximum for x = 1 − 1/α and two minima in the points and if (α, β) ∈ G3, where
() -
see example for α = 1.9 and β = 1.9 in Figure 3(c).
2.2. Practical Computation of Topological Entropy
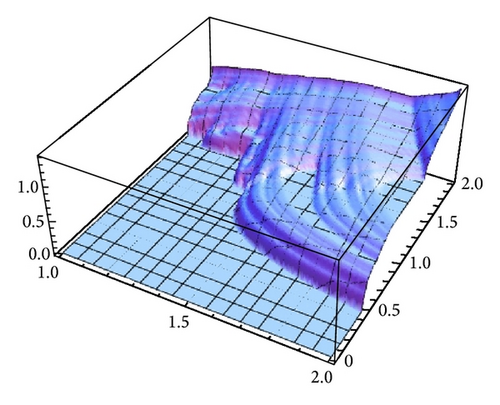
Algorithms for computing the topological entropy for the special case of unimodal maps are given in [6, 7]. An algorithm for bimodal maps (with three pieces of monotonicity) is described in [8], and an algorithm for a particular class of piecewise continuous maps with four pieces of monotonicity is described in [9]. These three types of algorithms cover all the cases involved in the dynamical system that we are considering for the composition maps Fα,β and Gα,β. The results obtained for the model can be observed in Figure 4.
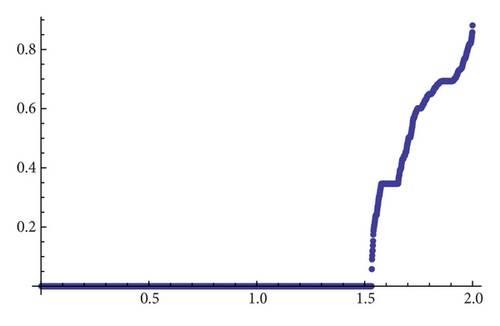
Figures 5(a), 5(b), 5(c), and 5(d) show the topological entropy with accuracy 10−4, where α takes the values 1.25, 1.30, 1.50, and 1.85.
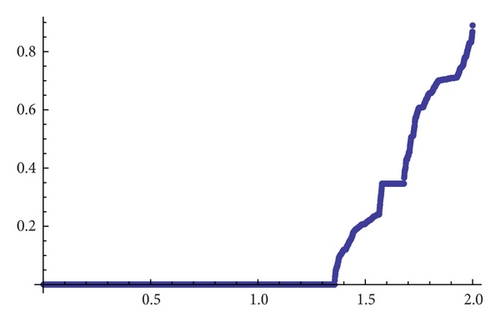
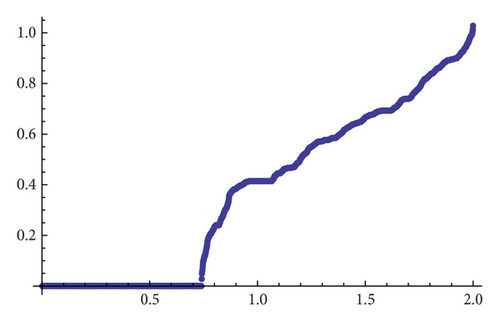

For β = 1.1, and β = 1.15 the topological entropy with accuracy 10−4 is given by Figures 6(a) and 6(b).
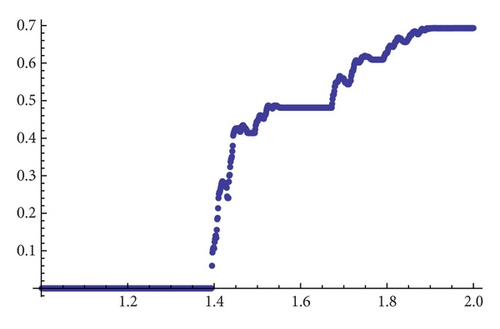
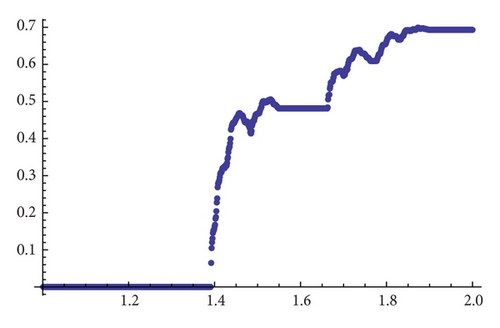
2.3. Existence of Chaotic Maps
Positive topological entropy implies chaos in the sense of Blanchard et al. [10], and therefore, the above computations of topological entropy are an analytical proof of the existence of chaos in the model. Even more, we can prove that positive topological entropy is equivalent to chaos in the sense of Li-Yorke. For that, we just need to notice that when the topological entropy is equal to zero, the map is not chaotic because the relative extreme points of the composition maps fα∘gβ and gβ∘fα are nonflat since the second derivative in these points is nonzero, (remember that a critical point is nonflat if some higher derivative is nonzero). Then, by [11, Theorem A], C∞ maps with nonflat turning points have no wandering intervals (i.e., for a continuous interval map f, an interval J is called wandering if J, f(J), f(J) 2, … are disjoint and no point x ∈ J is asymptotically periodic), and by [12, Lemma 2.7], a map with zero topological entropy is chaotic if and only if it has wandering intervals. Hence, our model is not chaotic when the topological entropy is zero.
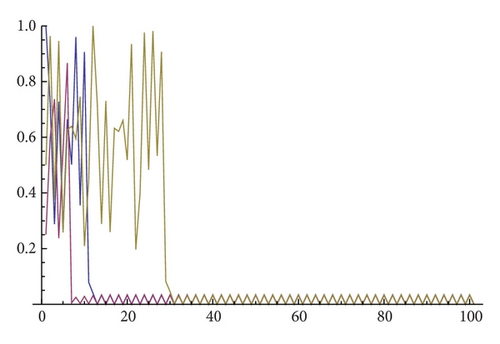
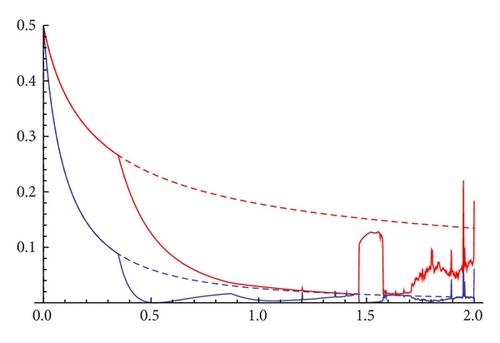
Therefore, we have two regions the nonchaotic one where every trajectory has the property that for any ϵ > 0 there is a periodic trajectory which is ϵ close to it [13]. In practice, one might check that a computer simulation shows the convergence to a periodic orbit when parameters are in the nonchaotic region. For the second region one could expect a similar situation, but as we will show in the next section, the topological chaos we have shown to exist, could not be observed. For instance, for α = 1.8 and β = 1.85, the topological entropy of gβ∘fα is positive, but the time series of several orbits reveal a periodic motion (see Figure 7).
3. Chaos, Attractors, and Schwarzian Derivative
We start this section with some useful definitions. Let f : I → I be a map. A probabilistic measure μ is said to be invariant for f if μ(A) = μ(f−1(A)) for any Borel set A ⊂ I. In addition, the measure is ergodic if the equality f(A) = A implies that μ(A) = 0 or 1. Denote by ℳ(X, f) and ℰ(X, f) the set of invariant and ergodic measures of f, respectively.
Given x ∈ I, define its ω-limit set ω(x, f) as the set of limits points of its orbit. Recall that a metric attractor is a subset A ⊂ [0,1] such that f(A)⊆A, O(A) = {x : ω(x, f) ⊂ A} has positive Lebesgue measure, and there is no proper subset A′A with the same properties. O(A) is called the basin of the attractor.
- (A1)
A periodic orbit (recall that x is periodic if fn(x) = x for some n ∈ ℕ).
- (A2)
A solenoidal attractor, which is basically a Cantor set in which the dynamics is quasiperiodic. More precisely, the dynamics on the attractor is conjugated to a minimal translation, in which each orbit is dense on the attractor. The dynamics of f restricted to the attractor is simple; neither positive topological entropy nor Li-Yorke chaos can be obtained. Its dynamics is often known as quasiperiodic.
- (A3)
A union of periodic intervals, J1, …, Jk, such that fk(Ji) = Ji and fk(Ji) ≠ Jj, 1 ≤ i < j ≤ k, and such that fk is topologically mixing. Topologically mixing property implies the existence of dense orbits on each periodic interval (under the iteration of fk).
Since S(f∘g)(x) = Sf(g(x))·(g′(x)) 2 + Sg(x) and the maps fα and gβ have negative Schwarzian derivative the same occurs to the composition maps Fα,β and Gα,β. Since attractors of type (A1) must also attract the orbit of a turning point when the map has negative Schwarzian derivative, we have that the number of attractors of Fα,β and Gα,β is bounded to at most 3. Even more, when Fα,β and Gα,β have three monotone pieces, then their value in two turning points agree, which implies that in fact, the number of attractors of Fα,β and Gα,β can be at most 2. The following result shows that the attractors of Fα,β and Gα,β are deeply connected.
Proposition 2. Let f, g : I → I be C1 maps such that ω(x, f∘g) is an attractor of f∘g. Then ω(g(x), g∘f) = g(ω(x, f∘g)) is an attractor of g∘f.
Proof. As usual, denote by λ the one-dimensional Lebesgue measure. Let A ⊂ I with λ(A) > 0 such that for any y ∈ A we have ω(y, f∘g) = ω(x, f∘g). Since f is C1, we have that λ(f−1(A)) > 0. Now, let z ∈ f−1(A), and fix y ∈ A such that y = f(z). For any n ∈ ℕ we have

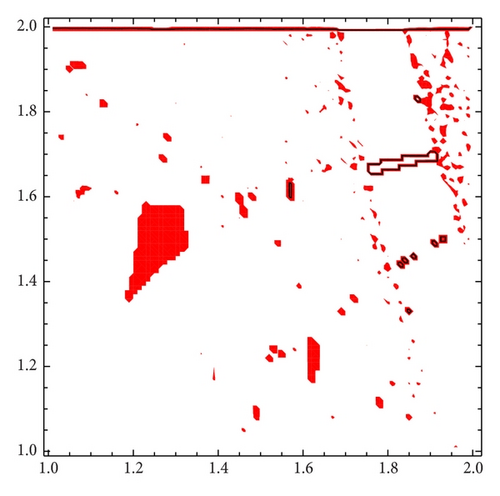
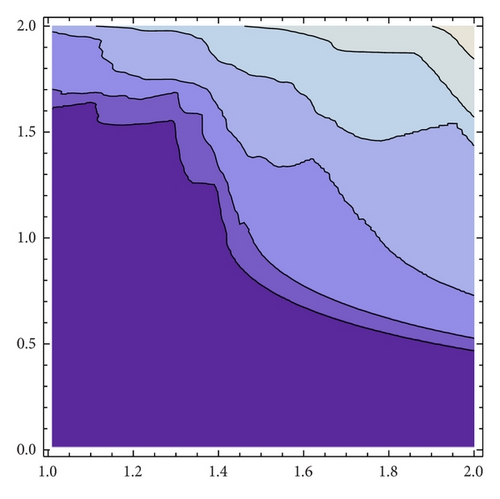
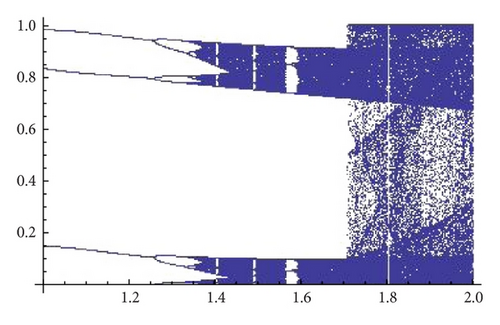
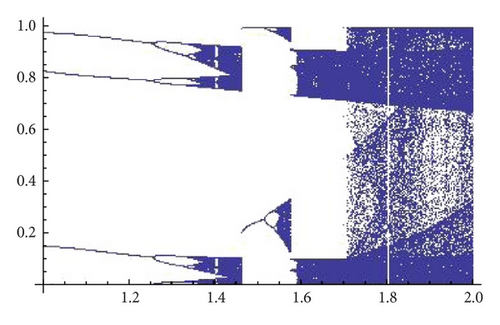
Taking into account the results obtained for generating Figure 8, we see that for α = 1.3 there are values of β around 1.5 for which it seems that two different attractors of Gα,β may coexist. Figure 9 shows a refinement of Figure 8 for α = 1.3 and 1.35. The bifurcation diagrams (see Figure 10) also suggest the existence of two different attractors for α = 1.3 but not for 1.35.
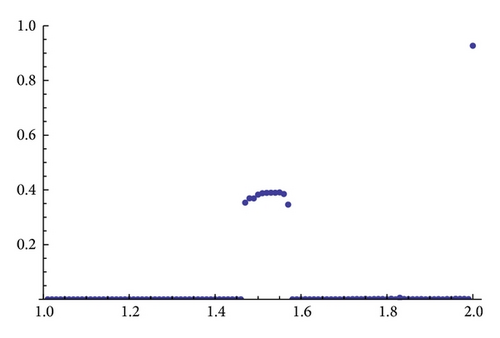
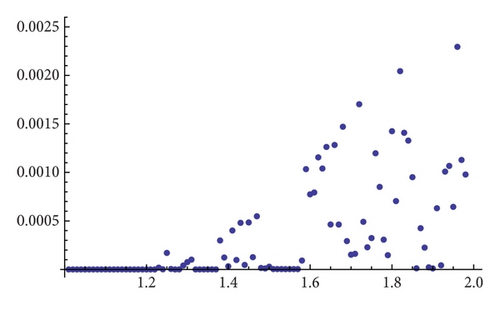
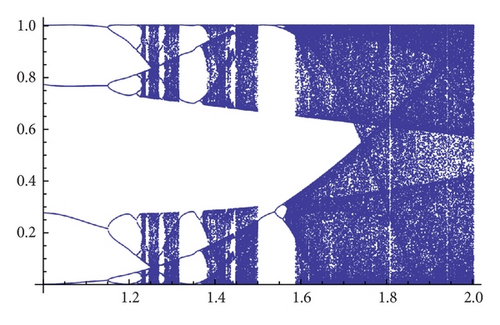
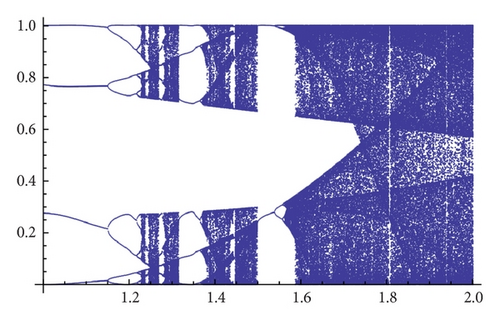
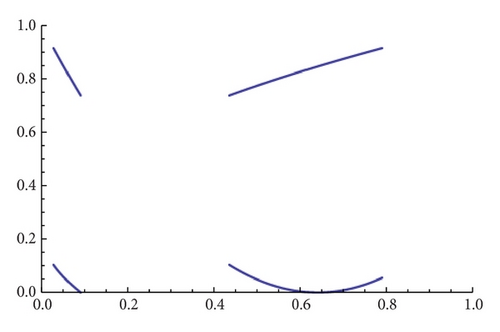
As an example, we show different types of attractors and limit sets (but nonmetric attractors) obtained for the parameter values α = 1.3 and β = 1.56 (see Figure 11 and the explanations therein).
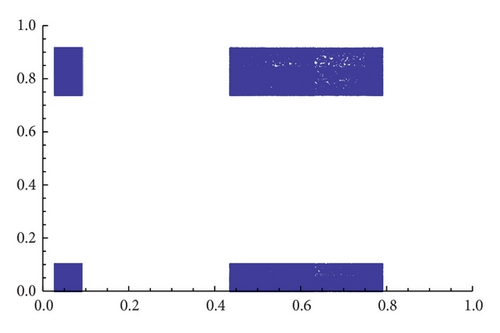
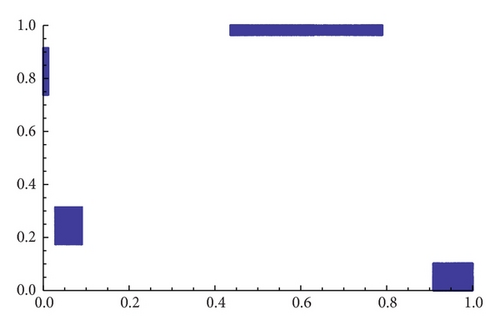
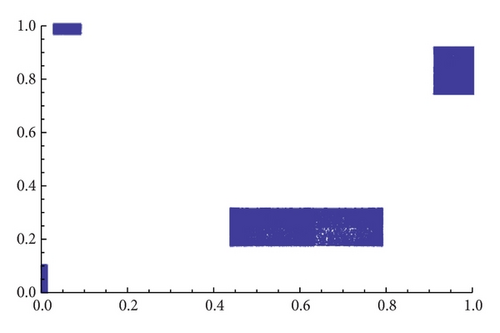
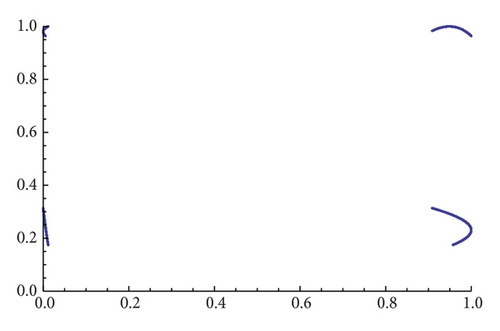
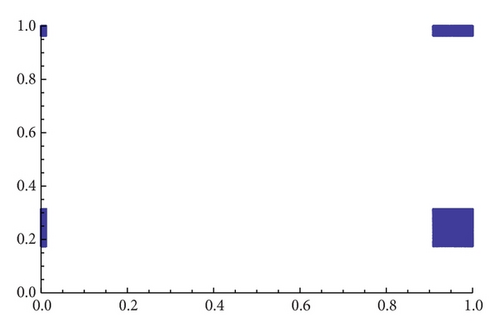
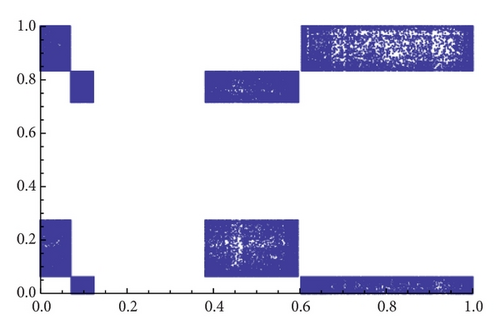
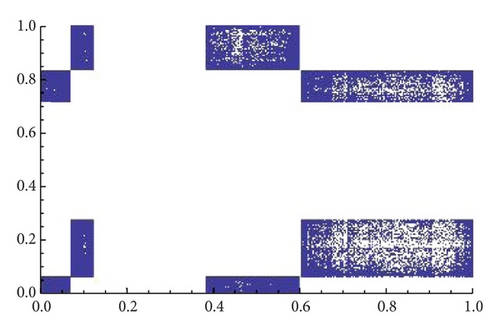
When α = 1.35 the map gβ∘fα seems to have only one attractor, and, for β = 1.2, we see in Figure 12 that several of them may exist (see [18] for an analytical explanation of this fact). Figure 13 shows different types of attractors that can appear when we fix α = 1.86.
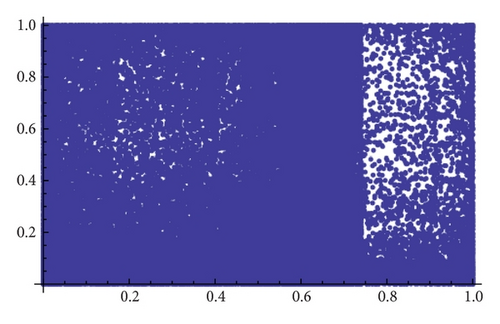
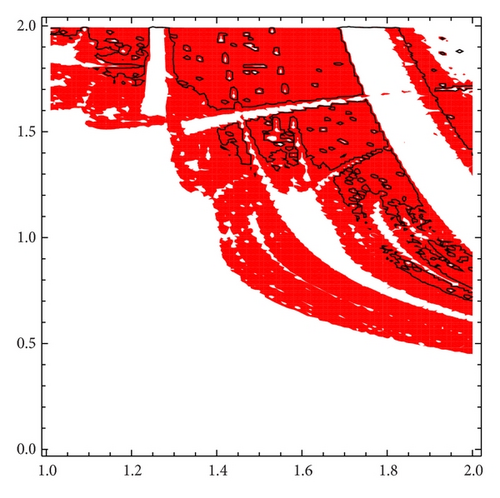
It is observed that there is a white band in the upper right side of the projection; this corresponds with the region where the fixed point is a local attractor. The topological entropy in these points is positive, but the chaos is not physically observable. Figure 14 explains the results obtained in Figure 7 because the parameter values α = 1.8 and β = 1.85 are clearly in a region with negative Lyapunov exponents.
4. On Invariant Measures and Average Profits
- (i)
The map Rα,β may have several attractors. Therefore, we can have several average values.
- (ii)
When we are in the basis of a periodic attractor A = {(x1, y1), …, (xk, yk)}, the equality
() -
trivially holds. Therefore, we must concentrate on attractors constructed from types (A2) and (A3).
- (iii)
Since, computationally, attractors of type (A2) are not easily detected and their probability is small, we must concentrate our efforts on deciding when attractors of type (A3) support an invariant ergodic measure which is absolutely continuous with respect to the Lebesgue measure. Note that, by, for example, [21], the existence of dense orbits is not enough to guarantee the existence of absolutely continuous ergodic measures.
We start with the next result, which states that absolutely continuous ergodic measures of fα∘gβ and gβ∘fα are deeply connected.
Proposition 3. Let f, g : I → I be C1 maps, and let μ ∈ ℰ(I, f∘g) be absolutely continuous with respect to the Lebesgue measure. Then defined by for every Borel set A is an absolutely continuous ergodic measure of g∘f.
Proof. The fact that can be seen in [22]. Now, let h be a density function for μ; that is, μ(A) = ∫A h dλ for any Borel set A. Since
Proposition 3 is a great help in detecting the absolutely continuous ergodic measures of Rα,β; we just consider one map Fα,β or Gα,β and decide whether they have absolutely continuous ergodic measures. The absolutely continuous ergodic measures of Rα,β will be constructed by applying Proposition 3 and taking the product measure, which will be absolutely continuous but probably not ergodic. If we denote the product measure by μ1 × μ2, we take the ergodic decomposition , where , and k is the number of different attractors constructed by the attractors of Fα,β and Gα,β supporting the measures μ1 and μ2. The absolutely continuous ergodic measures are therefore ν1, …, νk. In the case studied in [1] we find that k = 1.
So, we fix a turning point of Fα,β for instance and compute its Lyapunov exponent λ(Fα,β)(c). If it is negative or zero, there is nothing to do. So, we assume that it is positive and let J1, …, Jk be periodic intervals such that is an attractor of type (A3). Any ergodic measure μ supported on must satisfy μ(Ji) = 1/k, i = 1, …, k, and then we can consider , the invariant subinterval Ji for some 1 ≤ i ≤ k, and the ergodic measure (for ) ν given by the formula ν(A) = μ(A∩Ji) · k. Since has negative Schwarzian derivative, by [23], we conclude that ν, and therefore, μ, can be chosen to be absolutely continuous with respect to the one-dimensional Lebesgue measure.
For instance, we consider the values α = 1.3 and β = 1.56. The possible attractors were studied in detail in Figure 11, and we obtained the following average profits for the initial values as we showed in Table 1.
| Initial conditions | Firm 1 | Firm 2 |
|---|---|---|
| x0 = 1/β, y0 = 0 | 0.0179073 | 0.0175666 |
| x0 = 1/β, y0 = 0.001 | 0.0145578 | 0.0161027 |
| x0 = 1/β, y0 = 1 | −0.00460741 | 0.052774 |
| x0 = 1/β, y0 = G(1) | −0.00459554 | 0.0527484 |
| 0.00177609 | 0.125768 | |
| 0.00190711 | 0.12623 |
We compute the average profit for each firm. This result could be different if we change initial conditions when the number of attractors is different from one, as we studied in the previous section. Thus, for each firm we are going to present two different graphics in the square (α, β) ∈ [1,2]2 with two different initial conditions, and we observe the differences between them. In the square (α, β)∈[1,2]×[0,1] there is only at most one turning point. Then we study the number of fixed Cournot points depending on (α, β)∈[1,2]×[0,2]. When there are more than a fixed point we determine in which fixed point the profit is maximum for each firm. Finally we compare the average profit with the profit in the fixed point (in which it is maximum) and compute the residual profit.
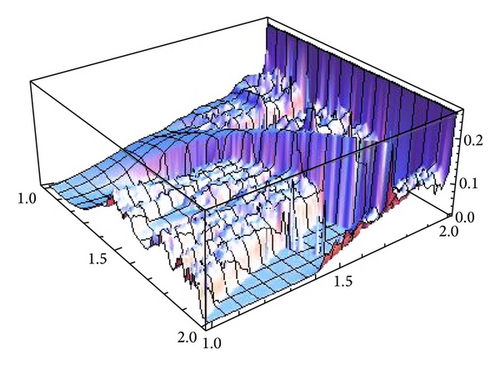
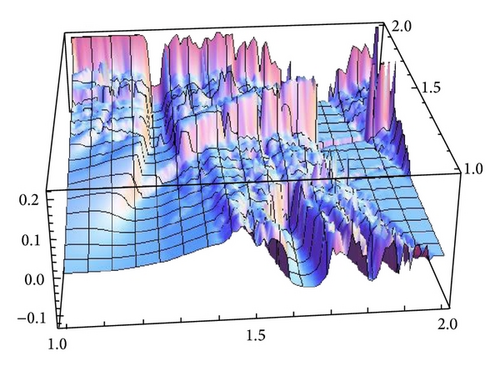
Figure 15 shows the average profit of both firms. For that, we use orbits of length n = 10000 and, as initial conditions, (x, y), where x is the minimum of fα∘gβ when it exists and 0.4, otherwise, and y is the maximum of gβ∘fα. We will denote this election of initial conditions as min-max conditions. When β is greater than one there are more turning points which eventually may produce other average profits as it is shown in Figure 16. Here, we show the profit of firm 1, taking as initial conditions (x, y), where x is the maximum of fα∘gβ and y is the maximum of gβ∘fα, which will be denoted as max-max conditions, and compare the situation with the initial conditions min-max previously computed. Figure 17 shows the same scenario for the second firm.
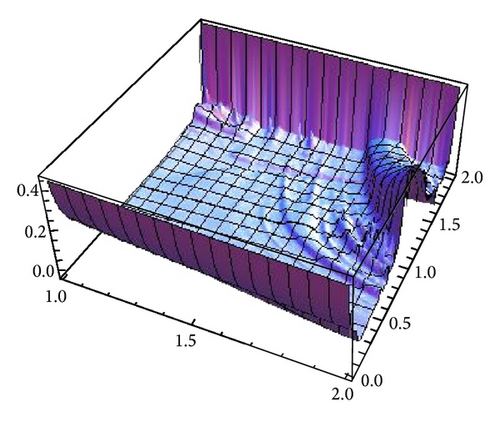
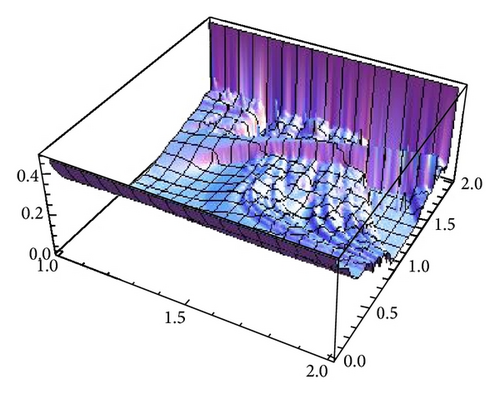
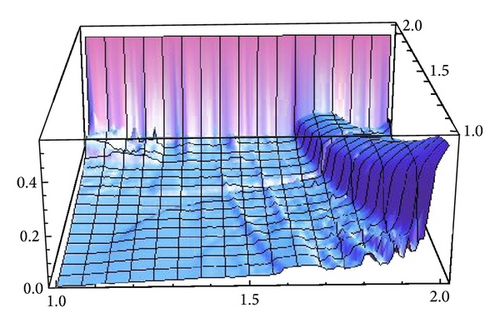
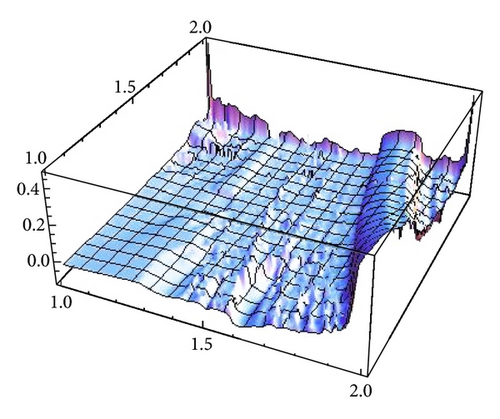
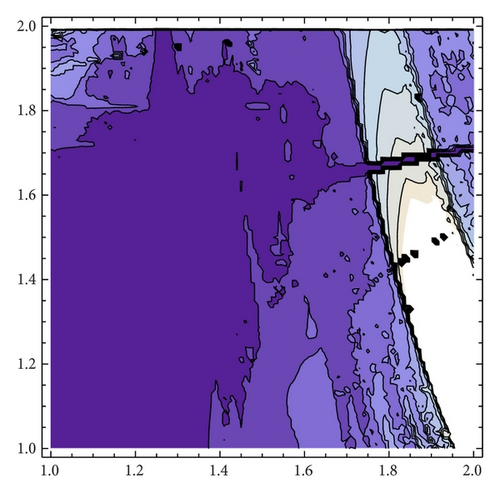
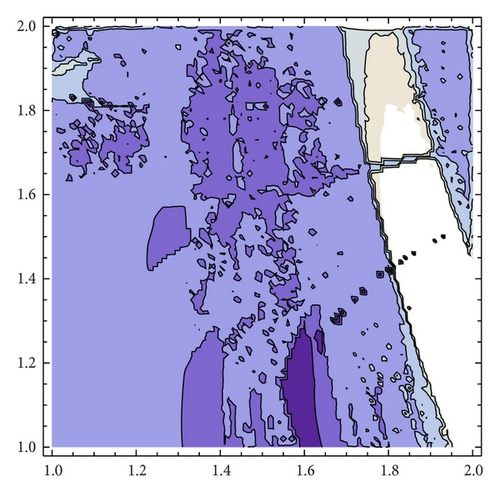
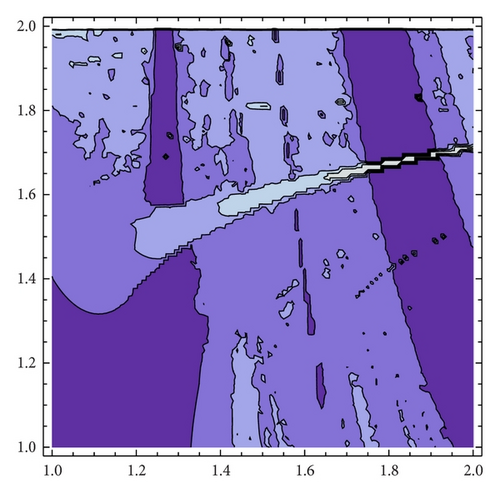
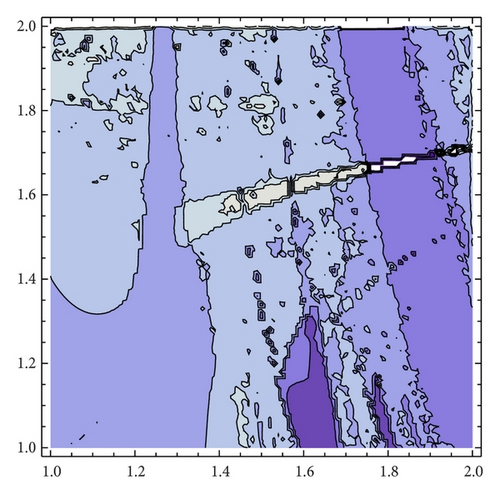
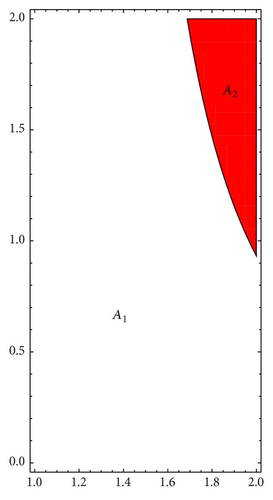
We are interested in analyzing whether the destabilization of Cournot points, even in the chaotic regime, is a good business for both firms. To this end, we compare the average profits of generic orbits with the expected profit at Cournot points. Firstly, we have to compute the number of fixed points of the composition fα∘gβ, which can be seen in Figure 18. The parameter space can be divided into two regions, A1 and A2. In A1 there is one fixed point while in A2 the number of fixed points is three, which will be ordered x1(α, β) ≤ x2(α, β) ≤ x3(α, β). As an exception, for (α, β) = (2,2), the number of fixed points are four. In [1, Theorems 1 and 2] the stability and bifurcation diagrams of stationary points is studied in detail.
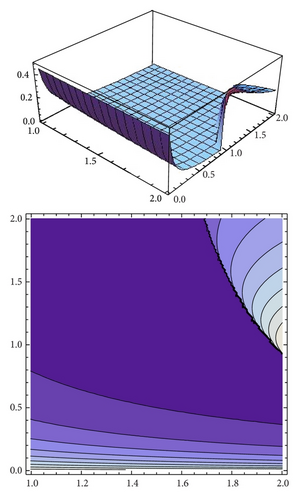
In region A2 we compute the profit of the first firm for each fixed point, and we observe that it is maximum for the fixed point x3(α, β) and minimum for x1(α, β), obtaining the converse situation for the second firm. Figure 19 (resp., Figure 20) shows the profit of the first firm (resp., second firms) against the profit obtained by the second firm (resp., second firm) when the fixed point that maximizes the profit of firm 1 (resp., firm 2) is chosen.
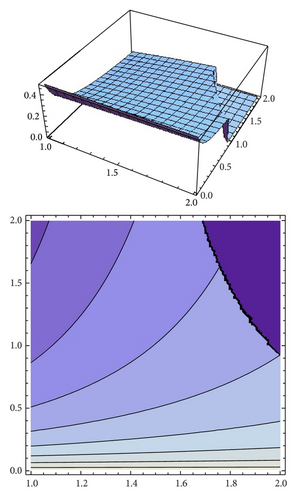
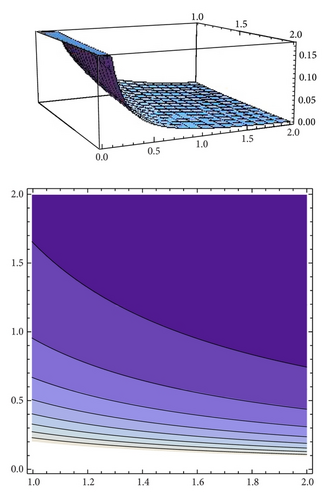
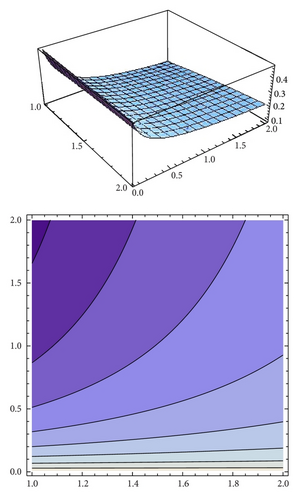
The case α = 1.3 was studied in Figure 11 and Table 1. We compute the profit of both firms in this case to compare the results see Figures 21 and 22.


5. Conclusions
A duopoly model depending on two parameters is studied in detail. By computing its topological entropy we characterize the parameter values which admit the existence of chaotic behavior of trajectories. We also analyze when the above mentioned chaotic trajectories either can be observed or remain on a set of zero Lebesgue measures and therefore are not physically observed in computer simulations. For that, we study the metric attractors of the model concluding that several of them can coexist. The existence of absolutely continuous ergodic measures is proved, and we showed that, even when chaotic maps are considered, the average of economic functions, like profit and production and along the orbits can attain a finite number of values. The existence of such values allows us to make decisions on whether the equilibrium points deserve to be stabilized by choosing strategies that are distinct from naive expectations.
Acknowledgments
This paper has been partially supported by Grants MTM2011-23221 from Ministerio de Ciencia e Innovación (Spain) and 08667/PI/08 from Programa de Generación de Conocimiento Científico de Excelencia de la Fundación Séneca, Agencia de Ciencia y Tecnología de la Comunidad Autónoma de la Región de Murcia (II PCTRM 2007-10), and COST Action IS1104 “The EU in the new economic complex geography: models, tools and policy evaluation.”




