Fast Spectral Collocation Method for Solving Nonlinear Time-Delayed Burgers-Type Equations with Positive Power Terms
Abstract
Since the collocation method approximates ordinary differential equations, partial differential equations, and integral equations in physical space, it is very easy to implement and adapt to various problems, including variable coefficient and nonlinear differential equations. In this paper, we derive a Jacobi-Gauss-Lobatto collocation method (J-GL-C) to solve numerically nonlinear time-delayed Burgers-type equations. The proposed technique is implemented in two successive steps. In the first one, we apply (N − 1) nodes of the Jacobi-Gauss-Lobatto quadrature which depend upon the two general parameters (θ, ϑ > −1), and the resulting equations together with the two-point boundary conditions constitute a system of (N − 1) ordinary differential equations (ODEs) in time. In the second step, the implicit Runge-Kutta method of fourth order is applied to solve a system of (N − 1) ODEs of second order in time. We present numerical results which illustrate the accuracy and flexibility of these algorithms.
1. Introduction
Spectral methods have emerged as powerful techniques used in applied mathematics and scientific computing to numerically solve linear and nonlinear differential equations [1–4] and integral equations [5–7]. Also, they have become increasingly popular for solving fractional differential equations [8–10]. The main idea of spectral methods is to put the solution of the problem as a sum of certain basic functions and then to choose the coefficients in the sum in order to minimize the difference between the exact solution and the approximate one as well as possible. The choice of test functions leads to the three well-known types of spectral methods, namely, the Galerkin, tau, and collocation methods [11–14]. Spectral collocation method has an exponential convergence rate, which is very useful in providing highly accurate solutions to nonlinear differential equations even using a small number of grids.
The Jacobi polynomials satisfy the orthogonality condition on the interval [−1,1] with respect to the weight function (1 − x) θ(l + x) ϑ. There are many special cases of the Jacobi polynomials such as Gegenbauer, Legendre, Zernike, ultraspherical, and Chebyshev polynomials [15]. In recent decades, the use of Jacobi polynomials for solving differential equations has gained increasing popularity due to obtaining the solution in terms of the Jacobi parameters θ and ϑ (see, e.g., [16, 17]).
Time-delay partial differential equations are a type of differential equations in which the derivative of the unknown function at a certain time is given in terms of the values of the function at previous times. They have a wide range of applications in science and engineering such as physical, chemical, and biological sciences [18, 19]. Also, time-delayed nonlinear partial differential equations described the propagation and transport phenomena or population dynamics.
The solution of delay differential equations has been presented by many authors, but we briefly review some of them. In [20], Ghasemi and Kajani developed a numerical approach of time-varying delay systems using Chebyshev wavelets. Hybrid functions together with Legendre polynomials are investigated in [21–23] to obtain efficient numerical solution of delay systems. Sedaghat et al. [24] presented a numerical scheme based on Chebyshev polynomials to treat the delay differential equations of pantograph type. The authors in [25] proposed a Bernoulli operational matrix method for solving generalized pantograph equation. Recently, Ali et al. [26] implemented spectral Legendre approach for solving pantograph-type differential and integral equations with studying the error analysis of the method. More recently, the work of Trif [27] discussed the application of the Tau method based on operational matrix of Chebyshev polynomials for solving DDEs of pantograph-type.
Recently, the authors of [28] and [29] presented some new travelling wave solutions of Burgers equation with finite transport memory and the Korteweg-de Vries-Burgers equation, respectively. Pandey et al. [30] investigated Du Fort-Frankel finite difference approach for solving Burgers equation in finite domain. Meanwhile, in [31], Sun and Wu presented and applied an efficient numerical solution for the Burgers equation based on a difference scheme in an unbounded domain. More recently, a differential quadrature scheme for Burgers equations was proposed in [32]. The idea of commutative hypercomplex mathematics and the homotopy perturbation method were combined to investigate solutions of time-delayed Burgers equation by Rostamy and Karimi [33]. The Darboux transformation was described in [34] to determine the exact solutions to the Burgers equation. Caglar and Ucar [35] proposed the nonpolynomial cubic spline scheme to develop a numerical solution of Burgers equation. Regarding the two-dimensional Burgers equation, Wang and Zhao [36] presented a novel combination of two-dimensional Haar wavelet functions based on tensorial products for solving two-dimensional Burgers equation.
Time-delayed Burgers equation has a wide range of application in many areas of applied sciences, for example, forest fire, population growth models, and Neolithic transitions [37, 38]. The time-delayed Burgers-Fisher equation is a very important model to forest fire, population growth, Neolithic transitions, the interaction between the reaction mechanism, convection effect and diffusion transport, and so forth [37]. Fahmy et al. [39] used improved tanh function, variational iteration, and the Adomian decomposition methods to present some exact solutions and numerical solutions of the time-delayed Burgers equation. With the aid of a subsidiary high-order ODE, Zhang et al. [37] obtained the exact solutions of the generalized time-delayed Burgers-Fisher equation with positive fractional power terms. Jawad et al. [40] introduced the exact solution of time-delayed Burgers equation using complex tanh method. Moreover, (G′/G)-expansion method is applied by Kim and Sakthivel [41] to find the exact solutions of time-delayed Burgers equation.
The goal of this paper is to propose an orthogonal collocation scheme for solving three nonlinear time-delay partial differential equations based on Jacobi family in which the roots of the Jacobi orthogonal polynomials whose distributions can be tuned by two parameters θ and ϑ. Firstly, we apply the Jacobi-Gauss-Lobatto collocation (J-GL-C) method to the model equation for discretizing spatial derivatives, using (N − 1) nodes of the Jacobi-Gauss-Lobatto quadrature which depends upon the two general parameters (θ, ϑ > −1); these equations together with the two-point boundary conditions constitute system of (N − 1) ordinary differential equations (ODEs) in time. Secondly, the Runge-Kutta method of fourth order is investigated for the time integration of the resulting system of (N − 1) nonlinear second-order ODEs.
Indeed, the main advantage of the proposed technique is that the Legendre and Chebyshev collocation methods and other methods can be obtained as special cases from our proposed technique. Comparison of the results obtained by various choices of Jacobi parameters θ and ϑ reveals that the present method is very effective and convenient for all choices of θ and ϑ. Finally, the accuracy of the proposed method is showed by test problems. From the results, these algorithms are extremely efficient and accurate for solving nonlinear time-delayed Burgers′-type equations.
The rest of this paper is structured as follows. In the next section, some basic properties of Jacobi polynomials, which are required in our paper, are given. Section 3 is devoted to the development of Gauss-Lobatto collocation technique for a general form of time-delay partial differential equation based on the Jacobi polynomials, and in Section 4 the proposed method is applied to obtain some numerical results for three problems of time-delay partial differential equations with known exact solutions. Finally, a brief conclusion and some remarks are provided in Section 5.
2. Preliminaries
3. Jacobi Spectral Collocation Method
Remark 1. We can replace the Jacobi polynomials by the Legendre, Chebyshev of the first, second, third, and fourth kinds, or Gegenbauer polynomials and replace the nodes of Jacobi-Gauss-Lobatto quadrature by the Legendre-, Chebyshev-, or Gegenbauer-Gauss-Lobatto quadrature (cf. [42–45]), just by taking the special cases θ = ϑ = 0, θ = ϑ = −0.5, θ = −0.5, ϑ = 0.5, θ = 0.5, ϑ = −0.5, or θ = ϑ, respectively, in the resulting system of ordinary differential equations.
4. Numerical Results and Discussions
This section considers three numerical examples to demonstrate the accuracy and applicability of the proposed method in the present paper. Comparison of the results obtained by various choices of Jacobi parameters θ and ϑ reveals that the present method is very effective and convenient for all choices of θ and ϑ.
We consider the following three examples.
Example 2. As a first example, we consider the nonlinear time-delayed one-dimensional Burgers equation in the form
The exact solution [39] of (34) is
Maximum absolute errors of (34) subject to (35) and (36) are introduced in Table 1 using J-GL-C method with various choices of N, θ and ϑ, and −A = B = 10; this table indicates that the obtained results are very accurate for a small choice of N, while the absolute errors of problem (34) are presented in Table 2 for θ = ϑ = 1/2, λ1 = 0.01, τ = 0.5, and N = 12 with different values of (x, t) in the interval [0,100].
| N | A | B | θ | ϑ | ME | N | A | B | θ | ϑ | ME |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 2 | −10 | 10 | 0 | 0 | 2.59 × 10−7 | 2 | −10 | 10 | 0.5 | 0.5 | 2.59 × 10−7 |
| 4 | 2.70 × 10−11 | 4 | 2.31 × 10−11 | ||||||||
| 6 | 2.22 × 10−15 | 6 | 1.89 × 10−15 | ||||||||
| 8 | 1.11 × 10−16 | 8 | 1.11 × 10−16 | ||||||||
| 2 | −10 | 10 | −0.5 | −0.5 | 2.59 × 10−7 | 2 | −10 | 10 | −0.5 | 0.5 | 8.95 × 10−7 |
| 4 | 2.23 × 10−11 | 4 | 5.97 × 10−11 | ||||||||
| 6 | 3.22 × 10−15 | 6 | 3.77 × 10−15 | ||||||||
| 8 | 1.11 × 10−16 | 8 | 1.11 × 10−16 | ||||||||
| x | t | N | A | B | E | x | t | N | A | B | E |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0.1 | 12 | 0 | 100 | 3.33 × 10−16 | 0 | 0.2 | 12 | 0 | 100 | 7.77 × 10−16 |
| 10 | 5.55 × 10−17 | 10 | 5.55 × 10−17 | ||||||||
| 02 | 5.55 × 10−17 | 20 | 0 | ||||||||
| 30 | 5.55 × 10−17 | 30 | 5.55 × 10−17 | ||||||||
| 40 | 5.55 × 10−17 | 40 | 0 | ||||||||
| 50 | 0 | 50 | 5.55 × 10−17 | ||||||||
| 60 | 1.67 × 10−16 | 60 | 5.55 × 10−17 | ||||||||
| 70 | 0 | 70 | 5.55 × 10−17 | ||||||||
| 80 | 1.11 × 10−16 | 80 | 0 | ||||||||
| 90 | 1.67 × 10−16 | 90 | 0 | ||||||||
| 100 | 5.00 × 10−16 | 100 | 5.55 × 10−17 |
In Figure 1, we see that the approximate solution and the exact solution for t = 0.5 of problem (34) coincide with values of parameters listed in their caption. Moreover, the absolute error of problem (34) where θ = ϑ = −1/2 and N = 2 is displayed in Figure 2. In Figure 3, we plotted the approximate solution . This assertion shows that the obtained numerical results are accurate and compare favorably with the exact solution.
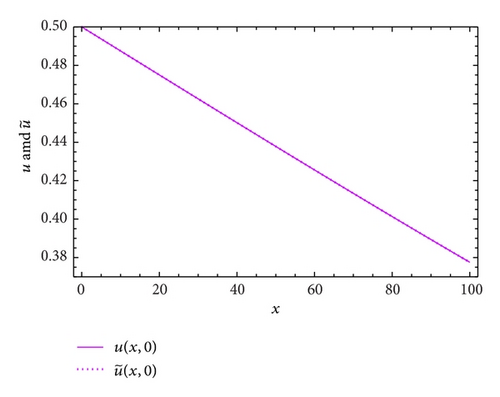
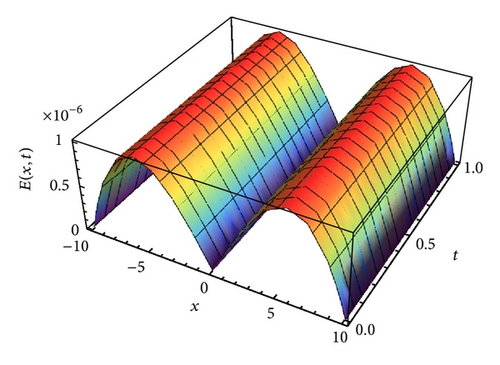
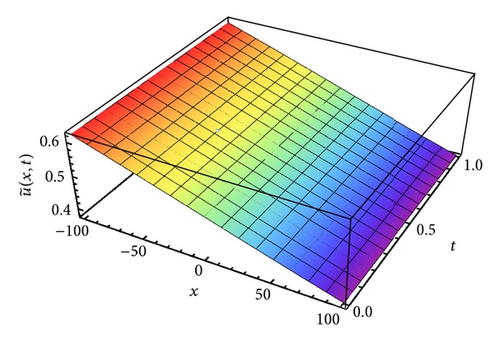
Example 3. Consider the nonlinear time-delayed one-dimensional generalized Burgers equation in the form
and the initial conditions
The exact solution [39] of (39) is
Table 3 lists the maximum absolute errors of (39) subject to (40) and (41) in [−10,10], using J-GL-C method for different values of N, θ, and ϑ. Moreover, in Tables 4 and 5, we evaluate the absolute errors of (39) for s = 3 and 5, respectively, with different values of (x, t) in the interval [−100,100].
| N | A | B | θ | ϑ | ME | N | A | B | θ | ϑ | ME |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 2 | −10 | 10 | 0 | 0 | 6.20 × 10−5 | 2 | −10 | 10 | 0.5 | 0.5 | 6.20 × 10−5 |
| 4 | 5.53 × 10−9 | 4 | 4.84 × 10−9 | ||||||||
| 6 | 5.89 × 10−13 | 6 | 4.86 × 10−13 | ||||||||
| 8 | 2.22 × 10−16 | 8 | 2.22 × 10−16 | ||||||||
| 2 | −10 | 10 | −0.5 | −0.5 | 6.20 × 10−5 | 2 | −10 | 10 | −0.5 | 0.5 | 5.202 × 10−5 |
| 4 | 6.45 × 10−9 | 4 | 4.24 × 10−9 | ||||||||
| 6 | 7.29 × 10−13 | 6 | 4.42 × 10−13 | ||||||||
| 8 | 3.33 × 10−16 | 8 | 1.11 × 10−16 | ||||||||
| x | t | N | A | B | E | x | t | N | A | B | E |
|---|---|---|---|---|---|---|---|---|---|---|---|
| −100 | 0.1 | 12 | −100 | 100 | 1.46 × 10−11 | −100 | 0.2 | 12 | −100 | 100 | 1.45 × 10−11 |
| −80 | 1.85 × 10−12 | −80 | 1.85 × 10−12 | ||||||||
| −60 | 1.66 × 10−12 | −60 | 1.16 × 10−12 | ||||||||
| −40 | 1.06 × 10−12 | −40 | 1.05 × 10−12 | ||||||||
| −20 | 8.93 × 10−13 | −20 | 8.92 × 10−13 | ||||||||
| 0 | 4.89 × 10−13 | 0 | 4.87 × 10−13 | ||||||||
| 20 | 7.77 × 10−15 | 20 | 8.55 × 10−15 | ||||||||
| 40 | 3.54 × 10−13 | 40 | 3.54 × 10−13 | ||||||||
| 60 | 4.50 × 10−13 | 60 | 4.50 × 10−13 | ||||||||
| 80 | 1.89 × 10−13 | 80 | 1.90 × 10−13 | ||||||||
| 100 | 5.83 × 10−13 | 100 | 5.81 × 10−13 |
| x | t | N | A | B | E | x | t | N | A | B | E |
|---|---|---|---|---|---|---|---|---|---|---|---|
| −100 | 0.1 | 12 | −100 | 100 | 2.13 × 10−12 | −100 | 0.2 | 12 | −100 | 100 | 2.13 × 10−12 |
| −80 | 3.24 × 10−13 | −80 | 3.20 × 10−13 | ||||||||
| −60 | 2.00 × 10−13 | −60 | 2.01 × 10−13 | ||||||||
| −40 | 5.94 × 10−13 | −40 | 5.92 × 10−13 | ||||||||
| −20 | 1.70 × 10−12 | −20 | 1.69 × 10−12 | ||||||||
| 0 | 2.13 × 10−12 | 0 | 2.13 × 10−12 | ||||||||
| 20 | 1.46 × 10−12 | 20 | 1.45 × 10−12 | ||||||||
| 40 | 2.66 × 10−13 | 40 | 2.64 × 10−13 | ||||||||
| 60 | 4.87 × 10−13 | 60 | 4.88 × 10−13 | ||||||||
| 80 | 1.13 × 10−13 | 80 | 1.08 × 10−13 | ||||||||
| 100 | 2.13 × 10−12 | 100 | 2.13 × 10−12 |
Figure 4 plots the approximate and the exact solutions at t = 0.5 of (39) with the special values θ = ϑ = −1/2, λ1 = 0.01, s = 2, and N = 12. Moreover, the absolute errors between the approximate and the exact solutions of (39) with θ = ϑ = 1/2, λ1 = 0.01, s = 3, and N = 8 are shown in Figure 5.
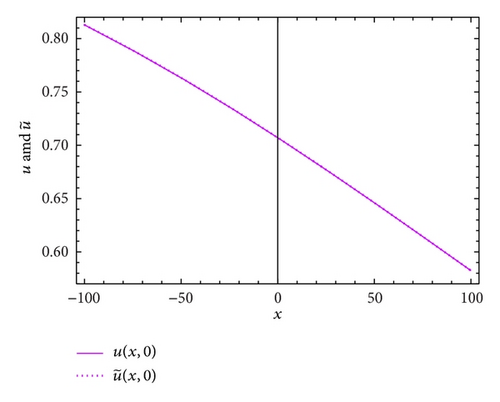
Example 4. Consider the nonlinear time-delayed Burgers-Fisher equation in the form
The exact solution [39] of (44) is
Maximum absolute errors of (44) subject to (45) and (46) are tabulated in Table 6 using J-GL-C method with various choices of N, θ, and ϑ, while the absolute errors of (44) are presented in Table 7 for θ = ϑ = 0 and N = 40 with different values of (x, t) in the interval [−5,5].
| N | A | B | θ | ϑ | ME | N | A | B | θ | ϑ | ME |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 8 | −10 | 10 | 0 | 0 | 2.25 × 10−3 | 8 | −10 | 10 | 0.5 | 0.5 | 1.92 × 10−3 |
| 20 | 6.10 × 10−7 | 20 | 5.16 × 10−7 | ||||||||
| 32 | 2.83 × 10−10 | 32 | 3.01 × 10−10 | ||||||||
| 8 | −10 | 10 | −0.5 | −0.5 | 2.73 × 10−3 | 8 | −10 | 10 | 0.5 | 0.5 | 3.09 × 10−3 |
| 20 | 7.70 × 10−7 | 20 | 8.81 × 10−7 | ||||||||
| 32 | 3.36 × 10−10 | 32 | 2.67 × 10−10 | ||||||||
| x | t | N | A | B | E | x | t | N | A | B | E |
|---|---|---|---|---|---|---|---|---|---|---|---|
| −5 | 0.1 | 12 | −5 | 5 | 4.16 × 10−12 | −5 | 0.2 | 12 | −5 | 5 | 1.66 × 10−12 |
| −4 | 1.84 × 10−13 | −4 | 6.58 × 10−13 | ||||||||
| −3 | 5.07 × 10−13 | −3 | 3.95 × 10−13 | ||||||||
| −2 | 3.32 × 10−13 | −2 | 5.74 × 10−13 | ||||||||
| −1 | 2.82 × 10−13 | −1 | 9.45 × 10−13 | ||||||||
| 0 | 3.59 × 10−13 | 0 | 3.07 × 10−13 | ||||||||
| 1 | 7.25 × 10−13 | 1 | 2.60 × 10−13 | ||||||||
| 2 | 1.01 × 10−12 | 2 | 3.42 × 10−13 | ||||||||
| 3 | 9.92 × 10−13 | 3 | 3.12 × 10−13 | ||||||||
| 4 | 6.08 × 10−14 | 4 | 7.46 × 10−13 | ||||||||
| 5 | 4.16 × 10−12 | 5 | 1.66 × 10−12 |
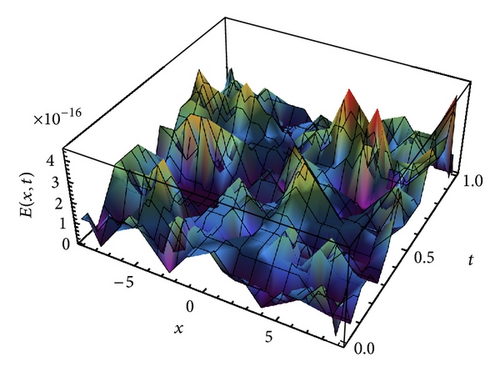
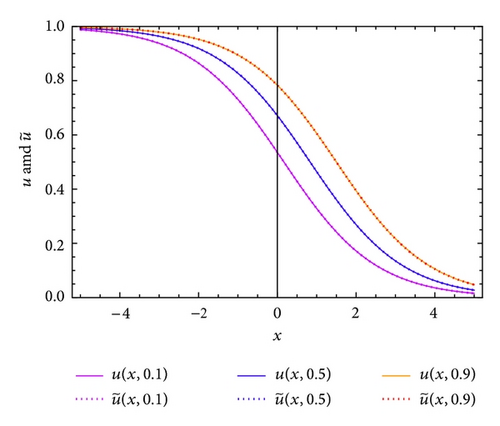
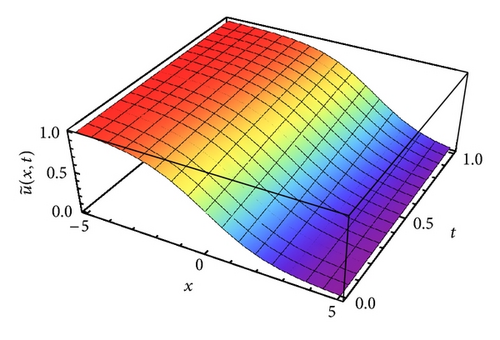
In Figure 6, we see that the approximate solution and the exact solution of (44) coincide for different values of t = 0, 0.5, and 0.9 and θ = ϑ = 0, λ1 = 0.01, τ = 0.5, and N = 40. The approximate solution of (44) with θ = ϑ = 0, λ1 = 0.01, τ = 0.5, and N = 40 is displayed in Figure 7, while the absolute error of (44) with θ = ϑ = 0, λ1 = 0.01, τ = 0.5, and N = 40 is displayed in Figure 8.

5. Conclusions and Future Works
We have constructed in this paper an efficient spectral-collocation algorithm for solving nonlinear time-delayed Burgers-type equations with positive power terms subject to initial and boundary conditions. The Jacobi-Gauss-Lobatto collocation methods based upon two general parameters, θ and ϑ, are developed and applied to the time-delayed Burgers-type equations for reformulating the problem to a system of second-order ordinary differential equations.
In fact, Jacobi-Gauss-Lobatto collocation method is slightly more complicated to implement than other orthogonal collocation methods but is more efficient and can be applied to a wider class of problems. We presented some advantages of the presented algorithm, as well as numerical results which demonstrate its accuracy and flexibility.
While the new algorithm presented in this paper only applied to a specific class of nonlinear time-delayed equations, it is very efficient and accurate whenever applicable. Moreover, high accuracy in long computational intervals and the stability of the proposed method encourage us to apply a similar scheme for the numerical solution of coupled nonlinear partial differential equations and other applied mathematics problems (see, e.g, [46–49] and references therein) in the future.




