Synchronization of Switched Complex Bipartite Neural Networks with Infinite Distributed Delays and Derivative Coupling
Abstract
A new model of switched complex bipartite neural network (SCBNN) with infinite distributed delays and derivative coupling is established. Using linear matrix inequality (LMI) approach, some synchronization criteria are proposed to ensure the synchronization between two SCBNNs by constructing effective controllers. Some numerical simulations are provided to illustrate the effectiveness of the theoretical results obtained in this paper.
1. Introduction
In recent years, neural networks have been intensively studied due to their potential applications in many different areas such as signal and image processing, content-addressable memory, optimization, and parallel computation [1–3]. Bidirectional associative memory (BAM) neural networks were first proposed by Kosko in [4, 5]. This class of networks has good applications in pattern recognition, solving optimization problems, and automatic control engineering. A large number of results on the dynamical behavior of BAM neural networks have been reported [6–9].
Switched systems, as an important kind of hybrid systems, have drawn considerable attention of researchers because of their theoretical significance and practical applications [10–12]. Switched systems are composed of a family of continuous-time or discrete-time subsystems and a rule that specifies the switching among them [13, 14]. Recently, the switched neural networks, whose individual subsystems are a set of neural networks, have found applications in the field of high speed signal processing, artificial intelligence, and biology, so there are many theoretical results about the switched neural networks [15–17].
Complex networks, which are a set of interconnected nodes with specific dynamics, have sparked the interest of many researchers from various fields of science and engineering such as the World Wide Web, electrical power grids, global economic markets, sensor networks; for example, see [18–20] and references therein. Bipartite networks are an important kind of complex networks, whose nodes can be divided into two disjoint nonempty sets such that every edge only connects a pair of nodes, which belong to different sets. Many real-world networks are naturally bipartite networks, such as the papers-scientists networks [21] and producer-consumer networks [22]. Recently, authors [23] have introduced a bipartite-graph complex dynamical network model that is only linearly coupled and has no delays. It is well known that time delays exist commonly in real-world systems. Therefore, many models of coupled networks with coupling delays are proposed, for example, constant single time delay [24], time-varying delays [25], and mix-time delays [26]. On the other hand, the coupled network often occurs in other forms, for example, nonlinearly coupled networks [27] and linearly derivative coupled networks [28]. In [29], a general model of bipartite dynamical network (BDN) with distributed delays and nonlinear derivative coupling was introduced. Synchronization of complex networks has been intensively investigated since they can be applied in power system control, secure communication, automatic control, chemical reaction, and so on [30–32]. The study of synchronization of coupled neural networks is an important step for both understanding brain science and designing coupled neural networks for practical use. Yu et al. [33] consider the synchronization of switched linearly coupled neural networks with constant delays, but the controllers are complex and changed with the switched rule. Synchronization of two coupled BDNs was investigated by adaptive method [29], but the controllers are complicated and the model does not include infinite distributed delays coupling and switching. Extending BAM neural networks to complex networks, we get complex bipartite dynamical networks (CBDNs). The dynamics of individual node in CBDNs is switched system and the switched coupling is considered; switched complex bipartite neural network (SCBNN) can be obtained. To the best of our knowledge, up to now, there is not any work that discusses the synchronization problem in SCBNN.
Motivated by the previous discussion, we first proposed a model of SCBNN, and then investigated the synchronization between two SCBNNs with infinite distributed delays and derivative coupling. Using adaptive controllers and linear matrix inequality (LMI) approach, some synchronization criteria are proposed to ensure the synchronization between two coupled SCBNNs. In our paper, the proposed controllers are simpler and do not change with the switched rule, which can be realize more easily.
The paper is organized as follows. In Section 2, a model of SCBNN with infinite distributed delays and derivative coupling is presented, and some hypotheses and lemmas are given too. In Section 3, several synchronization criteria on the SCBNNs are deduced. In Section 4, numerical examples are given to demonstrate the effectiveness of the proposed controller design methods in Section 3. Finally, conclusions are given in Section 5.
Notations. Throughout this paper, ρmax (·) and ρmin (·) denote the maximum eigenvalue and minimum eigenvalue of a real symmetric matrix, respectively. The notation * denotes the symmetric block.
2. Model Description, Assumptions, and Lemmas
-
(S1) There exist diagonal matrices and , such that
() -
∀x, y ∈ R and x ≠ y, i = 1,2, 3,4, j = 1,2, …, n, and k = 1,2.
-
(S2) There exist diagonal matrices and , such that
() -
∀x, y ∈ R and x ≠ y, i = 1,2, 3,4, j = 1,2, …, n, and k = 1,2.
-
(S3) τ(t), τ1(t), τ2(t), σ(t), σ1(t), and σ2(t) are differential functions with , , , , , and .
-
(S4) are real-value nonnegative continuous functions defined in [0, ∞) satisfying
()
Lemma 1 (see [34].)Given any real matrices Σ1, Σ2, and Σ3 of appropriate dimensions and a scalar ε > 0 such that , then the following inequality holds:
Lemma 2 (see [35].)Given a positive definite matrix P ∈ Rn×nand a symmetric matrix Q ∈ Rn×n, then
Lemma 3 (Schur complement). Given constant symmetric matrices Σ1, Σ2, and Σ3, where and , then if and only if
For convenience, let
3. Main Results
Theorem 4. Under assumptions (S1)–(S4), the two coupled SCBNNs (4) and (5) can be synchronized, if there exist positive constants, , n × n positive matrices P, Q, U, , , and n × n diagonal positive matrices W = diag (w1, w2, …, wn), , such that
Proof. For the error dynamical system (6), we design the following Lyapunov-Krasovskii function:
Meanwhile, by a similar process, the following inequality can be true:
By condition (17), we have
From Theorem 4, we can get the following corollary.
Corollary 5. Under assumptions (S1)–(S4), the two coupled CBDNs (1) and (38) can be synchronized, if there exist positive constants , n × n positive matrices P, Q, U, , , and n × n diagonal positive matrices W = diag (w1, w2, …, wn), , Mi, such that
Remark 6. From Corollary 5, we can easily get that the controllers in this paper are simpler than those of Theorem 1 in [29].
Remark 7. If the coupling matrix of the SCBNN is not a diffusive matrix satisfying the sum of every row being zero, we can still obtain the same result from the proof of Theorem 4.
Theorem 8 presents another sufficient condition to ascertain that the two networks (4) and (5) can be synchronized, using the following simple adaptive feedback controllers:
Let
Theorem 8. Under assumptions (S1)–(S4) and using the adaptive feedback controllers (41), the two coupled SCBNNs (4) and (5) can be synchronized, if there exist n × n positive matrices P, U,, and n × n diagonal positive matrices W = diag (w1, w2, …, wn), , Q, V, M, , , such that for r ∈ ℵ, the following matrix inequalities hold:
Proof. For the error dynamical system (43), we define the following Lyapunov-Krasovskii function:
4. Simulations
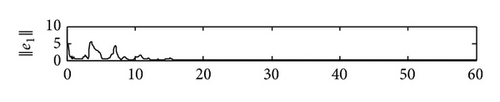
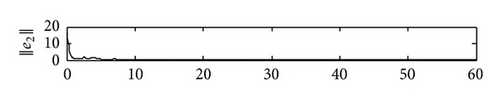

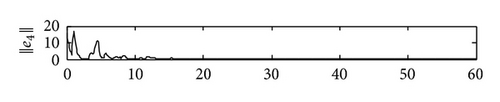


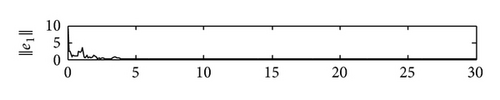
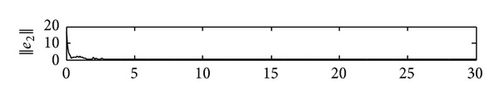
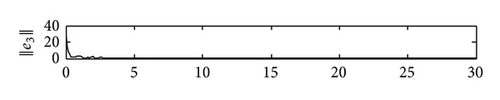
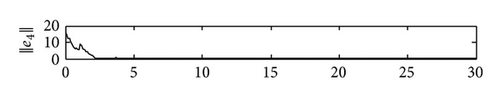

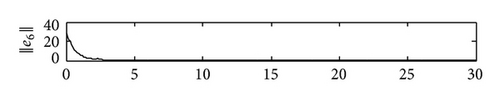
5. Conclusions
In this paper, we have proposed a general SCBNN with distributed delays and derivative coupling and investigated the synchronization problem in the two coupled SCBNNs. Using linear matrix inequality (LMI) approach and Barbǎlat lemma, we have deviated some useful synchronization criteria to ensure the synchronization of these two SCBNNs by constructing effective controllers. Compared with relative previous jobs, the controllers proposed by us are more simple and feasible. Some simulation results have been presented to demonstrate our theoretical results. In our future work, we will consider using pinning control to realize the synchronization of SCBNNs and identify the network topology of the unknown SCBNNs.
Acknowledgments
This research is supported by the National Natural Science Foundation of China under Grants nos. 61272530 and 11072059, the Natural Science Foundation of Jiangsu Province of China under Grants no. BK2012741, Specialized Research Fund for the Doctoral Program of Higher Education under Grants no. 20110092110017, and the National Social Science Fund of China under Grant no. 11BGL039.




