We consider the following class of three point boundary value problem y′′(t) + f(t, y) = 0, 0 < t < 1, y′(0) = 0, y(1) = δy(η), where δ > 0, 0 < η < 1, the source term f(t, y) is Lipschitz and continuous. We use monotone iterative technique in the presence of upper and lower solutions for both well-order and reverse order cases. Under some sufficient conditions, we prove some new existence results. We use examples and figures to demonstrate that monotone iterative method can efficiently be used for computation of solutions of nonlinear BVPs.

1. Introduction

In recent years, multipoint boundary value problems have been extensively studied by many authors ([1–5] and the references there in). Multipoint BVPs have lots of applications in various branches of science and engineering; for example, Webb [6] studied a second-order nonlinear boundary value problem subject to some nonlocal boundary conditions, which models a thermostat, and Zou et al. [7] studied the design of a large size bridge with multipoint supports.

It is well known that one of the most important tools for dealing with existence results for nonlinear problems is the method of upper and lower solutions. The method of upper and lower solutions has a long history and some of its ideas can be traced back to Picard [8]. Later, it was extensively studied by Dragoni [9].

Recently, there have been numerous results in the presence of an upper solution u₀ and a lower solution v₀ with u₀ ≥ v₀. But, in many cases, the upper and lower solutions may occur in the reversed order also, that is, u₀ ≤ v₀. Cabada et al. [10] considered the monotone iterative method for the following BVP:

(1)

with reversed ordered upper and lower solutions. So far, there have been some results in the presence of reverse ordered upper and lower solutions [10–13]. Xian et al. [14] considered the following second-order three point BVP:

(2)

where f(I × R, R), I = [0,1], 0 < η < 1, 0 < δ < 1. They used the fixed point index theory with non-well-ordered upper and lower solutions.

Recently, Li et al. [15] studied the existence and uniqueness of solutions of second-order three point BVP

(3)

with upper and lower solutions in the reversed order via the monotone iterative method in Banach space.

The present work proves some new existing results for three point BVPs. Our technique is based on Picard-type iterative scheme and is quite simple and efficient from computational point of view. We believe that it can be very well adapted for this type of problem. In this paper we consider the following three point BVP:

(4)

where f(I × R, R), I = [0,1], 0 < η < 1, δ > 0. We have allowed sup (∂f/∂y) to take both negative and positive values.

The paper is divided into 4 sections. In Section 2, we construct Green′s function and establish maximum and antimaximum principle. In Section 3, we generate monotone sequences by using results of Section 2 with upper and lower solutions as initial iterates ordered in one way or the other. We prove our final result of existence. In Section 4, we show that the monotone iterative scheme is a powerful technique. For that by using iterative scheme proposed in this paper we have computed the members of sequences in both cases (well-ordered and non-well-ordered case).

2. Preliminaries

2.1. Construction of Green′s Function

To investigate (4), we consider the following linear three point BVP:

(5)

where h ∈ C(I) and b is any constant. In this section, we construct the Green′s function. We divide it into two cases.

Case I (λ > 0). Let us assume that

(H₀) 0 < λ ≤ π²/4, , .

It is easy to see that (H₀) can be satisfied.

Lemma 1. Green′s function for the following linear three point BVP

(6)

is given by

(7)

and if H₀ holds then G(t, s) ≥ 0.

Proof. See proof of Lemma 2.1 in [15].

Lemma 2. When λ > 0, y ∈ C²(I) is a solution of boundary value problem (5) and is given by

(8)

Proof. See proof of Lemma 2.3 in [15].

Remark 3. Particulary y ∈ C²(I) is a solution of the boundary value problem (5) if and only if y ∈ C(I) is a solution of the integral equation

(9)

Case II (λ < 0). Assume that

λ < 0, , .

It is easy to see that can be satisfied.

Lemma 4. Green′s function for the following three point BVP

(10)

for λ < 0 is given by

(11)

where

and if

holds then G(t, s) ≤ 0.

Proof. Proof is same as given in Lemma 1.

Lemma 5. When λ < 0, y ∈ C²(I) is a solution of boundary value problem (5) and is given by

(12)

Proof. Proof is same as given in Lemma 2.

2.2. Maximum and Antimaximum Principle

Proposition 6 (antimaximum principle). Let 0 < λ ≤ π²/4, , , b ≥ 0, and h(t) ∈ C[0,1] is such that h(t) ≥ 0; then y(t) is nonpositive on I.

Proposition 7 (maximum principle). Let λ < 0, , , b ≥ 0 and h(t) ∈ C[0,1] is such that h(t) ≥ 0; then y(t) is nonnegative on I.

3. Three Point Nonlinear BVP

Based on maximum and antimaximum Principle we develop theory to solve the three point nonlinear BVP and divide it into the following two subsections.

3.1. Reverse Ordered Lower and Upper Solutions

Theorem 8. Let there exist v₀, u₀ in C²[0,1] such that u₀ ≤ v₀ and satisfies

(13)

(14)

If f : D → R is continuous on D : = {(t, y)∈[0,1] × R² : u₀ ≤ y ≤ v₀} and there exists M ≥ 0 such that for all (t, y), (t, w) ∈ D,

(15)

then the boundary value problem (5) has at least one solution in the region D. Further, if ∃ a constant λ such that M − λ ≤ 0 and (H₀) is satisfied, then the sequences {u_n} generated by

(16)

where F(t, u_n) = f(t, u_n) − λu_n, with initial iterate u₀ converge monotonically (non-decreasing) and uniformly towards a solution u(t) of (5). Similarly, using v₀ as an initial iterate leads to a nonincreasing sequences {v_n} converging to a solution v(t). Any solution z(t) in D must satisfy

(17)

Proof. From (13) and (16) (for n = 0)

(18)

Since h(t) ≥ 0 and b ≥ 0, by using Proposition 6, we have u₀ ≤ u₁.

In view of λ ≥ M, from (16) we get

(19)

and if u_n+1 ≥ u_n, then

(20)

Since u₀ ≤ u₁, then from (20) (for n = 0) and (16) (for n = 1), we get

(21)

From Proposition 6 we have u₁ ≤ u₂.

Now from (14) and (16) (for n = 0)

(22)

Thus, u₁ ≤ v₀ follows from Proposition 6.

Now assuming that u_n+1 ≥ u_n, u_n+1 ≤ v₀, we show that u_n+2 ≥ u_n+1 and u_n+2 ≤ v₀ for all n. From (16) (for n + 1) and (20), we get

(23)

and hence from Proposition 6 we have u_n+1 ≤ u_n+2.

From (16) (for n + 1) and (14) we get

(24)

Then, from Proposition 6, u_n+2 ≤ v₀ and hence we have

(25)

and starting with v₀ it is easy to get

(26)

Finally, we show that u_n ≤ v_n for all n. For this, by assuming u_n ≤ v_n, we show that u_n+1 ≤ v_n+1. From (16) it is easy to get

(27)

Hence, from Proposition 6, u_n+1 ≤ v_n+1. Thus we have

(28)

So, the sequences u_n and v_n are monotonically nondecreasing and nonincreasing, respectively, and are bounded by u₀ and v₀. Hence by Dini′s theorem they converge uniformly. Let u(t) = lim _n→∞ u_n(t) and v(t) = lim _n→∞ v_n(t).

Using Lemma 2, the solution u_n of (16) is given by

(29)

Then, by Lebesgue′s dominated convergence theorem, taking the limit as n approaches to ∞, we get

(30)

which is the solution of boundary value problem (5).

Any solution z(t) in D can play the role of u₀(t); hence, z(t) ≤ v(t) and similarly one concludes that z(t) ≥ u(t).

3.2. Well-Ordered Lower and Upper Solutions

Theorem 9. Let there exist v₀, u₀ in C²[0,1] such that u₀ ≥ v₀ and satisfies

(31)

If f : D₀ → R is continuous on D₀ : = {(t, y)∈[0,1] × R² : v₀ ≤ y ≤ u₀} and there exists M ≥ 0 such that for all

(32)

then the boundary value problem (5) has at least one solution in the region D₀. If ∃ a constant λ < 0, such that λ + M ≤ 0 and

is satisfied, then the sequences {u_n} generated by

(33)

where F(t, u_n) = f(t, u_n) − λu_n, with initial iterate u₀, converge monotonically (nonincreasing) and uniformly towards a solution

of (5). Similarly, using v₀ as an initial iterate leads to a nondecreasing sequences {v_n} converging to a solution

. Any solution

in D₀ must satisfy

(34)

Proof. Proof follows from the analysis of Theorem 8.

4. Numerical Illustration

To verify our results, we consider examples and show that there exists at least one value of λ ∈ ℝ∖{0} such that iterative scheme generates monotone sequences which converge to solutions of nonlinear problem. Thus, these examples validate sufficient conditions derived in this paper.

Example 10 (reverse order). Consider the boundary value problem

(35)

Here, f(t, y) = (e^y/32)−(1/64), δ = 2, η = 1/3. This problem has v₀ = 1 and u₀ = −1 as lower and upper solutions; that is, it is non-well-ordered case. The nonlinear term is Lipschitz in y and continuous for all value of y, and Lipschitz constants are M = e/32. For 0.0849463 ≤ λ ≤ π²/4 we can see that (H₀) will be true. To verify (H₀), in Figure 1 we plot inequalities assumed in (H₀). From Figures 2, 3, and 4, we plot members of monotone sequences u_n, v_n for different values of λ.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Plot of and .

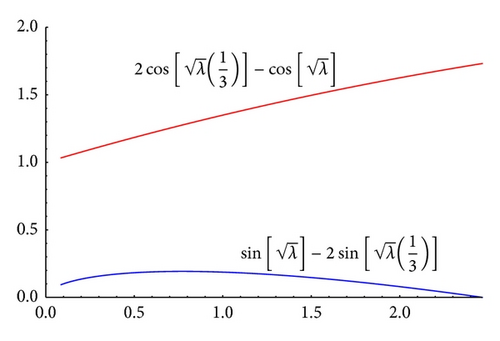
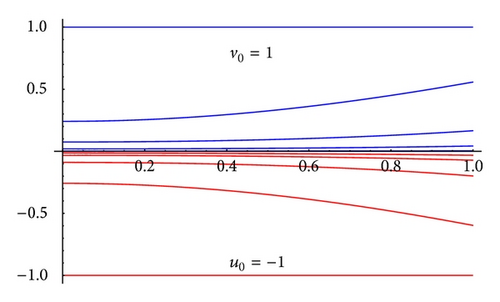
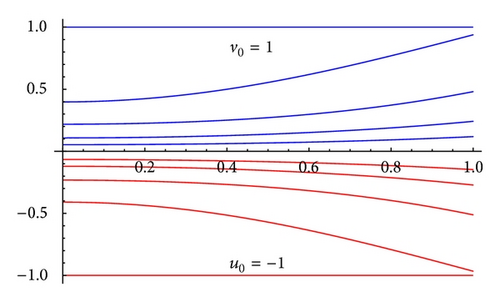
Example 11 (well order). Consider the boundary value problem

(36)

Here, f(t, y) = (1/32)[(e²/4)−(sint/4) − 2(y(t)) ³], δ = 1/3, η = 1/2. This problem has v₀ = −1 and u₀ = 1 as lower and upper solutions; that is, it is well-ordered case. The nonlinear term is Lipschitz in y and continuous for all value of y, and Lipschitz constants are M = 3/16. For λ ≤ −0.1875, we can see that

will be true. To verify

, in Figure 5 we plot inequalities assumed in

. From Figures 6, 7, and 8, we plot members of monotone sequences u_n, v_n for different values of λ.

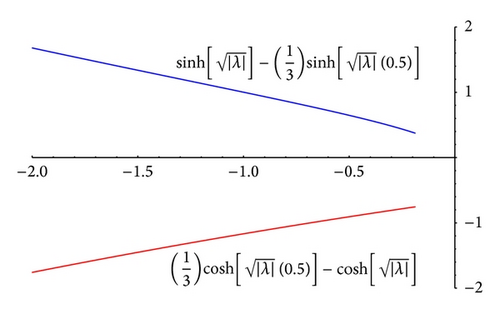
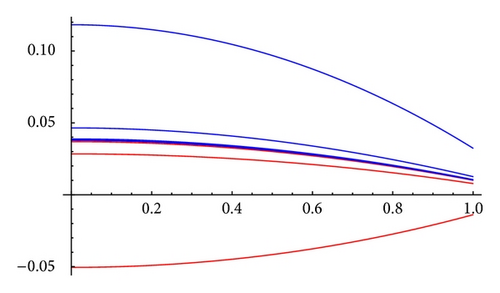
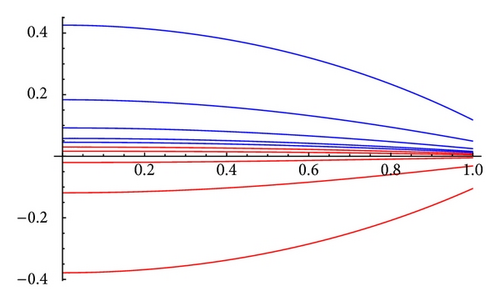
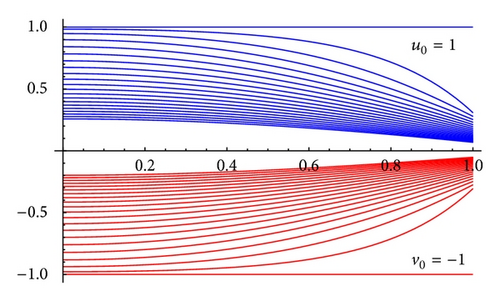
5. Conclusion

The monotone iterative technique coupled with upper and lower solutions is a powerful tool for computation of solutions of nonlinear three point boundary value problems. It proves the existence of solutions analytically and gives us a tool so that numerical solutions can also be computed and then some real-life problems, for example, bridge design problem, thermostat problem, and so forth, can be solved. We have plotted sequences for both λ > 0 and λ < 0. The plots are quite encouraging and will motivate researchers to explore further possibilities. Employing this technique, Mathematica/Maple/MATLAB user-friendly packages can be developed (see [16]).

Acknowledgment

This work is partially supported by Grant provided by UGC, New Delhi, India, File no. F.4-1/2006 (BSR)/7-203/2009(BSR).

References

1 Gupta C. P. and Trofimchuk S. I., Existence of a solution of a three-point boundary value problem and the spectral radius of a related linear operator, Nonlinear Analysis: Theory, Methods & Applications. (1998) 34, no. 4, 489–507, https://doi.org/10.1016/S0362-546X(97)00584-1, MR1635743.
10.1016/S0362-546X(97)00584-1
Web of Science® Google Scholar
2 Liu Y., Existence of three solutions to a non-homogeneous multi-point BVP of second order differential equations, Turkish Journal of Mathematics. (2011) 35, no. 1, 55–86, MR2809355.
Google Scholar
3 Ma R. and Castaneda N., Existence of solutions of nonlinear m-point boundary-value problems, Journal of Mathematical Analysis and Applications. (2001) 256, no. 2, 556–567, https://doi.org/10.1006/jmaa.2000.7320, MR1821757.
Google Scholar
4 Zhang Z. and Wang J., The upper and lower solution method for a class of singular nonlinear second order three-point boundary value problems, Journal of Computational and Applied Mathematics. (2002) 147, no. 1, 41–52, https://doi.org/10.1016/S0377-0427(02)00390-4, MR1931768.
10.1016/S0377-0427(02)00390-4
Google Scholar
5 Liu Y., A note on the existence of positive solutions of one-dimensional p-Laplacian boundary value problems, Applications of Mathematics. (2010) 55, no. 3, 241–264, https://doi.org/10.1007/s10492-010-0010-z, MR2657836.
Google Scholar
6 Webb J. R. L., Existence of positive solutions for a thermostat model, Nonlinear Analysis: Real World Applications. (2012) 13, no. 2, 923–938, https://doi.org/10.1016/j.nonrwa.2011.08.027, MR2846891.
Google Scholar
7 Zou Y., Hu Q., and Zhang R., On numerical studies of multi-point boundary value problem and its fold bifurcation, Applied Mathematics and Computation. (2007) 185, no. 1, 527–537, https://doi.org/10.1016/j.amc.2006.07.064, MR2297823.
Web of Science® Google Scholar
8 Picard E., Sur lapplication des metodes dapproximations succesives a letude de certains equations differentielles ordinaires, Journal de Mathmatiques Pures et Appliques. (1893) 9, 217–271.
Google Scholar
9 Dragoni G. S., II problema dei valori ai limiti studiato in grande per le equazioni differenziali del secondo ordine, Mathematische Annalen. (1931) 105, no. 1, 133–143, https://doi.org/10.1007/BF01455811, MR1512707.
Google Scholar
10 Cabada A., Habets P., and Lois S., Monotone method for the Neumann problem with lower and upper solutions in the reverse order, Applied Mathematics and Computation. (2001) 117, no. 1, 1–14, https://doi.org/10.1016/S0096-3003(99)00149-6, MR1801398.
10.1016/S0096-3003(99)00149-6
Web of Science® Google Scholar
11 Omari P. and Trombetta M., Remarks on the lower and upper solutions method for second- and third-order periodic boundary value problems, Applied Mathematics and Computation. (1992) 50, no. 1, 1–21, https://doi.org/10.1016/0096-3003(92)90007-N, MR1164490.
Google Scholar
12 Verma A. K., The monotone iterative method and zeros of Bessel functions for nonlinear singular derivative dependent BVP in the presence of upper and lower solutions, Nonlinear Analysis: Theory, Methods & Applications. (2011) 74, no. 14, 4709–4717, https://doi.org/10.1016/j.na.2011.04.037, MR2810710.
Google Scholar
13 Cherpion M., de Coster C., and Habets P., A constructive monotone iterative method for second-order BVP in the presence of lower and upper solutions, Applied Mathematics and Computation. (2001) 123, no. 1, 75–91, https://doi.org/10.1016/S0096-3003(00)00058-8, MR1846713.
10.1016/S0096-3003(00)00058-8
Google Scholar
14 Xian X., O′Regan D., and Jingxian S., Multiplicity results for three-point boundary value problems with a non-well-ordered upper and lower solution condition, Mathematical and Computer Modelling. (2007) 45, no. 1-2, 189–200, https://doi.org/10.1016/j.mcm.2006.05.003, MR2273449.
Google Scholar
15 Li F., Jia M., Liu X., Li C., and Li G., Existence and uniqueness of solutions of second-order three-point boundary value problems with upper and lower solutions in the reversed order, Nonlinear Analysis: Theory, Methods & Applications. (2008) 68, no. 8, 2381–2388, https://doi.org/10.1016/j.na.2007.01.065, MR2398658.
Google Scholar
16 Cabada A., Cid J., and Maquez-Villamarin B., Computation of Green’s functions for boundary value problems with Mathematica, Applied Mathematics and Computation. (2012) 219, no. 4, 1919–1936, https://doi.org/10.1016/j.amc.2012.08.035, MR2983897.
Google Scholar

Citing Literature

All articles

Picard Type Iterative Scheme with Initial Iterates in Reverse Order for a Class of Nonlinear Three Point BVPs

Abstract

1. Introduction

2. Preliminaries

2.1. Construction of Green′s Function

2.2. Maximum and Antimaximum Principle

3. Three Point Nonlinear BVP

3.1. Reverse Ordered Lower and Upper Solutions

3.2. Well-Ordered Lower and Upper Solutions

4. Numerical Illustration

5. Conclusion

Acknowledgment

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Picard Type Iterative Scheme with Initial Iterates in Reverse Order for a Class of Nonlinear Three Point BVPs

Abstract

1. Introduction

2. Preliminaries

2.1. Construction of Green′s Function

2.2. Maximum and Antimaximum Principle

3. Three Point Nonlinear BVP

3.1. Reverse Ordered Lower and Upper Solutions

3.2. Well-Ordered Lower and Upper Solutions

4. Numerical Illustration

5. Conclusion

Acknowledgment

References

Citing Literature

Figures

References

Related

Information