Volume 2013, Issue 1 715756

Research Article

Open Access

New Spectral Second Kind Chebyshev Wavelets Algorithm for Solving Linear and Nonlinear Second-Order Differential Equations Involving Singular and Bratu Type Equations

W. M. Abd-Elhameed,

W. M. Abd-Elhameed

Department of Mathematics, Faculty of Science, King Abdulaziz University, Jeddah, Saudi Arabia kau.edu.sa

Department of Mathematics, Faculty of Science, Cairo University, Giza 12613, Egypt cu.edu.eg

Search for more papers by this author

E. H. Doha,

E. H. Doha

Department of Mathematics, Faculty of Science, Cairo University, Giza 12613, Egypt cu.edu.eg

Search for more papers by this author

Y. H. Youssri,

Corresponding Author

Y. H. Youssri

[email protected]

Department of Mathematics, Faculty of Science, Cairo University, Giza 12613, Egypt cu.edu.eg

Search for more papers by this author

W. M. Abd-Elhameed,

W. M. Abd-Elhameed

Department of Mathematics, Faculty of Science, King Abdulaziz University, Jeddah, Saudi Arabia kau.edu.sa

Department of Mathematics, Faculty of Science, Cairo University, Giza 12613, Egypt cu.edu.eg

Search for more papers by this author

E. H. Doha,

E. H. Doha

Department of Mathematics, Faculty of Science, Cairo University, Giza 12613, Egypt cu.edu.eg

Search for more papers by this author

Y. H. Youssri,

Corresponding Author

Y. H. Youssri

[email protected]

Department of Mathematics, Faculty of Science, Cairo University, Giza 12613, Egypt cu.edu.eg

Search for more papers by this author

First published: 02 December 2013

https://doi.org/10.1155/2013/715756

Citations: 17

Academic Editor: Turgut Öziş

Share a link

Email
Wechat
Bluesky

Abstract

A new spectral algorithm based on shifted second kind Chebyshev wavelets operational matrices of derivatives is introduced and used for solving linear and nonlinear second-order two-point boundary value problems. The main idea for obtaining spectral numerical solutions for these equations is essentially developed by reducing the linear or nonlinear equations with their initial and/or boundary conditions to a system of linear or nonlinear algebraic equations in the unknown expansion coefficients. Convergence analysis and some efficient specific illustrative examples including singular and Bratu type equations are considered to demonstrate the validity and the applicability of the method. Numerical results obtained are compared favorably with the analytical known solutions.

1. Introduction

Spectral methods are one of the principal methods of discretization for the numerical solution of differential equations. The main advantage of these methods lies in their accuracy for a given number of unknowns (see, e.g., [1–3]). For smooth problems in simple geometries, they offer exponential rates of convergence/spectral accuracy. In contrast, finite difference and finite-element methods yield only algebraic convergence rates. The three most widely used spectral versions are the Galerkin, collocation, and tau methods. Collocation methods have become increasingly popular for solving differential equations, also they are very useful in providing highly accurate solutions to nonlinear differential equations (see, e.g., [4, 5]).

The subject of wavelets has recently drawn a great deal of attention from mathematical scientists in various disciplines. It is creating a common link between mathematicians, physicists, and electrical engineers. Wavelets theory is a relatively new and an emerging area in mathematical research. It has been applied to a wide range of engineering disciplines; particularly, wavelets are very successfully used in signal analysis for wave form representation and segmentations, time frequency analysis, and fast algorithms for easy implementation. Wavelets permit the accurate representation of a variety of functions and operators. Moreover, wavelets establish a connection with fast numerical algorithms (see [6, 7]).

The subject of nonlinear differential equations is a well-established part of mathematics, and its systematic development goes back to the early days of the development of calculus. Many recent advances in mathematics, paralleled by a renewed and flourishing interaction between mathematics, sciences, and engineering, have again shown that many phenomena in applied sciences, modelled by differential equations, will yield some mathematical explanation of these phenomena [8–10].

Even-order differential equations have been extensively discussed by a large number of authors due to their great importance in various applications in many fields. For example, in the sequence of papers [1, 2, 11], the Galerkin method is applied for handling these problems. They constructed suitable basis functions which satisfy the boundary conditions of the given differential equation. For this purpose, they used compact combinations of various orthogonal polynomials. The suggested algorithms in these papers are suitable for handling one- and two-dimensional linear high even-order boundary value problems.

In this paper, we aim to give some algorithms for handling both linear and nonlinear second-order boundary value problems based on introducing a new matrix of derivatives, then applying Petrov-Galerkin method on linear equations and collocation method on nonlinear equations. High accurate spectral wavelets solutions are achieved with a small number of retained modes compared with the usual spectral methods, also we can handle singular differential equations with discontinuous variable coefficients.

Among the second-order boundary value problems is the one-dimensional Bratu problem which has a long history. Bratu’s own paper appeared in 1914 [12]; generalizations are sometimes called the Liouville-Gelfand or Liouville-Gelfand-Bratu problem in honor of Gel’fand [13] and the nineteenth century work of the great French mathematician Liouville. In recent years, it has been a popular testbed for numerical and perturbation methods [14–16].

Simplification of the solid fuel ignition model in thermal combustion theory yields an elliptic nonlinear partial differential equation, namely, the Bratu problem. Also due to its use in a large variety of applications, many authors have contributed to the study of such problem. Some applications of Bratu problem are the model of thermal reaction process, the Chandrasekhar model of the expansion of the Universe, chemical reaction theory, nanotechnology, and radiative heat transfer (see [17–21]).

The application of Legendre wavelets for solving differential and integral equations is thoroughly considered by many authors (see, [22–26]). Also, Chebyshev wavelets are used for solving some differential, fractional and integral equations (see [5, 27–31]).

In [32, 33], a cosine and sine (CAS) wavelets operational matrix of fractional order integration has been derived and used to solve integrodifferential equations of fractional order.

One approach for solving differential equations is based on converting the differential equations into integral equations through integration, approximating various signals involved in the equation by truncated orthogonal series, and using the operational matrix of integration, to eliminate the integral operations.

Special attentions have been given to applications of block pulse functions [34], Legendre polynomials [35], Chebyshev polynomials [36], Haar wavelets [37], Legendre wavelets [24, 25, 38], and Chebyshev wavelets [27]. Another approach is based on using operational matrix of derivatives in order to reduce the problem into solving a system of algebraic equations (see [23]).

The main aim of this paper is to develop a new spectral algorithm for solving second-order two-point boundary value problems based on shifted second kind Chebyshev wavelets operational matrix of derivatives. The method reduces the differential equation with its initial and/or boundary conditions to a system of algebraic equations in the unknown expansion coefficients. Large systems of algebraic equations may lead to greater computational complexity and large storage requirements. However, the second kind Chebyshev wavelets are structurally sparse; this reduces drastically the computational complexity of solving the resulting algebraic system.

The structure of the paper is as follows. In Section 2, we give some relevant properties of second kind Chebyshev polynomials and their shifted forms. In Section 3, we develop a new shifted second kind Chebyshev wavelets operational matrices of derivatives (SCWOMD); also we ascertain the convergence analysis of the proposed algorithm. As an application of SCWOMD, numerical solutions of second-order linear and nonlinear initial value problems or two-point boundary value problems are implemented and presented in Section 4. In Section 5, some numerical examples are presented to show the efficiency and the applicability of the presented algorithm. Some concluding remarks are given in Section 6.

2. Some Properties of Second Kind Chebyshev Polynomials and Their Shifted Forms

In the present section, we discuss some relevant properties of the second kind Chebyshev polynomials and their shifted forms.

2.1. Second Kind Chebyshev Polynomials

It is well known that the second kind Chebyshev polynomials are defined on [−1,1] by

(1)

These polynomials are orthogonal on [−1,1]; that is,

(2)

The following properties of second kind Chebyshev polynomials (see, e.g., [39]) are of fundamental importance in the sequel. They are eigenfunctions of the following singular Sturm-Liouville equation:

(3)

where D ≡ d/dx and may be generated by using the recurrence relation

(4)

starting from U₀(x) = 1 and U₁(x) = 2x, or from Rodrigues formula

(5)

The following theorem is needed hereafter.

Theorem 1. The first derivative of second kind Chebyshev polynomials is given by

(6)

For a proof of Theorem 1, see [39].

2.2. Shifted Second Kind Chebyshev Polynomials

The shifted second kind Chebyshev polynomials are defined on [0,1] by

. All results of second kind Chebyshev polynomials can be easily transformed to give the corresponding results for their shifted forms. The orthogonality relation with respect to the weight function

is given by

(7)

The first derivative of

is given in the following corollary.

Corollary 2. The first derivative of the shifted second kind Chebyshev polynomial is given by

(8)

3. Shifted Second Kind Chebyshev Operational Matrix of Derivatives

Wavelets constitute of a family of functions constructed from dilation and translation of single function called the mother wavelet. When the dilation parameter a and the translation parameter b vary continuously, then we have the following family of continuous wavelets:

(9)

Second kind Chebyshev wavelets ψ_nm(t) = ψ(k, n, m, t) have four arguments: k, n can assume any positive integer, m is the order of second kind Chebyshev polynomials, and t is the normalized time. They are defined on the interval [0,1] by

(10)

3.1. Function Approximation

A function f(t) defined over [0,1] may be expanded in terms of second kind Chebyshev wavelets as

(11)

where

(12)

and

. If the infinite series is truncated, then f(t) can be approximated as

(13)

where C and Ψ(t) are 2^k(M + 1) × 1 matrices defined by

(14)

(15)

3.2. Convergence Analysis

We state and prove a theorem ascertaining that the second kind Chebyshev wavelet expansion of a function f(x), with bounded second derivative, converges uniformly to f(x).

Theorem 3. A function , with |f^′′(x)| ⩽ L, can be expanded as an infinite sum of Chebyshev wavelets, and the series converges uniformly to f(x). Explicitly, the expansion coefficients in (12) satisfy the following inequality:

(16)

Proof. From (12), it follows that

(17)

If we set 2^kx − n = cos θ in (17), then we get

(18)

which gives after integration by parts two times

(19)

where

(20)

Therefore, we have

(21)

Since n ⩽ 2^k − 1, we have

(22)

and this completes the proof of Theorem 3.

A shifted second kind Chebyshev wavelets operational matrix of the first derivative is stated and proved in the following theorem.

Theorem 4. Let Ψ(t) be the second kind Chebyshev wavelets vector defined in (15). Then, the first derivative of the vector Ψ(t) can be expressed as

(23)

where D is 2^k(M + 1) square operational matrix of derivative and is defined by

(24)

in which F is an (M + 1) square matrix whose (r, s)th element is defined by

(25)

Proof. If we make use of the shifted second kind Chebyshev polynomials, then the rth element of the vector Ψ(t) defined in (15) can be written in the following form:

(26)

where r = n(M + 1) + (m + 1), m = 0,1, …, M, n = 0,1, …, (2^k − 1), and

(27)

If we differentiate (26) with respect to t, then we get

(28)

It is to be noted here that the R.H.S. of (28) is zero outside the interval [n/2^k, (n + 1)/2^k]; hence, its second kind Chebyshev wavelets expansion only has those elements in Ψ(t) that are nonzero in the interval [n/2^k, (n + 1)/2^k]; that is, Ψ_i(t), i = n(M + 1) + 1, n(M + 1) + 2, …, n(M + 1) + M + 1, and as a consequence, this enables one to expand (dΨ_r(t)/dt) in terms of shifted second kind Chebyshev wavelets Ψ_i(t), i = n(M + 1) + 1, n(M + 1) + 2, …, n(M + 1) + M + 1, in the form

(29)

and accordingly (28) implies that the operational matrix D is a block matrix defined as in (24). Moreover, we have

(30)

and this implies that

(31)

Consequently, the elements of the first row of matrix F defined in (24) are zeros. Now and with the aid of Corollary 2, the first derivative of Ψ_r(t) may be expressed in the form

(32)

Expanding this equation in terms of second kind Chebyshev wavelets basis, we get

(33)

so if F_r,s are chosen as

(34)

then (23) is obtained, and the proof of the theorem is completed.

Corollary 5. The operational matrix for the nth derivative can be obtained from

(35)

where Dⁿ is the nth power of matrix D.

4. Second-Order Two-Point Boundary Value Problems

In this section, we are interested in solving linear and nonlinear two-point boundary value problems subject to homogenous or nonhomogenous initial or boundary conditions based on the wavelets operational matrices constructed in Section 3.

4.1. Linear Second-Order Two-Point Boundary Value Problems

Consider the linear second-order differential equation

(36)

subject to the initial conditions

(37)

or the boundary conditions

(38)

or the most general mixed boundary conditions

(39)

If we approximate y(x), f₁(x), f₂(x), and g(x) in terms of the second kind Chebyshev wavelets basis, then one can write

(40)

where C^T,

, and G^T are defined similarly as in (14). Relations (23) and (35) enable one to approximate y^′(x) and y^′′(x) as

(41)

Now, substitution of relations (40) and (41) into (36) enables us to define the residual, R(x), of this equation as

(42)

and application of the Petrov-Galerkin method (see [40]) yields the following (2^k(M + 1) − 2) linear equations in the unknown expansion coefficients, c_nm; namely,

(43)

Moreover, the initial conditions (37), the boundary conditions (38), and the mixed boundary conditions (39) lead, respectively, to the following equations:

(44)

(45)

(46)

Thus, (43) with the two equations of (44) or (45) or (46) generates 2^k(M + 1) a set of linear equations which can be solved for the unknown components of the vector C, and hence an approximate spectral wavelets solution to y(x) given in (40) can be obtained.

4.2. Nonlinear Second-Order Two-Point Boundary Value Problems

Consider the nonlinear differential equation

(47)

subject to the initial conditions

(48)

or the boundary conditions

(49)

or the most general mixed boundary conditions

(50)

If we follow the same procedure of Section 4.1, approximate y(x) as in (40) and make use of (23) and (35), then we obtain

(51)

To find an approximate solution to y(x), we compute (51) at the first 2^k(M + 1) − 2 roots of . These equations with (44) or (45) or (46) generate 2^k(M + 1) nonlinear equations in the expansion coefficients, c_nm, which can be solved with the aid of Newton’s iterative method.

5. Numerical Results and Discussions

In this section, the presented algorithms in Section 4 are applied to solve linear and nonlinear second-order initial and boundary value problems as well as Bratu’s equations. Some examples subject to different initial, boundary, and mixed boundary conditions are considered to illustrate the efficiency and the applicability of the proposed algorithms. All computations are performed by using Mathematica 8.

Example 1. Consider the following linear second-order boundary value problem:

(52)

with the exact solution y(x) = (1 − x)cos x.

In Table 1, the maximum absolute error E is listed for various values of k and M.

Table 1. Maximum absolute error E for Example 1.

k	M	E	k	M	E
	3	2.28 · 10⁻³		2	9.23 · 10⁻⁶
0	4	6.32 · 10⁻⁵	1	3	8.62 · 10⁻⁸
	5	6.23 · 10⁻⁶		4	1.07 · 10⁻⁹

Example 2. Consider the following linear second-order boundary value problem:

(53)

subject to the mixed boundary conditions

(54)

with the exact solution y(x) = cos x.

In Table 2, the maximum absolute error E is listed for various values of k and M.

Table 2. Maximum absolute error E for Example 2.

k	M	E	k	M	E
	3	2.52 · 10⁻⁵		2	4.90 · 10⁻⁸
0	4	2.11 · 10⁻⁶	1	3	2.55 · 10⁻⁹
	5	9.01 · 10⁻⁸		4	3.50 · 10⁻¹⁰

Example 3. Consider the following nonlinear initial value problem (see [41]):

(55)

with the exact solution y(x) = (x²/8) − 1.

We solve (55) using the algorithm described in Section 4.2 for the case corresponds to M = 2, k = 0 to obtain an approximate solution of y(x). First, if we make use of (24) and (35), then the two operational matrices D and D² are given, respectively, by

(56)

Moreover, Ψ(x) can be evaluated to give

(57)

If we set

(58)

then (55) takes the form

(59)

which is equivalent to

(60)

We only need to satisfy this equation at the first root of

, that is, at

, to get

(61)

Furthermore, the use of initial conditions in (55) leads to the two equations

(62)

The solution of the nonlinear system of (61)-(62) gives

(63)

and consequently

(64)

which is the exact solution.

Example 4. Consider the following nonlinear second-order boundary value problem:

(65)

with the exact solution y(x) = cosh x.

In Table 3, we list the maximum absolute error E, for various values of k and M.

Table 3. Maximum absolute error E for Example 4.

k	M	E	k	M	E
0	3	5.69 · 10⁻⁴	1	2	1.12 · 10⁻⁶
0	4	1.35 · 10⁻⁵	1	3	1.97 · 10⁻⁸

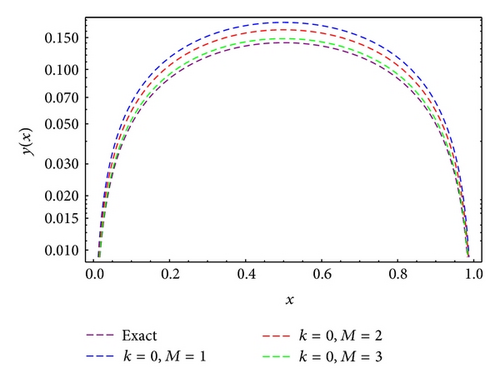
Example 5. Consider the following linear singular initial value problem (see [23]):

(66)

where

(67)

and g(x) is chosen such that the exact solution of (66) is y(x) = e^xsinx/(1 + x²). We apply the algorithm described in Section 4.1 with k = 2. In Table 4, we list the maximum absolute error for various values of M, while in Figure 1, the exact solution is compared with the three numerical solutions corresponding to k = 2, M = 2, k = 2, M = 4, k = 2, and M = 6 and also in Table 5 we give a comparison between the error obtained in [23] and the present method, k = 2, M = 8.

Table 4. Maximum absolute error E for Example 5.

M	E	M	E
2	2.98 · 10⁻⁴	6	1.85 · 10⁻¹⁰
4	1.70 · 10⁻⁵	8	9.12 · 10⁻¹¹

Table 5. Comparison between different errors for Example 5.

x	0.2	0.4	0.6	0.8
Legendre Wavelets [23]	4.30 · 10⁻¹²	1.24 · 10⁻¹¹	2.97 · 10⁻¹²	4.35 · 10⁻¹²
SCWOMD	6.47 · 10⁻¹³	1.21 · 10⁻¹²	1.74 · 10⁻¹²	2.32 · 10⁻¹²

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Numerical and exact solutions of Example 5.

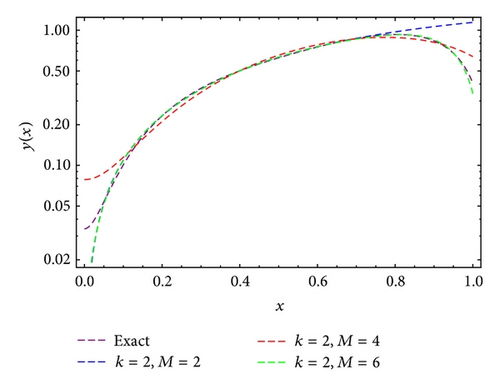
Example 6. Consider the following Bratu equation (see [17–20]):

(68)

with the analytical solution

(69)

where θ is the solution of the nonlinear equation

. The presented algorithm in Section 4.2 is applied to numerically solve (68), for the three cases corresponding to λ = 1, 2 and 3.51 which yield θ = 1.51716, 2.35755, and 4.66781, respectively. In Table 6, the maximum absolute error E is listed for k = 0 and various values of M, while in Table 7, we give a comparison between the best errors obtained by our method and some other numerical methods used to solve Example 6. This table shows that our method is more accurate if compared with the methods developed in [17–20]. In addition, Figure 2 illustrates a comparison between different solutions obtained by our algorithm in case of λ = 1, k = 0, and M = 1,2, 3.

Table 6. Maximum absolute error E for Example 6.

M	λ	E	λ	E	λ	E
10	1	2.162 · 10⁻⁷	2	2.758 · 10⁻⁵	3.51	7.658 · 10⁻⁴
12		4.453 · 10⁻⁹		8.082 · 10⁻⁶		8.665 · 10⁻⁵
14		8.461 · 10⁻¹¹		1.461 · 10⁻⁹		2.384 · 10⁻⁸
16		1.546 · 10⁻¹²		5.342 · 10⁻¹⁰		6.587 · 10⁻⁹
18		2.782 · 10⁻¹⁴		1.644 · 10⁻¹¹		2.387 · 10⁻¹⁰
20		7.216 · 10⁻¹⁶		4.024 · 10⁻¹²		1.058 · 10⁻¹⁰

Table 7. Comparison between the best errors for Example 6 for k = 0.

SCWOMD	Error in [17]	Error in [18]	Error in [19]	Error in [20]
7.22 · 10⁻¹⁶	1.02 · 10⁻⁶	8.89 · 10⁻⁶	1.35 · 10⁻⁵	3.01 · 10⁻³

Remark 6. It is worth noting here that the obtained numerical results in the previous six solved examples are very accurate, although the number of retained modes in the spectral expansion is very few, and again the numerical results are compared favorably with the known analytical solutions.

6. Concluding Remarks

In this paper, an algorithm for obtaining a numerical spectral solution for second-order linear and nonlinear boundary value problems is discussed. The derivation of this algorithm is essentially based on constructing the shifted second kind Chebyshev wavelets operational matrix of differentiation. One of the main advantages of the presented algorithm is its availability for application on both linear and nonlinear second-order boundary value problems including some singular equations and also Bratu type equations. Another advantage of the developed algorithm is that high accurate approximate solutions are achieved using a small number of the second kind Chebyshev wavelets. The obtained numerical results are compared favorably with the analytical ones.

Acknowledgments

This paper was funded by the Deanship of Scientific Research (DSR), King Abdulaziz University, Jeddah. The authors, therefore, acknowledge with thanks DSR technical and financial support. Also, they would like to thank the referee for his valuable comments and suggestions which improved the paper into its present form.

References

1 Doha E. H. and Abd-Elhameed W. M., Efficient spectral-Galerkin algorithms for direct solution of second-order equations using ultraspherical polynomials, SIAM Journal on Scientific Computing. (2002) 24, no. 2, 548–571, https://doi.org/10.1137/S1064827500378933, MR1951055, ZBL1020.65088.
10.1137/S1064827500378933
Web of Science® Google Scholar
2 Doha E. H., Abd-Elhameed W. M., and Bassuony M. A., New algorithms for solving high even-order differential equations using third and fourth Chebyshev-Galerkin methods, Journal of Computational Physics. (2013) 236, 563–579, https://doi.org/10.1016/j.jcp.2012.11.009, MR3020070.
10.1016/j.jcp.2012.11.009
Web of Science® Google Scholar
3 Abd-Elhameed W. M., Doha E. H., and Youssri Y. H., Efficient spectral-Petrov-Galerkin methods for third- and fifth-order differential equations using general parameters generalized Jacobi polynomials, Quaestiones Mathematicae. (2013) 36, no. 1, 15–38, https://doi.org/10.2989/16073606.2013.779945, MR3043668.
10.2989/16073606.2013.779945
Web of Science® Google Scholar
4 Doha E. H., Abd-Elhameed W. M., and Youssri Y. H., Second kind Chebyshev operational matrix algorithm for solving differential equations of Lane-Emden type, New Astronomy. (2013) 23-24, 113–117, https://doi.org/10.1016/j.newast.2013.03.002.
10.1016/j.newast.2013.03.002
Web of Science® Google Scholar
5 Abd-Elhameed W. M., Doha E. H., and Youssri Y. H., New wavelets collocation method for solving second-order multipoint boundary value problems using Chebyshev polynomials of third and fourth kinds, Abstract and Applied Analysis. (2013) 2013, 9, https://doi.org/10.1155/2013/542839, 542839.
10.1155/2013/542839
Google Scholar
6 Constantmldes A., Applied Numerical Methods With Personal Computers, 1987, McGraw-Hill, New York, NY, USA.
Google Scholar
7 Newland D. E., An Introduction to Random Vibrations, Spectral and Wavelet Analysis, 1993, Longman Scientific and Technical, New York, NY, USA.
Google Scholar
8 Pašić M., Fite-Wintner-Leighton-type oscillation criteria for second-order differential equations with nonlinear damping, Abstract and Applied Analysis. (2013) 2013, 10, https://doi.org/10.1155/2013/852180, 852180, MR3034985, ZBL06161384.
10.1155/2013/852180
Google Scholar
9 Daoudi-Merzagui N., Derrab F., and Boucherif A., Subharmonic solutions of nonautonomous second order differential equations with singular nonlinearities, Abstract and Applied Analysis. (2012) 2012, 20, 903281, https://doi.org/10.1155/2012/903281, MR2903818, ZBL1244.34062.
10.1155/2012/903281
Google Scholar
10 Turkyilmazoglu M., Effective computation of exact and analytic approximate solutions to singular nonlinear equations of Lane-Emden-Fowler type, Applied Mathematical Modelling. (2013) 37, 7539–7548.
10.1016/j.apm.2013.02.014
Web of Science® Google Scholar
11 Doha E. H. and Abd-Elhameed W. M., Efficient solutions of multidimensional sixth-order boundary value problems using symmetric generalized Jacobi-Galerkin method, Abstract and Applied Analysis. (2012) 2012, 19, https://doi.org/10.1155/2012/749370, 749370, MR2926876, ZBL1246.65121.
10.1155/2012/749370
Google Scholar
12 Bratu G., Sur les équations intégrales non linéaires, Bulletin de la Société Mathématique de France. (1914) 42, 113–142, MR1504727.
10.24033/bsmf.943
Google Scholar
13 Gel′fand I. M., Some problems in the theory of quasilinear equations, American Mathematical Society Translations. (1963) 29, 295–381, MR0153960.
10.1090/trans2/029/12
Google Scholar
14 Serghini Mounim A. and de Dormale B. M., From the fitting techniques to accurate schemes for the Liouville-Bratu-Gelfand problem, Numerical Methods for Partial Differential Equations. (2006) 22, no. 4, 761–775, https://doi.org/10.1002/num.20116, MR2230270, ZBL1099.65098.
10.1002/num.20116
Web of Science® Google Scholar
15 Syam M. I. and Hamdan A., An efficient method for solving Bratu equations, Applied Mathematics and Computation. (2006) 176, no. 2, 704–713, https://doi.org/10.1016/j.amc.2005.10.021, MR2232062, ZBL1093.65108.
10.1016/j.amc.2005.10.021
Web of Science® Google Scholar
16 Wazwaz A.-M., Adomian decomposition method for a reliable treatment of the Bratu-type equations, Applied Mathematics and Computation. (2005) 166, no. 3, 652–663, https://doi.org/10.1016/j.amc.2004.06.059, MR2151056, ZBL1073.65068.
10.1016/j.amc.2004.06.059
Web of Science® Google Scholar
17 Abbasbandy S., Hashemi M. S., and Liu C.-S., The Lie-group shooting method for solving the Bratu equation, Communications in Nonlinear Science and Numerical Simulation. (2011) 16, no. 11, 4238–4249, https://doi.org/10.1016/j.cnsns.2011.03.033, MR2806735, ZBL1222.65067.
10.1016/j.cnsns.2011.03.033
Web of Science® Google Scholar
18 Caglar H., Caglar N., Özer M., Valarıstos A., and Anagnostopoulos A. N., B-spline method for solving Bratu′s problem, International Journal of Computer Mathematics. (2010) 87, no. 8, 1885–1891, https://doi.org/10.1080/00207160802545882, MR2665758, ZBL1197.65090.
10.1080/00207160802545882
Web of Science® Google Scholar
19 Khuri S. A., A new approach to Bratu′s problem, Applied Mathematics and Computation. (2004) 147, no. 1, 131–136, https://doi.org/10.1016/S0096-3003(02)00656-2, MR2007684, ZBL1032.65084.
10.1016/S0096-3003(02)00656-2
Web of Science® Google Scholar
20 Deeba E., Khuri S. A., and Xie S., An algorithm for solving boundary value problems, Journal of Computational Physics. (2000) 159, no. 2, 125–138, https://doi.org/10.1006/jcph.2000.6452, MR1752614, ZBL0959.65091.
10.1006/jcph.2000.6452
Web of Science® Google Scholar
21 Boyd J. P., One-point pseudospectral collocation for the one-dimensional Bratu equation, Applied Mathematics and Computation. (2011) 217, no. 12, 5553–5565, https://doi.org/10.1016/j.amc.2010.12.029, MR2770174, ZBL1222.65070.
10.1016/j.amc.2010.12.029
Web of Science® Google Scholar
22 Jafari H., Yousefi S. A., Firoozjaee M. A., Momani S., and Khalique C. M., Application of Legendre wavelets for solving fractional differential equations, Computers & Mathematics with Applications. (2011) 62, no. 3, 1038–1045, https://doi.org/10.1016/j.camwa.2011.04.024, MR2824691, ZBL1228.65253.
10.1016/j.camwa.2011.04.024
Web of Science® Google Scholar
23 Mohammadi F. and Hosseini M. M., A new Legendre wavelet operational matrix of derivative and its applications in solving the singular ordinary differential equations, Journal of the Franklin Institute. (2011) 348, no. 8, 1787–1796, https://doi.org/10.1016/j.jfranklin.2011.04.017, MR2841880, ZBL1237.65079.
10.1016/j.jfranklin.2011.04.017
Web of Science® Google Scholar
24 Razzaghi M. and Yousefi S., The Legendre wavelets operational matrix of integration, International Journal of Systems Science. (2001) 32, no. 4, 495–502, https://doi.org/10.1080/002077201300080910, MR1960533, ZBL1006.65151.
10.1080/00207720120227
Web of Science® Google Scholar
25 Razzaghi M. and Yousefi S., Legendre wavelets method for the solution of nonlinear problems in the calculus of variations, Mathematical and Computer Modelling. (2001) 34, no. 1-2, 45–54, https://doi.org/10.1016/S0895-7177(01)00048-6, MR1834564.
10.1016/S0895-7177(01)00048-6
Web of Science® Google Scholar
26 Razzaghi M. and Yousefi S., Legendre wavelets method for constrained optimal control problems, Mathematical Methods in the Applied Sciences. (2002) 25, no. 7, 529–539, https://doi.org/10.1002/mma.299.abs, MR1895116, ZBL1001.49033.
10.1002/mma.299
Web of Science® Google Scholar
27 Babolian E. and Fattahzadeh F., Numerical solution of differential equations by using Chebyshev wavelet operational matrix of integration, Applied Mathematics and Computation. (2007) 188, no. 1, 417–426, https://doi.org/10.1016/j.amc.2006.10.008, MR2327367, ZBL1117.65178.
10.1016/j.amc.2006.10.008
Web of Science® Google Scholar
28 Dehghan M. and Saadatmandi A., Chebyshev finite difference method for Fredholm integro-differential equation, International Journal of Computer Mathematics. (2008) 85, no. 1, 123–130, https://doi.org/10.1080/00207160701405436, MR2376026, ZBL1131.65107.
10.1080/00207160701405436
Web of Science® Google Scholar
29 Saadatmandi A. and Dehghan M., A new operational matrix for solving fractional-order differential equations, Computers & Mathematics with Applications. (2010) 59, no. 3, 1326–1336, https://doi.org/10.1016/j.camwa.2009.07.006, MR2579495, ZBL1189.65151.
10.1016/j.camwa.2009.07.006
Web of Science® Google Scholar
30 Zhu L. and Fan Q., Solving fractional nonlinear Fredholm integro-differential equations by the second kind Chebyshev wavelet, Communications in Nonlinear Science and Numerical Simulation. (2012) 17, no. 6, 2333–2341, https://doi.org/10.1016/j.cnsns.2011.10.014, MR2877679, ZBL06056883.
10.1016/j.cnsns.2011.10.014
Web of Science® Google Scholar
31 Li Y., Solving a nonlinear fractional differential equation using Chebyshev wavelets, Communications in Nonlinear Science and Numerical Simulation. (2010) 15, no. 9, 2284–2292, https://doi.org/10.1016/j.cnsns.2009.09.020, MR2602712, ZBL1222.65087.
10.1016/j.cnsns.2009.09.020
Web of Science® Google Scholar
32 Saeedi H., Mohseni Moghadam M., Mollahasani N., and Chuev G. N., A CAS wavelet method for solving nonlinear Fredholm integro-differential equations of fractional order, Communications in Nonlinear Science and Numerical Simulation. (2011) 16, no. 3, 1154–1163, https://doi.org/10.1016/j.cnsns.2010.05.036, MR2736623, ZBL1221.65354.
10.1016/j.cnsns.2010.05.036
Web of Science® Google Scholar
33 Saeedi H. and Moghadam M. M., Numerical solution of nonlinear Volterra integro-differential equations of arbitrary order by CAS wavelets, Communications in Nonlinear Science and Numerical Simulation. (2011) 16, no. 3, 1216–1226, https://doi.org/10.1016/j.cnsns.2010.07.017, MR2736629, ZBL1221.65140.
10.1016/j.cnsns.2010.07.017
Web of Science® Google Scholar
34 Cheng C. F., Tsay Y. T., and Wu T. T., Walsh operational matrices for fractional calculus and their application to distributed systems, Journal of the Franklin Institute. (1977) 303, no. 3, 267–284, 2-s2.0-0001549690.
10.1016/0016-0032(77)90029-1
Web of Science® Google Scholar
35 Chang R. Y. and Wang M. L., Shifted Legendre direct method for variational problems, Journal of Optimization Theory and Applications. (1983) 39, no. 2, 299–307, https://doi.org/10.1007/BF00934535, MR693689, ZBL0481.49004.
10.1007/BF00934535
Web of Science® Google Scholar
36 Horng I. R. and Chou J. H., Shifted Chebyshev direct method for solving variational problems, International Journal of Systems Science. (1985) 16, no. 7, 855–861, https://doi.org/10.1080/00207728508926718, MR804297, ZBL0568.49019.
10.1080/00207728508926718
Web of Science® Google Scholar
37 Gu J. S. and Jiang W. S., The Haar wavelets operational matrix of integration, International Journal of Systems Science. (1996) 27, no. 7, 623–628, https://doi.org/10.1080/00207729608929258.
10.1080/00207729608929258
Web of Science® Google Scholar
38 Khellat F. and Yousefi S. A., The linear Legendre mother wavelets operational matrix of integration and its application, Journal of the Franklin Institute. (2006) 343, no. 2, 181–190, https://doi.org/10.1016/j.jfranklin.2005.11.002, MR2204243, ZBL1127.65105.
10.1016/j.jfranklin.2005.11.002
Web of Science® Google Scholar
39 Mason J. C. and Handscomb D. C., Chebyshev Polynomials, 2003, Chapman & Hall/CRC, Boca Raton, Fla, USA, MR1937591.
Google Scholar
40 Canuto C., Hussaini M. Y., Quarteroni A., and Zang T. A., Spectral Methods in Fluid Dynamics, 1988, Springer, New York, NY, USA, Springer Series in Computational Physics, MR917480.
10.1007/978-3-642-84108-8
Google Scholar
41 Eslahchi M. R., Dehghan M., and Ahmadi S., The general Jacobi matrix method for solving some nonlinear ordinary differential equations, Applied Mathematical Modelling. (2012) 36, no. 8, 3387–3398, https://doi.org/10.1016/j.apm.2011.09.082, MR2920899, ZBL1252.65121.
10.1016/j.apm.2011.09.082
Web of Science® Google Scholar

Citing Literature

All articles

New Spectral Second Kind Chebyshev Wavelets Algorithm for Solving Linear and Nonlinear Second-Order Differential Equations Involving Singular and Bratu Type Equations

Abstract

1. Introduction

2. Some Properties of Second Kind Chebyshev Polynomials and Their Shifted Forms

2.1. Second Kind Chebyshev Polynomials

2.2. Shifted Second Kind Chebyshev Polynomials

3. Shifted Second Kind Chebyshev Operational Matrix of Derivatives

3.1. Function Approximation

3.2. Convergence Analysis

4. Second-Order Two-Point Boundary Value Problems

4.1. Linear Second-Order Two-Point Boundary Value Problems

4.2. Nonlinear Second-Order Two-Point Boundary Value Problems

5. Numerical Results and Discussions

6. Concluding Remarks

Acknowledgments

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

New Spectral Second Kind Chebyshev Wavelets Algorithm for Solving Linear and Nonlinear Second-Order Differential Equations Involving Singular and Bratu Type Equations

Abstract

1. Introduction

2. Some Properties of Second Kind Chebyshev Polynomials and Their Shifted Forms

2.1. Second Kind Chebyshev Polynomials

2.2. Shifted Second Kind Chebyshev Polynomials

3. Shifted Second Kind Chebyshev Operational Matrix of Derivatives

3.1. Function Approximation

3.2. Convergence Analysis

4. Second-Order Two-Point Boundary Value Problems

4.1. Linear Second-Order Two-Point Boundary Value Problems

4.2. Nonlinear Second-Order Two-Point Boundary Value Problems

5. Numerical Results and Discussions

6. Concluding Remarks

Acknowledgments

References

Citing Literature

Figures

References

Related

Information