The Itô Integral with respect to an Infinite Dimensional Lévy Process: A Series Approach

Definition 1. Let p ≥ 1 be arbitrary.

• (1)

  We define the Lebesgue space

  $$ (5)
  where 𝔻([0, T]; E) denotes the Skorokhod space consisting of all càdlàg functions from [0, T] to E, equipped with the supremum norm.

• (2)

  We denote by $$ the space of all E-valued adapted processes $$.

• (3)

  We denote by $$ the space of all E-valued martingales $$.

• (4)

  We define the factor spaces

  $$ (6)
  $$ (7)
  where $$ denotes the subspace consisting of all $$ with M = 0 up to indistinguishability.

Remark 2. Let us emphasize the following.

• (1)

  Since the Skorokhod space 𝔻([0, T]; E) equipped with the supremum norm is a Banach space, the Lebesgue space $$ equipped with the standard norm

  $$ (8)
  is a Banach space too.

• (2)

  By the completeness of the filtration (ℱ_t) _t≥0, adaptedness of an element $$ does not depend on the choice of the representative. This ensures that the factor space $$ of adapted processes is well defined.

• (3)

  The definition of E-valued martingales relies on the existence of conditional expectation in Banach spaces, which has been established in [1, Proposition 1.10].

Lemma 3. Let p ≥ 1 be arbitrary. Then, the following statements are true:

• (1)

  $$ is closed in $$;

• (2)

  $$ is closed in $$.

Proof. Let $$ be a sequence, and let $$ be such that Mⁿ → M in $$. Furthermore, let τ ≤ T be a bounded stopping time. Then, we have

showing that M_τ ∈ L^p(Ω, ℱ_τ, ℙ; E). Furthermore, we have By Doob’s optional stopping theorem (which also holds true for E-valued martingales; see [2, Remark 2.2.5]), it follows that Using Doob’s optional stopping theorem again, we conclude that $$, proving the first statement.

Now, let $$ be a sequence, and let $$ be such that Xⁿ → X in $$. Then, for each t ∈ [0, T], we have

and, hence, ℙ-almost surely $$ for some subsequence (n_k) _k∈ℕ, showing that X_t is ℱ_t-measurable. This proves that $$, providing the second statement.

Lemma 4. Let H be a separable Hilbert space, and let (h_n) _n∈ℕ ⊂ H be a sequence with 〈h_n, h_m〉 _H = 0 for n ≠ m. Then, the following statements are equivalent.

• (1)

  The series $$ converges in H.

• (2)

  The series ∑_n∈ℕ h_n converges unconditionally in H.

• (3)

  One has $$.

If the previous conditions are satisfied, then one has

Proof. This follows from [22, Theorem  12.6] and [23, Satz  V.4.8].

Proposition 5. Let X be an H-valued, predictable process with

Then, for every orthonormal basis (f_k) _k∈ℕ of H, the series converges unconditionally in $$, and its value does not depend on the choice of the orthonormal basis (f_k) _k∈ℕ.

Proof. Let (f_k) _k∈ℕ be an orthonormal basis of H. For j, k ∈ ℕ with j ≠ k, we have

Moreover, by the Itô isometry for the real-valued Itô integral and the monotone convergence theorem, we obtain Therefore, by (17) and Lemma 4, the series (18) converges unconditionally in $$.

Now, let (g_k) _k∈ℕ be another orthonormal basis of H. We define $$ by

Let h ∈ H be arbitrary. Then, we have and the identity For all x ∈ H, we have and, by the Cauchy-Schwarz inequality, Therefore, by the Itô isometry for the real-valued Itô integral and Lebesgue′s dominated convergence theorem together with (17), we obtain Analogously, we prove that Therefore, denoting by $$ representatives of 𝕁^f, 𝕁^g, we obtain By separability of H, we deduce that Consequently, we have Implying that 𝕁^f = 𝕁^g. This proves that the value of the series (18) does not depend on the choice of the orthonormal basis.

Definition 6. For every H-valued, predictable process X satisfying (17), we define the Itô integral $$ as

where (f_k) _k∈ℕ denotes an orthonormal basis of H.

Remark 7. As the proof of Proposition 5 shows, the components of the Itô integral X · M are pairwise orthogonal elements of the Hilbert space $$.

Proposition 8. For every H-valued, predictable process X satisfying (17), one has the Itô isometry

Proof. Let (f_k) _k∈ℕ be an orthonormal basis of H. According to (19), we have

Thus, by Lemma 4 and (20), we obtain finishing the proof.

Proposition 9. Let X be a H-valued simple process of the form

with 0 = t₁ < ⋯<t_n+1 = T and $$-measurable random variables X_i : Ω → H for i = 0, …, n. Then, one has

Proof. Let (f_k) _k∈ℕ be an orthonormal basis of H. Then, for each k ∈ ℕ, the process 〈X, f_k〉 is a real-valued simple process with representation

Thus, by the definition of the real-valued Itô integral for simple processes, we obtain finishing the proof.

Lemma 10. Let X be a H-valued, predictable process satisfying (17). Then, for every orthonormal basis (f_k) _k∈ℕ of H, one has

where the convergence takes place in $$.

Proof. We define the integral process

and the sequence (𝕀ⁿ) _n∈ℕ of partial sums by By (17) we have $$ and $$. Furthermore, by Lebesgue′s dominated convergence theorem, we have which concludes the proof.

Remark 11. As a consequence of the Doob-Meyer decomposition theorem, for two square-integrable martingales $$, there exists (up to indistinguishability) a unique real-valued, predictable process 〈X, Y〉 with finite variation paths and 〈X, Y〉 ₀ = 0 such that 〈X, Y〉 _H − 〈X, Y〉 is a martingale.

Proposition 12. For every H-valued, predictable process X satisfying (17), one has

Proof. Let (f_k) _k∈ℕ be an orthonormal basis of H. We define the process 𝕁 : = X · M and the sequence (𝕁ⁿ) _n∈ℕ of partial sums by

By Proposition 5, we have Defining the integral process 𝕀 by (40) and the sequence (𝕀ⁿ) _n∈ℕ of partial sums by (41), using Lemma 10, we have Furthermore, we define the process $$ and the sequence $$ as Then, we have $$. Indeed, for each n ∈ ℕ, we have For every k ∈ ℕ, the quadratic variation of the real-valued process 〈X, f_k〉 _H · M is given by see, for example, [12, Theorem  I.4.40.d], which shows that Mⁿ is a martingale. Since $$, we deduce that $$.

Next, we prove that Mⁿ → M in $$. Indeed, since

by the Cauchy-Schwarz inequality and (45) we obtain Therefore, together with (46), we get showing that Mⁿ → M in $$. Now, Lemma 3 yields that $$, which concludes the proof.

Theorem 13. Let $$ be another square-integrable martingale, and let X, Y be two H-valued, predictable processes satisfying (17) and

Then, one has

Proof . Using Proposition 12 and the identities

identity (54) follows from a straightforward calculation.

Proposition 14. Let $$ be another square-integrable martingale such that 〈M, N〉 = 0, and let X, Y be two H-valued, predictable processes satisfying (17) and (53). Then, one has

Proof. Using Remark 11, Theorem 13, and the hypothesis 〈M, N〉 = 0, we obtain

completing the proof.

Definition 15. A sequence (M^j) _j∈ℕ of real-valued Lévy processes is called a sequence of standard Lévy processes if it consists of square-integrable martingales with 〈M^j, M^k〉 _t = δ_jk · t for all j, k ∈ ℕ. Here, δ_jk denotes the Kronecker delta

For the rest of this section, let (M^j) _j∈ℕ be a sequence of standard Lévy processes.

Proposition 16. For every ℓ²(H)-valued, predictable process X with

the series converges unconditionally in $$.

Proof. For j, k ∈ ℕ with j ≠ k, we have 〈M^j, M^k〉 = 0, and, hence, by Proposition 14, we obtain

Moreover, by the Itô isometry (Proposition 8) and the monotone convergence theorem, we have Thus, by (61) and Lemma 4, the series (62) converges unconditionally in $$.

Remark 17. As the proof of Proposition 16 shows, the components of the Itô integral ∑_j∈ℕ X^j · M^j are pairwise orthogonal elements of the Hilbert space $$.

Proposition 18. For each ℓ²(H)-valued, predictable process X satisfying (61), one has the Itô isometry

Proof . Using (63), Lemma 4, and identity (64), we obtain

completing the proof.

Proposition 19. Let X be a ℓ²(H)-valued simple process of the form

with 0 = t₁ < ⋯<t_n+1 = T and $$-measurable random variables X_i : Ω → ℓ²(H) for i = 0, …, n. Then, one has

Proof . For each j ∈ ℕ, the process X^j is a H-valued simple process having the representation

Hence, by Proposition 9, we obtain which finishes the proof.

Definition 20. A U-valued càdlàg, adapted process L is called a Lévy process if the following conditions are satisfied.

• (1)

  We have L₀ = 0.

• (2)

  L_t − L_s is independent of ℱ_s for all s ≤ t.

• (3)

  We have $$ for all s ≤ t.

Definition 21. A U-valued Lévy process L with $$ and 𝔼[L_t] = 0 for all t ≥ 0 is called a square-integrable Lévy martingale.

Lemma 22. Let L be a U-valued square-integrable Lévy martingale with covariance operator Q, let V be another separable Hilbert space, and let Φ : U → V be an isometric isomorphism. Then, the process Φ(L) is a V-valued square-integrable Lévy martingale with covariance operator Q_Φ : = ΦQΦ⁻¹.

Proof . The process Φ(L) is a V-valued càdlàg, adapted process with Φ(L₀) = Φ(0) = 0. Let s ≤ t be arbitrary. Then, the random variable Φ(L_t) − Φ(L_s) = Φ(L_t − L_s) is independent of ℱ_s, and we have

Moreover, for each t ∈ ℝ₊, we have showing that Φ(L) is a V-valued square-integrable Lévy martingale.

Let t, s ∈ ℝ₊ and v_i ∈ V, i = 1,2 be arbitrary, and set u_i : = Φ⁻¹v_i ∈ U,  i = 1,2. Then, we have

showing that the Lévy martingale Φ(L) has the covariance operator Q_Φ.

Proposition 23. Let L be a U-valued square-integrable Lévy martingale with covariance operator Q. Then, the sequence (M^j) _j∈ℕ given by

is a sequence of standard Lévy processes.

Proof. For each j ∈ ℕ, the process M^j is a real-valued square-integrable Lévy martingale. By (73), for all j, k ∈ ℕ, we obtain

showing that (M^j) _j∈ℕ is a sequence of standard Lévy processes.

Definition 24. For every ℓ²(H)-valued, predictable process X satisfying (61), we define the Itô integral $$ as

Remark 25. Note that $$, where $$ denotes the space of Hilbert-Schmidt operators from ℓ² to H. In [21], the Itô integral for $$-valued processes with respect to an $$-valued Wiener process has been constructed in the usual fashion (first for elementary and afterwards for general processes), and then the series representation (88) has been proven; see [21, Proposition  2.2.1].

Now, let (μ_k) _k∈ℕ be another sequence with $$, and let $$ be an isometric isomorphism such that

By Lemma 22, the process Φ(L) is a $$-valued, square integrable Lévy martingale with covariance operator Q_Φ, and by Proposition 23, the sequence (N^k) _k∈ℕ given by

Theorem 26. Let Ψ ∈ L(ℓ²(H)) be an isometric isomorphism such that

Then, for every ℓ²(H)-valued, predictable process X satisfying (61), one has and the identity

Proof. Since Ψ is an isometry, by (61), we have

showing (92). Moreover, by (89), we have and, hence, we get By (86) and (96), the vectors $$ and $$ are eigenvectors of Q with corresponding eigenvalues (λ_j) _j∈ℕ and (μ_k) _k∈ℕ. Therefore, and since Φ is an isometry, for j, k ∈ ℕ with λ_j ≠ μ_k, we obtain Let h ∈ H be arbitrary. Then, we have Since (λ_j) _j∈ℕ and (μ_k) _k∈ℕ are eigenvalues of Q, for each j ∈ ℕ, there are only finitely many k ∈ ℕ such that λ_j = μ_k. Therefore, by (97), and since $$ is an orthonormal basis of $$, we obtain Thus, taking into account (91) gives us Since h ∈ H was arbitrary, using the separability of H as in the proof of Proposition 5, we arrive at (93).

Remark 27. From a geometric point of view, Theorem 26 says that the “angle” measured by the Itô integral is preserved under isometries.

Lemma 28. The following statements are true.

• (1)

  The process Φ_λ(L) is an $$-valued square-integrable Lévy martingale with covariance operator $$.

• (2)

  One has

  $$ (107)

Proof. By Lemma 22, the process Φ_λ(L) is an $$-valued square-integrable Lévy martingale with covariance operator $$. Furthermore, by (105) and (101), for all j ∈ ℕ, we obtain

showing (107).

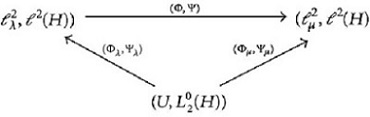
Lemma 29. For all h ∈ H and w ∈ ℓ²(H), one has

Proof. By (101) and (111), the vectors $$ and $$ are eigenvectors of Q with corresponding eigenvalues (λ_j) _j∈ℕ and (μ_k) _k∈ℕ. Therefore, for j, k ∈ ℕ with λ_j ≠ μ_k, we have $$. For each $$, we obtain

Let w ∈ ℓ²(H) be arbitrary. By (106), we have and, hence, Therefore, for all h ∈ H and w ∈ ℓ²(H), we obtain finishing the proof.

Proposition 30. The following statements are true.

• (1)

  Φ_λ(L) is an $$-valued Lévy process with covariance operator $$, and one has

  $$ (122)

• (2)

  Φ_μ(L) is an $$-valued Lévy process with covariance operator $$, and one has

  $$ (123)

• (3)

  For every $$-valued, predictable process X with (109), one has

  $$ (124)
  and the identity (116).

Proof. The first two statements follow from Lemma 28. Since Ψ_λ and Ψ_μ are isometries, we obtain

which, together with (109), yields (124). Now, Theorem 26 applies by virtue of Lemma 29 and yields proving (116).

Definition 31. For every $$-valued process X satisfying (109), we define the Itô-Integral $$ by (110).

Proposition 32. For every $$-valued, predictable process X satisfying (109), the process (ξ^j) _j∈ℕ given by

is a ℓ²(H)-valued, predictable process, and, one has where the right-hand side of (129) converges unconditionally in $$.

Proof. Since Φ_λ is an isometry, for each j ∈ ℕ, we obtain

Thus, by Definitions 31 and 24, we obtain and, by Proposition 16, the series converges unconditionally in $$.

Remark 33. By Remark 17 and the proof of Proposition 32, the components of the Itô integral ∑_j∈ℕ ξ^j · M^j are pairwise orthogonal elements of the Hilbert space $$.

Proposition 34. For every $$-valued process X satisfying (109), one has the Itô isometry

Proof. By the Itô isometry (Proposition 18), and since Ψ_λ is an isometry, we obtain

completing the proof.

Proposition 35. Let X be a L(U, H)-valued simple process of the form

with 0 = t₁ < ⋯<t_n+1 = T and $$-measurable random variables X_i : Ω → L(U, H) for i = 0, …, n. Then, one has

Proof. The process $$ is an ℓ²(H)-valued simple process having the representation

Thus, by Proposition 19, and since Φ_λ is an isometry, we obtain completing the proof.