Falkner-Skan Flow of a Maxwell Fluid with Heat Transfer and Magnetic Field
Abstract
This investigation deals with the Falkner-Skan flow of a Maxwell fluid in the presence of nonuniform applied magnetic fi eld with heat transfer. Governing problems of flow and heat transfer are solved analytically by employing the homotopy analysis method (HAM). Effects of the involved parameters, namely, the Deborah number, Hartman number, and the Prandtl number, are examined carefully. A comparative study is made with the known numerical solution in a limiting sense and an excellent agreement is noted.
1. Introduction
The Falkner-Skan problem under various aspects has attracted the attention of several researchers [1]. This problem under various aspects has been discussed extensively for viscous fluid. The interested readers may consult the studies in [2–11] for detailed information in viscous fluids. There are several materials which do not obey the Newton′s law of viscosity, for example, biological products like blood and vaccines, foodstuffs like honey, ketchup, butter, and mayonnaise, certain paints, cosmetic products, pharmaceutical chemicals and so forth. These fluids are characterized as the non-Newtonian fluids. Investigation of such fluids is very useful in industrial, engineering, and biological applications. However, such fluids cannot be studied by employing a single constitutive relationship. This is due to diverse properties of non-Newtonian fluids in nature. These non-Newtonian fluid models are discussed in view of three main categories, namely, the differential, the rate, and the integral types. The simplest subclass of rate type fluids is called Maxwell. The Maxwell fluid allows for the relaxation effects which cannot be predicted in differential type fluids, namely, second, third, and fourth grades. Recently, there has been an increasing interest in the theory of rate type fluids and, in particular, a Maxwell fluid model has been accorded much attention. The Falkner-Skan wedge flow of a non-Newtonian fluid was firstly investigated by Rajagopal et al. [12]. Massoudi and Ramezan [13] discussed the effect of injection or suction on the Falkner-Skan flows of second grade fluids. The Falkner-Skan wedge flow of power-law fluids embedded in a porous medium is investigated by Kim [14]. Olagunju [15] studied this flow problem for viscoelastic fluid. In [10–15], the attention has been given to the differential type fluids. To the best of our knowledge, no one investigated the Falkner-Skan flow problem for rate type fluids.
In [10], Yao has examined the Falkner-Skan wedge flow. He established series solution for the velocity and temperature by using homotopy analysis method [16–25]. The purpose of the present contribution is to extend the flow analysis of study [10] in two directions. The first generalization is concerned with the consideration of electrically conducting fluid. Such analysis has inserted in power generators the cooling of reactors, MHD accelerators, the design of heat exchanges and electrostatic filters. Secondly, we consider the Maxwell fluid instead of viscous fluid. The rest of the paper is arranged as follows. The description of the problem is presented in Section 2. Section 3 develops the homotopy solutions for velocity and temperature. Convergence of the derived solution is examined in Section 4. Further, the variations of embedded parameters have been discussed in this section.
2. Problem Development
3. Homotopy Analysis Solutions
4. Convergence of the Homotopy Solutions
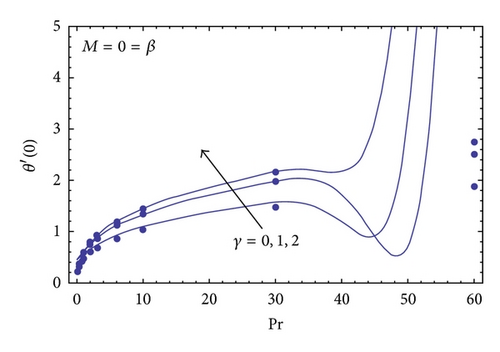
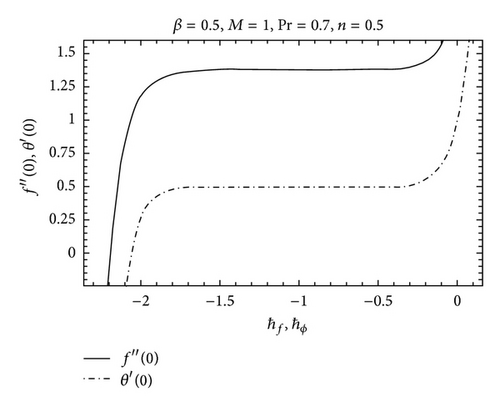
Obviously the auxiliary parameters ℏf and ℏθ in the series solutions (31) and (32) have a definite role in adjusting and controlling the convergence. For the admissible values of ℏf and ℏθ, the ℏf and ℏθ curves are portrayed for 15th-order of approximations. It is noticed that the ranges for the admissible values of ℏf and ℏθ are −1.5 ≤ ℏf ≤ −0.2 and −1.2 ≤ ℏθ ≤ −0.6 (Figure 1). Moreover, the series given by (31) and (32) converge in the whole region of η when ℏf = −0.5 and ℏθ = −0.8.
5. Results and Discussion
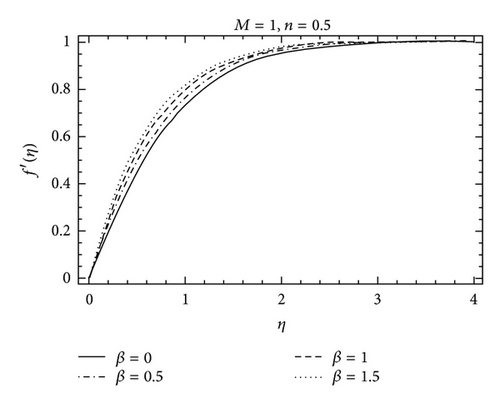
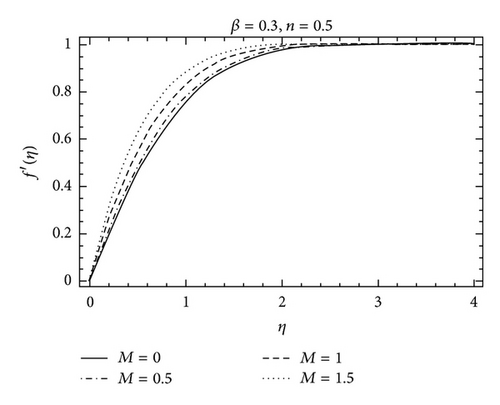
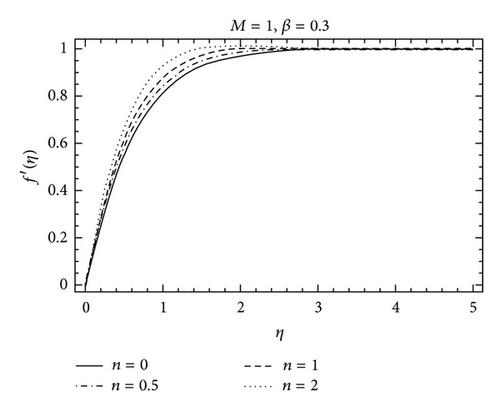
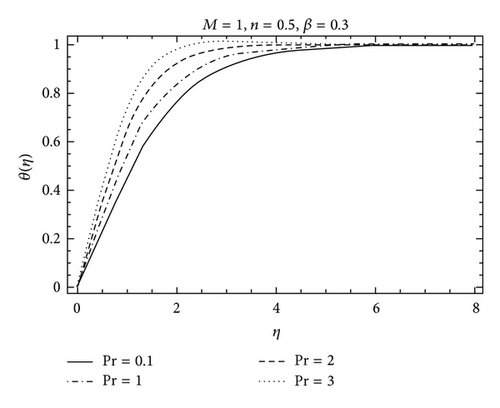
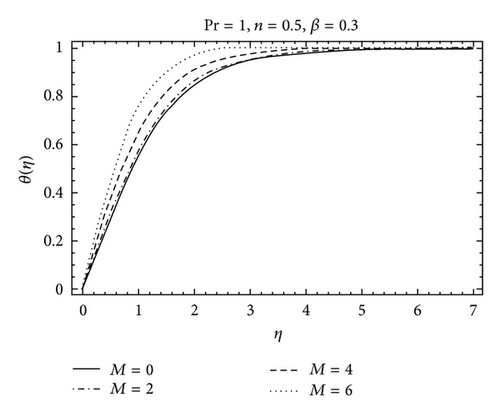
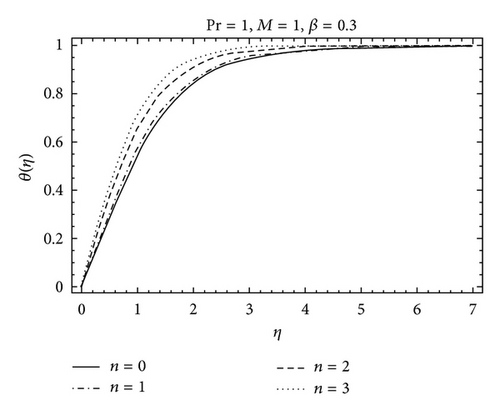
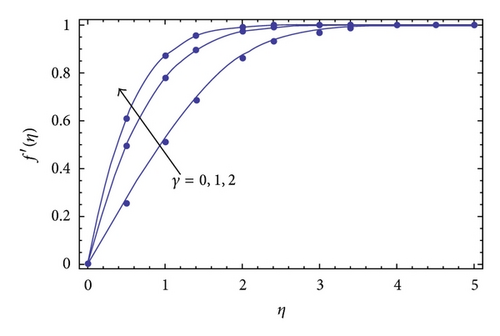
The purpose of this section is to investigate the variations of parameters including Deborah number γ, the constant n, Hartman number M, and the Prandtl number Pr on the velocity f′ and the temperature θ. The variation of the Deborah number β, Hartman number M, and the parameter n on the velocity f′ can be seen in Figures 2–5. It is found from Figure 2 that the boundary layer thickness decreases with an increase in γ. Figure 3 is plotted for the effects of Hartman number M on the velocity profile f′. The effects of M on f′ are qualitatively similar to those of γ. Figure 4 depicts the velocity field for different values of parameter n. Clearly f′ is an increasing function of n while the boundary layer thickness decreases. Figure 5 shows the effects of Prandtl number Pr on the temperature profile θ. The thermal boundary layer thickness decreases when Pr increases. The variation of Hartman number M on the temperature profile is shown in Figure 6. It is noticed that the temperature profile increases when M is increased. The effects of parameter n are shown in Figure 7. It is observed that an increase in the value of n decreases the thermal boundary layer thickness. Figures 8 and 9 are displayed to analyze the comparison of the present analytical results with the existing numerical solutions. An excellent agreement is found between the two solutions for different values of γ. In Table 1, we have computed the numerical values of f(η), f′(η), and f′′(η) for the comparison of the present analytical results with the numerical solution [26]. Table 2 is also a comparison between homotopy solution and numerical solution [26] in a special case. An excellent agreement is found between the two solutions.
| η | f(η) | f′(η) | f′′(η) | |||
|---|---|---|---|---|---|---|
| HAM | [26] | HAM | [26] | HAM | [26] | |
| 0.0 | 0.000000 | 0.00000 | 0.000000 | 0.000000 | 0.469600 | 0.46960 |
| 0.5 | 0.058643 | 0.05864 | 0.234228 | 0.23423 | 0.465038 | 0.46503 |
| 1.0 | 0.232990 | 0.23299 | 0.460633 | 0.46063 | 0.434379 | 0.43438 |
| 2.0 | 0.886821 | 0.86680 | 0.816695 | 0.81669 | 0.255669 | 0.25567 |
| 3.0 | 1.795568 | 1.79557 | 0.969092 | 0.96905 | 0.067713 | 0.06771 |
| 4.0 | 2.783886 | 2.78388 | 0.997770 | 0.99777 | 0.006875 | 0.00687 |
| 5.0 | 3.783235 | 3.78323 | 0.999937 | 0.99994 | 0.000258 | 0.00026 |
| Pr | γ = 0.0 | γ = 1.0 | γ = 2.0 | |||
|---|---|---|---|---|---|---|
| HAM | [26] | HAM | [26] | HAM | [26] | |
| 0.001 | 0.024492 | 0.02449 | 0.024831 | 0.02483 | 0.024922 | 0.02492 |
| 0.003 | 0.041546 | 0.04154 | 0.042523 | 0.04252 | 0.042780 | 0.04278 |
| 0.100 | 0.198031 | 0.19803 | 0.219502 | 0.21950 | 0.226096 | 0.22600 |
| 0.300 | 0.303712 | 0.30371 | 0.351471 | 0.35147 | 0.366813 | 0.36681 |
| 1.000 | 0.469601 | 0.46960 | 0.570475 | 0.57047 | 0.605204 | 0.60520 |
| 2.000 | 0.597234 | 0.59723 | 0.743721 | 0.74372 | 0.795991 | 0.79599 |
| 3.000 | 0.685967 | 0.68596 | 0.865224 | 0.86522 | 0.930362 | 0.93036 |