We present the analytical and multishaped solitary wave solutions for extended reduced Ostrovsky equation (EX-ROE). The exact solitary (traveling) wave solutions are expressed by three types of functions which are hyperbolic function solution, trigonometric function solution, and rational solution. These results generalized the previous results. Multishape solitary wave solutions such as loop-shaped, cusp-shaped, and hump-shaped can be obtained as well when the special values of the parameters are taken. The (G^′/G)-expansion method presents a wide applicability for handling nonlinear partial differential equations.

1. Introduction

The well-known Ostrovsky equation [1]

()

where c₀ is the velocity of dispersiveness linear waves, α is the nonlinear coefficient, and β and γ are dispersion coefficients, is a model for weakly nonlinear surface and internal waves in a rotating ocean.

For long waves, for which high-frequency dispersion is negligible, β = 0, and (1) becomes the so-called reduced Ostrovsky equation (ROE) [2]

()

Parkes [3] has studied (2) and found its periodic and solitary traveling wave solutions.

In fact, by applying the following transformation [4]:

()

to (2), we obtain the ROE in the neat form

()

Just as it mentioned in [5] and the reference therein, when δ = −1, (4) is referred to the Ostrovsky-Hunter equation (OHE). When δ = 1, (4) is referred to the Vakhnenko equation (VE), which is in order to model the propagation of waves in a relaxing medium [6, 7]. Parkes [3] pointed out that (4) is invariant under the transformation

()

so that the solutions of the OHE and VE are related in a simple way.

The purpose of this paper is to study the extended reduced Ostrovsky equation (EX-ROE):

()

where 𝔇 is defined previous, p, q, and β are arbitrary nonzero constants. It is originally derived by Morrison and Parkes [8] which dubbed it as modified generalized Vakhnenko equation (mGVE) when p = 2q. They found that not only does it have loop soliton solutions, hump-like and cusp-like soliton solutions, but it also has N-soliton solutions.

In order to investigate mGVE’s N-soliton solution, Morrison and Parkes [8] considered a Hirota-Satsuma-type shallow water wave equation [9] of the form

()

where p ≠ 0, q ≠ 0, and β is arbitrary constant. By using the transformation

()

where x₀ is a constant, (7) yields (6). So (6) and (7) are equivalent to each other under the transformation (8). Specifically, in (7), when p = 2q and β = −1, it was discussed by Ablowitz et al. [10] and was shown to be integrable by inverse scatting method. When p = q and β = −1, it was discussed by Hirota and Satsuma [11] and was shown to be integrable using Hirota’s bilinear technique. In [12], the authors referred to (6) with p = q = 1 and β an arbitrary nonzero constant as the generalized Vakhnenko equation (GVE). In fact, when p = q and β = 0, (6) can be written as

()

Clearly, solutions of the ROE are also solutions of (9) with p = ±1. So for arbitrary p, q, and β, if we obtain the solutions of EX-ROE, then we can also obtain the solutions of VE, GVE, mGVE, ROE, and OHE by taking the special values of p, q, and β.

The EX-ROE has been studied by several researchers. For example, Liu et al. [13] used Jacobi elliptic function method to obtain exact double periodic wave solutions and solitary wave solutions. Parkes [4] constructed periodic and solitary wave solutions of EX-ROE and gave the categorization of the solutions. Xie and Cai [14] used the bifurcation method of dynamic systems and simulation method of differential equations to get exact compacton and generalized kink wave solutions of EX-ROE. Stepanyants [15] applied the qualitative theory of differential equations to give a full classification of its solutions.

Recently, there are many methods being proposed to study the traveling wave solutions of nonlinear partial differential equations which are derived from physics, for example, [16–27]. As well as these methods, there are still many other methods; we cannot list all of them. Here we will use modified (G^′/G)-expansion method to investigate EX-ROE. As a result, three types of traveling wave solutions are were obtained. When the special values of the parameters are taken, they are reduced to some previous results which obtained by an other method.

The rest of the paper is organized as follows. In Section 2, we present a methodology of the modified (G^′/G)-expansion method. In Section 3, we apply the method to the extended reduced Ostrovsky equation. In Section 4, some conclusions are given.

2. Description of the Modified (G^′/G)-Expansion Method

The (G^′/G)-expansion method is first proposed by Wang et al. [28]. The useful (G^′/G)-expansion method is then widely used by many authors [29–32]. Then it is modified in [33–35]. The main steps are as follows.

Suppose that a nonlinear equation is given by

()

where u = u(x, t) is an unknown function and P is a polynomial in u = u(x, t) and its partial derivatives, in which the highest-order derivatives and nonlinear terms are involved. In the following we give the main steps of the (G^′/G)-expansion method.

Step 1. The traveling wave variable u(x, t) = u(ξ), ξ = x − ct, where c is a constant, permits us to reduce (10) to an ODE for u = u(ξ) in the form

()

Step 2. Suppose that the solution of (10) can be expressed by a polynomial in (G^′/G) as follows:

()

where G = G(ξ) satisfies the second-order linear ordinary differential equation (LODE) in the form

()

where α_−m, …, α_m, λ, and μ are constants to be determined later. The unwritten part in (12) is also a polynomial in (G^′/G), but the degree of which is generally equal to or less than m − 1. The positive integer m can be determined by considering the homogeneous balance between the highest-order derivatives and nonlinear terms appearing in (11).

Step 3. Substituting (12) into (11) and using (13), collecting all terms with the same order of (G^′/G) together, and then equating each coefficient of the resulting polynomial to zero yields a set of algebraic equations for α_m, α_m−1, …, α_−m, c, λ, and μ.

Step 4. Since the general solutions of (13) have been well known for us, then substituting α_m, α_m−1, …, α_−m and c and the general solutions of (13) into (12) we have more traveling wave solutions of the nonlinear differential equation (10).

The main idea of (G^′/G)-expansion method is to use an integrable ODE to expand a solution to a nonlinear partial differential equation (PDE) as a polynomial or rational function of the solution of the ODE. However, such an idea was also presented in [36–38]. The method used in this paper can be also thought of as the application of transformed rational function method used in [37] in some sense. Maybe the similar results can be obtained by using these very closely related methods. We plan to further study the EX-ROE in near future by using the methods proposed in [36–38]. We hope we can find much more interesting properties and new phenomenon of this equation.

3. Exact Traveling Wave Solutions of the Extended Reduced Ostrovsky Equation

In this section, we will use the (G^′/G)-expansion method to the extended reduced Ostrovsky equation to get exact traveling wave solutions.

First, in order to get traveling wave solutions, we need some transformation. Recall that in Section 1 we have stated that EX-ROE is equivalent to a Hirota-Satsuma-type shallow water wave equation (7) under the transformation of (8). So here we introduce a new variable W defined by

()

Substituting (14) into (7) yields

()

Now giving the traveling wave transformation W(X, T) = W(ξ), ξ = X − cT, where c is wave speed. Substituting them into (15) and integrating once, we have

()

where c₁ is integral constant that is to be determined later.

Considering the homogeneous balance between W_3ξ and

, we have

()

We suppose that

()

where the G = G(ξ) satisfies the second-order LODE,

()

and α₋₁, α₀, α₁, λ, and μ are constants to be determined later.

By using (18) and (19), it is derived that

()

By substituting (20)–(22) into (16) and collecting all terms with the same power of (G^′/G) together, the left-hand sides of (16) are converted into the polynomials in (G^′/G). Equating the coefficients of the polynomials to zero yields a set of simultaneous algebraic equations for α₋₁, α₀, α₁, λ, c, c₁, and μ as follows (denote A for (G^′/G)):

()

Solving the algebraic equations above yields

()

Substituting system (24) and (25) into (18), we have the formula of the solutions of (15) as follows:

()

where G satisfies (19), ξ = X − qT/(β + λ² − 4μ), and α₀ is an arbitrary constant.

Since the general solutions G = G(ξ) (hence G^′ = dG/dξ) of ODE (19) have been known for us, substituting the solutions of (19) into (24) and (25), we have the general traveling wave solutions of (15) as follows.

Case 1. When λ² − 4μ > 0, then we have the following exact traveling wave solution of (15):

()

where ξ = X − qT/(β + λ² − 4μ) and α₀, A₁, A₂ are arbitrary constants.

Case 2. When λ² − 4μ < 0, then we have the following exact traveling wave solution of (15):

()

where ξ = X − qT/(β + λ² − 4μ) and α₀, A₁, A₂ are arbitrary constants.

Case 3. When λ² − 4μ = 0, then we have the following exact rational solution of (15):

()

where ξ = X − qT/(β + λ² − 4μ) and α₀, A₁, A₂ are arbitrary constants.

Now we will show how to get exact traveling wave solutions of (6). From (8) and (14), the solution of EX-ROE (6) is given in parametric form, with T as the parameter, by

()

where

()

So by using (8), (14), (34), (35), (28), and (29), we obtain a parameterized hyperbolic-function-type traveling wave solution of (6) as follows:

()

where ξ = t − qT/(β + λ² − 4μ) and x₀ is an arbitrary constant.

By using (8), (14), (34), (35), (30), and (31), we obtain a parameterized trigonometric-function-type traveling wave solution of (6) as follows:

()

where ξ = t − qT/(β + λ² − 4μ) and x₀ is an arbitrary constant.

By using (8), (14), (34), (35), (32), and (33), we obtain a parameterized rational-type traveling wave solution of (6) as follows:

()

where ξ = t − qT/(β + λ² − 4μ) and x₀ is an arbitrary constant. To our knowledge, these solutions are presented for the first time; they are new exact solutions of EX-ROE.

If we take A₁ = 0, μ = 0, A₂ ≠ 0 and λ > 0, then (36) yields the following solitary wave solution of (6):

()

Now we will give some discussion of the solitary wave solution (42). Let λ = 2k, x₀ = 0; the solution (42) is reduced to the solution of (3.26) in [13] after correcting some minor errors [4]. Now from (35), we introduce a new variable:

()

where v = 1/c = (λ² + β)/q. In [8], the authors considered EX-ROE with p = 2q, β ≠ 0 as mGVE and obtained 1-soliton solution. In fact, if we take p = 2q, λ = 2k, the solitary wave solution (42) with (43) is reduced to the soliton solution (4.4) and (4.5) in [8]. From the above we can see that the solitary wave solution (3.26) in [4] and the 1-soliton solution of mGVE are just a special case of the solution (42) in this paper.

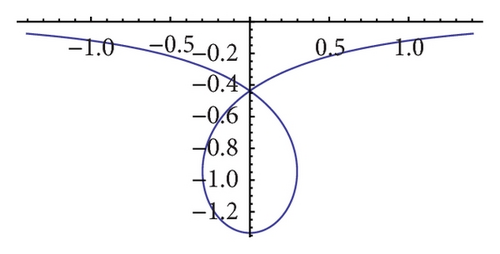
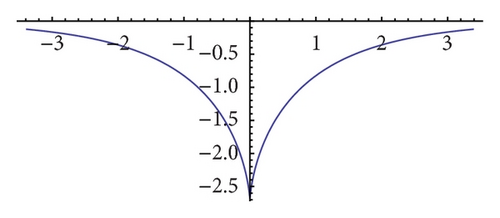
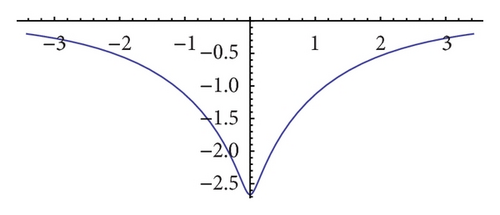
4. Multishaped Solitary Wave Solutions

In [8, 13], the authors showed that the solutions of (4.4) and (4.5), (3.26) and (3.28) may be of different types, namely, loops, cusps, or humps for different values of parameters β, k, p. Here we also show that by choosing different values of the parameters β, λ, p, q, different shape wave solutions can be obtained. As it is stated in Section 1, (9) reduces to VE when p = q = 1, β = 0. Taking solution (42) with (43), for example, let p = q = 1, β = 0, λ = 2k; then it is reduced to one-loop soliton solution (3.4) and (3.5) in [39]. On the other hand, because the solutions of OHE and VE are connected in a particularly simple way, if we take p = q = −1, β = 0, λ = 2k in (42), we can obtain one-loop soliton solution of OHE.

From above analysis, one can clearly see that the solutions obtained in this paper are generalized for the previous results because here we only take the special case A₁ = 0, μ = 0, A₂ ≠ 0, λ > 0 and give special discussion of solution (42). We conclude that if we take different values of the parameters A₁, A₂, λ, μ, p, q, abundancy of types of exact solutions can be obtained from solutions (36), (38), and (40). Here we omit the detailed discussion.

Instead, we give some discussion about solution (37). Science from this solution, multishaped solitary wave solutions can be obtained. Suppose A₁ ≠ 0, μ < 0, A₂ = 0, λ = 0; we reduce solution (37) to

()

We show that for different values of β, μ, and p, the solution (44) may be of different types. It also owns the property of being loop-shaped, cusp-shaped and hump-shaped, as shown in Figure 1.

Details are in the caption following the image — **Figure 1 (a)**
Open in figure viewer PowerPoint

The profile of solution (44) with p = 3, q = 1.5, t = 0, and x₀ = 0. For (a) loop-shaped β = 0.005, μ = −0.5, (b) cusp-shaped β = 0.05, μ = −1, and (c) hump-shaped β = 0.5, μ = −1.

5. Conclusion

In this paper, we use (G^′/G)-expansion method to study extended reduced Ostrovsky equation. Several pairs of generalized traveling wave solutions are given directly. These solutions extend the previous results to more general cases. At the same time, multishaped wave solutions can be obtained if the different parameters values are chosen. These explicit solitary wave solutions own the property of being loop-shaped, cusp-shaped, and hump-shaped. These exact traveling wave solutions are also helpful to further study this nonlinear equation which has their physical meaning. The method used in this paper has more advantages. It is direct and concise. Much tedious algebraic calculations can be finished by computer program such as MATHEMATICA and MAPLE. Many well-known nonlinear wave equations can be handled by this method.

Acknowledgment

The authors thank anonymous referees for valuable suggestions and comments which improve this paper readability and convincibility. This paper is supported by the Starting Research Founding of Wuhan Textile University.

References

1 Ostrovsky L. A., Nonlinear internal waves in a rotating ocean, Oceanology. (1978) 18, 119–125.
Google Scholar
2 Stepanyants Y. A., On stationary solutions of the reduced Ostrovsky equation: periodic waves, compactons and compound solitons, Chaos, Solitons & Fractals. (2006) 28, no. 1, 193–204, https://doi.org/10.1016/j.chaos.2005.05.020, MR2175554.
10.1016/j.chaos.2005.05.020
Web of Science® Google Scholar
3 Parkes E. J., Explicit solutions of the reduced Ostrovsky equation, Chaos, Solitons & Fractals. (2007) 31, no. 3, 602–610, https://doi.org/10.1016/j.chaos.2005.10.028, MR2262294, ZBL1138.35399.
10.1016/j.chaos.2005.10.028
Web of Science® Google Scholar
4 Parkes E. J., Periodic and solitary travelling-wave solutions of an extended reduced Ostrovsky equation, SIGMA. (2008) 4, article 053, 1–17, https://doi.org/10.3842/SIGMA.2008.053, MR2425639, ZBL1147.35101.
10.3842/SIGMA.2008.053
Google Scholar
5 Boyd J. P., Ostrovsky and Hunter′s generic wave equation for weakly dispersive waves: matched asymptotic and pseudospectral study of the paraboloidal travelling waves (corner and near-corner waves), European Journal of Applied Mathematics. (2005) 16, no. 1, 65–81, https://doi.org/10.1017/S0956792504005625, MR2148681.
10.1017/S0956792504005625
CAS Web of Science® Google Scholar
6 Vakhnenko V. A., Solitons in a nonlinear model medium, Journal of Physics A. (1992) 25, no. 15, 4181–4187, MR1177553, https://doi.org/10.1088/0305-4470/25/15/025, ZBL0754.35132.
10.1088/0305-4470/25/15/025
Web of Science® Google Scholar
7 Vakhnenko V. O., High-frequency soliton-like waves in a relaxing medium, Journal of Mathematical Physics. (1999) 40, no. 4, 2011–2020, https://doi.org/10.1063/1.532847, MR1683122, ZBL0946.35094.
10.1063/1.532847
Web of Science® Google Scholar
8 Morrison A. J. and Parkes E. J., The N-soliton solution of the modified generalised Vakhnenko equation (a new nonlinear evolution equation), Chaos, Solitons & Fractals. (2003) 16, no. 1, 13–26, https://doi.org/10.1016/S0960-0779(02)00314-4, MR1941153.
10.1016/S0960-0779(02)00314-4
Web of Science® Google Scholar
9 Espinosa A. and Fujioka J., Hydrodynamic foundation and Painlevé analysis of Hirota-Satsuma-type equations, Journal of the Physical Society of Japan. (1994) 63, no. 4, 1289–1294, https://doi.org/10.1143/JPSJ.63.1289, MR1280384, ZBL0972.35514.
10.1143/JPSJ.63.1289
Web of Science® Google Scholar
10 Ablowitz M. J., Kaup D. J., Newell A. C., and Segur H., The inverse scattering transform-Fourier analysis for nonlinear problems, 1974, 53, no. 4, 249–315, MR0450815, ZBL0408.35068.
Google Scholar
11 Hirota R. and Satsuma J., N-soliton solutions of model equations for shallow water waves, 1976, 40, no. 2, 611–612, MR0397205, https://doi.org/10.1143/JPSJ.40.611.
10.1143/JPSJ.40.611
Google Scholar
12 Morrison A. J. and Parkes E. J., The N-soliton solution of a generalised Vakhnenko equation, Glasgow Mathematical Journal. (2001) 43A, 65–90, Integrable systems: linear and nonlinear dynamics (Islay, 1999)https://doi.org/10.1017/S0017089501000076, MR1869687.
10.1017/S0017089501000076
Web of Science® Google Scholar
13 Liu Y., Li Z., and Wang K., Symbolic computation of exact solutions for a nonlinear evolution equation, Chaos, Solitons & Fractals. (2007) 31, no. 5, 1173–1180, https://doi.org/10.1016/j.chaos.2005.09.055, MR2261484, ZBL1139.35088.
10.1016/j.chaos.2005.09.055
Web of Science® Google Scholar
14 Xie S. and Cai J., Exact compacton and generalized kink wave solutions of the extended reduced Ostrovsky equation, Communications in Nonlinear Science and Numerical Simulation. (2009) 14, no. 9-10, 3561–3573, https://doi.org/10.1016/j.cnsns.2009.02.001, MR2509948, ZBL1221.35378.
10.1016/j.cnsns.2009.02.001
Web of Science® Google Scholar
15 Stepanyants Y. A., Solutions classification to the extended reduced Ostrovsky equation, SIGMA. (2008) 4, article 073, 1–19, https://doi.org/10.3842/SIGMA.2008.073, MR2470523, ZBL1169.35378.
10.3842/SIGMA.2008.073
Google Scholar
16 Song M., Application of bifurcation method to the generalized Zakharov equations, Abstract and Applied Analysis. (2012) 2012, 8, 308326, MR2994924, ZBL1259.35058.
10.1155/2012/308326
Google Scholar
17 Song M., Bouthina S. A., and Biswas A., Topological soliton solution and bifurcation analysis of the Klein-Gordon-Zakharov equation in (1 + 1)-dimensions with power law nonlinearity, Journal of Applied Mathematics. (2013) 2013, 7, https://doi.org/10.1155/2013/972416, 972416.
10.1155/2013/972416
Google Scholar
18 Biswas A. and Song M., Soliton solution and bifurcation analysis of the Zakharov-Kuznetsov-Benjamin-Bona-Mahoney equation with power law nonlinearity, Communications in Nonlinear Science and Numerical Simulation. (2013) 18, 1676–1683.
10.1016/j.cnsns.2012.11.014
Web of Science® Google Scholar
19 Song M., Yang C., and Zhang B., Exact solitary wave solutions of the Kadomtsov-Petviashvili-Benjamin-Bona-Mahony equation, Applied Mathematics and Computation. (2010) 217, no. 4, 1334–1339, https://doi.org/10.1016/j.amc.2009.05.007, MR2727370, ZBL1203.35245.
10.1016/j.amc.2009.05.007
Web of Science® Google Scholar
20 Zhang B.-G., Liu Z.-R., and Xiao Q., New exact solitary wave and multiple soliton solutions of quantum Zakharov-Kuznetsov equation, Applied Mathematics and Computation. (2010) 217, no. 1, 392–402, https://doi.org/10.1016/j.amc.2010.05.074, MR2672599, ZBL1200.35238.
10.1016/j.amc.2010.05.074
Web of Science® Google Scholar
21 Zhang B.-G., Li S.-Y., and Liu Z.-R., Homotopy perturbation method for modified Camassa-Holm and Degasperis-Procesi equations, Physics Letters A. (2008) 372, no. 11, 1867–1872, https://doi.org/10.1016/j.physleta.2007.10.072, MR2398391, ZBL1220.34010.
10.1016/j.physleta.2007.10.072
CAS Web of Science® Google Scholar
22 Li J. and Chen F., Exact travelling wave solutions and their dynamical behavior for a class coupled nonlinear wave equations, Discrete and Continuous Dynamical Systems. Series B. (2013) 18, no. 1, 163–172, MR2982012.
10.3934/dcdsb.2013.18.163
Web of Science® Google Scholar
23 Li J., Existence of exact families of traveling wave solutions for the sixth-order Ramani equation and a coupled Ramani equation, International Journal of Bifurcation and Chaos in Applied Sciences and Engineering. (2012) 22, no. 1, 2, 1250002, https://doi.org/10.1142/S0218127412500022, MR2901776.
10.1142/S0218127412500022
Web of Science® Google Scholar
24 Pan C. and Liu Z., Further results on the traveling wave solutions for an integrable equation, Journal of Applied Mathematics. (2013) 6, 681383, MR3035172, ZBL1266.37032.
Google Scholar
25 Liu Z. and Liang Y., The explicit nonlinear wave solutions and their bifurcations of the generalized Camassa-Holm equation, International Journal of Bifurcation and Chaos in Applied Sciences and Engineering. (2011) 21, no. 11, 3119–3136, https://doi.org/10.1142/S0218127411030556, MR2871965, ZBL1258.35050.
10.1142/S0218127411030556
Web of Science® Google Scholar
26 Chen H.-T., Yang S.-H., and Ma W.-X., Double sub-equation method for complexiton solutions of nonlinear partial differential equations, Applied Mathematics and Computation. (2013) 219, no. 9, 4775–4781, https://doi.org/10.1016/j.amc.2012.10.094, MR3001525.
10.1016/j.amc.2012.10.094
Google Scholar
27 Ma W.-X. and Liu Y., Invariant subspaces and exact solutions of a class of dispersive evolution equations, Communications in Nonlinear Science and Numerical Simulation. (2012) 17, no. 10, 3795–3801, https://doi.org/10.1016/j.cnsns.2012.02.024, MR2916434, ZBL1250.35057.
10.1016/j.cnsns.2012.02.024
Web of Science® Google Scholar
28 Wang M., Li X., and Zhang J., The (G^′/G)-expansion method and travelling wave solutions of nonlinear evolution equations in mathematical physics, Physics Letters A. (2008) 372, no. 4, 417–423, https://doi.org/10.1016/j.physleta.2007.07.051, MR2381823.
10.1016/j.physleta.2007.07.051
CAS Web of Science® Google Scholar
29 Wang M., Zhang J., and Li X., Application of the (G^′/G)-expansion to travelling wave solutions of the Broer-Kaup and the approximate long water wave equations, Applied Mathematics and Computation. (2008) 206, no. 1, 321–326, https://doi.org/10.1016/j.amc.2008.08.045, MR2474977.
10.1016/j.amc.2008.08.045
Web of Science® Google Scholar
30 Ganji D. D. and Abdollahzadeh M., Exact traveling solutions of some nonlinear evolution equation by (G^′/G)-expansion method, Journal of Mathematical Physics. (2009) 50, no. 1, 013519, https://doi.org/10.1063/1.3052847, MR2492629.
10.1063/1.3052847
Web of Science® Google Scholar
31 Zhou Y.-B. and Li C., Application of modified G^′/G-expansion method to traveling wave solutions for Whitham-Broer-Kaup-like equations, Communications in Theoretical Physics. (2009) 51, no. 4, 664–670, https://doi.org/10.1088/0253-6102/51/4/17, MR2567269.
10.1088/0253-6102/51/4/17
Web of Science® Google Scholar
32 Zhang H., New application of the (G^′/G)-expansion method, Communications in Nonlinear Science and Numerical Simulation. (2009) 14, 3220–3225.
10.1016/j.cnsns.2009.01.006
Web of Science® Google Scholar
33 Zhang S., Tong J. L., and Wang W., A generalized (G^′/G)-expansion method for the mKdV equation with variable coefficients, Physics Letters A. (2008) 372, 2254–2257.
10.1016/j.physleta.2007.11.026
CAS Web of Science® Google Scholar
34 Zhang J., Wei X., and Lu Y., A generalized (G^′/G)-expansion method and its applications, Physics Letters A. (2008) 372, no. 20, 3653–3658, https://doi.org/10.1016/j.physleta.2008.02.027, MR2413864.
10.1016/j.physleta.2008.02.027
CAS Web of Science® Google Scholar
35 Li W. A., Chen H., and Zhang G. C., The (ω/g)-expansion method and its application to Vakhnenko equation, Chinese Physics B. (2009) 18, 400–405.
10.1088/1674-1056/18/2/004
CAS Web of Science® Google Scholar
36 Ma W. X. and Fuchssteiner B., Explicit and exact solutions to a Kolmogorov-Petrovskii-Piskunov equation, International Journal of Non-Linear Mechanics. (1996) 31, no. 3, 329–338, https://doi.org/10.1016/0020-7462(95)00064-X, MR1395482, ZBL0863.35106.
10.1016/0020-7462(95)00064-X
Web of Science® Google Scholar
37 Ma W.-X. and Lee J.-H., A transformed rational function method and exact solutions to the 3 + 1 dimensional Jimbo-Miwa equation, Chaos, Solitons & Fractals. (2009) 42, no. 3, 1356–1363, https://doi.org/10.1016/j.chaos.2009.03.043, MR2547030, ZBL1198.35231.
10.1016/j.chaos.2009.03.043
Web of Science® Google Scholar
38 Ma W.-X. and Zhu Z., Solving the (3 + 1)-dimensional generalized KP and BKP equations by the multiple exp-function algorithm, Applied Mathematics and Computation. (2012) 218, no. 24, 11871–11879, https://doi.org/10.1016/j.amc.2012.05.049, MR2945190.
10.1016/j.amc.2012.05.049
Web of Science® Google Scholar
39 Vakhnenko V. O. and Parkes E. J., The two loop soliton solution of the Vakhnenko equation, Nonlinearity. (1998) 11, no. 6, 1457–1464, https://doi.org/10.1088/0951-7715/11/6/001, MR1660356, ZBL0914.35115.
10.1088/0951-7715/11/6/001
Web of Science® Google Scholar

Citing Literature

All articles

Analytical and Multishaped Solitary Wave Solutions for Extended Reduced Ostrovsky Equation

Abstract

1. Introduction

2. Description of the Modified (G^′/G)-Expansion Method

3. Exact Traveling Wave Solutions of the Extended Reduced Ostrovsky Equation

4. Multishaped Solitary Wave Solutions

5. Conclusion

Acknowledgment

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Analytical and Multishaped Solitary Wave Solutions for Extended Reduced Ostrovsky Equation

Abstract

1. Introduction

2. Description of the Modified (G′/G)-Expansion Method

3. Exact Traveling Wave Solutions of the Extended Reduced Ostrovsky Equation

4. Multishaped Solitary Wave Solutions

5. Conclusion

Acknowledgment

References

Citing Literature

Figures

References

Related

Information

2. Description of the Modified (G^′/G)-Expansion Method