Volume 2013, Issue 1 646407

Research Article

Open Access

Effect of Varying Illumination and Temperature on Steady-State and Dynamic Parameters of Dye-Sensitized Solar Cell Using AC Impedance Modeling

Brijesh Tripathi,

Brijesh Tripathi

School of Technology, Pandit Deendayal Petroleum University, Gandhinagar 382007, India pdpu.ac.in

School of Solar Energy, Pandit Deendayal Petroleum University, Gandhinagar 382007, India pdpu.ac.in

Search for more papers by this author

Pankaj Yadav,

Pankaj Yadav

School of Solar Energy, Pandit Deendayal Petroleum University, Gandhinagar 382007, India pdpu.ac.in

Search for more papers by this author

Manoj Kumar,

Corresponding Author

Manoj Kumar

[email protected]

orcid.org/0000-0002-2933-0594

School of Technology, Pandit Deendayal Petroleum University, Gandhinagar 382007, India pdpu.ac.in

Search for more papers by this author

Brijesh Tripathi,

Brijesh Tripathi

School of Technology, Pandit Deendayal Petroleum University, Gandhinagar 382007, India pdpu.ac.in

School of Solar Energy, Pandit Deendayal Petroleum University, Gandhinagar 382007, India pdpu.ac.in

Search for more papers by this author

Pankaj Yadav,

Pankaj Yadav

School of Solar Energy, Pandit Deendayal Petroleum University, Gandhinagar 382007, India pdpu.ac.in

Search for more papers by this author

Manoj Kumar,

Corresponding Author

Manoj Kumar

[email protected]

orcid.org/0000-0002-2933-0594

School of Technology, Pandit Deendayal Petroleum University, Gandhinagar 382007, India pdpu.ac.in

Search for more papers by this author

First published: 29 August 2013

https://doi.org/10.1155/2013/646407

Citations: 22

Academic Editor: Wayne A. Anderson

Share a link

Email
Wechat
Bluesky

Abstract

The steady-state current-voltage curve and dynamic response of a dye-sensitized solar cell (DSSC) is mathematically modeled based on electrical equivalent circuit. The effect of temperature and illumination on the steady-state and dynamic parameters of dye-sensitized solar cells is studied. It is found that the dynamic resistance of DSSC decreases from 619.21 Ω to 90.34 Ω with the increase in illumination level from 200 W/m² to 800 W/m². A positive temperature coefficient of dynamic resistance is observed. The interfacial charge transfer and recombination losses at the oxide/dye/electrolyte interface are found to be the most influential factor on the overall conversion efficiency and included in the mathematical model. The saturation current of rectifying diode and saturation current of recombination diode are responsible for the transfer recombination losses and have major influence on the overall conversion efficiency.

1. Introduction

In recent years, dye-sensitized solar cells (DSSCs) have attracted much attention as a potential low-cost alternative to single or polycrystalline p-n junction-based silicon solar cells. Various oxide-based materials such as NiO₂, Fe₂O₃, ZnO, SnO₂, and TiO₂ have been studied for photoelectrochemical [1–3] and photovoltaic [4, 5] applications. Tiwana et al. have shown that TiO₂ is better material, based on their studies on electron mobility and injection dynamics in mesoporous films for DSSCs [4]. Recent study by Burschka et al. [5] has shown a power conversion efficiency of 15% for the solid-state TiO₂ mesoscopic solar cells based on perovskite absorber. When DSSC is illuminated, photons are absorbed by dye molecules, which inject electrons from their excited states into the conduction band of the TiO₂ nanoparticles to leave the dye molecule oxidized. Oxidized dye molecules are reduced by a redox electrolyte, which transports the positive charges by diffusion to a Pt back electrode. Efficient electron injection from excited state of the dye to TiO₂ plays an important role in DSSC [6, 7]. The injected electrons flow through the porous TiO₂ thin film to the transparent conducting oxide (TCO), depending on the incident intensity and trapping-detrapping effect [8–11]. Subsequently, the electrons flow to the back electrode via the external circuit. The oxidized dye molecules are regenerated by redox mediators (). Finally, the oxidized redox mediators () are transported to the back electrode where regeneration of redox mediators occurs for a complete DSSC operation cycle [12, 13].

Usually the dye molecules have low absorption coefficient. The low absorption coefficient of a dye monolayer is compensated by the mesoporous structure of the TiO₂ film, which leads to a strong increase in the number of TiO₂/dye/electrolyte interfaces through which photons pass, thus increasing the absorption probability. This phenomenon uses the increased surface area due to associated porosity of the TiO₂ layer. In fact, studies on the DSSC electrode morphology showed that the light absorption coefficient α and electron transport coefficient D varied with porosity P [14–27]. The influence of electrode morphology, interfacial charge recombination, and the charge transport on the output performance of DSSC is also studied by electrochemical impedance spectroscopy (EIS) [28–30]. Electrochemical impedance spectroscopy is a steady-state method of measuring the current response to the application of an AC voltage as a function of the frequency to study the kinetics of electrochemical and photoelectrochemical behaviors of devices. This paper presents a theoretical EIS and I-V model to estimate steady-state and dynamic parameters of dye-sensitized solar cell. The developed theoretical model is validated with reported experimental results. The effect of temperature and illumination on the steady-state and dynamic parameters is systematically studied for a dye-sensitized solar cell. The existing steady-state models of dye-sensitized solar cells represent the steady-state characteristics of the solar cells but there exists a limitation in predicting dynamic characteristics such as the response of the solar cell on the AC components. For the design of a high performance power conditioning unit, it is essential to have accurate information about the static and dynamic characteristics of the solar cell.

2. Performance Prediction Model

2.1. Prediction of I-V Curve of DSSC

An operating DSSC is principally governed by the relative kinetic rates of several charge transfer steps. The charge transfer taking place from excited dye to TiO₂ nanoparticle, from electrolyte to the dye, and from TiO₂ to the load terminals plays very critical role in the performance of DSSC. Thus, it is very important to understand all the electronic processes taking place at the TiO₂ nanoparticles level, as well as the dynamics of charge separation and charge transport at the metal/oxide interface. The schematic band diagram of dye-sensitized solar cell is shown in Figure 1, which illustrates the following sequence of electron transfer and charge-transport processes, which are at the basis of a DSC’s operation mode [28]:

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Band diagram and electron transport in dye-sensitized solar cell.

Electron excitation

()

Electron injection into the CB

()

Dye generation

()

Electrolyte regeneration at the CE

()

In addition to the frontward electron transfer and transport processes, Figure 1 also illustrates several challenging backward electron loss pathways, including

Fall to ground state

()

Regeneration of dye by injected electron

()

Recombination of injected electrons with

()

Since in DSSCs the function of light absorption is separated from the charge carrier transport, the dye should have a broad absorption spectrum in order to harvest maximum amount of solar radiation. The excited state of the dye must energetically lie above the conduction band edge of the TiO₂ nanoparticles to assure fast electron injection, before it can fall back to its ground state [31]. On the other hand, the oxidized dye must have a higher positive potential than the redox couple in the electrolyte. Thus, the regeneration of the dye by the redox electrolyte must be extremely fast compared with the recombination of the injected electrons with the oxidized dye.

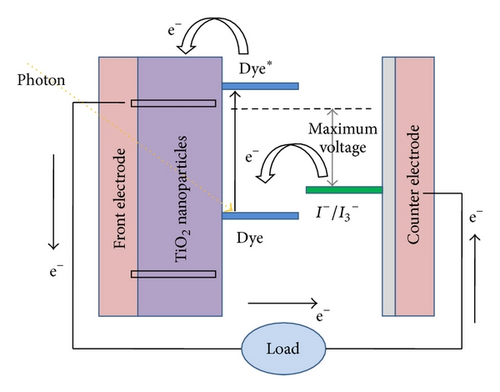
The redox electrolyte is responsible for the dye regeneration, becoming oxidized by electron injection to the TiO₂ conduction band. Moreover, the electrolyte conducts the positive charges (holes) to the counter electrode, where the redox-couple itself is regenerated. As the open-circuit voltage of the system corresponds to the difference between the redox potential of the electrolyte and the TiO₂ Fermi level, the redox potential must be as positive as possible in order to assure high open-circuit voltages. Moreover, to overcome the problem related to slow charge-transfer reaction at the counter-electrode, a platinum-based catalyst must be employed. On the other hand, the overvoltage at the semiconductor/dye interface should be high since the dark current caused by electron back transfer to the electrolyte decreases the number of electrons available for photocurrent.

Under a steady-state condition of illuminated DSSC, the electron injection from excited dye molecules, transport in the mesoporous semiconductor (TiO₂) thin film, and recombination with electrolyte at the TiO₂/electrolyte interface can be described by the following electron diffusion differential equation [25–27]:

()

where n(x) is the excessive electron concentration at position x inside the mesoporous TiO₂ thin layer; n₀ is the electron concentration under a dark condition (n₀ = 10¹⁶ cm⁻³) [16, 17]; τ is the lifetime of the conduction band-free electrons; Φ₀ is the incident irradiation intensity; α is the light absorption coefficient of the mesoporous TiO₂ thin layer; and D is the electron diffusion coefficient. The effect due to transport of

redox electrolyte is neglected because the pore sizes in DSSC are normally greater than or comparable to 14 nm [22]. In a steady-state, trapping-detrapping in the electron transport can be neglected, and hence the electron lifetime τ is assumed to be constant in a DSSC [24, 26]. The general solution of (8) in terms of I-V relationship, with the short-circuit current and open-circuit voltage boundary conditions, can be expressed as follows:

()

where I_ph is the photogenerated current, λ is the incident light in W/m², I_i and I_r are the saturation current densities of the rectifying and recombination diodes, respectively, k_B is the Boltzmann constant, T is the absolute temperature, T_C is the cell temperature and T_Ref is the reference temperature (≈298.14 K), q is the electron charge, ω is the angular frequency, σ is the Warburg coefficient, L_n is the electron diffusion length equal to

, d is the mesoporous TiO₂ layer thickness, and A is the area of the DSSC; a is equal to 4 × 10⁻⁴ cm² s⁻¹; μ is equal to 0.82; and critical porosity P_C is equal to 0.76.

The photocurrent (I_ph) mainly depends on the solar insolation and cell’s working temperature. The saturation current of a solar cell varies with the cell temperature, which is described by (8):

()

Reverse saturation current of the cell at reference temperature depends on the open-circuit voltage (V_OC) and can be approximately obtained by the following equation as given by Tsai et al. [32]:

()

Based on the theoretical model described above, the DSSC is simulated using MATLAB/Simulink.

2.2. Prediction of Dynamic Resistance of DSSC

Due to the nonlinear I-V characteristics curve of the DSSCs, it is difficult to analyze and determine their output impedance, that is, dynamic resistance. It is necessary to develop an efficient method to determine the dynamic resistance that corresponds to maximum power point (MPP) of DSSC. Being the dynamic quantity, the dynamic resistance is determined by the derivative of the I-V characteristics of the cell and is defined as the change in voltage divided by the change in current (dV_m/dI_m) at MPP. In addition to this, the dynamic resistance is composed of series resistance and shunt resistance. A DSSC mainly consists of three types of resistances: series resistance (R_S), shunt resistance (R_sh), and dynamic resistance (R_d) as shown in Figure 2. The series resistance R_S can be determined by various illumination conditions such as dark, constant illumination, and varying illumination, and they yield different results [33]. Practically, R_S is determined by using two different illumination levels, the so-called two-curve method. Shunt resistance, R_sh, can be obtained from only one illuminated I-V curve or single curve method. The output impedance of solar PV module, that is, dynamic resistance, is usually composed of the series resistance and shunt resistance.

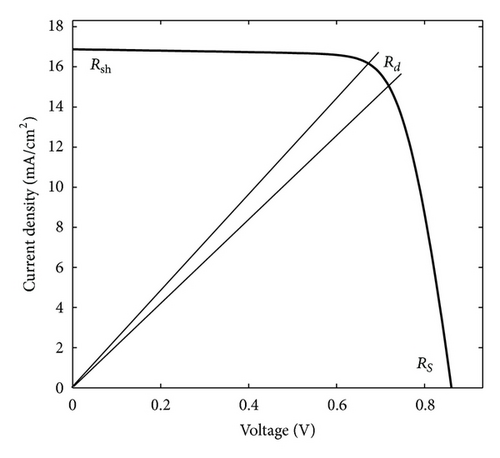
In order to estimate components of resistance offered by DSSC, a new and simple method is proposed here based on the equivalent circuit of DSSC shown in Figure 3. Using this method the dynamic resistance of the DSSC can be determined from single I-V characteristics curve under illumination. The model of the dynamic resistance with the combination of the finite series resistance and shunt resistance is also taken into consideration. Through the developed model, the effect of light intensity and temperature on the I-V characteristics and dynamic resistance of the DSSC is studied.

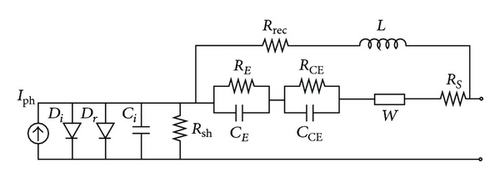
A standard DSSC consists of three interfaces formed by FTO/TiO₂, TiO₂/dye/electrolyte, and electrolyte/Pt-FTO represented by an equivalent circuit shown in Figure 3 [34]. The interfacial charge transfer at the TiO₂/dye/electrolyte is characterized by a rectifying diode D_i and a double-layer capacitance C_i. A recombination diode D_r with an ideality factor, m, is employed to denote the interfacial charge recombination losses to both the dye cation and the redox electrolyte. A shunt resistance R_sh takes into account all parallel resistive losses across the photovoltaic device including leakage current. The photogenerated current I_ph is in parallel with the rectifying diode. An inductive recombination pathway on account of charge-transfer current [34] is incorporated into the circuit, consisting of a recombination resistance (R_rec) in series with an inductor (L). The charge-transfer resistance and interfacial capacitance at the FTO electrode and electrolyte/Pt-FTO interfaces are characterized by R_E and C_E and R_CE and C_CE, respectively. The Nernst diffusion of the carrier transport by ions within the electrolyte is denoted by the Warburg impedance (W). A resistance element R_S represents the bulk and contact resistive losses present in a DSSC, such as the sheet resistance of the FTO glass.

The terminal equation for current and voltage of the DSSC based on two-diode model (9) can be modified under the static condition (ω ≈ 0) as follows [34]:

()

Equation (21) is rearranged, and the modified equation is given by,

()

In order to estimate the dynamic resistance equation (21) is subjected to the following boundary conditions:

(1)
0 < V < V_m and I_m < I < I_SC;
(2)
V_m < V < V_OC and 0 < I < I_m.

For first boundary condition, I_r ≫ I_i, so (22) can be rearranged as

()

From (23), the voltage across a load at one illumination level is given as

()

At any two operating points (V₁, I₁) and (V_m, I_m) on a single I-V curve, the relationship between V and I is:

()

For second boundary condition, I_r ≪ I_i, so (22) can be rearranged as

()

From (13), the voltage across a load at one illumination level is given as

()

At any two operating points (V_m, I_m) and (V₂, I₂) on a single I-V curve, the relationship between V and I is

()

From (25)–(28), the Z can be rewritten as

()

Equation (29) can be simplified as a shunt resistance is normally much greater than series impedance Z. Thus R_sh[I_ph + I_i + I_r − I₁] ≫ I₁Z and R_sh[I_ph + I_i + I_r − I₂] ≫ I₂Z. Therefore,

()

The first term of (30) is essentially a slope at any operating point or external dynamic resistance, R_D. The second term is the internal dynamic resistance, R_d, of the DSSC.

For the open-circuit condition and short-circuit conditions DSSC, the following two expressions are given using the slope of one I-V characteristic at the points (V_OC, 0) and (0, I_SC) by

()

respectively. The dynamic resistance increases with the increase in temperature because of marginal increase in short-circuit current [35–38].

3. Validation and Analysis of Developed Model

3.1. Current-Voltage Characterization

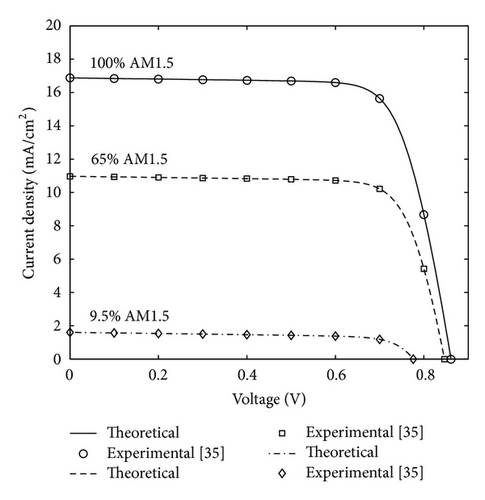
Current-voltage (I-V) characterization is very significant technique to study nonlinear response of the DSSC under dark and illuminated conditions. The simulated I-V characteristic of DSSC was experimentally validated by comparison with data from Gratzel [39] as shown in Figure 4.

The input data used for simulation purposes are compiled in Table 1.

Table 1. Values of model parameters used in simulated I-V curves and the Nyquist plots [32].

I_ph

(mA/cm²)

I_i

(A/cm²)

I_r

(A/cm²)

C_i

(F)

R_sh

(F)

R_rec

(Ω)

R_E

(Ω)

C_E

(mF)

R_CE

(Ω)

C_CE

(μF)

(Ω s^−1/2)

R_S

(Ω)

16.9

0.4 × 10⁻¹⁶

1.4 × 10⁻¹⁰

3000

4.2

21.7

0.8

9.8

4.2

12.6

It is evident from Figure 4 that the outlined model agrees quite well with the experimental data. The reported cell’s efficiency of 11.04% (J_SC = 16.9 mA/cm²; V_OC = 862 mV; P_MAX = 11.04 mW; R_S = 12.6 Ω) [39] is in straight agreement with the simulated parameters of the DSSC having efficiency of 10.85% (J_SC = 16.9 mA/cm²; V_OC = 862 mV; P_MAX = 10.85 mW; R_S = 10.85 Ω). The experimental and simulated I-V curves were fitted by means of the parameters R_S, R_sh, D_i, and D_r.

The curves at 0.65 sun and 0.1 sun were subsequently calculated using the same parameter as used at 1 sun, by only changing the light intensity in the simulation (i.e., the recombination constant and the quantum injection yield are taken to be independent of light intensity). It can be seen that short-circuit current, maximum power point and open-circuit voltage are in general agreement with the experimental results.

3.2. Electrochemical Impedance Spectroscopy

Electrochemical impedance spectroscopy is a technique extensively used for characterizing the electrical behavior of systems in which overall performance is determined by a number of strongly coupled processes, each taking place at a different rate. The most common and standard procedure in impedance measurements consists of applying a small sinusoidal voltage perturbation and monitoring the resulting current response of the system at the corresponding frequency. The single-frequency voltage perturbation is usually done at open-circuit conditions with magnitude V₀ of the modulation signal [41]:

()

The current response has the same period as the voltage perturbation but will be phase shifted by ϕ:

()

V₀ and I₀ are the amplitudes of the voltage and current signals, respectively, and ω is the radial frequency in radians per second.

In the Nyquist plots, the respective electrochemical steps with different time constants are represented by the semicircles as shown in Figure 5. Three semicircles correspond to three interfaces formed by FTO/TiO₂, TiO₂/dye/electrolyte, and electrolyte/Pt-FTO [39, 40, 42]. The tri-iodide diffusivity was obtained by fitting the experimental EIS spectra under illumination to an appropriate electrical analogue [43, 44]. The diffusion of in the electrolyte is usually well described by the Nernst diffusion impedance, characterized by the Warburg parameter and a characteristic diffusion time constant [45, 46]. Due to excess of I⁻ ions compared to , the former does not contribute to the diffusion impedance [47].

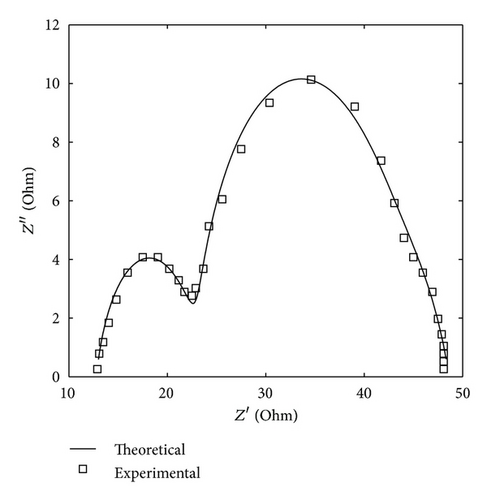
The low-frequency semiarc in the Nyquist plot represents the electrolyte-platinum interface and may be expressed as a charge-transfer resistance and a double-layer capacitance [34]. Impedance spectra are simulated over a frequency range of 0.01–10⁶ Hz with AC amplitude of 10 mV. The values of model parameters used in the simulation are summarized in Table 1. The shunt resistance, R_sh, can be estimated from the slope of the I-V curve near short-circuit current point, which is typically of order of 10³ for a highly efficient solar cell. The values of I_i and I_r are found to be of orders 10⁻¹⁵ and 10⁻¹⁰ A/cm², respectively. The inductor L is 10–100 H [48]. The double-layer capacitance, C_i, is determined to be of order 10 F. The large capacitance value at the TiO₂/dye/electrolyte interface (C_i) is likely to result from the large surface area of the nanocrystalline TiO₂ structure [30]. The length between the intercepts at the real axis corresponds to the charge-transfer resistance (R_ct) of the component. The double-layer capacitance (C_i) is determined from the characteristic frequency [49]. The resistance elements R_rec, R_E, R_CE, and R_S are typically of several ohms for a highly efficient solar cell. The interfacial capacitances C_E and C_CE are of orders 1 mF and 1 µF, respectively.

4. Results and Discussion

4.1. Effect of Illumination on Steady and Dynamic Parameters

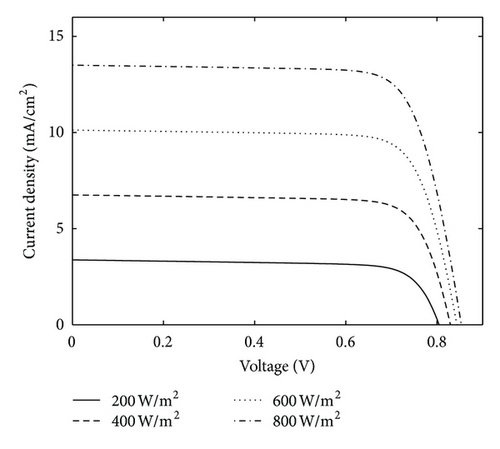
The proposed model in Section 2 is used to estimate the I-V characteristics of the DSSC. The static parameters (I_SC, V_OC, P_MAX, and R_S) of the DSSC are estimated in STC conditions. The simulated current-voltage characteristic of DSSC is shown in Figure 8 with varying illumination at constant cell temperature. Generally, the output current of the DSSC increases with the radiation intensity. A positive increment in current is mainly due to increase in solar irradiance. With the increase in the solar irradiance the higher number of photons strikes the DSSC which results in enhanced dye excitation and electron transfer into the conduction band of TiO₂ electrode resulting in higher photocurrent.

The values of the dynamic resistance at MPP are computed using the values of I_ph, I_SC, and R_S. The dynamic resistance of the DSSC is calculated in an effective manner using (30) as listed in Table 2. From the obtained theoretical data as listed in Table 2, the series resistance, R_S, shows a decreasing trend continuously with increase in the intensity of illumination. Using our previous work [50], the dynamic resistance of the DSSC can be determined for a given photogenerated current-voltage characteristic curve. The dynamic resistance for various illumination levels is listed in Table 2.

Table 2. Effect of illumination on steady-state and dynamic parameters of DSSC at 298.14 K.

Illumination (W/m²)	J_SC (mA/cm²)	V_OC (mV)	P_MAX (mW)	R_S (Ω)	R_d (Ω)	Efficiency, η (%)
200	3.4	804.7	2.0	38.28	619.21	10.00
400	6.8	829.5	4.3	18.52	306.55	10.75
600	10.1	843.7	6.6	12.4	148.94	11.00
800	13.5	853.6	8.8	9.66	90.34	11.00

The calculated values of dynamic resistance of the DSSC show strong dependence on solar radiation. The decrease in the dynamic resistance with increase in solar radiation is attributed to the decreased R_S. This is primarily caused by logarithmic increase in V_OC and a linear increase in DSSC photocurrent with increasing illumination. The plot shown in Figure 6 and extracted data listed in Table 2 show the illumination intensity dependence of I_SC, V_OC, and P_MAX. It is observed that the output power of the DSSC increases with the radiation intensity. Such an increase in output power is primarily caused by increase in V_OC and also due to the linear increase in I_SC. The linear boost in I_SC is attributed to the increased dye-photon interaction and enhanced number of carrier injections from the excited dye molecules to the conduction band of TiO₂ electrode. An exponential dependence of V_OC on illumination is observed in the DSSC. A similar study is reported by other researchers, and the relationship governing dependence of V_OC on light intensity is given by [51]

()

The open-circuit voltage, V_OC, is dependent on the saturation current density of recombination diode as given by (19) and (20). The open-circuit voltage, V_OC, is found to be increasing with increase in illumination intensity as shown in Figure 6. From this study it is evident that the saturation current density of the recombination diode (I_r) is independent of the illumination intensity. This is mainly due to insignificant change in the transport recombination magnitude which governs the electron transport process occurring either at the TiO₂ nanoparticle interfaces or at the electrode-electrolyte interface [51].

4.2. Effect of DSSC’s Working Temperature on Steady and Dynamic Parameters

The effect of the cell temperature (T_C) on I-V curve of DSSC is estimated from the proposed model as shown in Figure 7, and the extracted steady-state and dynamic parameters are listed in Table 3.

Table 3. Effect of temperature on steady-state and dynamic parameters of DSSC at 800 W/m².

Temperature (K)	J_SC (mA/cm²)	V_OC (mV)	P_MAX (mW)	R_S (Ω)	R_d (Ω)	Efficiency, η (%)	I_r (A/m²)	I_i (A/m²)
298	13.5	853.6	8.8	9.66	90.34	11.00	3.22 × 10⁻⁷	1.04 × 10⁻¹³
303	13.5	827.4	8.5	10.05	96.77	10.62	5.84 × 10⁻⁷	3.41 × 10⁻¹³
308	13.6	801.2	8.1	10.45	102.95	10.12	1.04 × 10⁻⁶	1.08 × 10⁻¹²
313	13.6	774.9	7.8	10.88	108.64	9.75	1.82 × 10⁻⁶	3.31 × 10⁻¹²

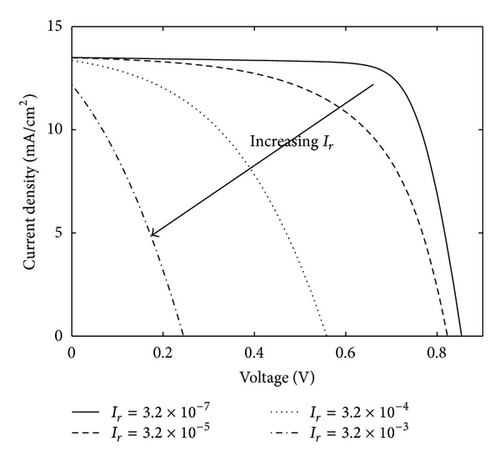
As the device temperature increases, negligible increase in short-circuit current is observed; however, the open-circuit voltage rapidly decreases due to the exponential dependence of the reverse saturation current on the cell temperature as given by (20) [50]. As a result of increased cell temperature, higher series resistance offers greater resistive power losses equivalent to I²R_S and thus reduces its performance by reducing efficiency. The increase in R_S causes maximum power point shifts towards lower values. The current output of the DSSC in the range of I_SC to I_MAX is dependent on the R_sh of the solar cells. For this study sufficiently high R_sh is considered for modeling (and the experimental value of R_sh is also quite high), so there is negligible variation in the current between I_SC and I_MAX with respect to varying voltage at the output terminal of DSSC. The voltage output of DSSC in the range of V_MAX to V_OC is dependent on series resistance. Although both resistances (R_S and R_sh) contribute to the degradation of the I-V curve, but the effect of R_S is dominant because the current loss (~I²R_S) is directly dependent on R_S. At higher current, in the case of DSSC, the loss term is more prominent. A decrease in the P_MAX with the increase in T_C is observed because as temperature increases the band gap of the TiO₂ semiconductor shrinks. The increased temperature causes reduction in open-circuit voltage (V_OC) and small increase in the photocurrent for a given irradiance because of fractional increase in the number of electrons transferred from valance band to conduction band of TiO₂ semiconductor. The excited state of the dye energetically lying above the conduction band edge of the TiO₂ nanoparticles assures fast electron injection, before it can fall back to its ground state. On the other hand, the oxidized dye has a higher positive potential than the redox-couple in the electrolyte. The redox electrolyte is responsible for the dye regeneration, becoming oxidized by electron injection to the TiO₂ conduction band. Further, the electrolyte conducts the positive charges (holes) to the counter-electrode, where the redox-couple itself is regenerated. As the open-circuit voltage of the system corresponds to the difference between the redox potential of the electrolyte and the TiO₂ Fermi level, the redox potential must be as positive as possible in order to assure high open-circuit voltages. As the temperature increases, the band gap of TiO₂ electrode shrinks which results in reduced difference between the redox potential of the electrolyte and the TiO₂ Fermi level and hence reduced V_OC. The similar trend of decreasing V_OC with increase in temperature is observed for DSSC by other researches [52]. Another significant factor which governs the decrease V_OC is the transfer recombination which occurs at the dye-electrode interface, electrolyte-dye interface, and electrolyte-counter electrode interface. The influence of each parameter on the overall conversion efficiency is simulated. It is clearly demonstrated that I_i (saturation current of rectifying diode) and I_r (saturation current of recombination diode) are responsible for the transfer recombination losses and have major influence on the overall conversion efficiency. However, the effect of resistive elements starts becoming dominant when the series resistance is getting larger, especially detrimental to the fill factor.

The effect of increase in the transfer recombination (which is related to recombination diode, D_r) is shown in Figure 8, wherein the increase in I_r plays a critical role in deciding the performance of DSSC.

It is noteworthy to mention that the saturation current (I_r) for recombination diode (D_r) in a two-diode model is mainly dependent on the cell temperature as given by (19). As the temperature increases, I_r increases, which further contributes to decline of the output performance of dye-sensitized solar cell (Figure 8).

5. Conclusions

A mathematical model that simulates the steady-state current-voltage curve and the dynamic response of a dye-sensitized solar cell (DSSC) based on equivalent circuit of DSSC is proposed. The interfacial charge transfer and recombination losses at the oxide/dye/electrolyte interface are found to be the most influential factor on the overall conversion efficiency and included in the mathematical model. All parameters in the model can be related to quantities accessible experimentally. The model predicts the dynamic current-voltage behavior of DSSC under varying illumination levels and temperatures. The implications of the model are discussed in terms of efficiencies potentially attainable in dye-sensitized solar cells having diffusional mechanism of charge transport.

Acknowledgment

The authors would like to acknowledge the scientific discussions held with Professor Indrajit Mukhopadhyay of School of Solar Energy, Pandit Deendayal Petroleum University, Gandhinagar.

References

1 Li J., Meng F., Suri S., Ding W., Huang F., and Wu N., Photoelectrochemical performance enhanced by a nickel oxide-hematite p-n junction photoanode, Chemical Communications. (2012) 48, no. 66, 8213–8215, https://doi.org/10.1039/c2cc30376k.
Google Scholar
2 Meng F., Li J., Cushing S. K., Bright J., Zhi M., Rowley J. D., Hong Z., Manivannan A., Bristow A. D., and Wu N., Photocatalytic water oxidation by hematite/reduced graphene oxide composites, ACS Catalysis. (2013) 3, no. 4, 746–751, https://doi.org/10.1021/cs300740e.
Google Scholar
3 Meng F., Li J., Cushing S. K., Zhi M., and Wu J N., Solar hydrogen generation by nanoscale p-n junction of p-type molybdenum disulfide/n-type nitrogen-doped reduced graphene oxide, Journal of the American Chemical Society. (2013) 135, no. 28, 10286–10289, https://doi.org/10.1021/ja404851s.
Google Scholar
4 Tiwana P., Docampo P., Johnston M. B., Snaith H. J., and Herz L. M., Electron mobility and injection dynamics in mesoporous ZnO, SnO₂, and TiO₂ films used in dye-sensitized solar cells, ACS Nano. (2011) 5, no. 6, 5158–5166, 2-s2.0-79959804926, https://doi.org/10.1021/nn201243y.
Web of Science® Google Scholar
5 Burschka J., Pellet N., Moon S. J., Humphry-Baker R., Gao P., Nazeeruddin M. K., and Gr?tzel M., Sequential deposition as a route to high-performance perovskite-sensitized solar cells, Nature. (2013) 499, 316–319, https://doi.org/10.1038/nature12340.
Web of Science® Google Scholar
6 Franco G., Gehring J., Peter L. M., Ponomarev E. A., and Uhlendorf I., Frequency-resolved optical detection of photoinjected electrons in dye-sensitized nanocrystalline photovoltaic cells, Journal of Physical Chemistry B. (1999) 103, no. 4, 692–698, 2-s2.0-0001096158.
Web of Science® Google Scholar
7 Cherepy N. J., Smestad G. P., Grätzel M., and Zhang J. Z., Ultrafast electron injection: implications for a photoelectrochemical cell utilizing an anthocyanin dye-sensitized TiO₂ nanocrystalline electrode, Journal of Physical Chemistry B. (1997) 101, no. 45, 9342–9351, 2-s2.0-0031556680.
Google Scholar
8 Peter L. M. and Wijayantha K. G. U., Intensity dependence of the electron diffusion length in dye-sensitised nanocrystalline TiO₂ photovoltaic cells, Electrochemistry Communications. (1999) 1, no. 12, 576–580, 2-s2.0-0001484761.
Google Scholar
9 Fredin K., Nissfolk J., and Hagfeldt A., Brownian dynamics simulations of electrons and ions in mesoporous films, Solar Energy Materials and Solar Cells. (2005) 86, no. 2, 283–297, 2-s2.0-10844240543, https://doi.org/10.1016/j.solmat.2004.07.010.
Google Scholar
10 Duffy N. W., Peter L. M., Rajapakse R. M. G., and Wijayantha K. G. U., A novel charge extraction method for the study of electron transport and interfacial transfer in dye sensitised nanocrystalline solar cells, Electrochemistry Communications. (2000) 2, no. 9, 658–662, 2-s2.0-0033790230, https://doi.org/10.1016/S1388-2481(00)00097-7.
Google Scholar
11 Peter L. M. and Wijayantha K. G. U., Electron transport and back reaction in dye sensitized nanocrystalline photovoltaic cells, Electrochimica Acta. (2000) 45, no. 28, 4543–4551, 2-s2.0-0034290820, https://doi.org/10.1016/S0013-4686(00)00605-8.
Google Scholar
12 Papageorgiou N., Gratzel M., and Infelta P. P., On the relevance of mass transport in thin layer nanocrystalline photoelectrochemical solar cells, Solar Energy Materials and Solar Cells. (1996) 44, no. 4, https://doi.org/10.1016/S0927-0248(96)00050-5.
Google Scholar
13 Imoto K., Takahashi K., Yamaguchi T., Komura T., Nakamura J.-I., and Murata K., High-performance carbon counter electrode for dye-sensitized solar cells, Solar Energy Materials and Solar Cells. (2003) 79, no. 4, 459–469, 2-s2.0-0042512227, https://doi.org/10.1016/S0927-0248(03)00021-7.
10.1016/S0927-0248(03)00021-7
Web of Science® Google Scholar
14 Van de Lagemaat J., Benkstein K. D., and Frank A. J., Relation between particle coordination number and porosity in nanoparticle films: implications to dye-sensitized solar cells, Journal of Physical Chemistry B. (2001) 105, no. 50, 12433–12436, 2-s2.0-0035924833, https://doi.org/10.1021/jp013369z.
Google Scholar
15 Benkstein K. D., Kopidakis N., Van de Lagemaat J., and Frank A. J., Influence of the percolation network geometry on electron transport in dye-sensitized titanium dioxide solar cells, Journal of Physical Chemistry B. (2003) 107, no. 31, 7759–7767, 2-s2.0-0043235646.
Web of Science® Google Scholar
16 Rothenberger G., Comte P., and Gratzel M., A contribution to the optical design of dye-sensitized nanocrystalline solar cells, Solar Energy Materials and Solar Cells. (1999) 58, no. 3, 321–336, https://doi.org/10.1016/S0927-0248(99)00015-X.
10.1016/S0927-0248(99)00015-X
Google Scholar
17 Ferber J. and Luther J., Computer simulations of light scattering and absorption in dye-sensitized solar cells, Solar Energy Materials and Solar Cells. (1998) 54, no. 1–4, 265–275, https://doi.org/10.1016/S0927-0248(98)00078-6.
Google Scholar
18 Wei-Wei X., Lin-Hua H., Song-Yuan D., Chang-Neng Z., Xiang-Dong L., and Wei-Ping J., A study on porosity distribution in nanoporous TiO₂ photoelectrodes for output performance of dye-sensitized solar cells, Chinese Physics Letters. (2010) 27, no. 3, 038202.
Google Scholar
19 Cass M. J., Qiu F. L., Walker A. B., Fisher A. C., and Peter L. M., Influence of grain morphology on electron transport in dye sensitized nanocrystalline solar cells, Journal of Physical Chemistry B. (2003) 107, no. 1, 113–119, 2-s2.0-0037426854, https://doi.org/10.1021/jp026798l.
Google Scholar
20 Wang Z. S., Kawauchi H., Kashima T., and Arakawa H., Significant influence of TiO₂ photoelectrode morphology on the energy conversion efficiency of N719 dye-sensitized solar cell, Coordination Chemistry Reviews. (2004) 248, no. 13-14, 1381–1389, https://doi.org/10.1016/j.ccr.2004.03.006.
Web of Science® Google Scholar
21 Nakade S., Saito Y., Kubo W., Kitamura T., Wada Y., and Yanagida S., Influence of TiO₂ nanoparticle size on electron diffusion and recombination in dye-sensitized TiO₂ solar cells, Journal of Physical Chemistry B. (2003) 107, no. 33, 8607–8611, 2-s2.0-0042471502.
Google Scholar
22 Saito Y., Kambe S., Kitamura T., Wada Y., and Yanagida S., Morphology control of mesoporous TiO₂ nanocrystalline films for performance of dye-sensitized solar cells, Solar Energy Materials and Solar Cells. (2004) 83, no. 1, 1–13, 2-s2.0-2342551123, https://doi.org/10.1016/j.solmat.2004.02.010.
Google Scholar
23 Barbé C. J., Arendse F., Comte P., Jirousek M., Lenzmann F., Shklover V., and Grätzel M., Nanocrystalline titanium oxide electrodes for photovoltaic applications, Journal of the American Ceramic Society. (1997) 80, no. 12, 3157–3171, 2-s2.0-0031360813.
Web of Science® Google Scholar
24 Ni M., Leung M. K. H., Leung D. Y. C., and Sumathy K., An analytical study of the porosity effect on dye-sensitized solar cell performance, Solar Energy Materials and Solar Cells. (2006) 90, no. 9, 1331–1344, 2-s2.0-33644989682, https://doi.org/10.1016/j.solmat.2005.08.006.
Google Scholar
25 Sodergren S., Hagfeldt A., Olsson J., and Lindquist S.-E., Theoretical models for the action spectrum and the current-voltage characteristics of microporous semiconductor films in photoelectrochemical cells, Journal of physical chemistry. (1994) 98, no. 21, 5552–5556, 2-s2.0-0028442312.
Google Scholar
26 Gomez R. and Salvador P., Photovoltage dependence on film thickness and type of illumination in nanoporous thin film electrodes according to a simple diffusion model, Solar Energy Materials and Solar Cells. (2005) 88, no. 4, 377–388, https://doi.org/10.1016/j.solmat.2004.11.008.
Google Scholar
27 Ni M., Leung M. K. H., and Leung D. Y. C., Theoretical modelling of the electrode thickness effect on maximum power point of dye-sensitized solar cell, The Canadian Journal of Chemical Engineering. (2008) 86, no. 1, 35–42, https://doi.org/10.1002/cjce.20015.
Google Scholar
28 Peter L., Transport, trapping and interfacial transfer of electrons in dye-sensitized nanocrystalline solar cells, Journal of Electroanalytical Chemistry. (2007) 599, no. 2, 233–240, 2-s2.0-33845951707, https://doi.org/10.1016/j.jelechem.2006.02.033.
Web of Science® Google Scholar
29 Bay L. and West K., An equivalent circuit approach to the modelling of the dynamics of dye sensitized solar cells, Solar Energy Materials and Solar Cells. (2005) 87, no. 1–4, 613–628, 2-s2.0-17644399100, https://doi.org/10.1016/j.solmat.2004.08.022.
Google Scholar
30 Dloczik L., Ileperuma O., Lauermann I., Peter L. M., Ponomarev E. A., Redmond G., Shaw N. J., and Uhlendorf I., Dynamic response of dye-sensitized nanocrystalline solar cells: characterization by intensity-modulated photocurrent spectroscopy, Journal of Physical Chemistry B. (1997) 101, no. 49, 10281–10289, 2-s2.0-0031553244.
Google Scholar
31 Eichberger R. and Willig F., Ultrafast electron injection from excited dye molecules into semiconductor electrodes, Chemical Physics. (1990) 141, no. 1, 159–173, 2-s2.0-2742521502.
Google Scholar
32 Tsai H. L., Tu C. S., and Su Y. J., Development of generalized photovoltaic model using MATLAB/SIMULINK, Proceedings of the World Congress on Engineering and Computer Science (WCECS ′08), October 2008, San Francisco, Calif, USA.
Google Scholar
33 Thongpron J., Kirtikara K., and Jivacate C., A method for the determination of dynamic resistance of photovoltaic modules under illumination, Solar Energy Materials and Solar Cells. (2006) 90, no. 18-19, 3078–3084, 2-s2.0-33748290037, https://doi.org/10.1016/j.solmat.2006.06.029.
Google Scholar
34 Yong V., Ho S. T., and Chang R. P., Modeling and simulation for dye-sensitized solar cells, Applied Physics Letters. 92, 3, 143506, https://doi.org/10.1063/1.2908204.
Google Scholar
35 Sze S. M., Physics of Semiconductor Devices, 1981, 2nd edition, Wiley, New York, NY, USA.
Google Scholar
36 Bose B. K., Szczesny P. M., and Steigerwald R. L., Microcomputer control of a residential photovoltaic power conditioning system, IEEE Transactions on Industry Applications. (1985) IA-21, no. 5, 1182–1191, 2-s2.0-0022231461.
Google Scholar
37 Zhou W., Yang H., and Fang Z., A novel model for photovoltaic array performance prediction, Applied Energy. (2007) 84, no. 12, 1187–1198, 2-s2.0-34548335144, https://doi.org/10.1016/j.apenergy.2007.04.006.
Web of Science® Google Scholar
38 Pysch D., Mette A., and Glunz S. W., A review and comparison of different methods to determine the series resistance of solar cells, Solar Energy Materials and Solar Cells. (2007) 91, no. 18, 1698–1706, 2-s2.0-34548247286, https://doi.org/10.1016/j.solmat.2007.05.026.
Google Scholar
39 Gratzel M., Solar energy conversion by dye-sensitized photovoltaic cells, Inorganic Chemistry. (2005) 44, no. 20, 6841–6851, https://doi.org/10.1021/ic0508371.
Google Scholar
40 Wang Q., Moser J., and Gratzel M., Electrochemical impedance spectroscopic analysis of dye-sensitized solar cells, The Journal of Physical Chemistry B. (2005) 109, no. 31, 14945–14953, https://doi.org/10.1021/jp052768h.
Web of Science® Google Scholar
41 Andrade L., Sousa J., Aguilar Ribeiro H., and Mendes A., Phenomenological modeling of dye-sensitized solar cells under transient conditions, Solar Energy. (2011) 85, no. 5, 781–793, 2-s2.0-79954592658, https://doi.org/10.1016/j.solener.2011.01.014.
Google Scholar
42 Koide N., Islam A., Chiba Y., and Han L., Improvement of efficiency of dye-sensitized solar cells based on analysis of equivalent circuit, Journal of Photochemistry and Photobiology A. (2006) 182, no. 3, 296–305, https://doi.org/10.1016/j.jphotochem.2006.04.030.
Google Scholar
43 Bisquert J., theory of the impedance of electron diffusion and recombination in a thin layer, The Journal of Physical Chemistry B. (2002) 106, no. 2, 325–333, https://doi.org/10.1021/jp011941g.
Google Scholar
44 Andrade L., Zakeeruddin S. M., Nazeeruddin M. K., Ribeiro H. A., Mendes A., and Gratzel M., Influence of sodium cations of N3 dye on the photovoltaic performance and stability of dye-sensitized solar cells, ChemPhysChem. (2009) 10, no. 7, 1117–1124, 2-s2.0-66449109122, https://doi.org/10.1002/cphc.200900111.
Web of Science® Google Scholar
45 Kern R., Sastrawan R., Ferber J., Stangl R., and Luther J., Modeling and interpretation of electrical impedance spectra of dye solar cells operated under open-circuit conditions, Electrochimica Acta. (2002) 47, no. 26, 4213–4225, 2-s2.0-0037048820, https://doi.org/10.1016/S0013-4686(02)00444-9.
10.1016/S0013-4686(02)00444-9
Web of Science® Google Scholar
46 Froment G. F. and Bischoff K. B., Chemical Reactor Analysis and Design, 1990, 2nd edition, John Wiley and Sons, New York, NY, USA.
Google Scholar
47 Hauch A. and Georg A., Diffusion in the electrolyte and charge-transfer reaction at the platinum electrode in dye-sensitized solar cells, Electrochimica Acta. (2001) 46, no. 22, 3457–3466, 2-s2.0-0035420922, https://doi.org/10.1016/S0013-4686(01)00540-0.
10.1016/S0013-4686(01)00540-0
Web of Science® Google Scholar
48 Mora-Seró I., Bisquert J., Fabregat-Santiago F., Garcia-Belmonte G., Zoppi G., Durose K., Proskuryakov Y., Oja I., Belaidi A., Dittrich T., Tena-Zaera R., Katty A., Lévy-Clément C., Barrioz V., and Irvine S. J. C., Implications of the negative capacitance observed at forward bias in nanocomposite and polycrystalline solar cells, Nano Letters. (2006) 6, no. 4, 640–650, 2-s2.0-33646386165, https://doi.org/10.1021/nl052295q.
Google Scholar
49 Gellings P. J. and Bouwmeester H. J., Handbook of Solid State Electrochemistry, 1997, CRC, Boca Raton, Fla, USA.
Google Scholar
50 Yadav P., Tripathi B., Lokhande M., and Kumar M., Estimation of steady state and dynamic parameters of low concentration photovoltaic system, Solar Energy Materials and Solar Cells. (2013) 112, 65–72, https://doi.org/10.1016/j.solmat.2013.01.012.
Google Scholar
51 Villanueva-Cab J., Oskam G., and Anta J. A., A simple numerical model for the charge transport and recombination properties of dye-sensitized solar cells: a comparison of transport-limited and transfer-limited recombination, Solar Energy Materials and Solar Cells. (2010) 94, no. 1, 45–50, 2-s2.0-70449526432, https://doi.org/10.1016/j.solmat.2009.06.004.
Google Scholar
52 Ocakoglu K., Yakuphanoglu F., Durrant J. R., and Icli S., The effect of temperature on the charge transport and transient absorption properties of K27 sensitized DSSC, Solar Energy Materials and Solar Cells. (2008) 92, no. 9, 1047–1053, 2-s2.0-45049088136, https://doi.org/10.1016/j.solmat.2008.03.006.
Google Scholar

Citing Literature

All articles

Effect of Varying Illumination and Temperature on Steady-State and Dynamic Parameters of Dye-Sensitized Solar Cell Using AC Impedance Modeling

Abstract

1. Introduction

2. Performance Prediction Model

2.1. Prediction of I-V Curve of DSSC

2.2. Prediction of Dynamic Resistance of DSSC

3. Validation and Analysis of Developed Model

3.1. Current-Voltage Characterization

3.2. Electrochemical Impedance Spectroscopy

4. Results and Discussion

4.1. Effect of Illumination on Steady and Dynamic Parameters

4.2. Effect of DSSC’s Working Temperature on Steady and Dynamic Parameters

5. Conclusions

Acknowledgment

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Effect of Varying Illumination and Temperature on Steady-State and Dynamic Parameters of Dye-Sensitized Solar Cell Using AC Impedance Modeling

Abstract

1. Introduction

2. Performance Prediction Model

2.1. Prediction of I-V Curve of DSSC

2.2. Prediction of Dynamic Resistance of DSSC

3. Validation and Analysis of Developed Model

3.1. Current-Voltage Characterization

3.2. Electrochemical Impedance Spectroscopy

4. Results and Discussion

4.1. Effect of Illumination on Steady and Dynamic Parameters

4.2. Effect of DSSC’s Working Temperature on Steady and Dynamic Parameters

5. Conclusions

Acknowledgment

References

Citing Literature

Figures

References

Related

Information