Volume 2013, Issue 1 645262

Research Article

Open Access

Exponential Stability and Periodicity of Fuzzy Delayed Reaction-Diffusion Cellular Neural Networks with Impulsive Effect

Guowei Yang,

Guowei Yang

College of Information Engineering, Nanchang Hangkong University, Nanchang 330063, China nchu.edu.cn

Search for more papers by this author

Yonggui Kao,

Yonggui Kao

Space Control and Inertial Technology Research Center, Harbin Institute of Technology, Harbin, Heilongjiang 150001, China hit.edu.cn

Search for more papers by this author

Changhong Wang,

Corresponding Author

Changhong Wang

[email protected]

Space Control and Inertial Technology Research Center, Harbin Institute of Technology, Harbin, Heilongjiang 150001, China hit.edu.cn

Search for more papers by this author

Guowei Yang,

Guowei Yang

College of Information Engineering, Nanchang Hangkong University, Nanchang 330063, China nchu.edu.cn

Search for more papers by this author

Yonggui Kao,

Yonggui Kao

Space Control and Inertial Technology Research Center, Harbin Institute of Technology, Harbin, Heilongjiang 150001, China hit.edu.cn

Search for more papers by this author

Changhong Wang,

Corresponding Author

Changhong Wang

[email protected]

Space Control and Inertial Technology Research Center, Harbin Institute of Technology, Harbin, Heilongjiang 150001, China hit.edu.cn

Search for more papers by this author

First published: 20 March 2013

https://doi.org/10.1155/2013/645262

Citations: 4

Academic Editor: Tingwen Huang

Share a link

Email
Wechat
Bluesky

Abstract

This paper considers dynamical behaviors of a class of fuzzy impulsive reaction-diffusion delayed cellular neural networks (FIRDDCNNs) with time-varying periodic self-inhibitions, interconnection weights, and inputs. By using delay differential inequality, M-matrix theory, and analytic methods, some new sufficient conditions ensuring global exponential stability of the periodic FIRDDCNN model with Neumann boundary conditions are established, and the exponential convergence rate index is estimated. The differentiability of the time-varying delays is not needed. An example is presented to demonstrate the efficiency and effectiveness of the obtained results.

1. Introduction

The fuzzy cellular neural networks (FCNNs) model, which combines fuzzy logic with the structure of traditional neural networks (CNNs) [1–3], has been proposed by Yang et al. [4, 5]. Unlike previous CNNs structures, the FCNNs model has fuzzy logic between its template and input and/or output besides the “sum of product” operation. Studies have shown that the FCNNs model is a very useful paradigm for image processing and pattern recognition [6–8]. These applications heavily depend on not only the dynamical analysis of equilibrium points but also on that of the periodic oscillatory solutions. In fact, the human brain is naturally in periodic oscillatory [9], and the dynamical analysis of periodic oscillatory solutions is very important in learning theory [10, 11], because learning usually requires repetition. Moreover, an equilibrium point can be viewed as a special periodic solution of neural networks with arbitrary period. Stability analysis problems for FCNNs with and without delays have recently been probed; see [12–22] and the references therein. Yuan et al. [13] have investigated stability of FCNNs by linear matrix inequality approach, and several criteria have been provided for checking the periodic solutions for FCNNs with time-varying delays. Huang [14] has probed exponential stability of fuzzy cellular neural networks with distributed delay, without considering reaction-diffusion effects.

Strictly speaking, reaction-diffusion effects cannot be neglected in both biological and man-made neural networks [19–32], especially when electrons are moving in noneven electromagnetic field. In [19], stability is considered for FCNNs with diffusion terms and time-varying delay. Wang and Lu [20] have probed global exponential stability of FCNNs with delays and reaction-diffusion terms. Song and Wang [21] have studied dynamical behaviors of fuzzy reaction-diffusion periodic cellular neural networks with variable coefficients and delays without considering pulsing effects. Wang et al. [22] have discussed exponential stability of impulsive stochastic fuzzy reaction-diffusion Cohen-Grossberg neural networks with mixed delays. Zhao and Mao [30] have investigated boundedness and stability of nonautonomous cellular neural networks with reaction-diffusion terms. Zhao and Wang [31] have considered existence of periodic oscillatory solution of reaction-diffusion neural networks with delays without fuzzy logic and impulsive effect.

As we all know, many practical systems in physics, biology, engineering, and information science undergo abrupt changes at certain moments of time because of impulsive inputs [33]. Impulsive differential equations and impulsive neural networks have been received much interest in recent years; see, for example, [34–42] and the references therein. Yang and Xu [36] have investigated existence and exponential stability of periodic solution for impulsive delay differential equations and applications. Li and Lu [38] have discussed global exponential stability and existence of periodic solution of Hopfield-type neural networks with impulses without reaction-diffusion. To the best of our knowledge, few authors have probed the existence and exponential stability of the periodic solutions for the FIRDDCNN model with variable coefficients, and time-varying delays. As a result of the simultaneous presence of fuzziness, pulsing effects, reaction-diffusion phenomena, periodicity, variable coefficients and delays, the dynamical behaviors of this kind of model become much more complex and have not been properly addressed, which still remain important and challenging.

Motivated by the above discussion, we will establish some sufficient conditions for the existence and exponential stability of periodic solutions of this kind of FIRDDCNN model, applying delay differential inequality, M-matrix theory, and analytic methods. An example is employed to demonstrate the usefulness of the obtained results.

Notations. Throughout this paper, ℝⁿ and ℝ^n×m denote, respectively, the n-dimensional Euclidean space and the set of all n × m real matrices. The superscript “T” denotes matrix transposition and the notation X ≥ Y (resp., X > Y), where X and Y are symmetric matrices, means that X − Y is positive semidefinite (resp., positive definite). Ω = {x = (x₁, …, x_m) ^T, |x_i | < μ} is a bounded compact set in space ℝ^m with smooth boundary ∂Ω and measure mes Ω > 0; Neumann boundary condition ∂u_i/∂n = 0 is the outer normal to ∂Ω; L²(Ω) is the space of real functions Ω which are L² for the Lebesgue measure. It is a Banach space with the norm , where u(t, x) = (u₁(t, x), …,u_n(t, x)) ^T, ∥u_i(t, x)∥₂ = (∫_Ω | u_i(t, x)|²dx) ^1/2, |u(t, x)| = (|u₁(t, x)|, …, |u_n(t, x) | ) ^T. For function g(x) with positive period ω, we denote . Sometimes, the arguments of a function or a matrix will be omitted in the analysis when no confusion can arise.

2. Preliminaries

Consider the impulsive fuzzy reaction-diffusion delayed cellular neural networks (FIRDDCNN) model:

()

where n ≥ 2 is the number of neurons in the network and u_i(t, x) corresponds to the state of the ith neuron at time t and in space x; D = diag (D₁, D₂, …, D_n) is the diffusion-matrix and D_i ≥ 0;

is the Laplace operator; f_j(u_j(t, x)) denotes the activation function of the jth unit and v_j(t) the activation function of the jth unit; J_i(t) is an input at time t; c_i(t) > 0 represents the rate with which the ith unit will reset its potential to the resting state in isolation when disconnected from the networks and external inputs at time t; a_ij(t) and b_ij(t) are elements of feedback template and feed forward template at time t, respectively. Moreover, in model (1), α_ij(t), β_ij(t), T_ij(t), and H_ij(t) are elements of fuzzy feedback MIN template, fuzzy feedback MAX template, fuzzy feed forward MIN template, and fuzzy feed forward MAX template at time t, respectively; the symbols “⋀" and “⋁" denote the fuzzy AND and fuzzy OR operation, respectively; time-varying delay τ_j(t) is the transmission delay along the axon of the jth unit and satisfies 0 ≤ τ_j(t) ≤ τ_j (τ_j is a constant); the initial condition ϕ_i(s, x) is bounded and continuous on [−τ, 0] × Ω, where τ = max _1≤j≤nτ_j. The fixed moments t_k satisfy 0 = t₀ < t₁ < t₂ … , lim _k→+∞t_k = +∞, k ∈ ℕ.

and

denote the right-hand and left-hand limits at t_k, respectively. We always assume

, for all k ∈ N. The initial value functions ψ(s, x) belong to PC_Ω([−τ, 0] × Ω; Rⁿ). PC_Ω(J × Ω, L²(Ω)) = {ψ : J × Ω → L²(Ω)∣ for every t ∈ J, ψ(t, x) ∈ L²(Ω); for any fixed x ∈ Ω, ψ(t, x) is continuous for all but at most countable points s ∈ J and at these points, ψ(s⁺, x) and ψ(s⁻, x) exist, ψ(s⁺, x) = ψ(s⁻, x)}, where ψ(s⁺, x) and ψ(s⁻, x) denote the right-hand and left-hand limit of the function ψ(s, x), respectively. Especially, let PC_Ω = PC([−τ, 0] × Ω, L²(Ω)). For any ψ(t, x) = (ψ₁(t, x), …, ψ_n(t, x)) ∈ PC_Ω, suppose that |ψ_i(t, x)|_τ = sup _−τ<s≤0 | ψ_i(t + s, x)| exists as a finite number and introduce the norm

, where ∥ψ_i(t)∥₂ = (∫_Ω | ψ_i(t, x)|²dx) ^1/2.

Throughout the paper, we make the following assumptions.

(H1) There exists a positive diagonal matrix F = diag (F₁, F₂, …, F_n), and G = diag (G₁, G₂, …, G_n) such that
()
for all x ≠ y, j = 1,2, …, n.
(H2) c_i(t) > 0, a_ij(t), b_ij(t), α_ij(t), β_ij(t), T_ij(t), H_ij(t), v_i(t), I_i(t), and τ_j(t) ≥ 0 are periodic function with a common positive period ω for all t ≥ t₀, i, j = 1,2, …, n.
(H3) For ω > 0, i = 1,2, …, n, there exists q ∈ Z₊ such that t_k + ω = t_k+q, I_ik(u_i) = I_i(k+q)(u_i) and I_ik(u_i(t_k, x)) are Lipschitz continuous in ℝⁿ.

Definition 1. The model in (1) is said to be globally exponentially periodic if (i) there exists one ω-periodic solution and (ii) all other solutions of the model converge exponentially to it as t → +∞.

Definition 2 (see [26].)Let C = ([t − τ, t], ℝⁿ), where τ ≥ 0 and F(t, x, y) ∈ C(ℝ⁺ × ℝⁿ × C, ℝⁿ). Then the function F(t, x, y) = (f₁(t, x, y), f₂(t, x, y), …, f_n(t, x, y)) ^T is called an M-function, if (i) for every t ∈ ℝ⁺, x ∈ ℝⁿ, y⁽¹⁾ ∈ C, there holds F(t, x, y⁽¹⁾) ≤ F(t, x, y⁽²⁾), for y⁽¹⁾ ≤ y⁽²⁾, where and ; (ii) every ith element of F satisfies f_i(t, x⁽¹⁾, y) ≤ f_i(t, x⁽²⁾, y) for any y ∈ C, t ≥ t₀, where arbitrary x⁽¹⁾ and x⁽²⁾ (x⁽¹⁾ ≤ x⁽²⁾) belong to ℝⁿ and have the same ith component . Here, .

Definition 3 (see [26].)A real matrix A = (a_ij) _n×n is said to be a nonsingular M-matrix if a_ij ≤ 0 (i ≠ j; i, j = 1, …, n) and all successive principal minors of A are positive.

Lemma 4 (see [13].)Let u and u^* be two states of the model in (1), then we have

()

Lemma 5 (see [26].)Assume that F(t, x, y) is an M-function, and (i) x(t) < y(t), t ∈ [t − τ, t₀], (ii) D⁺y(t) > F(t, y(t), y^s(t)), D⁺x(t) ≤ F(t, x(t), x^s(t)), t ≥ t₀, where x^s(t) = sup _{−τ≤s≤0}x(t + s), y^s(t) = sup _{−τ≤s≤0}y(t + s). Then x(t) < y(t), t ≥ t₀.

3. Main Results and Proofs

We should first point out that, under assumptions (H1), (H2), and (H3), the FIRDDCNN model (1) has at least one ω-periodic solution of [26]. The proof of the existence of the ω-periodic solution of (1) can be carried out similar to [26, 28] by the nonlinear functional analysis methods such as topological degree and here is omitted. We will mainly discuss the uniqueness of the periodic solution and its exponential stability.

Theorem 6. Assume that (H1)–(H3) holds. Furthermore, assume that the following conditions hold

(H4) is a nonsingular M-matrix.
(H5) The impulsive operators h_k(u) = u + I_k(u) is Lipschitz continuous in ℝⁿ; that is, there exists a nonnegative diagnose matrix Γ_k = diag (γ_1k, …, γ_nk) such that |h_k(u) − h_k(u^*)| ≤ Γ_k | u − u^*| for all u, u^* ∈ ℝⁿ, k ∈ N⁺, where |h_k(u)| = (|h_1k(u₁)|, …, |h_nk(u_n) | ) ^T, I_k(u) = (I_1k(u₁), …,I_nk(u_n)) ^T.
(H6) , where η_k = max _1≤i≤n {1, γ_ik}, k ∈ N⁺.

Then the model (1) is global exponential periodic and the exponential convergence rate index λ − η and λ can be estimated by

()

where

and ξ_i > 0,

, satisfies

Proof. For any ϕ, ψ ∈ PC_Ω, let u(t, x, ϕ) = (u₁(t, x, ϕ), …, u_n(t, x, ϕ)) ^T be a periodic solution of the system (1) starting from ϕ and u(t, x, ψ) = (u₁(t, x, ψ), …, u_n(t, x, ψ)) ^T, a solution of the system (1) starting from ψ. Define

()

and we can see that u_t(ϕ, x), u_t(ψ, x) ∈ PC_Ω for all t > 0. Let U_i = u_i(t, x, ϕ) − u_i(t, x, ψ), then from (1) we get

()

for all t ≠ t_k, x ∈ Ω, i = 1, …, n.

Multiplying both sides of (6) by U_i and integrating it in Ω, we have

()

for t ≠ t_k, x ∈ Ω, i = 1, …, n. By boundary condition and Green Formula, we can get

()

Then, from (8), (9), (H1)-(H2), Lemma 4, and the Holder inequality,

()

Thus,

()

for i = 1, …, n. Since

is a nonsingular M-matrix, there exists a vector ξ = (ξ₁, …, ξ_n) ^T > 0 such that

()

Considering functions

()

we know from (11) that Ψ_i(0) < 0 and Ψ_i(y) is continuous. Since dΨ_i(y)/dy > 0, Ψ_i(y) is strictly monotonically increasing, there exists a scalar λ_i > 0 such that

()

Choosing 0 < λ < min {λ₁, …, λ_n}, we have

()

That is,

()

Furthermore, choose a positive scalar p large enough such that

()

For any ε > 0, let

()

From (15)–(17), we obtain

()

where

and

. It is easy to verify that V(t, r(t), r^s(t)) is an M-function. It follows also from (16) and (17) that

()

Denote

()

where

, then

()

From (10), we can obtain

()

Now, it follows from (18)–(22) and Lemma 5 that

()

Letting ε → 0, we have

()

And moreover, from (24), we get

()

Let

, then

. Define W(t) = ∥u_t(x, ϕ) − u_t(x, ψ)∥₂; it follows from (25) and the definitions of u_t(ϕ, x) and u_t(ψ, x) that

()

It is easily observed that

()

Because (26) holds, we can suppose that for l ≤ k inequality

()

holds, where η₀ = 1. When l = k + 1, we note (H5) that

()

where

is the spectral radius of

. Let

, by (28), (29), and η ≥ 1, we obtain

()

Combining (10), (17), (30), and Lemma 5, we get

()

Applying mathematical induction, we conclude that

()

From (H6) and (32), we have

()

This means that

()

choosing a positive integer N such that

()

Define a Poincare mapping 𝔇 : Γ → Γ by

()

Then

()

Setting t = Nω in (34), from (35) and (37), we have

()

which implies that 𝔇^N is a contraction mapping. Thus, there exists a unique fixed point ϕ^* ∈ Γ such that

()

From (37), we know that 𝔇(ϕ^*) is also a fixed point of 𝔇^N, and then it follows from the uniqueness of the fixed point that

()

Let u(t, x, ϕ^*) be a solution of the model (1), then u(t + ω, x, ϕ^*) is also a solution of the model (1). Obviously,

()

for all t ≥ t₀. Hence, u(t + ω, x, ϕ^*) = u(t, x, ϕ^*), which shows that u(t, x, ϕ^*) is exactly one ω-periodic solution of model (1). It is easy to see that all other solutions of model (1) converge to this periodic solution exponentially as t → +∞, and the exponential convergence rate index is λ − η. The proof is completed.

Remark 7. When c_i(t) = c_i, a_ij(t) = a_ij, b_ij(t) = b_ij, α_ij(t) = α_ij, β_ij(t) = β_ij, T_ij(t) = T_ij, H_ij(t) = H_ij, v_i(t) = v_i, I_i(t) = I_i, and τ_t = τ_i(c_i, a_ij, b_ij, α_ij, β_ij, T_ij, H_ij, v_i, I_i, and τ_i are constants), then the model (1) is changed into

()

For any positive constant ω ≥ 0, we have c_i(t + ω) = c_i(t), a_ij(t + ω) = a_ij(t), b_ij(t + ω) = b_ij(t), α_ij(t + ω) = α_ij(t), β_ij(t + ω) = β_ij(t), T_ij(t + ω) = T_ij(t), H_ij(t + ω) = H_ij(t), v_i(t + ω) = v_i(t), I_i(t + ω) = I_i(t), and τ_i(t + ω) = τ_i(t) for t ≥ t₀. Thus, the sufficient conditions in Theorem 6 are satisfied.

Remark 8. If I_k(·) = 0, the model (1) is changed into

()

which has been discussed in [22]. As Song and Wang have pointed out, the model (43) is more general than some well-studied fuzzy neural networks. For example, when c_i(t) > 0, a_ij(t), b_ij(t), α_ij(t), β_ij(t), T_ij(t), H_ij(t), v_i(t), and I_i(t) are all constants, the model in (43) reduces the model which has been studied by Huang [19]. Moreover, if D_i = 0, τ_i(t) = 0, f_i(θ) = g_i(θ) = (1/2)(|θ + 1 | −|θ − 1|), (i = 1, …, n), then model (42) covers the model studied by Yang et al. [4, 5] as a special case. If D_i = 0 and τ_j(t) is assumed to be differentiable for i, j = 1,2, …, n, then model (43) can be specialized to the model investigated in Liu and Tang [12] and Yuan et al. [13]. Obviously, our results are less conservative than that of the above-mentioned literature, because they do not consider impulsive effects.

4. Numerical Examples

Example 9. Consider a two-neuron FIRDDCNN model:

()

where i = 1,2. c₁(t) = 26, c₂(t) = 20.8, a₁₁(t) = −1 − cos (t), a₁₂(t) = 1 + cos (t), a₂₁(t) = 1 + sin(t), a₂₂(t) = −1 − sin(t), D₁ = 8, D₂ = 4, ∂u_i(t, x)/∂n = 0 (t ≥ t₀, x = 0,2π), γ_1k = 0.4, γ_2k = 0.2, ψ₁(·) = ψ₁(·) = 5, b₁₁(t) = b₂₁(t) = cos (t), b₁₂(t) = b₂₂(t) = −cos (t), J₁(t) = J₂(t) = 1, H₁₁(t) = H₂₁(t) = sin(t), H₁₂(t) = H₂₂(t) = −1 + sin(t), T₁₁(t) = T₂₁(t) = −sin(t), T₁₂(t) = T₂₂(t) = 2 + sin(t), τ₁(t) = τ₂(t) = 1, f_j(u_j) = u_j(t, x) (j = 1,2),

, α₁₁(t) = −12.8, α₂₁(t) = α₁₂(t) = −1 + cos (t), α₂₂(t) = −10, β₁₁(t) = 12.8, β₁₂(t) = −1 + sin(t) = β₂₁(t), β₂₂(t) = 10, v_j(t) = sin(t). We assume that there exists q = 6 such that t_k + 2π = t_k+q. Obviously, f₁, f₂, g₁, and g₂ satisfy the assumption (H1) with F₁ = F₂ = G₁ = G₂ = 1 and (H2) and (H3) are satisfied with a common positive period 2π

()

is a nonsingular M-matrix. The conditions of Theorem 6 are satisfied, hence there exists exactly one 2ω-periodic solution of the model and all other solutions of the model converge exponentially to it as t → +∞. Furthermore, the exponential converging index can be calculated as λ = 0.021, because here η_k = 1 and η = 0. The simulation results are shown in Figures 1, 2, 3, and 4, respectively.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

State response u1(t, x) of model (44) without impulsive effects.

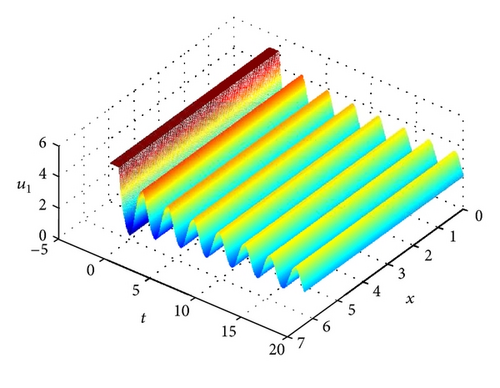
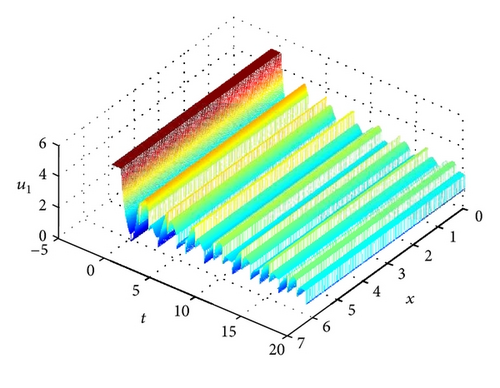
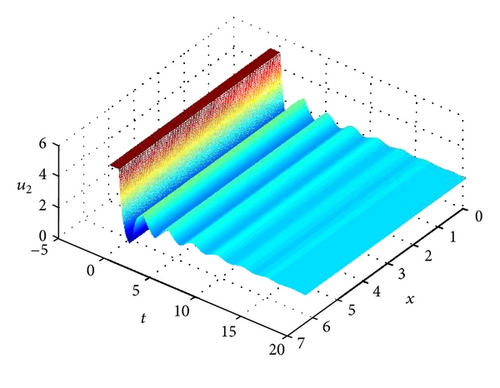
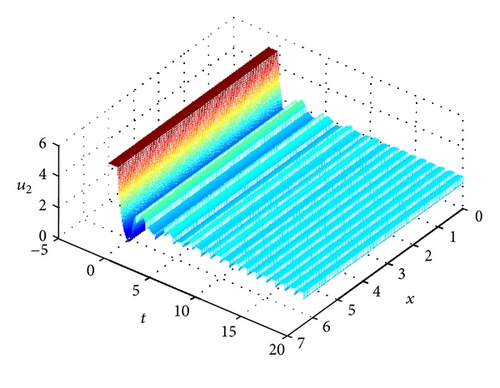
5. Conclusions

In this paper, periodicity and global exponential stability of a class of FIRDDCNN model with variable both coefficients and delays have been investigated. By using Halanay’s delay differential inequality, M-matrix theory, and analytic methods, some new sufficient conditions have been established to guarantee the existence, uniqueness, and global exponential stability of the periodic solution. Moreover, the exponential convergence rate index can be estimated. An example and its simulation have been given to show the effectiveness of the obtained results. In particular, the differentiability of the time-varying delays has been removed. The dynamic behaviors of fuzzy neural networks with the property of exponential periodicity are of great importance in many areas such as learning systems.

Acknowledgments

The authors would like to thank the editors and the anonymous reviewers for their valuable comments and constructive suggestions. This research is supported by the Natural Science Foundation of Guangxi Autonomous Region (no. 2012GXNSFBA053003), the National Natural Science Foundations of China (60973048, 61272077, 60974025, 60673101, and 60939003), National 863 Plan Project (2008 AA04Z401, 2009 AA043404), the Natural Science Foundation of Shandong Province (no. Y2007G30), the Scientific and Technological Project of Shandong Province (no. 2007GG3WZ04016), the Science Foundation of Harbin Institute of Technology (Weihai) (HIT (WH) 200807), the Natural Scientific Research Innovation Foundation in Harbin Institute of Technology (HIT. NSRIF. 2001120), the China Postdoctoral Science Foundation (2010048 1000), and the Shandong Provincial Key Laboratory of Industrial Control Technique (Qingdao University).

References

1 Chua L. O. and Yang L., Cellular neural networks: theory, IEEE Transactions on Circuits and Systems. (1988) 35, no. 10, 1257–1272, https://doi.org/10.1109/31.7600, MR960777, ZBL0663.94022.
10.1109/31.7600
Web of Science® Google Scholar
2 Chua L. O. and Yang L., Cellular neural networks: applications, IEEE Transactions on Circuits and Systems. (1988) 35, no. 10, 1273–1290, https://doi.org/10.1109/31.7601, MR960778.
10.1109/31.7601
Web of Science® Google Scholar
3 Roska T. and Chua L. O., Cellular neural networks with non-linear and delay-type template elements and non-uniform grids, International Journal of Circuit Theory and Applications. (1992) 20, no. 5, 469–481, 2-s2.0-0026913847.
10.1002/cta.4490200504
Web of Science® Google Scholar
4 Yang T., Yang L. B., Wu C. W., and Chua L. O., Fuzzy cellular neural networks: theory, Proceedings of the 4th IEEE International Workshop on Cellular Neural Networks, and Their Applications (CNNA ′96), June 1996, 181–186, 2-s2.0-0030409908.
Google Scholar
5 Yang T. and Yang L.-B., The global stability of fuzzy cellular neural network, IEEE Transactions on Circuits and Systems I. (1996) 43, no. 10, 880–883, https://doi.org/10.1109/81.538999, MR1416906.
10.1109/81.538999
Web of Science® Google Scholar
6 Yang T., Yang L. B., Wu C. W., and Chua L. O., Fuzzy cellular neural networks: applications, Proceedings of the 4th IEEE International Workshop on Cellular Neural Networks, and Their Applications (CNNA ′96), June 1996, 225–230, 2-s2.0-0030379550.
Google Scholar
7 Wang S. T., Chung K. F. L., and Duan F., Applying the improved fuzzy cellular neural network IFCNN to white blood cell detection, Neurocomputing. (2007) 70, no. 7–9, 1348–1359, 2-s2.0-33847360582, https://doi.org/10.1016/j.neucom.2006.07.012.
10.1016/j.neucom.2006.07.012
Web of Science® Google Scholar
8 Barbounis T. G. and Theocharis J. B., A locally recurrent fuzzy neural network with application to the wind speed prediction using spatial correlation, Neurocomputing. (2007) 70, no. 7–9, 1525–1542, 2-s2.0-33847369874, https://doi.org/10.1016/j.neucom.2006.01.032.
10.1016/j.neucom.2006.01.032
Web of Science® Google Scholar
9 Zhao H., Global exponential stability and periodicity of cellular neural networks with variable delays, Physics Letters A. (2005) 336, no. 4-5, 331–341, 2-s2.0-13844264516, https://doi.org/10.1016/j.physleta.2004.12.001.
10.1016/j.physleta.2004.12.001
CAS Web of Science® Google Scholar
10 Townley S., Ilchmann A., Weiss M. G., Mcclements W., Ruiz A. C., Owens D. H., and Pratzel-Wolters D., Existence and learning of oscillations in recurrent neural networks, IEEE Transactions on Neural Networks. (2000) 11, no. 1, 205–214, 2-s2.0-0033640658, https://doi.org/10.1109/72.822523.
10.1109/72.822523
CAS PubMed Web of Science® Google Scholar
11 Huang Z. and Xia Y., Exponential periodic attractor of impulsive BAM networks with finite distributed delays, Chaos, Solitons & Fractals. (2009) 39, no. 1, 373–384, https://doi.org/10.1016/j.chaos.2007.04.014, MR2504572, ZBL1197.34124.
10.1016/j.chaos.2007.04.014
Web of Science® Google Scholar
12 Liu Y. and Tang W., Exponential stability of fuzzy cellular neural networks with constant and time-varying delays, Physics Letters A. (2004) 323, no. 3-4, 224–233, https://doi.org/10.1016/j.physleta.2004.01.064, MR2050486, ZBL1118.81400.
10.1016/j.physleta.2004.01.064
CAS Web of Science® Google Scholar
13 Yuan K., Cao J., and Deng J., Exponential stability and periodic solutions of fuzzy cellular neural networks with time-varying delays, Neurocomputing. (2006) 69, no. 13–15, 1619–1627, 2-s2.0-33745209223, https://doi.org/10.1016/j.neucom.2005.05.011.
10.1016/j.neucom.2005.05.011
Web of Science® Google Scholar
14 Huang T., Exponential stability of fuzzy cellular neural networks with distributed delay, Physics Letters A. (2006) 351, no. 1-2, 48–52, 2-s2.0-31744447713, https://doi.org/10.1016/j.jviromet.2005.11.016.
10.1016/j.physleta.2005.10.060
CAS Web of Science® Google Scholar
15 Bao G., Wen S., and Zeng Z., Robust stability analysis of interval fuzzy Cohen-Grossberg neural networks with piecewise constant argument of generalized type, Neural Networks. (2012) 33, 32–41.
10.1016/j.neunet.2012.04.003
PubMed Web of Science® Google Scholar
16 Zhao H., Ding N., and Chen L., Almost sure exponential stability of stochastic fuzzy cellular neural networks with delays, Chaos, Solitons & Fractals. (2009) 40, no. 4, 1653–1659, https://doi.org/10.1016/j.chaos.2007.09.044, MR2531255, ZBL1198.34173.
10.1016/j.chaos.2007.09.044
Web of Science® Google Scholar
17 Ding W., Han M., and Li M., Exponential lag synchronization of delayed fuzzy cellular neural networks with impulses, Physics Letters A. (2009) 373, no. 8-9, 832–837, https://doi.org/10.1016/j.physleta.2008.12.049, MR2498598, ZBL1228.34075.
10.1016/j.physleta.2008.12.049
CAS Web of Science® Google Scholar
18 Chen L. and Zhao H., Stability analysis of stochastic fuzzy cellular neural networks with delays, Neurocomputing. (2008) 72, no. 1–3, 436–444, 2-s2.0-55949088751, https://doi.org/10.1016/j.neucom.2007.12.005.
10.1016/j.neucom.2007.12.005
Web of Science® Google Scholar
19 Huang T., Exponential stability of delayed fuzzy cellular neural networks with diffusion, Chaos, Solitons & Fractals. (2007) 31, no. 3, 658–664, https://doi.org/10.1016/j.chaos.2005.10.015, MR2262300, ZBL1138.35414.
10.1016/j.chaos.2005.10.015
Web of Science® Google Scholar
20 Wang J. and Lu J. G., Global exponential stability of fuzzy cellular neural networks with delays and reaction-diffusion terms, Chaos, Solitons & Fractals. (2008) 38, no. 3, 878–885, https://doi.org/10.1016/j.chaos.2007.01.032, MR2423369, ZBL1146.35315.
10.1016/j.chaos.2007.01.032
Web of Science® Google Scholar
21 Song Q. and Wang Z., Dynamical behaviors of fuzzy reaction-diffusion periodic cellular neural networks with variable coefficients and delays, Applied Mathematical Modelling. (2009) 33, no. 9, 3533–3545, https://doi.org/10.1016/j.apm.2008.11.017, MR2519112, ZBL1185.35129.
10.1016/j.apm.2008.11.017
Web of Science® Google Scholar
22 Wang C., kao Y., and Yang G., Exponential stability of impulsive stochastic fuzzy reaction-diffusion Cohen-Grossberg neural networks with mixed delays, Neurocomputing. (2012) 89, 55–63.
10.1016/j.neucom.2012.01.022
Web of Science® Google Scholar
23 Serrano-Gotarredona T. and Linares-Barranco B., Log-Domain Implementation of Complex Dynamics Reaction-Diffusion Neural Networks, IEEE Transactions on Neural Networks. (2003) 14, no. 5, 1337–1355, 2-s2.0-0242443314, https://doi.org/10.1109/TNN.2003.816374.
10.1109/TNN.2003.816374
CAS PubMed Google Scholar
24 Liang J. and Cao J., Global exponential stability of reaction-diffusion recurrent neural networks with time-varying delays, Physics Letters A. (2003) 314, no. 5-6, 434–442, 2-s2.0-0041661956, https://doi.org/10.1016/S0375-9601(03)00945-9.
10.1016/S0375-9601(03)00945-9
CAS Web of Science® Google Scholar
25 Wang L. and Xu D., Asymptotic behavior of a class of reaction-diffusion equations with delays, Journal of Mathematical Analysis and Applications. (2003) 281, no. 2, 439–453, https://doi.org/10.1016/S0022-247X(03)00112-4, MR1982665, ZBL1031.35065.
10.1016/S0022-247X(03)00112-4
Web of Science® Google Scholar
26 Wang L. and Xu D., Global exponential stability of Hopfield reaction-diffusion neural networks with time-varying delays, Science in China. Series F. (2003) 46, no. 6, 466–474, https://doi.org/10.1360/02yf0146, MR2042159, ZBL1186.82062.
10.1360/02yf0146
Web of Science® Google Scholar
27 Yang Z. and Xu D., Global dynamics for non-autonomous reaction-diffusion neural networks with time-varying delays, Theoretical Computer Science. (2008) 403, no. 1, 3–10, https://doi.org/10.1016/j.tcs.2008.04.044, MR2435627, ZBL1155.68076.
10.1016/j.tcs.2008.04.044
Web of Science® Google Scholar
28 Kao Y. G., Gao C. C., and Wang D. K., Global exponential stability of reaction-diffusion Hopfield neural networks with continuously distributed delays, Mathematica Applicata. (2008) 21, no. 3, 457–462, MR2455139, ZBL1174.92306.
Google Scholar
29 Kao Y.-G., Guo J.-F., Wang C.-H., and Sun X.-Q., Delay-dependent robust exponential stability of Markovian jumping reaction-diffusion Cohen-Grossberg neural networks with mixed delays, Journal of the Franklin Institute. (2012) 349, no. 6, 1972–1988, https://doi.org/10.1016/j.jfranklin.2012.04.005, MR2935271.
10.1016/j.jfranklin.2012.04.005
Web of Science® Google Scholar
30 Zhao H. and Mao Z., Boundedness and stability of nonautonomous cellular neural networks with reaction-diffusion terms, Mathematics and Computers in Simulation. (2009) 79, no. 5, 1603–1617, https://doi.org/10.1016/j.matcom.2008.07.008, MR2488108, ZBL1171.35326.
10.1016/j.matcom.2008.07.008
Web of Science® Google Scholar
31 Zhao H. and Wang G., Existence of periodic oscillatory solution of reaction-diffusion neural networks with delays, Physics Letters A. (2005) 343, no. 5, 372–383, https://doi.org/10.1016/j.physleta.2005.05.098, MR2152026, ZBL1194.35221.
10.1016/j.physleta.2005.05.098
CAS Web of Science® Google Scholar
32 Gan Q., Exponential synchronization of stochastic Cohen-Grossberg neural networks with mixed time-varying delays and reaction-diffusion via periodically intermittent control, Neural Networks. (2012) 31, 12–21.
10.1016/j.neunet.2012.02.039
PubMed Web of Science® Google Scholar
33 Lakshmikantham V., Baĭnov D. D., and Simeonov P. S., Theory of Impulsive Differential Equations, 1989, 6, World Scientific, Teaneck, NJ, USA, Series in Modern Applied Mathematics, MR1082551.
10.1142/0906
Google Scholar
34 Bainov D. D. and Simeonov P. S., Impulsive Differential Equations: Periodic Solutions and Applications, 1993, Longman, Harlow, UK.
Google Scholar
35 Song X., Xin X., and Huang W., Exponential stability of delayed and impulsive cellular neural networks with partially Lipschitz continuous activation functions, Neural Networks. (2012) 29-30, 80–90.
10.1016/j.neunet.2012.01.006
PubMed Web of Science® Google Scholar
36 Yang Z. and Xu D., Existence and exponential stability of periodic solution for impulsive delay differential equations and applications, Nonlinear Analysis: Theory, Methods & Applications. (2006) 64, no. 1, 130–145, https://doi.org/10.1016/j.na.2005.06.014, MR2183833, ZBL1092.34034.
10.1016/j.na.2005.06.014
Web of Science® Google Scholar
37 Yang X., Liao X., Evans D. J., and Tang Y., Existence and stability of periodic solution in impulsive Hopfield neural networks with finite distributed delays, Physics Letters A. (2005) 343, no. 1–3, 108–116, 2-s2.0-21744433519, https://doi.org/10.1016/j.physleta.2005.06.008.
10.1016/j.physleta.2005.06.008
CAS Web of Science® Google Scholar
38 Li Y. and Lu L., Global exponential stability and existence of periodic solution of Hopfield-type neural networks with impulses, Physics Letters A. (2004) 333, no. 1-2, 62–71, https://doi.org/10.1016/j.physleta.2004.09.083, MR2101962, ZBL1123.34303.
10.1016/j.physleta.2004.09.083
CAS Web of Science® Google Scholar
39 Li Y., Zhu L., and Liu P., Existence and stability of periodic solutions of delayed cellular neural networks, Nonlinear Analysis: Real World Applications. (2006) 7, no. 2, 225–234, https://doi.org/10.1016/j.nonrwa.2005.02.004, MR2192599, ZBL1086.92002.
10.1016/j.nonrwa.2005.02.004
Web of Science® Google Scholar
40 Guan Z. H. and Chen G., On delayed impulsive Hopfield neural networks, Neural Networks. (1999) 12, no. 2, 273–280, 2-s2.0-0033104380, https://doi.org/10.1016/S0893-6080(98)00133-6.
10.1016/S0893-6080(98)00133-6
PubMed Web of Science® Google Scholar
41 Guan Z. H., Lam J., and Chen G., On impulsive autoassociative neural networks, Neural Networks. (2000) 13, no. 1, 63–69, 2-s2.0-0033967086, https://doi.org/10.1016/S0893-6080(99)00095-7.
10.1016/S0893-6080(99)00095-7
CAS PubMed Web of Science® Google Scholar
42 Ding W., Synchronization of delayed fuzzy cellular neural networks with impulsive effects, Communications in Nonlinear Science and Numerical Simulation. (2009) 14, no. 11, 3945–3952, https://doi.org/10.1016/j.cnsns.2009.02.013, MR2522897, ZBL1221.34194.
10.1016/j.cnsns.2009.02.013
Web of Science® Google Scholar

All articles

Exponential Stability and Periodicity of Fuzzy Delayed Reaction-Diffusion Cellular Neural Networks with Impulsive Effect

Abstract

1. Introduction

2. Preliminaries

3. Main Results and Proofs

4. Numerical Examples

5. Conclusions

Acknowledgments

References

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Exponential Stability and Periodicity of Fuzzy Delayed Reaction-Diffusion Cellular Neural Networks with Impulsive Effect

Abstract

1. Introduction

2. Preliminaries

3. Main Results and Proofs

4. Numerical Examples

5. Conclusions

Acknowledgments

References

Figures

References

Related

Information